Simulado UNICAMP - 2016 Cinemática Vetorial

Simulado UNICAMP - 2016
Cinemática Vetorial
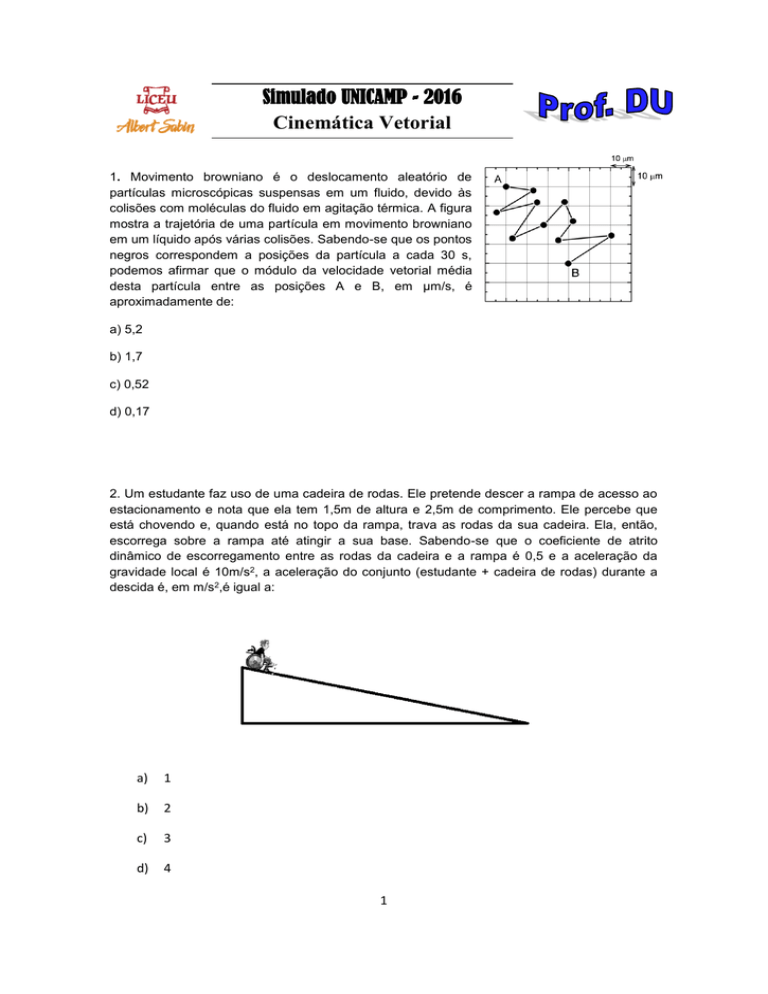
1. Movimento browniano é o deslocamento aleatório de
partículas microscópicas suspensas em um fluido, devido às
colisões com moléculas do fluido em agitação térmica. A figura
mostra a trajetória de uma partícula em movimento browniano
em um líquido após várias colisões. Sabendo-se que os pontos
negros correspondem a posições da partícula a cada 30 s,
podemos afirmar que o módulo da velocidade vetorial média
desta partícula entre as posições A e B, em µm/s, é
aproximadamente de:
a) 5,2
b) 1,7
c) 0,52
d) 0,17
2. Um estudante faz uso de uma cadeira de rodas. Ele pretende descer a rampa de acesso ao
estacionamento e nota que ela tem 1,5m de altura e 2,5m de comprimento. Ele percebe que
está chovendo e, quando está no topo da rampa, trava as rodas da sua cadeira. Ela, então,
escorrega sobre a rampa até atingir a sua base. Sabendo-se que o coeficiente de atrito
dinâmico de escorregamento entre as rodas da cadeira e a rampa é 0,5 e a aceleração da
gravidade local é 10m/s2, a aceleração do conjunto (estudante + cadeira de rodas) durante a
descida é, em m/s2,é igual a:
a)
1
b)
2
c)
3
d)
4
1
3. O cantor Michael Jackson, quando cantou a música Moon Walker, fez um passo de dança
que o permitiu andar para trás. Pelo princípio da dinâmica de Isaac Newton, a causa do
movimento é a força, esta, uma grandeza vetorial.
Desta forma, assinale a opção abaixo que melhor representa as forças que agiram no pé do
cantor no momento em que realizava o passo de andar para trás no palco.
Fonte: http://www.youtube.com/watch?v=XcY4S4OCKFQ
a)
b)
c)
d)
4. Um engenheiro foi convidado por um empresário,
dono de um parque de diversões, a construir um
brinquedo, no qual um motociclista possa pilotar sua
motocicleta em um grande cilindro oco e transparente.
O cilindro será colocado na posição vertical a uma
altura de 5,0 metros em relação ao solo e o motociclista
dará voltas horizontais, naturalmente com toda
segurança. A figura ao lado mostra o cilindro e o
motociclista com sua motocicleta. Considere a
aceleração da gravidade constante e igual g,  o
coeficiente de atrito entre o pneu e a superfície do
cilindro, e o sistema motociclista e motocicleta como um
ponto material de massa m. Assinale a expressão da
velocidade mínima de segurança para o movimento
considerado no texto.
2
a) v 
b) v 
c) v 
R.g

R.
g
 .g
R
d) v  R.g
GABARITO:
Questão 1: D
Observando e aplicando o Teorema de Pitágoras no triângulo
retângulo da figura, obtemos que o módulo do vetor
deslocamento é de 50µm. Portanto:

50
 r


v 
v 
 v  0,17 m / s
t
10 .30
Questão 2: B
De acordo com a figura , temos as forças que interagem no corpo e as medidas da rampa,
portanto:
PX – Fat = m.a
m.g.senθ - µ.m.g.cosθ = m.a
a = g(senθ - µ.cosθ)
a = 10 ( 0,6 – 0,5.0,8)
a = 2,0 m/s²
Questão 3: A
3
Questão 4: A
De acordo com as forças que agem no corpo temos que:
Fat = P
µ.N = m.g
v2
.m.  m.g  v 
R
4
R.g
