Do que trata a Estatística Estatística Básica (Anova, TH, Regressão

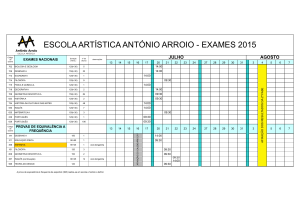
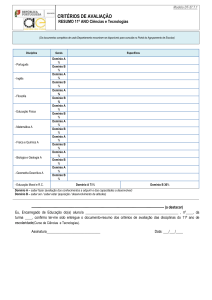
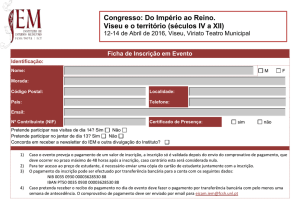
1-Estatística
Descritiva
Do que trata a Estatística
A essência da ciência é a observação.
Estatística: A ciência que se preocupa com a organização, descrição, análise e
interpretação dos dados experimentais. Ramo da Matemática Aplicada. A
palavra estatística provêm de Status.
Curiosidade: Em 1662, John Graunt
publicou os primeiros informes estatísticos.
Era sobre nascimento e mortes.
Estatística Básica (Anova,
TH, Regressão)
Simulação / PO
Séries Temporais
DOE /Taguchi /RSM
Data Mining
Análise de Sistema de Medição
Six Sigma
Estatística Multivariada
Redes Neurais
Amostragem / Pesquisa
Controle de Qualidade
Confiabilidade
Pedro Paulo Balestrassi www.iem.efei.br/pedro 35-3629-1161
1
1-Estatística
Descritiva
População e Amostra
v A População (ou Distribuição) é a coleção de todas as
observações potenciais sobre determinado fenômeno.
v O conjunto de dados efetivamente observados, ou
extraídos, constitui uma Amostra da população.
vUm Censo é uma coleção de dados relativos a Todos os
elementos de uma população.
vUm Parâmetro está para a População assim como uma
Estatística está para a Amostra.
Pedro Paulo Balestrassi www.iem.efei.br/pedro 35-3629-1161
2
1-Estatística
Descritiva
Tipos de Dados
(Também Dados Categóricos
ou de Atributos)
Nominal
Qualitativa
Ordinal
Variável
Discreta
Quantitativa
Contínua
Ex.: Para uma população de peças produzidas em um
determinado processo, poderíamos ter:
Variável
Tipo
Estado: Perfeita ou defeituosa
Qualitativa Nominal
(Variáveis)
Qualidade: 1a, 2a ou 3a categoria Qualitativa Ordinal
No de peças defeituosas
Quantitativa Discreta
Diâmetro das peças
Quantitativa Contínua
Pedro Paulo Balestrassi www.iem.efei.br/pedro 35-3629-1161
3
1-Estatística
Descritiva
<Calc> <Random Data> Números Aleatórios
Aplicação: Gere sequências de valores aleatórios que represente
problemas em sua área.
O que significa o procedimento <Calc> <Set Base>?
Amostragem: Gere a sequência 1 2 3 ...100.
<Calc> <Make Patterned Data>
Selecione uma amostra com 10 valores a partir das sequências geradas
anteriormente.
Use <Calc> Random Data> <Sample from Column>
Pedro Paulo Balestrassi www.iem.efei.br/pedro 35-3629-1161
4
1-Estatística
Descritiva
<Graphical Summary>
Ex.:Número de acessos à página do Site da Empresa
durante os últimos 100 dias úteis.
Aplicação:
Gere uma sequência de
dados que represente um
processo em sua área e
calcule as estatísticas
desse conjunto de dados.
Use:
<Random> e
<Display Descriptive
Statistics>
Pedro Paulo Balestrassi www.iem.efei.br/pedro 35-3629-1161
5
1-Estatística
Descritiva
Medidas de Posição: Média
n
Aritmética Simples
x=
x1 + x 2 ++...+
L+ xn
n
=
∑x
i =1
i
n
n
Aritmética Ponderada
x1 p1 + x2 p2 ++...+
L + x n pn
x=
=
p1 + p2 ++...+
L + pn
∑xp
i =1
n
i
i
∑p
i =1
i
Um pouco sobre arredondamento de médias:
q Tome uma decimal acima da dos dados: Ex.: 2,4 3,4 e 5,7 => média =3,73
q Em várias operações, arredonde apenas o resultado final
Pedro Paulo Balestrassi www.iem.efei.br/pedro 35-3629-1161
6
1-Estatística
Descritiva
Um Cidadão Americano “Médio”
q Chama-se Robert
q Pesa 78 Kg
q Manequim 48
q 85 cm de cintura
q Consome anualmente 8,5 Kg massa, 11,8Kg de bananas, 1,8 Kg de
batatas fritas, 8,15Kg de sorvete e 35,8 Kg de carne.
q Vê TV por ano 2567 horas
q Recebe anualmente 585 “coisas” por correio (cartas e outros)
q Diariamente dorme 7,7 horas, gasta 21 minutos para chegar ao trabalho e
trabalha 6,1 horas
Pedro Paulo Balestrassi www.iem.efei.br/pedro 35-3629-1161
7
1-Estatística
Descritiva
Medidas de Posição: Mediana
Se n é ímpar:
 n + 1
~
 termo
x =
 2 
o
Ex.:
Se n é par:
o
o
n 
n

  termo +  + 1 termo
2 
2

~
x=
2
{35, 36, 37, 38, 40, 40, 41, 43 ,46} ⇒ ~x = 40
15 + 16
~
{12 , 14, 14 ,15, 16, 16,17 , 20} ⇒ x = 2 = 15,5
Mediana é o valor “do meio” de um conjunto de dados dispostos em
ordem crescente ou decrescente.
Inconveniente: Não considera todos os valores da amostra!
Pedro Paulo Balestrassi www.iem.efei.br/pedro 35-3629-1161
8
1-Estatística
Descritiva
Ex.:
Média x Mediana
{ 200, 250, 250, 300, 450, 460, 510 }
x = 345,7
~
x = 300
Ambas são boas medidas
de Tendência Central.
Prefira a média
{ 200, 250, 250, 300, 450, 460, 2300 }
x
= 601
~
x = 300
Devido ao Outlier
2300, a mediana é
melhor estatística que
a média.
Pedro Paulo Balestrassi www.iem.efei.br/pedro 35-3629-1161
9
1-Estatística
Descritiva
Medidas de Dispersão
Rode e Entenda o
programa Interativo da
PQ Systems
Discuta:
1) Porque os bancos adotam fila única?
2) “Por favor, com quantos dias de antecedência eu
devo postar uma carta de aniversário para minha
mãe?”
Pedro Paulo Balestrassi www.iem.efei.br/pedro 35-3629-1161
10
1-Estatística
Descritiva
Variabilidade
A = { 3, 4, 5, 6, 7 }
B = { 1, 3, 5, 7, 9 }
C = { 5, 5, 5, 5 }
D = { 3, 5, 5, 7 }
E = { 3.5, 5, 6.5 }
Uma medida de Posição não é
suficiente para descrever um conjunto
de dados. Os Conjuntos ao lado
mostram isso! Eles possuem mesma
média, sendo diferentes.
Algumas medidas de Variabilidade:
Amplitude (H): Tem o inconveniente de levar em conta apenas os
dois valores extremos:
HÁ =7-3=4
Amplitude=Range
Pedro Paulo Balestrassi www.iem.efei.br/pedro 35-3629-1161
11
1-Estatística
Descritiva
Medidas de Dispersão
Considerando os desvios em relação à média, temos, para A, por
exemplo:
xi - x
{-2, -1, 0, 1, 2}
A = { 3, 4, 5, 6, 7 }
n
∑ (x
Inconveniente:
i =1
1
n
n
i =1
i =1
− x ) = ∑ x1 − ∑ x = n x − n x ≡ 0
Uma opção para analisar os desvios das observações é:
considerar o total dos quadrados dos desvios.
∑ (x
5
i =1
− x ) =4 + 1 + 0 + 1 + 4 = 10
2
i
Pedro Paulo Balestrassi www.iem.efei.br/pedro 35-3629-1161
12
1-Estatística
Descritiva
Desvio Padrão
Associando ao número de elementos da amostra (n), tem-se:
.
∑ (x
n
S2
=
S = S2
i =1
i
− x)
2
...que é a Variância ( Var(x))
n
...que é o Desvio Padrão (DP(x)), uma
medida que é expressa na mesma unidade
dos dados originais
Pedro Paulo Balestrassi www.iem.efei.br/pedro 35-3629-1161
13
1-Estatística
Descritiva
Dispersão: Fórmulas Alternativas
∑ (x
n
n
S =
2
∑ (x
i =1
i
n
− x)
n
2
=
∑x
i =1
n
2
S =
2
i
−x
2
Variância Populacional
(σ2 ou σn 2 )
Pedro Paulo Balestrassi www.iem.efei.br/pedro 35-3629-1161
i =1
i
− x)
2
n−1
Variância
Amostral
n-1 está
Relacionado a
um problema de
tendenciosidade
14
1-Estatística
Descritiva
Exemplo
Calcular a Variância e o Desvio Padrão de X
X
X
5
4
3
1
2
Uma Regra
Prática para
conjunto de dados
típicos:
S=Amplitude/4
Média
Média==33
X
=
Soma dos pontos de dados
(X − X )
(X − X )
2
1
0
-2
-1
4
1
0
4
1
2
Número dos pontos de dados
S= S
2
Raiz
RaizQadrada
Qadrada
da
daVariância
Variância
==Desv.Pa.
Desv.Pa.==SS
==1,58
1,58
S2
Soma
Somada
da
última
últimacoluna
coluna
==10
10
Divide
DivideaaSoma
Soma
por
por(n-1):
(n-1):
2
==Variância
Variância==SS2
==2,5
2,5
Pedro Paulo Balestrassi www.iem.efei.br/pedro 35-3629-1161
15
1-Estatística
Descritiva
Expressões para Média e Variância
N
µ =
Média da População
∑X
i =1
i
N
N
Desvio Padrão da População
σ =
2
(X
−
µ
)
∑ i
i=1
N
n
x=
Média da Amostra
xi
∑
i=1
n
N
Desvio Padrão da Amostra
s=
2
(X
X
)
−
∑ i
i=1
Pedro Paulo Balestrassi www.iem.efei.br/pedro 35-3629-1161
n -1
16
1-Estatística
Descritiva
Outlier ( fora da distância do Q3 + 1,5D )
Observação Máxima
75%
109
Q3=75ª Percentil
104
DBP
*
Outra Estratégia: Percentis e Boxplot
50%
99
D=Q3-Q1
94
25%
Interquartil
Q2=Mediana (50ª Percentil)
Q1=25ª Percentil
EDA (Exploratory
Data Analysis) e
Método dos Cinco
Números
Boxplot é desgastante quando feito sem
computador pois supõe a ordenação de dados.
Pedro Paulo Balestrassi www.iem.efei.br/pedro 35-3629-1161
17
1-Estatística
Descritiva
Percentis e Boxplot
Use Boxplot.mtw e faça o
Graphical Summary
çValor do meio
(n+1)/4 0
2.(n+1)/4
Quartis:
0
è Q1=Quarta Observação Crescente=71.7
è Q3=Quarta Observação Decrescente=150.6
3.(n+1)/4 0
Para valores
não inteiros
dos quartis,
usa-se
interpolação
Outliers: Q3+1.5D=150.6+1.5(150.6-71.7)=268.95
è São outliers valores maiores que 268.95
Pedro Paulo Balestrassi www.iem.efei.br/pedro 35-3629-1161
18
1-Estatística
Descritiva
Percentis e Boxplot
Exercício: <StatGame><Describing Data><BoxPlot>
Pedro Paulo Balestrassi www.iem.efei.br/pedro 35-3629-1161
19
1-Estatística
Descritiva
Boxplot – Stack Columns
Exercício: Como conduzir uma análise de questionário
(com escala de Likert) usando Boxplot?
Use:
<Graph> <Boxplot>
Use a opção <Frame>
<Multiple Graph>
Likert.mtw
Entenda o
procedimento de
empilhamento de
colunas (Stack):
Avaliacao
100
50
<Manip>
<Stack Columns>
0
Perg1
Perg2
Perg3
Perg4
Perg5
Perg6
Perguntas
Pedro Paulo Balestrassi www.iem.efei.br/pedro 35-3629-1161
20
1-Estatística
Descritiva
xi − x
zi =
s
Escores padronizados (z)
xi - x considera o afastamento de xi em relação à média.
A divisão por s torna s como unidade ou padrão de medida.
Ex.: Dois grupos de pessoas acusam os seguintes dados:
Nesses grupos há duas
Grupo Peso médio Desvio Padrão
pessoas que pesam
A
66.5 kg
6.38 kg
respectivamente, 81.2 kg e
B
72.9 kg
7.75 kg
88.0 kg.
81,2 − 66,5
88 − 72,9
em A : z A =
= 2,3 e em B : z B =
= 1,95
6,38
7,75
Logo, a pessoa de A revela um maior excesso relativo de peso.
Pedro Paulo Balestrassi www.iem.efei.br/pedro 35-3629-1161
21
1-Estatística
Descritiva
Regra 68 -- 95 -- 99
Escores padronizados (z)
Regra 68 -- 95 -- 99
xi − x
zi =
s
ü Cerca de 68% dos valores estão a menos de 1 desvio padrão a
contar da média (-1 < z < 1)
ü Cerca de 95% dos valores estão a menos de 2 desvios padrão a
contar da média (-2 < z < 2)
ü Cerca de 99% dos valores estão a menos de 3 desvios padrão a
contar da média (-3 < z < 3)
Pedro Paulo Balestrassi www.iem.efei.br/pedro 35-3629-1161
22
1-Estatística
Descritiva
Distribuição de Freqüências
Ex.: População = X=Diâmetro de determinada peça (em mm).
Dados brutos: { 168, 164, 164, 163, 165, 168, 165, 164, 168, 168 }
Rol: { 163, 164, 164, 164, 165, 165, 168, 168, 168, 168 }
Amplitude (H) = 168 - 163 = 5
∑n
K
ni
fi
Ni
Fi
X
(Frequência
Absoluta)
(Frequência
Relativa)
(Frequência
Absoluta
Acumulada)
Frequência
Relativa
Acumulada)
163
1
0.1
1
0.1
164
3
0.3
4
0.4
165
2
0.2
6
0.6
168
4
0.4
10
1.0
Σ
10
1
Pedro Paulo Balestrassi www.iem.efei.br/pedro 35-3629-1161
i
=n
1
ni
fi =
n
K
∑f
i=1
i
=1
Ni
Fi =
n
23
1-Estatística
Descritiva
Classes (ou Categorias)
x
xi
ni
fi
f%
(Variável)
(ponto
médio)
(frequência
absoluta)
(frequência
relativa)
(frequência
percentual)
Ni
Fi
(Absoluta (Relativa
Acum.)
Acum.)
F%
(Percentual
Acum.)
10
20
15
2
0.04
4
2
0.04
4
20
30
25
12
0.24
24
14
0.28
28
30
40
35
18
0.36
36
32
0.64
64
40
50
45
13
0.26
26
45
0.9
90
50
60
55
5
0.1
10
50
1.0
100
50
1
100
Σ
Pedro Paulo Balestrassi www.iem.efei.br/pedro 35-3629-1161
24
1-Estatística
Descritiva
Histogramas
Construção da tabela de distribuição de
freqüências a partir do histograma de classes
desiguais.
Exercício: Complete a tabela.
ni
X
10
fi
|-- 20
8
10
6
20 |-- 30
4
ni
30 |-- 40
2
40 |-- 60
10
20
30
40
60
x
Σ
Pedro Paulo Balestrassi www.iem.efei.br/pedro 35-3629-1161
1
25
1-Estatística
Descritiva
Ramo-e-folhas
 x
Ramos  x x
Folhas
 x x x x x
 x x x
Ex.:
11
81
113
108
74
79
78
90
93
105
109
93
106
103
100
100
100
101
101
101
95
90
94
90
91
92
93
87
89
78
89
85
94
86
3
10
8
5
9
6
3
0
0
0
1 1
1
9
0
3
3
5
0
4
0
1
2 3
4
8
1
7
9
9
5
6
7
4
9
8
8
11
3
10+
8
5
9
6
10-
3
0
0
0
1
1
1
9-
0
3
3
5
0
4
0
8
1
7
9
9
5
6
7
4
9
8
8
Pedro Paulo Balestrassi www.iem.efei.br/pedro 35-3629-1161
1
2
3
4
26
1-Estatística
Descritiva
Ramo-e-folhas
Obtenha o
seguinte Folha
e Ramo na
planilha
grafico.mtw
Compare os
resultados
fazendo um
Histograma.
O que
representa tal
coluna?
Stem-and-Leaf Display:
folha_ramo
Stem-and-leaf of Ramo
Leaf Unit = 1.0
1
4
5
10
(10)
13
12
5
1
7
7
8
8
9
9
10
10
11
N = 33
4
889
Coluna
1
folha_ramo
56799
0001233344
5
0001113
5689
3
Pedro Paulo Balestrassi www.iem.efei.br/pedro 35-3629-1161
27
1-Estatística
Descritiva
Plot
Exercício no Minitab: Faça o gráfico
abaixo a partir da planilha grafico.mtw
Pedro Paulo Balestrassi www.iem.efei.br/pedro 35-3629-1161
28
1-Estatística
Descritiva
<Marginal Plot>
Faça o gráfico abaixo a
partir da planilha
grafico.mtw
Pedro Paulo Balestrassi www.iem.efei.br/pedro 35-3629-1161
29
1-Estatística
Descritiva
Runchart
Abra runchart.mtw
<Stat> <Quality Tools>
<Run Chart>
•Column=Tempo na fila
•Subgroup Size=1
v
Os dados representam uma série temporal
v
Tal gráfico é útil para ver a estabilidade de
um processo.
v
Control Chart é Melhor!
Pedro Paulo Balestrassi www.iem.efei.br/pedro 35-3629-1161
30
1-Estatística
Descritiva
Multi-Vari
•Identifica Diversos tipos de variação
•A análise de efeitos é similar em DOE
•Permite identificar interações
•Não é o mesmo que Estatística Multivariada
Use
TempoSinter
0,5
Sinter.mtw
23,5
<Stat>
22,5
<Quality Tools>
21,5
1,0
Força
2,0
<Multi-Vari>:
20,5
Response: Força
19,5
Factor1: TempoSinter
18,5
Factor2: TipoMetal
17,5
15
18
21
TipoMetal
Pedro Paulo Balestrassi www.iem.efei.br/pedro 35-3629-1161
31
1-Estatística
Descritiva
S
cv =
x
Coeficiente de Variação (cv)
cv exprime a variabilidade em termos relativos. É uma medida
adimensional e sua grande utilidade é permitir a comparação
das variabilidades em diferentes conjuntos de dados.
Ex.: Testes de resistência à tração aplicados a dois tipos diferentes de aço:
Média (kg/mm2) s (kg/mm2)
Tipo I 27,45
2,0
Tipo II 147,00
17,25
2
cvI =
= 7,29 %
27 ,45
17,25
cv II =
= 11,73 %
147
Assim, apesar do Tipo I ser menos resistente, é ele mais estável, mais consistente. O
uso do coeficiente de variação pode ser pensado considerando a questão: Um desvio
padrão de 10 se a média é 10.000 é bem diferente se a média é 100!
Pedro Paulo Balestrassi www.iem.efei.br/pedro 35-3629-1161
32
1-Estatística
Descritiva
Skewness and Kurtosis
Assimetria (Skewness)
Próximo de 0: Simétrico
Menor que 0: Assimétrico à
Esquerda
Maior que 0: Assimétrico à
Direita
Achatamento (Kurtosis)
Próximo de 0: Pico Normal
Menor que 0: Mais achatada
que o Normal (Uniforme)
Maior que 0: Menos achatada
que o normal (Afinada)
Pedro Paulo Balestrassi www.iem.efei.br/pedro 35-3629-1161
33
1-Estatística
Descritiva
Estudar é preciso!
• Livro Texto: Montgomery/Runger
– Capítulo 1: Ler
– Capítulo 2: Resolver todos os
exercícios em que o uso de computador
é indicado. Os arquivos de dados do
Minitab podem ser obtidos na página
www.iem.efei.br/pedro.
Pedro Paulo Balestrassi www.iem.efei.br/pedro 35-3629-1161
34