testes 6ª série ensino fundamental

PROFESSOR: Raphael Carvalho
BANCO DE QUESTÕES - FÍSICA - 2ª SÉRIE - ENSINO MÉDIO
==============================================================================================
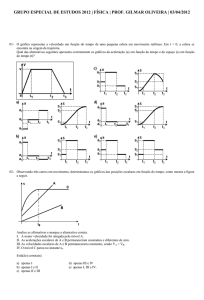
01- O transporte fluvial de cargas é pouco explorado no Brasil, considerando-se nosso vasto conjunto de rios navegáveis.
Uma embarcação navega a uma velocidade de 26 nós, medida em relação à água do rio (use 1 nó = 0,5 m/s). A
correnteza do rio, por sua vez, tem velocidade aproximadamente constante de 5,0 m/s em relação às margens.
 Qual é o tempo aproximado de viagem entre duas cidades separadas por uma extensão de 40 km de rio, se o barco
navega rio acima, ou seja, contra a correnteza?
(A) 2 horas e 13 minutos.
(C) 51 minutos.
(B) 1 hora e 23 minutos.
(D) 37 minutos.
02- Em um trecho retilíneo de estrada, dois veículos, A e B, mantêm velocidades constantes VA  14 m/s e VB  54 km/h
 Sobre os movimentos desses veículos, pode-se afirmar que:
(A) ambos apresentam a mesma velocidade escalar.
(B) mantidas essas velocidades, A não conseguirá ultrapassar B.
(C) A está mais rápido do que B.
(D) a cada segundo que passa, A fica dois metros mais distante de B.
(E) depois de 40 s A terá ultrapassado B.
03- Em uma manhã de calmaria, um Veículo Lançador de Satélite (VLS) é lançado verticalmente do solo e, após um
período de aceleração, ao atingir a altura de 100 m, sua velocidade linear é constante e de módulo igual a 20,0 m/s.
Alguns segundos após atingir essa altura, um de seus conjuntos de instrumentos desprende-se e move-se livremente
sob ação da força gravitacional. A figura fornece o gráfico da velocidade vertical, em m/s, do conjunto de instrumentos
desprendido como função do tempo, em segundos, medido no intervalo entre o momento em que ele atinge a altura de
100 m até o instante em que, ao retornar, toca o solo.
a) Determine a ordenada y do gráfico no instante t = 0 s e a altura em que o conjunto de instrumentos se desprende do
VLS.
b) Calcule, através dos dados fornecidos pelo gráfico, a aceleração gravitacional do local e, considerando
determine o instante no qual o conjunto de instrumentos toca o solo ao retornar.
Página 1 de 10 - 03/08/2012 - 7:40
2  1,4 ,
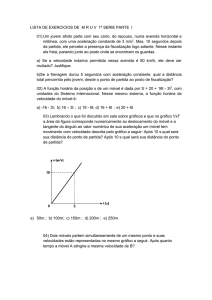
04- Um jogador de futebol chuta uma bola a 30 m do gol adversário. A bola descreve uma trajetória parabólica, passa por
cima da trave e cai a uma distância de 40 m de sua posição original.
 Se, ao cruzar a linha do gol, a bola estava a 3 m do chão, a altura máxima por ela alcançada esteve entre:
(A) 4,1 e 4,4 m.
(C) 3,2 e 3,5 m.
(B) 3,8 e 4,1 m.
(D) 3,5 e 3,8 m.
05- Policiais rodoviários são avisados de que um carro B vem trafegando em alta velocidade numa estrada. No instante t 0
em que o carro B passa, os policiais saem em sua perseguição. A figura ilustra as velocidades do carro B e do carro
dos policiais (P) em função do tempo.
 Assinale a alternativa que especifica o instante de tempo em que o carro P alcança o carro B.
(A) t1
(B) t 2
(C) t 3
(D) t 4
(E) t 5
06- Uma partícula se afasta de um ponto de referência O, a partir de uma posição inicial A, no instante t = 0 s, deslocandose em movimento retilíneo e uniforme, sempre no mesmo sentido.
A distância da partícula em relação ao ponto O, no instante t = 3,0 s, é igual a 28,0 m e, no instante t = 8,0 s, é igual a
58,0 m.
 Determine a distância, em metros, da posição inicial A em relação ao ponto de referência O.
07- Um avião vai decolar em uma pista retilínea. Ele inicia seu movimento na cabeceira da pista com velocidade nula e
2
corre por ela com aceleração média de 2,0 m/s até o instante em que levanta voo, com uma velocidade de 80 m/s,
antes de terminar a pista.
a) Calcule quanto tempo o avião permanece na pista desde o início do movimento até o instante em que levanta voo.
b) Determine o menor comprimento possível dessa pista.
Página 2 de 10 - 03/08/2012 - 7:40
08- Duas partículas, A e B, que executam movimentos retilíneos uniformemente variados, se encontram em t = 0 na mesma
posição. Suas velocidades, a partir desse instante, são representadas pelo gráfico abaixo.
2
As acelerações experimentadas por A e B têm o mesmo módulo de 0,2m s .
 Com base nesses dados, é correto afirmar que essas partículas se encontrarão novamente no instante:
(A) 10 s.
(C) 100 s.
(B) 50 s.
(D) 500 s.
09- Em um local onde g  10m / s2 , um objeto é lançado verticalmente para cima, a partir do solo terrestre. O efeito do ar é
desprezível.
O objeto atinge 20% de sua altura máxima com uma velocidade de módulo igual a 40 m/s.
 A altura máxima atingida pelo objeto vale:
(A) 200 m.
(C) 100 m.
(B) 150 m.
(D) 75 m.
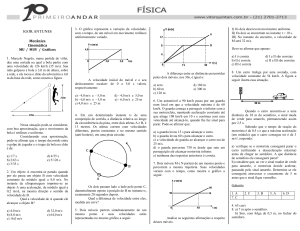
10- Num jogo de vôlei, uma atacante acerta uma cortada na bola no instante em que a bola está parada numa altura h
acima do solo. Devido à ação da atacante, a bola parte com velocidade inicial V 0, com componentes horizontal e
vertical, respectivamente em módulo, Vx = 8 m/s e Vy = 3 m/s, como mostram as figuras 1 e 2.
Após a cortada, a bola percorre uma distância horizontal de 4 m, tocando o chão no ponto P.
 Considerando que durante seu movimento a bola ficou sujeita apenas à força gravitacional e adotando g = 10 m/s , a
altura h, em m, onde ela foi atingida é:
2
(A) 2,25.
(C) 2,75.
(E) 3,25.
Página 3 de 10 - 03/08/2012 - 7:40
(B) 2,50.
(D) 3,00.
11- O gráfico abaixo indica a posição (S) em função do tempo (t) para um automóvel em movimento num trecho horizontal e
retilíneo de uma rodovia.
 Da análise do gráfico, pode-se afirmar que o automóvel:
(A)
(B)
(C)
(D)
(E)
está em repouso, no instante 1 min.
possui velocidade escalar nula, entre os instantes 3 min e 8 min.
sofreu deslocamento de 4 km, entre os instantes 0 min e 3 min.
descreve movimento progressivo, entre os instantes 1 min e 10 min.
tem a sua posição inicial coincidente com a origem da trajetória.
12- Dois automóveis, M e N, inicialmente a 50 km de distância um do outro, deslocam-se com velocidades constantes na
mesma direção e em sentidos opostos. O valor da velocidade de M, em relação a um ponto fixo da estrada, é igual a 60
km/h. Após 30 minutos, os automóveis cruzam uma mesma linha da estrada.
 Em relação a um ponto fixo da estrada, a velocidade de N tem o seguinte valor, em quilômetros por hora:
(A) 40.
(C) 60.
(B) 50.
(D) 70.
13- Um corpo de massa 2,0 kg parte do repouso e desce um plano inclinado sem atrito, a partir de seu topo. O ângulo
dessa inclinação com a horizontal é 30° e seu comprimento é 10 m.
 O tempo, em segundos, para esse corpo chegar à base do plano é:
(A) 1.
(C) 3.
(B) 2.
(D) 4.
14- Uma bola é atirada verticalmente para cima em t = 0, com uma certa velocidade inicial.
 Desprezando a resistência do ar e considerando que a aceleração da gravidade é constante, dos gráficos a seguir,
aquele que representa CORRETAMENTE a variação do módulo V da velocidade da bola com o tempo t é:
(A)
(B)
(C)
(D)
Página 4 de 10 - 03/08/2012 - 7:40
15- Uma pessoa lança uma pedra do alto de um edifício com velocidade inicial de 60 m/s e formando um ângulo de 30º com
a horizontal, como mostrado na figura abaixo. Se a altura do edifício é 80 m, qual será o alcance máximo (xf) da pedra,
2
isto é, em que posição horizontal ela atingirá o solo? (dados: sen 30º = 0,5, cos 30º = 0,8 e g = 10 m/s ).
(A) 153 m.
(C) 450 m.
(B) 96 m.
(D) 384 m.
Gabarito
01- (B)
Dados: vA = 5 m/s; vB = 26 nós; 1 nó = 0,5 m/s; d = 40 km.
O módulo da velocidade do barco é:
vB  26  0,5  13 m / s.
Se o barco navega rio acima, a velocidade resultante tem módulo igual à diferença dos módulos:
v  vB  v A  13  5  v  8 m / s  8  3,6  km / h 
v  28,8 km / h.
Aplicando a definição de velocidade escalar:
d
d
40
40
 t  
h  t 
 60min  83,33min 
t
v 28,8
28,8
t  1 h e 23min.
v
02- (B)
Dados: VA = 14 m/s; VB = 54 km/h = 15 m/s.
Como a velocidade de A é menor que a de B, A não conseguirá ultrapassar B.
03- a) O enunciado afirma que após atingir a altura de 100 m a velocidade torna-se constante e igual a 20 m/s. Ora, de 0 a
2 s, a ordenada y mantém-se constante. Então:
y  v0  20 m / s.
O conjunto de instrumentos desprende-se do VLS no instante que sua velocidade começa a diminuir, quando ele fica
apenas sujeito à ação da gravidade, isto é, em t = 2 s. Calculando a área sob a linha do gráfico, encontramos a
altura percorrida de 0 a 2 s. Então, a altura h em que o ocorre o desprendimento é:
h  100  20  2  h  140 m.
A aceleração gravitacional do local é igual ao módulo da aceleração escalar do movimento do conjunto de
instrumentos após o desprendimento.
a
v 0  20

 10 m / s2  g  a  10 m / s2.
t
42
b) A altura máxima (H) atingida pelo conjunto ocorre no instante t = 4 s, instante em que a velocidade se anula.
Calculando a área sob a linha do gráfico de 2 s a 4 s, obtemos a altura percorrida  h  durante a subida livre.
H  h  h  140 
20(2)
2
Página 5 de 10 - 03/08/2012 - 7:40
 H  160 m.
A partir dessa altura, o conjunto entra em queda livre. Então:
H
1 2
g t queda
2
2
 160  5 tqueda
 tqueda  32  4 2  tqueda  5,6 s.
Como a queda livre iniciou-se no instante t = 4 s, o instante t em que o conjunto de instrumentos toca o solo é:
t  4  tqueda  4  5,6  t  9,6 s.
04- (B)
OBS: Essa questão foi cobrada na prova de Matemática, mas admite solução através de conceitos Físicos, aliás,
solução bem mais simples e curta. Serão dadas aqui as duas soluções.
1ª Solução (Matemática):
Encontremos, primeiramente, a equação da parábola que passa pelos pontos dados:
A equação reduzida da parábola de raízes x1 e x2 é: y  a  x  x1  x  x2 .
Nesse caso temos: x1 = 0 e x2 = 40.
Substituindo esses valores na equação dada:
y  a  x  0  x  40   y  ax2  40ax.
Para x = 30  y = 3. Então:
3  a  30   40a  30   3  900a  1200a  a  
2
1
.
100
Assim, a equação da parábola mostrada é:
y
x2
x2
2
 1 
 40 
x  y
 x.

100
100 5
 100 
Para x = 20  h = H. Então:
H
 20 
2
100
H  4 m.

2
 20   H  4  8 
5
2ª Solução (Física):
Pela regra de Galileu, sabemos que, para qualquer movimento uniformemente variado (M.U.V.) com velocidade inicial
nula, os espaços percorridos em intervalos de tempo (t) iguais e subsequentes, as distâncias percorridas são: d, 3d,
5d, 7d...
Ora, a queda livre e o lançamento horizontal na direção vertical são movimentos uniformemente variados a partir do
repouso, valendo, portanto a regra de Galileu. Assim, se a distância de queda num intervalo de tempo inicial (t) é h,
nos intervalos iguais e subsequentes as distâncias percorridas na queda serão: 3h, 5h, 7h...
O lançamento oblíquo, a partir do ponto mais alto (A), pode ser considerando um lançamento horizontal. Como a
componente horizontal da velocidade inicial se mantém constante (vx = v0x), os intervalos de tempo de A até B e de B
até C são iguais, pois as distâncias horizontais são iguais (10 m).
Página 6 de 10 - 03/08/2012 - 7:40
Assim, se de A até B a bola cai h, de B até C ela cai 3h, como ilustrado na figura.
Então:
3h  3  h  1 m.
Mas : H  3h  h  3  1  H  4 m.
3ª Solução (Física):
Como as distâncias horizontais percorridas entre A e B e entre B e C são iguais, os intervalos de tempo entre esses
pontos também são iguais, pois a componente horizontal da velocidade se mantém constante (vx = v0x). Assim, se o
tempo de A até B é t, de A até C é 2t.
Equacionando a distância vertical percorrida na queda de A até B e de A até C, temos:

g 2
A  B : h  2 t


 A  C : H  g  2t 2

2

g 
 H  4  t2 
2 
 H  4h.
Mas, da Figura: H  h  3  4h  h  3  h  1 m.
Como H  4h  H  4 m.
05- (D)
Considerando que os carros B e P iniciem seus movimentos no mesmo espaço e no mesmo instante t 0 (instante em
que o carro B passa pelos policiais e a perseguição se inicia), eles irão se encontrar novamente quando percorrerem o
mesmo deslocamento no mesmo intervalo de tempo, ou seja: SB  SP e tB  tP .
Conseguiremos encontrar o deslocamento de cada carro através da área do gráfico, já que o gráfico dado é de
velocidade em função do tempo.
Página 7 de 10 - 03/08/2012 - 7:40
Analisando o gráfico dado, concluímos que as áreas serão iguais em t4:
06- t1 = 3 s  S1 = 28 m; t2 = 8 s  S2 = 58 m.
Calculando a velocidade:
v
S 58  28 30


 v  6 m/s.
t
83
5
Calculando a posição inicial A (no instante t = 0):
v
28  SA
S
 6
 28  SA  18  SA = 28 – 18  SA = 10 m
t
30
07- Da definição de aceleração escalar média:
am 
v
t

t 
v 80  0

am
2

t  40 s.
Da equação de Torricelli:
v 2  v 02  2 am S

S 
802
4

S  1.600 m.
A pista deve ter comprimento mínimo igual à distância percorrida pelo avião na decolagem. Assim, D = 1.600 m.
08- (D)
2
2
Dados: v0A = 50 m/s; v0B = -50 m/s; aA = -0,2 m/s (reta decrescente); aB = 0,2 m/s (reta crescente).
Adotando origem no ponto de partida e lembrando que a equação horária do espaço no MUV é S  S0  v 0 t 
temos:
SA  50 t  0,1 t 2

2
SB  50 t  0,1 t
No encontro, SA = SB:
50 t  0,1 t 2  50 t  0,1 t 2
t  0 (não convém)
t
100
0,2
 t  500 s.
Página 8 de 10 - 03/08/2012 - 7:40
 100 t  0,2 t 2  0  t 100  0,2 t   0 
1 2
at ,
2
09- (C)
A figura mostra o movimento do corpo:
Aplicando Torricelli, vem:
V2  V02  2aΔS  0  402  2x10x0,8H  16H  1600  H  100m .
10- (C)
Na direção horizontal (x) o movimento é uniforme. Assim, podemos calcular o tempo (t) que a bola leva para tocar o
chão.
vx 
x
t

t
x 4

vx 8

t  0,5 s.
Na direção vertical (y) o movimento é uniformemente variado, com aceleração igual à da gravidade (g).
g t2
2
h  2,75 m.
h  v oy t 

h  3  0,5  
10  0,5 
2
2
 1,5  1,25 
11- (B)
Note que entre 3 e 8 min a posição não varia. Portanto, o carro está parado.
12- (A)
Seja P o ponto de encontro desses dois automóveis, como indicado na figura.
Do instante mostrado até o encontro, que ocorreu no ponto P, passaram-se 30 min ou 0,5 h, a distância percorrida pelo
automóvel M é:
DM = vM t = 60 (0,5) = 30 km.
Nesse mesmo intervalo de tempo, o automóvel N percorreu, então:
DN = 50 – 20 = 30 km.
Assim:
Página 9 de 10 - 03/08/2012 - 7:40
vN =
DN 20
 vN = 40 km/h.

t 0,5
13- (B)
Dados: m = 2 kg;  = 30°; S = 10 m; v0 = 0.
Como o movimento é retilíneo, a resultante é paralela à velocidade:
R = PX  m a  m g sen  a = g sen 30° = 10 (0,5) a = 5 m/s .
2
Da função horária do espaço:
S = v0 t +
a t2
5t 2
2
 10 =
 t = 4  t = 2 s.
2
2
14- (A)
O lançamento vertical, livre de resistência do ar, é um movimento uniformemente variado. A velocidade varia com o
tempo de acordo com a função: v = v0  g t.
Portanto, o gráfico é uma reta, sendo o módulo da velocidade decrescente na subida, crescente na descida e nulo no
ponto mais alto.
15- (D)
As componentes horizontal e vertical da velocidade inicial são:
v 0x  v 0 cos 0  v 0 cos30  60  0,8  48 m / s.


v 0y  v 0 sen0  v 0 sen30  60  0,5  30 m / s.
Adotando referencial no solo e orientando a trajetória para cima temos:
2
y0 = 80 m; v0y = 30 m/s e g = -10 m/s .
Desprezando os efeitos do ar, a equação do movimento no eixo y é:
y  y0  v 0y t 
1 2
at
2

y  80  30 t  5 t 2.
Quando a pedra atinge o solo, y = 0. Substituindo:
0  80  30 t  5 t 2 
t
t 2  6 t  16  0

t
6  36  4 116 
2

6  10 t  8 s.

2
t  2 s (não convém).
No eixo x o movimento é uniforme. A equação é:
x  x0  v 0x t

x  0  48 8 

x  384 m.
FM/1206/BANCO DE QUESTOES/FISICA/FISICA - 2a SERIE - ENSINO MEDIO - 2a ETAPA - 2012–RAPHAEL CARVALHO.DOC
Página 10 de 10 - 03/08/2012 - 7:40