Trabalho - Webnode

Trabalho
Parte I
1. (Uerj 2014) Um chuveiro elétrico com resistência igual a
5Ω é conectado a uma rede elétrica que fornece 120 V de
tensão eficaz.
Determine a energia elétrica, em kWh, consumida pelo
chuveiro durante 10 minutos.
2. (Fuvest 2014) Um contêiner com equipamentos
científicos é mantido em uma estação de pesquisa na
Antártida. Ele é feito com material de boa isolação térmica
e é possível, com um pequeno aquecedor elétrico, manter
sua temperatura interna constante, Ti = 20°C, quando a
temperatura externa é Te = −40°C. As paredes, o piso e o
teto do contêiner têm a mesma espessura, ε = 26 cm, e
são de um mesmo material, de condutividade térmica
k = 0,05 J / (s ⋅ m ⋅ °C). Suas dimensões internas são
2 × 3 × 4 m3 . Para essas condições, determine
a) a área A da superfície interna total do contêiner;
b) a potência P do aquecedor, considerando ser ele a única
fonte de calor;
c) a energia E, em kWh, consumida pelo aquecedor em um
dia.
Note e adote:
A quantidade de calor por unidade de tempo (Φ) que
flui através de um material de área A, espessura ε  e
condutividade térmica k, com diferença de
temperatura ΔT entre as faces do material, é dada
por: Φ = kAΔT / ε.
3. (Fuvest 2014) No sistema cardiovascular de um ser
humano, o coração funciona como uma bomba, com
potência média de 10 W, responsável pela circulação
sanguínea. Se uma pessoa fizer uma dieta alimentar de
2500 kcal diárias, a porcentagem dessa energia utilizada
para manter sua circulação sanguínea será,
aproximadamente, igual a
a) A sonda atingiu o repouso, na superfície de Marte, 7
minutos após a sua entrada na atmosfera. Calcule o
módulo da força resultante média de desaceleração da
sonda durante sua descida.
b) Considere que, após a entrada na atmosfera a uma
altitude h0 = 125 km, a força de atrito reduziu a
velocidade da sonda para v = 4000 m/s quando a altitude
atingiu h =100 km. A partir da variação da energia
mecânica, calcule o trabalho realizado pela força de
atrito neste trecho. Considere a aceleração da gravidade
de Marte, neste trecho, constante e igual a gMarte = 4
2
m/s .
5. (Uerj 2013) Uma pessoa adulta, para realizar suas
atividades rotineiras, consome em média, 2500 kcal de
energia por dia.
Calcule a potência média, em watts, consumida em um dia
por essa pessoa para realizar suas atividades.
Utilize: 1 cal = 4,2 J.
6. (Fgv 2013) A montadora de determinado veículo
produzido no Brasil apregoa que a potência do motor que
equipa o carro é de 100 HP (1HP ≅ 750W ) . Em uma pista
horizontal e retilínea de provas, esse veículo, partindo do
repouso, atingiu a velocidade de 144 km/h em 20 s.
Sabendo que a massa do carro é de 1 000 kg, o rendimento
desse motor, nessas condições expostas, é próximo de
a) 30%.
b) 38%.
c) 45%.
d) 48%.
e) 53%.
7. (Uftm 2012) No resgate dos mineiros do Chile, em 2010,
foi utilizada uma cápsula para o transporte vertical de cada
um dos enclausurados na mina de 700 metros de
profundidade. Considere um resgate semelhante ao feito
naquele país, porém a 60 metros de profundidade, tendo a
cápsula e cada resgatado um peso total de 5 × 104 N. O
cabo que sustenta a cápsula não pode suportar uma força
que exceda 7,5 × 104 N. Adote g = 10 m s2 para o local
do resgate. Esse movimento tem aceleração máxima no
primeiro trecho e, a seguir, movimento retardado, com o
motor desligado, até o final de cada ascensão.
Note e adote:
1 cal = 4 J.
a) 1%
b) 4%
c) 9%
d) 20%
e) 25%
4. (Unicamp 2013) Em agosto de 2012, a NASA anunciou o
pouso da sonda Curiosity na superfície de Marte. A sonda,
de massa m = 1000 kg, entrou na atmosfera marciana a
uma velocidade v0 = 6000 m/s.
www.soexatas.com
Página 1
a) Qual deve ter sido o menor tempo para cada ascensão
do elevador?
b) Calcule a potência máxima que o motor deve ter
desenvolvido em cada resgate.
8. (Uerj 2012) Uma pessoa empurrou um carro por uma
distância de 26 m, aplicando uma força F de mesma direção
e sentido do deslocamento desse carro. O gráfico abaixo
representa a variação da intensidade de F, em newtons, em
função do deslocamento d, em metros.
Desprezando o atrito, o trabalho total, em joules, realizado
por F, equivale a:
a) 117
b) 130
c) 143
d) 156
9. (Uftm 2012) Um motor ideal é usado para acionar uma
bomba de rendimento igual a 40%, cuja função é elevar 300
litros de água por minuto a uma altura de 20 m. Esse
motor consome óleo combustível de poder calorífico igual a
4,0 × 107 J kg. Considerando g = 10 m s2 e
dágua = 1,0 kg L, responda:
a) Qual é a potência efetiva do motor utilizado nessa
tarefa?
b) Qual foi o consumo de óleo, em kg, utilizado pelo motor,
em uma hora de trabalho?
10. (Espcex (Aman) 2012) Uma força constante F de
intensidade 25 N atua sobre um bloco e faz com que ele
sofra um deslocamento horizontal. A direção da força
forma um ângulo de 60° com a direção do deslocamento.
Desprezando todos os atritos, a força faz o bloco percorrer
uma distância de 20 m em 5 s.
A potência desenvolvida pela força é de:
Dados: Sen 60° = 0,87; Cos 60º = 0,50.
a) 87 W
b) 50 W
www.soexatas.com
c) 37 W
d) 13 W
e) 10 W
11. (G1 - cps 2012) A hidroponia consiste em um método
de plantio fora do solo em que as plantas recebem seus
nutrientes de uma solução, que flui em canaletas, e é
absorvida pelas raízes.
Por meio de uma bomba hidráulica, em determinada horta
hidropônica, a solução é elevada até uma altura de 80 cm,
sendo vertida na canaleta onde estão presas as mudas.
Devido a uma ligeira inclinação da canaleta, a solução se
move para o outro extremo, lá sendo recolhida e
direcionada ao reservatório do qual a bomba reimpulsiona
o líquido, como mostra a figura.
Dados:
– Aceleração da gravidade: g = 10 m s2
– 1 kg de água equivale a 1 litro de água
Trabalho
– Potência =
intervalo de tempo
– Trabalho = massa × gravidade × altura
Suponha que nessa horta hidropônica foi empregada uma
bomba com potência de 20 W. Se toda a potência dessa
bomba pudesse ser empregada para elevar a água até a
canaleta, a cada um segundo (1 s ) , o volume de água que
fluiria seria, em litros,
a) 2,0.
b) 2,5.
c) 3,0.
d) 3,5.
e) 4,0.
12. (Fuvest 2012)
Um pequeno cata-vento do tipo Savonius, como o
esquematizado na figura ao lado, acoplado a uma bomba
d'água, é utilizado em uma propriedade rural. A potência
útil P (W) desse sistema para bombeamento de água pode
Página 2
2
ser obtida pela expressão P = 0,1⋅ A ⋅ v 3 , em que A (m ) é
a área total das pás do cata-vento e v (m/s), a velocidade
do vento. Considerando um cata-vento com área total das
2
pás de 2 m , velocidade do vento de 5 m/s e a água sendo
elevada de 7,5 m na vertical, calcule
a) a potência útil P do sistema;
b) a energia E necessária para elevar 1 L de água;
c) o volume V1 de água bombeado por segundo;
d) o volume V2 de água, bombeado por segundo, se a
velocidade do vento cair pela metade.
15. (Uerj 2011) Um homem arrasta uma cadeira sobre um
piso plano, percorrendo em linha reta uma distância de 1
m. Durante todo o percurso, a força que ele exerce sobre a
cadeira possui intensidade igual a 4 N e direção de 60° em
relação ao piso.
O gráfico que melhor representa o trabalho T, realizado por
essa força ao longo de todo o deslocamento d, está
indicado em:
NOTE E ADOTE
3
Densidade da água = 1 g/cm .
2
Aceleração da gravidade g = 10 m/s .
13. (Unicamp 2012) O óleo lubrificante tem a função de
reduzir o atrito entre as partes em movimento no interior
do motor e auxiliar na sua refrigeração. O nível de óleo no
cárter varia com a temperatura do motor, pois a densidade
do óleo muda com a temperatura. A tabela abaixo
apresenta a densidade de certo tipo de óleo para várias
temperaturas.
T (ºC)
0
20
40
60
80
100
120
140
ρ (kg/litro)
0,900
0,882
0,876
0,864
0,852
0,840
0,829
0,817
a) Se forem colocados 4 litros de óleo a 20ºC no motor de
um carro, qual será o volume ocupado pelo óleo quando
o motor estiver a 100ºC?
b) A força de atrito que um cilindro de motor exerce sobre
o pistão que se desloca em seu interior tem módulo
Fatrito = 3,0 N . A cada ciclo o pistão desloca-se 6,0 cm
para frente e 6,0 cm para trás, num movimento de vai e
vem. Se a frequência do movimento do pistão é de 2500
ciclos por minuto, qual é a potência média dissipada pelo
atrito?
14. (Espcex (Aman) 2011) Um bloco, puxado por meio de
uma corda inextensível e de massa desprezível, desliza
sobre uma superfície horizontal com atrito, descrevendo
um movimento retilíneo e uniforme. A corda faz um ângulo
de 53° com a horizontal e a tração que ela transmite ao
bloco é de 80 N. Se o bloco sofrer um deslocamento de 20
m ao longo da superfície, o trabalho realizado pela tração
no bloco será de:
(Dados: sen 53° = 0,8 e cos 53° = 0,6)
a) 480 J
b) 640 J
c) 960 J
d) 1280 J
e) 1600 J
www.soexatas.com
a)
b)
c)
d)
16. (Unesp 2011) A quantidade de energia informada na
embalagem de uma barra de chocolate é igual a 200 kcal.
Após o consumo dessa barra, uma pessoa decide eliminar a
energia adquirida praticando uma corrida, em percurso
plano e retilíneo, com velocidade constante de 1,5 m/s, o
que resulta em uma taxa de dissipação de energia de 500
W. Considerando 1 kcal = 4200 J , quantos quilômetros,
aproximadamente, a pessoa precisará correr para dissipar a
mesma quantidade de calorias ingeridas ao comer o
chocolate?
17. (Ifsp 2011) Um atleta de 80 kg massa, durante uma
prova de atletismo, percorre 100 m rasos durante um
intervalo de tempo de 9,0 segundos, cruzando a linha de
chegada com uma velocidade escalar de 43,2 km/h.
Adotando que 1 cal = 4 joules e desconsiderando os efeitos
de resistência do ar, podemos afirmar que a energia gasta,
Página 3
por segundo, pelas forças musculares do atleta, em
calorias, é de
a) 160.
b) 240.
c) 360.
d) 640.
e) 720.
18. (G1 - col.naval 2011) De acordo com a lei da
conservação da energia, a energia não pode ser criada nem
destruída, podendo apenas ser transformada de uma forma
em outra. Baseado nesse princípio, algumas equipes de
fórmula 1 usaram, durante a temporada de 2009, um
Sistema de Recuperação da Energia Cinética (em inglês
KERS)que proporcionava uma potência extra ao carro de
cerca de 80 CV durante 6 segundos, melhorando assim as
ultrapassagens. Essa energia era acumulada durante as
frenagens usando parte da energia cinética do carro, que
seria dissipada pelos freios em forma de calor.
Se toda a energia acumulada pelo KERS pudesse ser
integralmente utilizada por um elevador para erguer uma
carga total de 1000 kg, qual seria, aproximadamente, a
altura máxima atingida por esse elevador, desprezando-se
todos os atritos envolvidos?
Dados: 1 CV = 735 W
2
g = 10 m/s
a) 20m
b) 25m
c) 30m
d) 35m
e) 40m
19. (Fgv 2010) Contando que ao término da prova os
vestibulandos da GV estivessem loucos por um docinho, o
vendedor de churros levou seu carrinho até o local de saída
dos candidatos. Para chegar lá, percorreu 800 m, metade
sobre solo horizontal e a outra metade em uma ladeira de
inclinação constante, sempre aplicando sobre o carrinho
uma força de intensidade 30 N, paralela ao plano da
superfície sobre a qual se deslocava e na direção do
movimento. Levando em conta o esforço aplicado pelo
vendedor sobre o carrinho, considerando todo o traslado,
pode-se dizer que,
a) na primeira metade do trajeto, o trabalho exercido foi de
12 kJ, enquanto que, na segunda metade, o trabalho foi
maior.
b) na primeira metade do trajeto, o trabalho exercido foi de
52 kJ, enquanto que, na segunda metade, o trabalho foi
menor.
c) na primeira metade do trajeto, o trabalho exercido foi
nulo, assumindo, na segunda metade, o valor de 12 kJ.
d) tanto na primeira metade do trajeto como na segunda
metade, o trabalho foi de mesma intensidade,
totalizando 24 kJ.
e) o trabalho total foi nulo, porque o carrinho parte de um
estado de repouso e termina o movimento na mesma
condição.
www.soexatas.com
20. (Ufla 2010) Uma partícula de massa m está sujeita a
uma força resultante que gera uma potência constante P.
Considerando que, para t0 = 0, a partícula está parada (v0 =
0), é correto afirmar que a expressão da sua velocidade em
função do tempo é dada por:
 2P 
a) V = 
⋅t
m
m
b) V = 
⋅t
 2P 
2
m
c) V = 
⋅ t2

 2P 
1
 2P  2 21
d) V = 
 ⋅t
m
21. (Unesp 2009) Suponha que os tratores 1 e 2 da figura
arrastem toras de mesma massa pelas rampas
correspondentes, elevando-as à mesma altura h. Sabe-se
que ambos se movimentam com velocidades constantes e
que o comprimento da rampa 2 é o dobro do comprimento
da rampa 1.
Chamando de τ1 e τ 2 os trabalhos realizados pela força
gravitacional sobre essas toras, pode-se afirmar que:
a) τ1 = 2τ2 ; τ1 > 0 e τ 2 < 0.
b) τ1 = 2τ2 ; τ1 < 0 e τ 2 > 0.
c) τ1 = τ2 ; τ1 < 0 e τ 2 < 0.
d) 2τ1 = τ 2 ; τ1 > 0 e τ 2 > 0.
e) 2τ1 = τ2 ; τ1 < 0 e τ 2 < 0.
22. (Pucrj 2008) Durante a aula de educação física, ao
realizar um exercício, um aluno levanta verticalmente um
peso com sua mão, mantendo, durante o movimento, a
velocidade constante.
Pode-se afirmar que o trabalho realizado pelo aluno é:
a) positivo, pois a força exercida pelo aluno atua na mesma
direção e sentido oposto ao do movimento do peso.
b) positivo, pois a força exercida pelo aluno atua na mesma
direção e sentido do movimento do peso.
c) zero, uma vez que o movimento tem velocidade
constante.
d) negativo, pois a força exercida pelo aluno atua na mesma
direção e sentido oposto ao do movimento do peso.
e) negativo, pois a força exercida pelo aluno atua na mesma
direção e sentido do movimento do peso.
23. (G1 - cps 2008) A pesca é um dos lazeres mais
procurados. Apetrechos e equipamentos utilizados devem
ser da melhor qualidade. O fio para pesca é um exemplo.
Ele deve resistir à força que o peixe faz para tentar
Página 4
permanecer na água e também ao peso do peixe. Supondo
que o peixe seja retirado, perpendicularmente em relação à
superfície da água, com uma força constante, o trabalho
a) será resistente, considerando apenas a força peso do
peixe.
b) da força resultante será resistente, pois o peixe será
retirado da água.
c) será indiferente, pois a força, sendo constante, implicará
em aceleração igual a zero.
d) poderá ser resistente em relação à força que o pescador
aplicará para erguer o peixe.
e) de qualquer força aplicada no peixe será nulo, pois força
e deslocamento são perpendiculares entre si.
24. (Unesp 2008) O teste Margaria de corrida em escada é
um meio rápido de medida de potência anaeróbica de uma
pessoa. Consiste em fazê-la subir uma escada de dois em
dois degraus, cada um com 18 cm de altura, partindo com
velocidade máxima e constante de uma distância de alguns
0
metros da escada. Quando pisa no 8 . degrau, a pessoa
0
aciona um cronômetro, que se desliga quando pisa no 12 .
degrau. Se o intervalo de tempo registrado para uma
pessoa de 70 kg foi de 2,8 s e considerando a aceleração da
2
gravidade igual a 10 m/s , a potência média avaliada por
este método foi de
a) 180 W.
b) 220 W.
c) 432 W.
d) 500 W.
e) 644 W.
25. (Unesp 2007) A relação entre calor e outras formas de
energia foi objeto de intensos estudos durante a Revolução
Industrial, e uma experiência realizada por James P. Joule
foi imortalizada. Com ela, ficou demonstrado que o
trabalho mecânico e o calor são duas formas diferentes de
energia e que o trabalho mecânico poderia ser convertido
em energia térmica. A figura apresenta uma versão
atualizada da máquina de Joule. Um corpo de massa 2 kg é
suspenso por um fio cuidadosamente enrolado em um
carretel, ligado ao eixo de um gerador.
transferidos para a água 24 J de energia térmica. Sabendo
que esse valor corresponde a 80% da energia mecânica, de
qual altura em relação ao solo o corpo foi abandonado?
2
Adote g = 10 m/s .
Parte II
TEXTO PARA AS PRÓXIMAS 2 QUESTÕES:
Dados:
Aceleração da gravidade: g = 10 m/s2
Densidade da água: ρa = 1,0 g/cm3 = 1000 kg/m3
Velocidade da luz no vácuo: c = 3,0 ⋅ 108 m/s
Pressão atmosférica: Patm = 1,0 ⋅ 105 N/m2
1 litro = 1 dm3 = 10−3 m3
1 ano - luz = 9,461⋅ 1015 m
Calor específico da água: c a = 1 cal/gºC = 4000 J/KgºC
1 eV = 1,6 ⋅ 1019 J
1 cal = 4,2 J
1. (Ufjf 2011) Um sistema de polia móvel, como mostrado
na figura abaixo, pode ser muito útil para suspender algum
objeto utilizando uma força menor que o peso do próprio
objeto. Considere a corda sem massa e inextensível e
despreze as massas das polias e qualquer perda de energia
do sistema.
a) Considerando que o peso foi deslocado a uma altura h,
qual o trabalho realizado pela força P ?
b) Qual o deslocamento total da extremidade A e qual o
trabalho realizado pela força F ?
c) Qual o valor da força F para um sistema formado por N
polias móveis? Justifique sua resposta.
O gerador converte a energia mecânica do corpo em
elétrica e alimenta um resistor imerso em um recipiente
com água. Suponha que, até que o corpo chegue ao solo,
depois de abandonado a partir do repouso, sejam
www.soexatas.com
2. (Ufjf 2011) A usina hidrelétrica de Itaipu é formada por
20 unidades geradoras, que fornecem 19% da energia
elétrica consumida no Brasil. Em cada uma das tubulações
das unidades geradoras, passam 600 m3 de água por
segundo, sob ação da gravidade, que fazem girar a turbina
Página 5
e o gerador. A eficiência no processo de geração de energia
elétrica é da ordem de 75%.
a) Se a altura da coluna d'água entre o ponto mais baixo e o
ponto mais alto da tubulação é de aproximadamente
roximadamente h =
120 m,, calcule a potência elétrica gerada na usina.
b) Calcule a energia fornecida pela usina durante um dia.
3. (Ufjf 2010) Em uma construção civil, os operários usam
algumas máquinas simples para facilitar e diminuir sua
carga diária de energia gasta na execução de seu trabalho.
Uma das máquinas simples mais utilizadas são, por
exemplo, as roldanas fixas e móveis. Em um dia comum
co
de
trabalho, um operário deve elevar, com velocidade
constante, um bloco de pedra de massa m =100
100 kg para o
segundo andar da obra, que fica a uma altura h = 5,0 m em
relação ao solo. Para essa tarefa, o operário utilizou um
sistema com duas roldanas, uma
ma fixa e outra móvel, e um
cabo de massa desprezível, como mostra a figura.
2
Considere g = 10m/s .
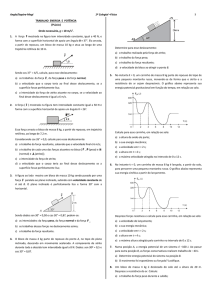
Sabendo que a criança de 36 kg parte do repouso,
de uma altura de 6,0 m acima da base do toboágua,
colocado à beira de uma piscina, calcule:
Dado: g = 10,0 m/s
2
a) A força normal, na horizontal, exercida sobre a criança
pela parede lateral do toboágua,
toboágua no ponto indicado na
figura (curva do toboágua situada a 2,0 m da sua base)
onde o raio de curvatura é igual a 80 cm.
b) A força dissipativa média exercida pela água da piscina,
necessária para fazer a criança parar ao atingir 1,5 m de
profundidade, considerando que a criança entra na água
da piscina com velocidade, na vertical,
aproximadamente igual a 10,9 m/s, desprezando-se,
desprezando
neste cálculo, a perda de energia mecânica no impacto
da criança com a água da piscina.
a) Faça um diagrama de forças que atuam sobre o bloco e
identifique cada uma das forças.
b) Calcule a tração no cabo que está em contato com a mão
do operário
rário e o trabalho realizado por ele, para elevar o
bloco até o segundo andar da obra.
c) Se foi gasto um tempo t =10 s para o operário elevar o
bloco até o segundo andar da obra, calcule a potência
gasta nessa tarefa.
Parte III
1. (Unifesp 2010) Um dos brinquedos prediletos de
crianças no verão é o toboágua.. A emoção do brinquedo
está associada à grande velocidade atingida durante a
descida, uma vez que o atrito pode ser desprezado devido à
presença da água em todo o percurso do brinquedo, bem
como
o à existência das curvas fechadas na horizontal, de
forma que a criança percorra esses trechos encostada na
parede lateral (vertical) do toboágua.
www.soexatas.com
2. (Unifesp 2007) Uma das alternativas modernas para a
geração de energia elétrica limpa e relativamente barata é
a energia eólica. Para a avaliação preliminar da potência
eólica de um gerador situado em um determinado local, é
necessário calcular a energia cinética do vento que
atravessa a área varrida pelas hélices desse gerador por
unidade de tempo.
a) Faça esse cálculo para obter a potência média disponível,
em watts, de um gerador
erador eólico com hélices de 2,0 m de
comprimento, colocado em um lugar onde, em média, a
velocidade do vento, perpendicular à área varrida pelas
2
hélices, é de 10 m/s. Dados: área do círculo: A = πr
3
(adote π = 3,1); densidade do ar: d(ar) = 1,2 kg/m .
b) Mesmo em lugares onde o vento é abundante, há
momentos de calmaria ou em que sua velocidade não é
suficiente para mover as pás do gerador. Indique uma
Página 6
forma para se manter o fornecimento de energia elétrica
aos consumidores nessas ocasiões.
3. (Unifesp 2006) A figura representa o gráfico do módulo F
de uma força que atua sobre um corpo em função do seu
deslocamento x. Sabe-se que a força atua sempre na
mesma direção e sentido do deslocamento.
a) Qual o consumo médio de calorias desse atleta, sabendo
que o tempo dessa prova é de cerca de 0,50h?
Dado: 1 cal = 4,2 J.
b) Admita que a velocidade do atleta é constante. Qual a
intensidade média da força exercida sobre o atleta durante
a corrida?
6. (Unifesp 2002) O pequeno bloco representado na figura
desce o plano inclinado com velocidade constante.
Pode-se afirmar que o trabalho dessa força no trecho
representado pelo gráfico é, em joules,
a) 0.
b) 2,5.
c) 5,0.
d) 7,5.
e) 10.
4. (Unifesp 2006) Após algumas informações sobre o carro,
saímos em direção ao trecho off-road. Na primeira
acelerada já deu para perceber a força do modelo. De
acordo com números do fabricante, são 299 cavalos de
potência [...] e os 100 km/h iniciais são conquistados em
satisfatórios 7,5 segundos, graças à boa relação
peso/potência, já que o carro vem com vários componentes
de alumínio.
(http://carsale.uol.com.br/opapoecarro/testes/ava
l_050404discovery.shtml 5)
O texto descreve um teste de avaliação de um veículo
importado, lançado neste ano no mercado brasileiro.
Sabendo que a massa desse carro é de 2 400 kg, e
admitindo 1 cv = 740 W e 100 km/h = 28 m/s, pode-se
afirmar que, para atingir os 100 km/h iniciais, a potência
útil média desenvolvida durante o teste, em relação à
potência total do carro, foi, aproximadamente de
(Sugestão: efetue os cálculos utilizando apenas dois
algarismos significativos.)
a) 90%.
b) 75%.
c) 60%.
d) 45%.
e) 30%.
5. (Unifesp 2005) Avalia-se que um atleta de 60kg, numa
prova de 10000m rasos, desenvolve uma potência média de
300W.
www.soexatas.com
Isso nos permite concluir que
a) não há atrito entre o bloco e o plano e que o trabalho do
peso do bloco é nulo.
b) há atrito entre o bloco e o plano, mas nem o peso do
bloco nem a força de atrito realizam trabalho sobre o
bloco.
c) há atrito entre o bloco e o plano, mas a soma do trabalho
da força de atrito com o trabalho do peso do bloco é
nula.
d) há atrito entre o bloco e o plano, mas o trabalho da força
de atrito é maior que o trabalho do peso do bloco.
e) não há atrito entre o bloco e o plano; o peso do bloco
realiza trabalho, mas não interfere na velocidade do
bloco.
7. (Unifesp 2002) Avalia-se que uma pessoa sentada,
estudando e escrevendo, consome em média 1,5
quilocalorias por minuto (1,0quilocaloria=4000 joules).
Nessas condições, pode-se afirmar que a potência dissipada
pelo seu organismo, agora, resolvendo esta prova, equivale,
aproximadamente, à potência de
a) um relógio digital, de pulso.
b) uma lâmpada miniatura, de lanterna.
c) uma lâmpada incandescente comum.
d) um ferro elétrico.
e) um chuveiro elétrico.
Parte IV
1. (Unesp 2011) A quantidade de energia informada na
embalagem de uma barra de chocolate é igual a 200 kcal.
Após o consumo dessa barra, uma pessoa decide eliminar a
energia adquirida praticando uma corrida, em percurso
plano e retilíneo, com velocidade constante de 1,5 m/s, o
que resulta em uma taxa de dissipação de energia de 500
Página 7
W. Considerando 1 kcal = 4200 J , quantos quilômetros,
aproximadamente, a pessoa precisará correr para dissipar a
mesma quantidade de calorias ingeridas ao comer o
chocolate?
2. (Unesp 2009) Suponha que os tratores 1 e 2 da figura
arrastem toras de mesma massa pelas rampas
correspondentes, elevando-as à mesma altura h. Sabe-se
que ambos se movimentam com velocidades constantes e
que o comprimento da rampa 2 é o dobro do comprimento
da rampa 1.
Chamando de τ1 e τ 2 os trabalhos realizados pela força
gravitacional sobre essas toras, pode-se afirmar que:
a) τ1 = 2τ2 ; τ1 > 0 e τ 2 < 0.
b) τ1 = 2τ2 ; τ1 < 0 e τ 2 > 0.
c) τ1 = τ2 ; τ1 < 0 e τ 2 < 0.
d) 2τ1 =
e) 2τ1 =
τ2 ; τ1 > 0 e τ2 > 0.
τ2 ; τ1 < 0 e τ2 < 0.
3. (Unesp 2009) Segundo informação da empresa
fabricante, um trator florestal (Trator Florestal de Rodas
545C) é capaz de arrastar toras por meio do seu cabo
5
exercendo sobre elas uma força de módulo 2,0 ⋅ 10 N ,
com velocidade constante de módulo 2,0 m/s. Desprezando
a massa do cabo e supondo que a força por ele exercida
seja horizontal e paralela ao solo, determine a potência útil
desenvolvida pelo trator.
4. (Unesp 2008) O teste Margaria de corrida em escada é
um meio rápido de medida de potência anaeróbica de uma
pessoa. Consiste em fazê-la subir uma escada de dois em
dois degraus, cada um com 18 cm de altura, partindo com
velocidade máxima e constante de uma distância de alguns
0
metros da escada. Quando pisa no 8 . degrau, a pessoa
0
aciona um cronômetro, que se desliga quando pisa no 12 .
degrau. Se o intervalo de tempo registrado para uma
pessoa de 70 kg foi de 2,8 s e considerando a aceleração da
2
gravidade igual a 10 m/s , a potência média avaliada por
este método foi de
a) 180 W.
b) 220 W.
c) 432 W.
d) 500 W.
e) 644 W.
5. (Unesp 2007) Uma técnica secular utilizada para
aproveitamento da água como fonte de energia consiste
em fazer uma roda, conhecida como roda d'água, girar sob
ação da água em uma cascata ou em correntezas de
www.soexatas.com
pequenos riachos. O trabalho realizado para girar a roda é
aproveitado em outras formas de energia. A figura mostra
um projeto com o qual uma pessoa poderia, nos dias atuais,
aproveitar-se do recurso hídrico de um riacho, utilizando
um pequeno gerador e uma roda d'água, para obter
energia elétrica destinada à realização de pequenas tarefas
em seu sítio.
Duas roldanas, uma fixada ao eixo da roda e a outra ao eixo
do gerador, são ligadas por uma correia. O raio da roldana
do gerador é 2,5 cm e o da roldana da roda d'água é R. Para
que o gerador trabalhe com eficiência aceitável, a
velocidade angular de sua roldana deve ser 5 rotações por
segundo, conforme instruções no manual do usuário.
Considerando que a velocidade angular da roda é 1 rotação
por segundo, e que não varia ao acionar o gerador, o valor
do raio R da roldana da roda d'água deve ser
a) 0,5 cm.
b) 2,0 cm.
c) 2,5 cm.
d) 5,0 cm.
e) 12,5 cm.
6. (Unesp 2007) A relação entre calor e outras formas de
energia foi objeto de intensos estudos durante a Revolução
Industrial, e uma experiência realizada por James P. Joule
foi imortalizada. Com ela, ficou demonstrado que o
trabalho mecânico e o calor são duas formas diferentes de
energia e que o trabalho mecânico poderia ser convertido
em energia térmica. A figura apresenta uma versão
atualizada da máquina de Joule. Um corpo de massa 2 kg é
suspenso por um fio cuidadosamente enrolado em um
carretel, ligado ao eixo de um gerador.
O gerador converte a energia mecânica do corpo em
Página 8
elétrica e alimenta um resistor imerso em um recipiente
com água. Suponha que, até que o corpo chegue ao solo,
depois de abandonado a partir do repouso, sejam
transferidos para a água 24 J de energia térmica. Sabendo
que esse valor corresponde a 80% da energia mecânica, de
qual altura em relação ao solo o corpo foi abandonado?
2
Adote g = 10 m/s .
7. (Unesp 2007) Em vários países no mundo, os recursos
hídricos são utilizados como fonte de energia elétrica. O
princípio de funcionamento das hidrelétricas está baseado
no aproveitamento da energia potencial gravitacional da
água, represada por uma barragem, para movimentar
turbinas que convertem essa energia em energia elétrica.
3
Considere que 700 m de água chegam por segundo a uma
turbina situada 120 m abaixo do nível da represa. Se a
3
massa específica da água é 1000 kg/m e considerando g =
2
10 m/s , calcule a potência fornecida pelo fluxo de água.
8. (Unesp 2002) Um projétil de 20 gramas, com velocidade
de 240m/s, atinge o tronco de uma árvore e nele penetra
uma certa distância até parar.
Desprezando o atrito, o trabalho total, em joules, realizado
por F, equivale a:
a) 117
b) 130
c) 143
d) 156
3. (Uerj 2011) Um homem arrasta uma cadeira sobre um
piso plano, percorrendo em linha reta uma distância de 1
m. Durante todo o percurso, a força que ele exerce sobre a
cadeira possui intensidade igual a 4 N e direção de 60° em
relação ao piso.
O gráfico que melhor representa o trabalho T, realizado por
essa força ao longo de todo o deslocamento d, está
indicado em:
a)
a) Determine a energia cinética Ec do projétil antes de
colidir com o tronco e o trabalho T realizado sobre o projétil
na sua trajetória no interior do tronco, até parar.
b) Sabendo que o projétil penetrou 18cm no tronco da
árvore, determine o valor médio Fm da força de resistência
que o tronco ofereceu à penetração do projétil.
b)
Parte V
1. (Uerj 2014) Um chuveiro elétrico com resistência igual a
5Ω é conectado a uma rede elétrica que fornece 120 V de
tensão eficaz.
Determine a energia elétrica, em kWh, consumida pelo
chuveiro durante 10 minutos.
2. (Uerj 2012) Uma pessoa empurrou um carro por uma
distância de 26 m, aplicando uma força F de mesma direção
e sentido do deslocamento desse carro. O gráfico abaixo
representa a variação da intensidade de F, em newtons, em
função do deslocamento d, em metros.
c)
d)
4. (Uerj 2010) Um objeto é deslocado em um plano sob a
ação de uma força de intensidade igual a 5 N, percorrendo
em linha reta uma distância igual a 2 m.
Considere a medida do ângulo entre a força e o
deslocamento do objeto igual a 15º, e T o trabalho
realizado por essa força. Uma expressão que pode ser
utilizada para o cálculo desse trabalho, em joules, é T= 5 x 2
x sen θ .
Nessa expressão, θ equivale, em graus, a:
a) 15
b) 30
www.soexatas.com
Página 9
c) 45
d) 75
5. (Uerj 2006) Observe as situações a seguir, nas quais um
homem desloca uma caixa ao longo de um trajeto AB de 2,5
m.
Parte VI
1. (Fuvest 2014) No sistema cardiovascular de um ser
humano, o coração funciona como uma bomba, com
potência média de 10 W, responsável pela circulação
sanguínea. Se uma pessoa fizer uma dieta alimentar de
2500 kcal diárias, a porcentagem dessa energia utilizada
para manter sua circulação sanguínea será,
aproximadamente, igual a
Note e adote:
1 cal = 4 J.
a) 1%
b) 4%
c) 9%
d) 20%
e) 25%
As forças F1 e F2, exercidas pelo homem nas duas situações,
têm o mesmo módulo igual a 0,4 N e os ângulos entre suas
direções e os respectivos deslocamentos medem è e 2è.
Se k é o trabalho realizado, em joules, por F1, o trabalho
realizado por F2 corresponde a:
a) 2 k
b) k/2
2
c) (k + 1)/2
2
d) 2 k - 1
6. (Uerj 2005) Um produto vendido no supermercado é
recebido em caixas de papelão contendo 16 embalagens de
3
volume igual a 1.312,5 cm cada.
As massas de cada embalagem, do seu conteúdo e da caixa
de papelão são, respectivamente, 10 g, 1.000 g e 100 g.
O produto é entregue por um caminhão, cuja carroceria
está a 1,5 m de altura em relação ao chão, e descarregado
com o auxílio de uma empilhadeira.
2. (Fuvest 2011) Usando um sistema formado por uma
corda e uma roldana, um homem levanta uma caixa de
massa m, aplicando na corda uma força F que forma um
ângulo θ com a direção vertical, como mostra a figura. O
trabalho realizado pela resultante das forças que atuam na
caixa
- peso e força da corda -, quando o centro de massa da
caixa é elevado, com velocidade constante v, desde a altura
ya até a altura yb, é:
a) nulo.
b) F (yb – ya).
c) mg (yb – ya).
d) F cos ( θ ) (yb – ya).
2
e) mg (yb – ya) + mv /2.
a) Calcule a densidade do produto, sabendo que, em cada
3
embalagem, 62,5 cm estão vazios.
b) Considere o descarregamento de uma única caixa que se
encontra sobre o piso da carroceria. Determine o módulo
do trabalho realizado pela força que a base da empilhadeira
faz sobre essa caixa.
www.soexatas.com
3. (Fuvest 2007) Um carro de corrida, de massa M = 800 kg,
percorre uma pista de provas plana, com velocidade
constante V0 = 60 m/s. Nessa situação, observa-se que a
potência desenvolvida pelo motor, P1 = 120 kW, é
praticamente toda utilizada para vencer a resistência do ar
(Situação 1, pista horizontal). Prosseguindo com os testes,
faz-se o carro descer uma ladeira, com o motor desligado,
de forma que mantenha a mesma velocidade V0 e que
enfrente a mesma resistência do ar (Situação 2, inclinação
α). Finalmente, faz-se o carro subir uma ladeira, com a
mesma velocidade V0, sujeito à mesma resistência do ar
(Situação 3, inclinação θ).
Página 10
b) 2600 W
c) 3000 W
d) 4000 W
e) 6000 W
5. (Fuvest 2006) Um elevador de carga, com massa M = 5
000 kg, é suspenso por um cabo na parte externa de um
edifício em construção. Nas condições das questões a
seguir, considere que o motor fornece a potência P = 150
kW.
a) Estime, para a Situação 1, o valor da força de resistência
do ar FR, em Newton, que age sobre o carro no sentido
oposto a seu movimento.
b) Estime, para a Situação 2, o seno do ângulo de inclinação
da ladeira, sen α, para que o carro mantenha a
velocidade V0=60 m/s.
c) Estime, para a Situação 3, a potência P3 do motor, em
kW, para que o carro suba uma ladeira de inclinação
dada por senθ=0,3, mantendo a velocidade V0 = 60 m/s.
NOTE E ADOTE
Potência = Força × Velocidade
Considere, nessas três situações, que apenas a resistência
do ar dissipa energia.
4. (Fuvest 2007) Em um terminal de cargas, uma esteira
rolante é utilizada para transportar caixas iguais, de massa
M = 80 kg, com centros igualmente espaçados de 1 m.
Quando a velocidade da esteira é 1,5 m/s, a potência dos
motores para mantê-la em movimento é P0. Em um trecho
de seu percurso, é necessário planejar uma inclinação para
que a esteira eleve a carga a uma altura de 5 m, como
indicado. Para acrescentar essa rampa e manter a
velocidade da esteira, os motores devem passar a fornecer
uma potência adicional aproximada de
a) Determine a força F1, em N, que o cabo exerce sobre o
elevador, quando ele é puxado com velocidade constante.
b) Determine a força F2, em N, que o cabo exerce sobre o
elevador, no instante em que ele está subindo com uma
2
aceleração para cima de módulo a = 5 m/s .
c) Levando em conta a potência P do motor, determine a
velocidade V2, em m/s, com que o elevador estará subindo,
2
nas condições do item (b) (a = 5 m/s ).
d) Determine a velocidade máxima VL, em m/s, com que o
elevador pode subir quando puxado pelo motor.
NOTE E ADOTE:
A potência P, desenvolvida por uma força F, é igual ao
produto da força pela velocidade V do corpo em que atua,
quando V tem a direção e o sentido da força.
6. (Fuvest 2005) Um sistema mecânico faz com que um
corpo de massa M0, após um certo tempo em queda, atinja
uma velocidade descendente constante V0, devido ao efeito
do movimento de outra massa m, que age como freio. A
massa m é vinculada a uma haste H, presa ao eixo E de um
cilindro C, de raio R0, conforme mostrado na figura a seguir.
Quando a massa M0 cai, desenrola-se um fio que
movimenta o cilindro e o eixo, fazendo com que a massa m
descreva um movimento circular de raio R0. A velocidade V0
é mantida constante, pela força de atrito, entre a massa m
e a parede A, devido ao coeficiente de atrito ì entre elas e à
força centrípeta que age sobre essa massa. Para tal
situação, em função dos parâmetros m, M0, R0, V0, ì e g,
determine:
a) 1200 W
www.soexatas.com
Página 11
da nave imediatamente após o resgate?
b) Qual foi a variação da energia cinética total nesse
resgate?
3. (Unicamp 2003) Um corpo que voa tem seu peso P
equilibrado por uma força de sustentação atuando sobre a
superfície de área A das suas asas. Para voos em baixa
altitude esta força pode ser calculada pela expressão
P/A = 0,37 V
NOTE E ADOTE:
O trabalho dissipado pela força de atrito em uma volta é
igual ao trabalho realizado pela força peso, no movimento
correspondente da massa M0, com velocidade V0.
2
onde V é uma velocidade de voo típica deste corpo. A
relação P/A para um avião de passageiros é igual a 7200
2
N/m e a distância b entre as pontas das asas (envergadura)
é de 60 m. Admita que a razão entre as grandezas P/A e b é
aproximadamente a mesma para pássaros e aviões.
a) o trabalho Tg, realizado pela força da gravidade, quando
a massa M0 percorre uma distância vertical correspondente
a uma volta completa do cilindro C.
b) o trabalho TA, dissipado pela força de atrito, quando a
massa m realiza uma volta completa.
c) a velocidade V0, em função das demais variáveis.
Parte VII
1. (Unicamp 2013) Em agosto de 2012, a NASA anunciou o
pouso da sonda Curiosity na superfície de Marte. A sonda,
de massa m = 1000 kg, entrou na atmosfera marciana a
uma velocidade v0 = 6000 m/s.
a) A sonda atingiu o repouso, na superfície de Marte, 7
minutos após a sua entrada na atmosfera. Calcule o
módulo da força resultante média de desaceleração da
sonda durante sua descida.
b) Considere que, após a entrada na atmosfera a uma
altitude h0 = 125 km, a força de atrito reduziu a
velocidade da sonda para v = 4000 m/s quando a altitude
atingiu h =100 km. A partir da variação da energia
mecânica, calcule o trabalho realizado pela força de
atrito neste trecho. Considere a aceleração da gravidade
de Marte, neste trecho, constante e igual a gMarte = 4
2
m/s .
a) Estime a envergadura de um pardal.
b) Calcule a sua velocidade de voo.
c) Em um experimento verificou-se que o esforço muscular
de um pássaro para voar a 10 m/s acarretava um consumo
de energia de 3,2 J/s. Considerando que 25% deste
consumo é efetivamente convertido em potência mecânica,
calcule a força de resistência oferecida pelo ar durante este
voo.
2. (Unicamp 2005) No episódio II do filme Guerra nas
Estrelas, um personagem mergulha em queda livre, caindo
em uma nave que se deslocava horizontalmente a 100 m/s
com os motores desligados. O personagem resgatado
chegou à nave com uma velocidade de 6 m/s na vertical.
Considere que a massa da nave é de 650 kg, a do
personagem resgatado de 80 kg e a do piloto de 70 kg.
a) Quais as componentes horizontal e vertical da velocidade
www.soexatas.com
Página 12