FÍSICA

FÍSICA
3) Sendo o atrito dinâmico, temos:
CADERNO 5 – CURSO D/E
Fat = d FN
FRENTE 1 – MECÂNICA
200 = d . 400 ⇒
n Módulo 19 – Atrito
1)
d = 0,50
Resposta: 0,50
Calculemos, inicialmente, a intensidade da força de atrito de
destaque entre o bloco e o plano de apoio:
3)
→
P = peso do bloco
→
Fdestaque = e Fn = e mg
Fn = reação normal de apoio
→
Fdestaque = 0,50 . 2,0 . 10,0 (N) ⇒
Fat = força de atrito dinâmica
Fdestaque = 10,0N
a) Como a força motriz (F = 9,0N) tem intensidade menor que
a da força de atrito de destaque (10,0N), o atrito será
estático e, portanto:
a) Como o bloco não tem aceleração na direção vertical,
temos:
→
→ →
→
→
→
→
Fn + P = 0 ⇒ Fn = – P ⇒ .Fn. = .P. = mg
Fat = F = 9,0N
Como o bloco está em movimento, a força de atrito é
dinâmica e sua intensidade é dada por:
Como o bloco permaneceu em repouso, sua aceleração é
nula:
→
b) Como a força motriz (F = 12,0N) tem intensidade maior
que a da força de atrito de destaque (10,0N), o atrito será
dinâmico e, portanto:
Fat = d . FN = d mg
→
→
→
.Fat. = m . a . ⇒ mg = m . a . ⇒
.→
a . = g
b) Sendo a aceleração escalar constante e não nula (de
módulo g), o movimento de freada do bloco é uniformemente variado e, para calcular a distância percorrida
até parar (d), podemos usar a Equação de Torricelli:
Fat = 8,0N
Para obtermos o módulo da aceleração do bloco,
aplicamos a 2.a Lei de Newton:
F – Fat = ma
12,0 – 8,0 = 2,0 . a ⇒
→
A força de atrito é a força resultante que está freando o
bloco e, portanto, de acordo com a 2.a Lei de Newton
(PFD), temos:
a=0
Fat = 0,40 . 2,0 . 10,0 (N) ⇒
→
.Fat. = .Fn. = .P. = mg
V2 = V02 + 2 s
Convencionando como positivo o sentido do movimento,
teremos:
a = 2,0m/s2
Respostas: a) Fat = 9,0N e a = 0
b) Fat = 8,0N e a = 2,0m/s2
→
= – . a . = – g
2)
Quando o bloco parar, teremos: V = 0 e s = d.
Assim:
0 = V02 + 2 ( – g) . d
2gd = V02
⇒
V02
d = –––––
2g
Respostas: a) g
V02
b) ––––
2g
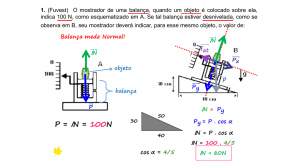
1) Como a aceleração vertical do bloco é nula, temos:
FN = P = mg
FN = 40 . 10 (N) ⇒
FN = 400N
2) Como a aceleração horizontal do bloco é nula, temos:
Fat = F = 200N
4)
A força responsável pela aceleração da caixa é a força de
atrito aplicada pelo plano de apoio:
PFD(caixa): Fat = ma
Se o caminhão acelerar, a caixa tende a escorregar para trás
e a força de atrito é dirigida para frente.
Se o caminhão frear, a caixa tende a escorregar para frente e
a força de atrito é dirigida para trás.
–1
7)
A partir do gráfico, temos:
Fat
destaque
Fat
din
= 1,0N
= 0,8N
Fat
destaque
= E FN = E P
1,0 = E 1,0 ⇒ E = 1,0
Fat
din
Para a caixa não escorregar, o atrito deve ser estático e teremos:
Fat E FN
= D FN = D P
0,8 = D 1,0 ⇒ D = 0,8
Resposta: B
ma E mg
a E g
amáx = E g = 0,60 . 10,0m/s2
8)
a) 1) Força de atrito que o chão aplica em A:
Fat = (PA + PB)
amáx = 6,0m/s2
Fat = 0,50 . 100 (N) ⇒
Resposta: C
5)
Fat = 50N
2) PFD (A + B): F – Fat = (mA + mB) a
1) fat = A PA = 0,20 . 60,0N = 12,0N
125 – 50 = 10 a
2) fat = B PB = 0,30 . 40,0N = 12,0N
a = 7,5 m/s2
A
B
3) PFD (A + B): F – (fat + fat ) = (mA + mB)a
A
b) 1) Força normal que A aplica em B:
B
60,0 – 24,0 = 10,0a
NAB = PB = mBg = 40N
a = 3,6m/s2
2) Força de atrito que A aplica em B:
PFD(B):
4) PFD (B): FAB – fat = mBa
B
= mBa
Fat
= 4,0 . 7,5 (N) = 30N
AB
AB
FAB – 12,0 = 4,0 . 3,6
FAB – 12,0 = 14,4 ⇒
Fat
3) Força resultante que A aplica em B:
FAB = 26,4N
Resposta: A
6)
a) 1) Fat
destaque
2) Fat
din
2
2
FAB
= N2AB + Fat
= E FN = 0,40 . 40,0N = 16,0N
= E FN = 0,20 . 40,0N = 8,0N
FAB = 50 N
b) Como a força motriz aplicada (10,0N) não superou a força
de atrito de destaque (16,0N), a caixa fica em repouso e
teremos: Fat = F = 10,0N
c) Como a força motriz aplicada (20,0N) superou a força de atrito de destaque (16,0N), o atrito será dinâmico e teremos:
Fat = Fat
din
AB
c) Fat
AB
= E NAB
30 = E 40
E = 0,75
= 8,0N
Respostas: a) 7,5 m/s2
PFD: F – Fat = ma
20,0 – 8,0 = 4,0a ⇒ a = 3,0m/s2
9)
b) 50 N
a)
c) 0,75
PFD: fat = M a
d)
fat FN
F = Fat
din
MaMg
= 8,0N
a g ⇒ amáx = g
e)
b)
PFD:
F – Fat = (M + m) a
F = (M + m) g + (M + m) a
F = (M + m) (a + g)
Fmáx = (M + m) (amáx + g)
Fmáx = (M + m) ( g + g)
Respostas: a) Fat
destaque
= 16,0N; Fat
c) 8,0N; 3,0m/s2
e) vide gráfico
2–
din
= 8,0N
b) 10,0N
d) 8,0N
Fmáx = 2 (M + m) g
Respostas: a) g
b) 2 (M + m) g
10) a) Fat = PX = 0,20 . 20,0 (N) = 4,0N
4)
X
Fat = PY = 0,20 . 30,0 (N) = 6,0N
Esfera 1:
O módulo da aceleração da esfera é igual ao da gravidade:
Y
b) PFD (X + Y):
(F1 – F2) – (Fat + Fat ) = (mX + mY) a
X
Y
34,0 – 10,0 = 5,0 . a
a = 4,8m/s2
c) PFD (X):
F1 – (Fat + F
X
) = mX a
YX
40,0 – (4,0 + FYX) = 2,0 . 4,8
→. = g ⇒ h = 1
.a
–– gt21 (1)
1
2
36,0 – FYX = 9,6
FYX = 26,4 N
Respostas:
Esfera 2:
A componente da aceleração paralela ao plano é:
a) 4,0N e 6,0N
b) 4,8m/s2
c) 26,4N
g
a = g sen 30° = ––
2
Logo:
g
→
. a2. = ––
2
n Módulo 20 – Plano Inclinado
1
Para um corpo em um plano inclinado sem atrito, temos:
1
g
1
d = –– . –– . t22 = –– gt22
2
2
4
PFD: Pt = ma
m g sen = ma
a = g sen h
1
sen 30° = –– = –– ⇒ d = 2h
d
2
Os dois blocos, I e II, terão a mesma aceleração a = g sen e
um ficará parado em relação ao outro.
Resposta: A
2)
1
h = –– gt22 (2)
8
Durante a descida do plano inclinado, a aceleração de cada
bloco é g sen 30°; a força resultante em cada bloco é a componente tangencial do respectivo peso e a força de interação
entre os blocos é nula, isto é:
→ →
→
→
f1 = 0 e f2 = 0
Resposta: A
3)
1) PFD: Pt = ma
1
2
⇒ 2h = –– gt 2
4
Comparando-se as equações (1) e (2), obtemos:
t12
1
1
1
= –– ⇒
–– gt12 = –– gt22 ⇒ –––
2
8
t22
4
t1
1
–––
= ––
t2
2
t1
1
Resposta: ––– = ––
t2
2
5)
mg sen = ma
a = g sen a = 10 . 0,80 (m/s2)
a = 8,0m/s2
1) PFD: Pt – Fat = ma
2) VB2 = VA2 + 2 s (MUV)
km
288
VB = 288 ––– = ––– m/s = 80m/s
h
3,6
mg sen – mg cos = ma
a = g(sen – cos )
2) V2 = V20 + 2 s (MUV)
(80)2 = 0 + 2 . 8,0 . s
V2 = 0 + 2g (sen – cos ) L
s = 4,0 . 102m
V = 2gL (sen – cos )
Resposta: 4,0 . 102m
Resposta: C
–3
6)
a) tAB = tBC ⇒ a1 = a2 ⇒ FR = FR
1
2
Pt = Fat – Pt
Fat = 2Pt
P cos = 2 P sen n Módulo 21 – Componentes
da Resultante
1)
No trecho que contém o ponto P, o movimento do automóvel
é circular uniforme e a força resultante é centrípeta (dirigida
de P para M).
Resposta: D
2)
No trecho retilíneo (MRU), a força resultante é nula. Nos tre-
3
= 2 tg = 2 . ––––
3
b) V = V0 + t
VB = 5,0 . 1,0 (SI)
chos circulares, a força resultante é centrípeta.
m
VB = 5,0 –––
s
mV2
Fcp = ––––
R
c)
Sendo R2 R1 = R3 R4 = R5, temos:
F2 F1 = F3 F4 = F5
Resposta: D
3)
A força total de atrito terá uma componente tangencial que vai equilibrar
a força de resistência do ar, pois o
movimento é uniforme e a resultante
tangencial é nula.
2 3
Respostas: a) ––––––
3
A força total de atrito terá uma
componente normal que fará o papel
de resultante centrípeta.
b) 5,0m/s
c) ver gráfico
7)
Resposta: B
4)
mV2
T = Fcp = –––––
R
PFD: F – Pt = m a
F – mg sen = m a
F = m(a + g sen )
F = 50(2,0 + 10 . 0,60) (N)
m V2máx
Tmáx = ––––––––
R
0,5 V2máx
50 = ––––––––
1,0
F = 400N
Resposta: A
8)
a) A força aplicada pelo fio faz o papel de resultante centrípeta.
V2máx = 100
Vmáx = 10m/s
1) Conforme a figura:
6,0
8,0
sen = ––––– = 0,60 e cos = ––––– = 0,80
10,0
10,0
2) Pt = Psen = 50 . 0,60 (N) = 30N
3) Fat = Pn = P cos = 0,40 . 50 . 0,80 (N) = 16N
4) PFD: F – (Pt + Fat) = m a
m V2máx
b) Tmáx = ––––––––
R
0,5 (20)2
50 = ––––––––
Lmín
50 – (30 + 16) = 5,0a
50 – 46 = 5,0a ⇒
Resposta: B
4–
a = 0,80m/s2
Lmín = 4,0m
Respostas: a) Vmáx = 10m/s
b) Lmín = 4,0m
5)
2)
a)
1) Fat = P = mg
mV2
2) FN = Fcp = –––––
R
3) Fat = d FN
mV2
mg = d –––––
R
60
srel
Vrel = ––––––
⇒ 40 – 30 = –––––
t
t
gR
10 . 1,8
d = ––––
= –––––––
V2
36
t = 6,0s
b) Sendo o movimento circular e uniforme, a força resultante
é centrípeta:
Fcp
mV 2
= –––––
R
d = 0,50
Resposta: E
3)
150 . (40)2
F1(predador) = –––––––––– (N) = 4,8 . 10 4N
5,0
60 . (30)2
F2(presa) = –––––––––– (N) = 1,08 . 10 4N
5,0
Respostas: a) 6,0s
b) Predador: 4,8 . 10 4N ou 48kN
Presa: 1,08 . 10 4N ou 10,8kN
Supondo-se desprezível a influência do ar, a força gravitacional
→
(P ) desempenha o papel de resultante centrípeta no movimento circular e uniforme do míssil.
n Módulo 22 – Exercícios de
Força Centrípeta
1)
mV2
Fcp = P ⇒ ––––
R = mg
1) No bloco A:
F = PA = Mg (1)
V=
gR
Sendo g = 10m/s2 e R = 6,4 . 106m, calculemos V:
V=
10 .
6,4 . 106 (m/s)
⇒
m
km
V = 8,0 . 103 –– = 8,0 ––––
s
s
2πR
2πR
b) V = –––– ⇒ T = ––––
T
V
2 . 3 . 6,4 . 106
T = ––––––––––––––––
(s) ⇒ T = 4800s
8,0 . 103
2) No bloco B:
F = FCP = m2R
T = 80min
B
2
R
2π
F = m –––
T
4π2
F = –––– mR (2)
T2
Respostas: a) 8,0km/s
b) 80min
4)
a)
3) Comparando-se (1 ) e (2), obtém-se:
4π2
Mg = ––– . m R
T2
M
4π2R
––– = ––––––
m
gT2
Resposta: A
–5
1) Cálculo do tempo de queda:
y
sy = V0 t + ––– t2 ↓(+)
y
2
6)
FN + P = Fcp
1,6
2,5
25
1,25 = 0 + ––– T2 ⇒ T2 = ––– = –––
2
1,6
16
m V2
FN + m g = –––––
R
T = 1,25s
Quando V diminui, então FN também diminui.
2) Cálculo de V0:
15,0
x
V0 = ––– ⇒ V0 = –––– m/s ⇒
1,25
t
V0 = 12,0m/s
Quando FN = 0, a velocidade V será a mínima possível:
b)
2
m Vmín
mg = ––––––––
R
gR
Vmín = Vmín = 10 . 2,5 (m/s)
Vmín = 5,0m/s
Resposta: B
FG = Fcp
7)
TA – P = Fcp
2
m VS
m g = ––––––
R
m V2
TA = mg + ––––––
R
VS = gR
V2
TA = m g + ––––
R
VS = 1,6 . 1,6 . 106 (m/s)
VS = 1,6 . 103m/s = 1,6km/s
16,0
TA = 1,0 10,0 + ––––– N
1,0
Respostas: a) 12,0m/s
b) 1,6km/s
TA = 26,0N
5)
a)
Resposta: D
→
8)
No ponto mais baixo da trajetória, a resul→
tante entre a força normal do apoio FN e o
→
peso P faz o papel de resultante centrípeta.
F: força aplicada pelo
apoio
→
P: peso do conjunto
FN – P = Fcp
mV 2
FN = mg + –––––
R
b) A velocidade no ponto C será a mínima possível quando a
força de contato com a gaiola se anular e, nesse caso, o
peso fará o papel de resultante centrípeta.
FC = 0 ⇒ P = Fcp
V2
FN = m g + ––––
R
C
mVC2
m g = –––––
R
Dados:
VC =
gR
=
10 . 3,6 (m/s)
VC = 6,0m/s
Respostas: a) Ver figura
b) 6,0m/s
6–
m = 70kg
g = 10m/s2
144
km
V = 144 –––– = –––– (m/s) = 40m/s
3,6
h
2)
R = 40m
1600
FN = 70 10 + ––––– (N)
40
FN = 3,5. 103N
A força de atrito é uma força dissipativa que transforma energia mecânica em térmica.
A força aplicada pela mola é uma força conservativa que
transforma energia potencial elástica em energia cinética ou
vice-versa.
Resposta: A
Resposta: C
3)
9)
a)
mV2
Fcp = ––––
R
3,0 . 16,0
Fcp = –––––––––– (N) ⇒
2,0
Fcp = 24,0N
b)
P – FN = Fcp
FN = P – Fcp
FN = (30,0 – 24,0) (N)
FN = 6,0N
a) A distância percorrida pela base do tubo até atingir a
cabeça do executivo corresponde à altura H = 3,2m.
Usando-se a Equação de Torricelli:
A força normal que o carrinho troca com o apoio corresponde ao seu peso aparente.
Respostas: a) 24,0N
b) 6,0N
V2 = V02 + 2s
V2f = 0 + 2 . 10 . 3,2
P – FN = Fcp
FN = P – Fcp
10)
Vf = 8,0m/s
mV 2
FN = mg – –––––
R
V2
FN = m g – ––––
R
b) O trabalho do peso é dado por:
τP = – m g H
τP = – 450 . 10 . 5,5 (J)
τP = – 24750 J
400
FN = 2,0 . 103 10 – –––– (N)
100
Respondendo com notação científica e com dois algarismos significativos, temos:
τP = – 2,5 . 104 J
FN = 1,2. 104N
Respostas: a) 8,0m/s
b) –2,5 . 104J (aproximadamente)
P = 2,0 . 104N
FN
–––– = 0,60 ⇒ FN = 0,60P
P
4)
A força de tração aplicada pelo fio faz o papel de resultante
centrípeta e, por ser normal à trajetória, não realiza trabalho.
Resposta: A
5)
a) 1) A distância percorrida, em relação à esteira, é dada por:
FN = 60%P
Resposta: C
n Módulo 23 – Trabalho
1)
τF = τFx = Fx . d
A componente Fy não realiza trabalho porque é perpendicular ao deslocamento.
τF = 15 . 2,0 (J)
τF = 30J
Resposta: D
d = V . t
7,2
d = ––––– . 40 . 60 (m)
3,6
d = 4,8 . 103m = 4,8km
2) O deslocamento vetorial do jovem, em relação ao solo
terrestre, é nulo.
–7
b)
FRENTE 2 ÓPTICA
n Módulo 19 – Reflexão Total
1)
a) Para incidência não ortogonal, a luz sofre desvio, afastando-se da normal no ponto de incidência, quando se refrata
no sentido do meio mais refringente para o meio menos
refringente.
b) A luz deve incidir do meio mais refringente para o meio
menos refringente, segundo um ângulo de incidência
maior do que o ângulo limite para o dioptro.
Respostas: a) Afasta-se.
b) nA > nB e o ângulo de incidência deve superar o ângulo
limite.
2)
Para qualquer posição relativa entre o peixe e a gaivota,
sempre existirão raios de luz que se propagam do peixe para
a gaivota, sofrendo refração entre a água e o ar, sob ângulo
de incidência menor do que o ângulo limite para o dioptro:
1) A força que movimenta a esteira é a força de atrito que
o jovem aplica com seus pés:
2) A energia consumida para movimentar a esteira é dada
por:
E = 300kcal = 300 . 103 . 4,0J
E = 1,2 . 106J
Esta energia pode ser medida pelo trabalho realizado
pelo jovem, que é equivalente a:
τ=F.d
1,2 . 106 = F . 4,8 . 103
F = 2,5 . 102N
Respostas: a) 4,8km e zero
b) esquema e 2,5 . 102N
6)
Resposta: E
3)
1) Na direção vertical, temos:
FN + Fy = P
FN + F sen 37° = mg
FN + 250 . 0,60 = 1000 ⇒
FN = 850 N
2) O trabalho do atrito é dado por:
τat = Fat . d . cos 180°
τat = d FN . d (– 1)
τat = – 0,50 . 850 . 10 (J)
τat = – 4250 J
(I)
Cálculo de sen L:
1,0
nar
sen L = ––––– = –––––
5
nlíq
–––
3
3
sen L = ––––
5
(II) Cálculo de cos L:
Resposta: E
8–
sen2 L + cos2 L = 1
3
–––
5
2
7)
+ cos2 L = 1
Da qual:
4
cos L = ––––
5
(III) Cálculo de p:
sen L
r
tg L = ––––– = –––
cos L
p
3
––––
5
3
––––– = –––
4
p
––––
5
(IV)
Para que ocorra reflexão total do feixe de luz na superfície
AB:
90° – θ > L
⇒
sen (90° – θ) > sen L
p = 4m
nAr
cos θ > ––––
nV
Parte não vista da palavra: FÍSI
Parte vista da palavra: CA
Do gráfico, para λ = 400 nm, tem-se nV = 1,47, logo:
Resposta: C
4)
5)
1
cos θ > ––––
1,47
A fibra é feita de material com elevado índice de refração absoluto e, por isso, o ângulo limite de incidência é relativamente pequeno e ocorre, intensamente, o fenômeno de reflexão total da luz.
Resposta: A
O menor valor possível para cos θ é tal que:
Deve-se notar que ao menor valor de cos θ corresponde o
maior valor de θ (1.o quadrante).
Resposta: E
O ângulo limite L é dado por:
nmenor
sen L = –––––––
nmaior
8)
Em dias quentes, uma camada de ar mais próxima do solo é
aquecida, diminuindo seu índice de refração absoluto em
relação à camada de ar mais fria imediatamente superior.
Assim, para um observador, convenientemente posicionado,
pode ocorrer o fenômeno da reflexão total quando a luz se
propaga da camada de ar mais fria (índice de refração maior)
para a camada de ar mais quente, de índice de refração
menor. O observador poderá então ver no solo uma imagem
refletida do céu. Como a imagem do céu refletida no solo
ocorre pela reflexão da luz em uma superfície de água – uma
poça, por exemplo –, o observador interpreta que a superfície
do asfalto está coberta por uma camada de água.
Resposta: B
9)
O índice de refração absoluto diminui com o aumento da altitude e, portanto, o raio de luz aproxima-se cada vez mais da
normal.
nar
1
sen L = –––––– = ––––––
nvidro
nvidro
1
sen (45°) = ––––––
nvidro
2
nvidro = Resposta: A
6)
a) A luz sofre refração e reflexão.
b) No ponto B da interface entre o vidro e o ar, a luz incide
sob ângulo α, tal que:
α + 90° + 40° = 180°
α = 50°
Como o ângulo limite L é de 42°, a luz incide sob ângulo
maior do que o ângulo limite e sofre reflexão interna total
em B:
1
cos θ –––––
1,47
n Módulo 20 – Lentes Esféricas
1)
A figura representa uma lente de bordas espessas. Para
descobrirmos se a lente será convergente ou divergente,
precisamos analisar seu índice de refração. Se o índice de
refração da lente for nL e o da água for nA, teremos:
nL
nA
nL
Se nL > nA, divergente, ou –––– > –––– , então –––– > 1 e
nA
nA
nA
teremos uma lente divergente. Como o índice de refração n
Respostas: a) A luz sofre refração e reflexão.
b) Vide esquema.
nL
dado no exercício corresponde a n = –––– , se n > 1 teremos
nA
uma lente divergente.
Resposta: A
–9
2)
Como a luz atravessa a caixa, o elemento óptico no meio dela
precisa ser transparente para permitir a passagem dos raios.
Além disso, os raios que saem são desviados para fora; logo
o elemento óptico deve ser uma lente divergente.
Resposta: B
3)
Para queimar a folha de papel, o estudante necessita concentrar os raios de luz do sol. Ele consegue realizar este feito
se utilizar lentes convergentes, neste caso representadas por
lentes de bordas finas, I e III.
Resposta: B
4)
Como a lente é plano-convexa, ela tem bordas finas. Como o
índice de refração do vidro é maior que o do ar, concluímos
que a lente será convergente.
Resposta: B
9)
10) a) A lente L1 é convergente, pois a imagem formada é maior,
virtual e direita. Já a lente L2 é divergente, pois a imagem
formada é menor, virtual e direita.
b) L1: virtual, aumentada, direita / L2: virtual, diminuída,
direita.
n Módulo 21 – Estudo Analítico e
Vergência de uma Lente
1)
5)
6)
7)
Notamos na figura que a imagem das letras é menor, direita
e virtual em relação à página do livro; logo, a lente utilizada
é divergente. Ao se aproximar a lente dos olhos, ela vai afastando-se da página do livro, tornando a imagem cada vez
menor, sem mudar as outras características.
Resposta: A
O formato da bolha indica que se trata de uma lente biconvexa, portanto de bordas finas. Como o índice de refração do
ar que forma a bolha é menor que o do vidro, a lente de
bordas finas será divergente.
Resposta: B
A distância focal vale f, a distância do objeto à lente é p = 3f.
Para se descobrir a distância entre o objeto e a imagem, é
preciso antes encontrar p', a distância da lente à imagem.
Usando-se Gauss, obtém-se:
1
1
1
1
1
1
1
1
1
––– = ––– + ––– ; ––– = ––– + ––– ; ––– = ––– – ––– ;
f
p
p’
f
3f
p’
p’
f
3f
1
3
1
1
2
––– = ––– – ––– ; ––– = ––– ;
p’
3f
3f
p’
3f
Se colocássemos o objeto em B, obteríamos uma situação
análoga à da figura, na qual o objeto se encontra no ponto
antiprincipal da lente e a imagem também.
Resposta: A
3f
p’ = –––
2
Esquematicamente, tem-se:
a)
Logo, a distância entre objeto e imagem será:
d = p + p'
3f
d = 3f + –––
2
b) Como a imagem é formada pelos prolongamentos do
raios originais refratados, ela é virtual.
8)
a) A imagem é invertida e menor que o objeto; então a lente
será necessariamente convergente.
b)
9f
d = –––
2
Resposta: E
2)
Para descobrirmos a distância p’ da imagem à lente, dada a
distância focal f = 6,0cm e a distância do objeto à lente,
p = 30cm, fazemos:
1
1
1
1
1
1
1
1
1
––– = ––– + ––– ; ––– = ––– + ––– ; ––– = ––– – ––– ;
f
p
p’
6
30
p’
p’
6
30
1
5
1
1
4
––– = ––– – ––– ; ––– = –––
p’
30
30
p’
30
C : centro óptico
F’ : foco imagem principal
F : foco objeto principal
A : ponto antiprincipal objeto
A’ : ponto antiprincipal imagem
10 –
30
p’ = ––– cm
4
p' = 7,5cm
Resposta: E
3)
Na primeira situação, como o objeto está muito afastado da
lente, p = ∞. Também é dado p’ = 6cm. Assim:
f
4
A = ––––– ; – 1 = –––––– ; – 4 + p1 = 4cm ⇒ p1 = 8cm
f – p1
4 – p1
1
1
1
1
1
1
1
1
––– = ––– + ––– ; ––– = ––– + ––– ; ––– = –––
∞
f
p
p’
f
6
f
6
Na segunda situação, aproximando a lente do objeto,
teremos p2 = p1 – 2cm; p2 = 6cm. Para encontrarmos a
distância x entre as imagens da primeira e da segunda
situação, assim como o novo aumento linear A2,
precisamos encontrar p’1 e p’2.
Situação 1:
f = 6,0cm
Na segunda situação, p = 18cm, e a distância p’ da imagem à
lente será:
1
1
1
1
1
1
––– = ––– + ––– ; ––– = ––– + ––– ;
f
p1
p’1
4
8
p’1
1
1
1
1
1
1
1
3
1
––– = ––– + ––– ; ––– = ––– + ––– ; ––– = ––– – ––– ;
f
p
p’
6
18
p’
p’
18
18
1
1
1
1
2
1
––– = ––– – ––– ; ––– = ––– – –––
p’1
4
8
p’1
8
8
1
2
––– = –––
p’
18
p’1 = 8cm
Situação 2:
p’ = 9,0cm
1
1
1
1
1
1
––– = ––– + ––– ; ––– = ––– + ––– ;
f
p2
p’2
4
6
p’2
Resposta: C
4)
1
1
1
1
Como ––– equivale a ––– e ––– equivale a ––– , para enconx
p
y
p’
trar a distância
coordenadas
focal,
podem-se
utilizar
1
1
1
1
3
2
––– = ––– – ––– ; ––– = ––– – –––
p’2
4
6
p’2
12
12
quaisquer
p’2 = 12cm
1
1
de um ponto do gráfico. Usando-se ––– = 5 e ––– = 0 (0;5),
x
y
x = p’2 – (p’1 + d)
x = 12 – (8,0 + 2,0)
1
1
1
1
1
1
tem-se: ––– = ––– + ––– ; ––– = 5 + 0; ––– = 5; f = ––– m =
f
x
y
f 0,2m
f
5
x = 2,0cm
– p’
– 12
b) A2 = ––––2 ; A2 = ––––
p2
6
Resposta: D
5)
A2 = –2
Deseja-se descobrir f e a posição de uma lente em relação ao
objeto, o que significa encontrar p.
Temos A =
i
–––
o
– 1,0
= ––––– =
4,0
1
– ––– = A , e temos que a
4
d i s t â n c i a
Respostas: a) 2,0cm
b) –2,0
7)
Para falarmos sobre as vergências V1 e V2, podemos analisar
as distâncias focais f1 e f2. Como raios que incidem
paralelamente ao eixo principal se refratam pelo foco da
lente, vemos que a e b correspondem às distâncias focais, em
que a = f1 e b = f2. Como f1 < f2, então V1 > V2, pois a vergência
é inversamente proporcional à distância focal.
Resposta: C
8)
Se a imagem é real, invertida e de mesmo tamanho, significa
que o objeto e a imagem se encontram sobre os pontos antiprincipais da lente.
entre objeto e imagem vale 100cm. Assim, p + p’ = 100cm.
– p’
1
p
p
5p
A = ––– = – ––– → p’ = –––– ; p + ––– = 100; ––– = 100;
p
4
4
4
4
4 . 100
p = ––––––
5
p = 80cm
A distância x será:
f
1
f
A = –––– ; – –– = –––––– ; – 1 (f – 80) = 4f; – f + 80 = 4f; 5f = 80;
f–p
4
f – 80
f = 16cm
6)
a) Temos f = 4cm e, dados na primeira situação, um
aumento linear A = – 1. Com estes, podemos encontrar a
posição p1 do objeto na primeira situação.
– 11
Usando-se a Equação dos pontos conjugados de Gauss,
tem-se:
Se a distância entre o objeto e a imagem vale 4,0m, nesta
configuração a distância do objeto à lente vale 2,0m e, como
o objeto está sobre o ponto antiprincipal, que dista duas
distâncias focais da lente, a distância focal será f = 1m.
1
1
Assim V = ––– = ––– = 1di;
f
1
1
1
1
––– + –––– = –––
p
p’
f
V = 1,0di
1
1
––– + –––– =
p
p’
Resposta: A
ncrist
––––––– – 1
nar
2
–––
R
– 1
––––––
n
ncrist
9)
n2
Dados: ––– = 1,5; R1 = +4,0cm (convexa); R2 = +6,0cm (convexa);
n1
ar
R = –––––––––––––– 2
1
1
––– + –––
p
p’
busca-se f:
1
––– =
f
n2
––– – 1
n1
1
––– = 0,5 .
f
1
1
––– + –––
R1
R2
3
2
––– + –––
12
12
24
f = ––– = 4,8cm;
5
1
; ––– = (1,5 – 1)
f
1
1
––– + –––
4
6
Os valores de ncrist, nar e p’ (profundidade do olho) são
constantes. Se o objeto se aproxima do observador, p
diminui de valor e o denominador na expressão de R
aumenta e então R diminui.
c) A acomodação visual a é dada por:
1
1
5
5
; ––– = ––– . ––– = –––
f
2
12
24
1
1
a = –––––– – –––––
Prem
Ppróx
f = 4,8m
Para um olho normal:
Resposta: C
Ppróx 0,25m
1
–––––– → 0
Prem
10) Para acharmos a convergência equivalente V, devemos
somar as vergências individuais:
1
1
1
1
V = V1 + V2; V = ––– + ––– ; V = ––– + ––– ;
f1
f2
0,1
0,4
V = 10 + 2,5 (di) = 12,5di;
1
a ––––– – 0 (di)
0,25
V = 12,5 di
a 4,0di
Resposta: D
Respostas: a) Real, invertida e menor em relação ao objeto.
b) Diminui.
c) a 4,0di
11)
Como os raios que incidem na primeira lente são paralelos e
os emergentes da segunda também, as posições dos focos F1
e F2 das duas lentes devem coincidir. Logo, d = f1 + f2.
Resposta: A
2)
Com os músculos ciliares relaxados, máxima distância focal
ocular, a imagem de um objeto distante se forma antes da
retina, posição (1), para o olho míope; na retina, posição (2),
para o olho normal; após a retina, posição (3), para o olho
hipermetrope.
Resposta: A
3)
Lente convergente para a hipermetropia e divergente para a
miopia.
Resposta: E
4)
O astigmatismo pode ser corrigido mediante o uso de lentes
cilíndricas.
Resposta: E
5)
Na presbiopia, o indivíduo perde a capacidade de
acomodação por um enrijecimento natural dos músculos
ciliares que altera a forma do cristalino.
Resposta: D
6)
Persistência retiniana.
Resposta: B
n Módulo 22 – Óptica da Visão
1)
a) Real, invertida e menor em relação ao objeto.
b) Supondo-se que o cristalino se comporte como uma lente
esférica biconvexa, com faces de mesmo raio de curvatura
R, da Equação de Halley obtém-se:
1
––– =
f
12 –
ncrist
––––––– – 1
nar
2
–––
R
7)
Como o ponto remoto da pessoa está muito próximo de seu
globo ocular, a pessoa sofre de miopia:
1
Vmíope = –––––
Prem
Vmíope
3)
Feixes de partículas: a e b
Ondas eletromagnéticas: c, d, e, f, g, h, i e j
Ondas mecânicas: k, l, m e n
4)
A luz do relâmpago propaga-se quase instantaneamente do
ponto da queda do raio até o observador. O som se propaga
com velocidade de intensidade V = 340m/s.
1
= ––––– (di)
0,50
s
V = –––
t
Vmíope = 2,0di
Resposta: C
8)
s
340 = –––
20
a) Lente divergente.
b) fmíope = – Prem
fmíope = – 20cm
s = 1020m = 1,02km
Respostas: a) Lente divergente.
b) fmíope = -20cm
Resposta: s = 1020m = 1,02km
5)
9)
Da Equação dos pontos conjugados de Gauss, obtemos:
1
1
1
––– + –––– = –––
p
p’
f
Se p é a profundidade do mar, o ultrassom viaja uma
distância de 2p entre a emissão do sinal, sua reflexão no
fundo do mar e sua recepção pelo barco. A intensidade V da
velocidade do ultrassom na água é, então, dada por:
1
1
1
––––– + –––– = ––––
150
p’
– 30
s
V = –––
t
p’ = – 25cm
2p
1500 = –––
1,0
d = .p’. = 25cm
p = 750m
Resposta: d = 25cm
Resposta: p = 750m
10) O ponto próximo da pessoa está muito afastado de seus
olhos. A pessoa pode sofrer de hipermetropia e/ou
presbiopia.
Resposta: A
6)
11) Para a correção da hipermetropia, temos:
s
V = –––
t
1
1
1
––– – ––––– = ––––
25
Ppróx
fhip
2d
340 = –––
6,0
1
1
1
–––– – –––– = ––––
25
75
fhip
d = 1020m
fhip = 37,5cm
Resposta: fhip = 37,5cm
n Módulo 23 – Classificação das Ondas e
Velocidade do Som e da Luz
1)
Como o ar dentro do recipiente foi retirado pela bomba de
vácuo, o som que é uma onda mecânica de pressão não se
propaga do despertador até os alunos.
Resposta: A
Se d é a distância entre o caçador e o anteparo refletor, o som
viaja uma distância de 2d entre o disparo do tiro, sua reflexão
no anteparo e a recepção do eco pelo caçador. A intensidade
V da velocidade do som é, então, dada por:
Resposta: B
7)
A intensidade V da velocidade do som é dada por:
s
V = –––
t
No ar:
d
300 = –––––
tar
d
tar = –––––
300
Na água:
2)
Raios e raios catódicos são feixes de elétrons acelerados.
Os raios são feixes de partículas constituídas de núcleos de
átomos de hélio, com dois prótons e dois nêutrons. Os três
tipos de raios são, então, exemplos de feixes de partículas, e
não de radiações ou ondas eletromagnéticas.
Resposta: D
d
1500 = ––––––––
tágua
d
tágua = ––––––
1500
– 13
tar – tágua = 6,0s
Substituindo-se o valor de Vsom em (eq. 2), tem-se:
d
d
––––– – –––––– = 6,0s
300
1500
5000
75000
–––––– = –––––––– + Vvento
14,5
224,75
d = 2250m
Resposta: d = 2250m
8)
A intensidade V da velocidade é dada por:
s
V = –––
t
Para a bala:
340
170 = ––––––
tbala
tbala = 2,0s
O tempo total entre o disparo da bala e a recepção do som
pelo homem é dado pela soma entre o tempo de viagem da
bala tbala do homem até o alvo e o tempo de retorno do som
do alvo até o homem tsom:
tbala + tsom = 3,0s
2500
Vvento = –––––––– m/s
224,75
Vvento 11,1m/s
Respostas: Vsom 333,7m/s
Vvento 11,1m/s
10) a) Ao se propagar no ar, o som viaja com uma velocidade Var
dada por:
sar
Var = ––––––
tar
510
340 = –––––
tar
tar = 1,5s
2,0 + tsom = 3,0s
tsom = 1,0s
Para o som:
340
Vsom = ––––– (m/s)
1,0
b) Ao se propagar no trilho de aço, o som viaja com uma
velocidade Vaço dada por:
saço
Vaço = ––––––
taço
Vsom = 340m/s
Resposta: Vsom = 340m/s
9)
A intensidade da velocidade resultante VRES entre a velocidade do som Vsom e a do vento Vvento é dada por:
AB
VRES = ––––– = Vsom – Vvento t
Adotando-se a orientação de A para B, tem-se:
(1) Observador A ouve o disparo de B
5000
–––––– = Vsom – Vvento (eq. 1)
15,5
(2) Observador B ouve o disparo de A:
5000
–––––– = Vsom + Vvento (eq. 2)
14,5
Nos dois trechos retilíneos do trilho, o som viaja uma
distância de 6600m. No trecho curvilíneo, o som viaja uma
distância d dada por:
2πr
d = –––––
2
d = πr = 3 . 255(m)
d = 765m
saço = 6600m + 765m
saço = 7365m
Como o trabalhador percebe simultaneamente os sinais
pelo ar e pelo aço, temos que:
taço = tar = 1,5s
Portanto:
Da soma entre (eq. 1) e (eq. 2), resulta:
5000
5000
–––––– + –––––– = 2Vsom
15,5
14,5
75000
Vsom = –––––––– m/s
224,75
Vsom 333,7m/s
14 –
7365
Vaço = –––––– (m/s)
1,5
Vaço = 4910m/s
Respostas: a) tar = 1,5s
b) Vaço = 4910m/s
FRENTE 3 – ELETRICIDADE
n Módulo 19 – Campo Magnético do Condutor Retilíneo e da Espira
1)
– 15
2)
16 –
3)
Vejamos a situação da figura por cima.
4)
Conforme a regra da mão direita, ao alinharmos o dedão da
mão com a linha azul do fio, ao girarmos a mão percebemos
que os dedos “saem”do papel por cima da linha azul e
“entram” no papel por baixo da linha.
Resposta: A
5)
Sem corrente no fio, as bússolas alinham-se com o campo
magnético terrestre.
Na segunda situação, as bússolas se alinharão conforme o
campo magnético resultante da soma vetorial do campo
magnético terrestre com o externo, dado pela corrente que
circula pelo fio.
Resposta: C
Situação 1: sem corrente. Há apenas campo magnético
terrestre.
– 17
→
By
Situação 2: com corrente.
Na situação 2, B e D conseguirão alinhar-se ao campo magnético resultante, já C ficará inalterada.
→
By
Resposta: D
6)
→
→
– Bx = 0
→
= Bx
µ . 3i
µ.i
y
; ––––––– = –––––– ; –– = 3
2πy
2πx
x
Resposta: A
No 1.° caso, para uma corrente I, pela Lei de Biot-Savart,
.I
temos B = ––––– . Quando a corrente é 3I, temos, no 2.° caso,
2π d
10) Usamos a regra da mão direita para desenhar os campos
magnéticos gerados por I’ e I’’.
µ . 3I
µ.I
B2 = ––––– = 3 ––––– = 3B
2π d
2π d
Resposta: D
7)
Os campos só podem anular-se em II e IV, pois somente
nesses quadrantes os campos têm sentidos opostos.
Resposta: D
n Módulo 20 – Indução Eletromagnética
Efetuando a regra da mão direita para cada um dos fios,
temos a configuração dos campos no ponto C. Efetuando a
soma vetorial, teremos resultante necessariamente na
direção de AA’.
8)
1)
Só há corrente induzida quando há variação do fluxo
magnético.
Resposta: A
2)
Quando há variação do fluxo magnético, gera-se corrente
induzida no condutor.
Resposta: C
3)
Se a velocidade relativa entre o ímã e o condutor for nula,
não há variação do fluxo magnético, logo não haverá
corrente induzida.
Resposta: E
4)
0: Falso: Se houver aproximação ou afastamento, haverá
corrente.
1: Verdadeira.
Resposta: D
9)
2: Verdadeira.
→
→
Os vetores Bx e By têm sua direção e seus sentidos dados
pela regra da mão direita. Para que o campo magnético seja
nulo em P, temos:
18 –
3: Falsa. Veja figura explicativa da proposição 1.
4: Verdadeira. O movimento relativo entre ímã e anel é o
mesmo descrito na posição 1.
5: Falsa. A Lei de Faraday-Lenz assegura o surgimento de
corrente induzida se houver movimento relativo entre
anel e ímã.
5)
A geração de eletricidade em hidroelétricas exige que haja a
variação de fluxo magnético para gerar corrente induzida.
Essa variação de fluxo se dá girando um eletroímã, usando a
queda da água para movimentá-lo.
Resposta: A
6)
I: Verdadeira: Como a área diminui com o tempo, o fluxo
magnético também diminui.
II: Verdadeira: Como o fluxo magnético está diminuindo, a
corrente induzida circula de forma a gerar um campo
magnético que se oponha a essa diminuição. Nesse caso,
o campo induzido terá a mesma direção que o campo
externo, para fora do papel, o que por sua vez
corresponde a uma corrente no sentido anti-horário.
III: Falsa:
9)
→
A corrente induzida na espira 2 gera um campo induzido Bi
que deve opor-se à variação de fluxo magnético do campo
gerado pela espira 1.
→
→
Se o fluxo diminuir, Bi concordará com a direção do campo B1
→
→
em diminuição. Nesse caso, 䊟 Bi e 䊟 B1 serão os sentidos
dos campos, o que significa que a corrente da espira 1 estará
no sentido anti-horário.
→
→
Se o fluxo aumentar, Bi 䊟 e B1 䉺 serão os sentidos dos campos e a corrente da espira 1 estará no sentido anti-horário.
Resposta: D
n Módulo 21 – Eletrização Por Atrito,
Contato e Indução
1)
A corrente elétrica pode ser calculada pela expressão
Q
i = ––––
t
Em termos de unidades, temos:
coulomb (C)
ampère (A) = –––––––––––––
segundo (s)
Como o sentido da corrente é anti-horário, a força magnética, pela regra da mão esquerda, terá direção oposta à da
velocidade.
Resposta: D
ou, ainda: C = A . s
Resposta: A
2)
Um corpo está eletricamente neutro quando as quantidades
de prótons e elétrons são iguais.
Logo, se o corpo ficou eletrizado, então essas quantidades
tornaram-se diferentes. Como a quantidade de núcleos não
foi alterada, devemos concluir que a quantidade de elétrons
mudou.
Resposta: D
3)
O atrito entre duas substâncias da tabela deixa a primeira
delas eletrizada positivamente e a segunda, negativamente.
a) Lã: positiva; ebonite: negativa
b) Vidro: positiva; algodão: negativa
c) Adquiriram cargas opostas e, portanto, se atraem.
7)
→
A corrente no sentido anti-horário gera um campo induzido Bi
para fora do papel. Pela direção da velocidade, o fluxo de
→
→
campo magnético externo Bext está aumentando. Como Bi
→
deve opor-se a esse aumento de fluxo, se Bi é para fora do
→
papel, Bext aponta para dentro.
Resposta: A
4)
8)
Q: carga da esfera
n: quantidade de elétrons
e: carga elementar
Q=n.e
Q = 2,0 . 1010 . (–1,6 . 10–19)(C)
Q = – 3,2 . 10–9C
Não há fluxo magnético nessa situação. O ângulo entre a
normal à área e as linhas de indução é 90°.
Φ = B . A . cosx = B . A . cos90° = 0
Logo não haverá corrente induzida.
Resposta: A
5)
QA = + 1,6 . 10–12C
QB = – 4,8 . 10–12C
QA + QB
(+1,6 . 10–12) + (–4,8 . 10–12)
Q’A = Q’B = ––––––––– = ––––––––––––––––––––––––– (C)
2
2
Q’A = Q’B = –1,6 . 10–12C
– 19
6)
1.° contato
QA + QB
Q+ 0
Q
Q’A = Q’B = ––––––––– = –––––– = –––
2
2
2
2.° contato
Q’A + QC
Q/2 + 0
Q
Q’’
A = Q’C = ––––––––– = ––––––– = –––
2
2
4
3.° contato
Q’’
Q/4 + 0
Q
A + QD
Q’’’
A = Q’D = ––––––––– = ––––––– = –––
2
8
2
Sendo Q a carga inicial de A, sua carga após os 3 contatos é
Q
––– .
8
7)
Um corpo é considerado isolante quando as cargas em
excesso que adquire não conseguem movimentar-se e
permanecem no local onde foram “depositadas”. O metais
são bons condutores de carga e, portanto, não são isolantes.
Resposta: E
8)
Após o contato, ambas passam a ter a mesma carga, dada
pela média aritmética das cargas iniciais:
Q + (–2Q)
Q
––––––––––– = – –––
2
2
Após a eletrização, a força de tração equilibra a soma da força
peso da esfera com a força de repulsão elétrica.
Resposta: C
Resposta: C
9)
Q1 = Q; Q2 = Q; Q3 = 0
1.° contato
Q1 + Q3
Q+ 0
Q
Q’1 = Q’3 = ––––––––– = –––––– = –––
2
2
2
2.° contato
Q2 + Q’3
Q + Q/2
3Q
Q’2 = Q’’
3 = ––––––––– = –––––––– = ––––
2
2
4
Portanto, a carga final de 1 é Q/2 e a carga final de 2 é 3Q/4.
Resposta: C
10) QA = 8C; QB = 0; QC = 0
12) O processo de eletrização por contato ocorre quando há
diferença de carga entre os corpos, não ocorrendo, portanto,
para ambos neutros.
No processo de eletrização por indução, um dos corpos deve
estar eletrizado (indutor) para provocar polarização no outro
corpo.
Resposta: D
13) O eletroscópio carrega-se positivamente por contato com a
esfera. As folhas do eletroscópio, ambas com cargas
positivas, se repelem e se afastam, como mostra a figura da
alternativa b.
Resposta: B
1.° contato
QA + QB
8+ 0
Q’A = Q’B = ––––––––– = –––––– = 4C
2
2
2.° contato
14) Duas esferas podem atrair-se, como na figura II, quando
possuem cargas opostas ou quando uma delas está carregada
e a outra, neutra, sofre polarização por indução.
Q’B + QC
4+ 0
Q’’
B = Q’C = ––––––––– = –––––– = 2C
2
2
Portanto, a esfera C adquiriu 2C.
Resposta: A
11) As esferas são idênticas e, consequentemente, adquiriram
cargas de mesmo sinal. Assim, após a eletrização, ambas se
repelem.
Antes da eletrização, a força de tração equilibra apenas a
força peso da esfera.
20 –
Resposta: B
n Módulo 22 – Força Eletrostática
1)
b) Após o contato, as novas cargas serão iguais:
Q1 + Q2
1 . 10–9 – 5 . 10–10
Q’1 = Q’2 = ––––––––– = –––––––––––––––––– (C) = 2,5 . 10–10C
2
2
Sendo ambas positivas, as partículas se repelem com uma
força dada por
A nova força entre elas tem módulo:
K0 . . Q1 . . . Q2 .
F = ––––––––––––––
d2
. Q’1 . . . Q’2 .
(2,5 . 10–10)2
F’ = K0 . ––––––––––– = 9 . 109 . ––––––––––––– (N)
d2
(0,3)2
K0 = 9 . 109 N . m2/C2
F’ = 6,25 . 10–9N
Q1 = Q2 = 8,0 . 10–6C
e como ambas são positivas, F’ é repulsiva.
→
d = 30cm = 3,0 . 10–1m
9 . 109 . . 8,0 . 10–6 . . . 8,0 . 10–6 .
F = –––––––––––––––––––––––––––––– (N)
(3,0 . 10–1)2
5)
K . . 2 . Q1 . . . 2 . Q2 .
4K . . Q1 . . . Q2 .
K . . Q1 . . . Q2 .
F = ––––––––––––––––––– = ––––––––––––––– = ––––––––––––––
(2d)2
4 . d2
d2
F = 6,4N
Resposta: A
2)
F’
⬖ ––– = 1
F
A força eletrostática entre os dois corpúsculos é dada por
. Q1 . . . Q2 .
F = K0 –––––––––––
d2
Sendo:
Resposta: C
K0 = 9 . 109N . m2/C2
6)
Q1 = Q2 = Q
d = 1,0cm = 1,0 . 10–2m
I. Correta
As cargas do próton e do elétron são iguais em módulo
(e = 1,6 . 10–19C) e o módulo da força, dado pela Lei de
Coulomb, é o mesmo nos três esquemas:
F = 3,6 . 102N
Substituindo:
e2
. Q1 . . . Q2 .
F = K . –––––––––––– = K . ––––
d2
d2
II. Correta
9 . 109 . Q2
3,6 . 102 = –––––––––––
(1,0 . 10–2)2
De acordo com a lei da ação e reação.
Q = 2. 10–6C
III. Correta
Q = 2C
IV. Errada
Resposta: E
3)
K . . Q1 . . . Q2 .
F = –––––––––––––
d2
A força é atrativa apenas no esquema 2.
. Q1 . . . Q2 .
F = K0 –––––––––––
d2
Resposta: A
7)
2Q . 3Q
0,6 = 9 . 109 . –––––––––
32
Após o contato, ambas adquirem a mesma carga, dada por:
Q1 + Q2
16 + (–4,0)
Q’1 = Q’2 = ––––––––– = ––––––––––– (C) = 6,0C = 6,0 . 10–6C
2
2
6 . 10–1 = 6 . 109 . Q2
A força de repulsão entre elas tem módulo dado pela Lei de
Coulomb:
Q2 = 1 . 10–10
Q = 1 . 10–5C
. Q’1 . . . Q’2 .
(6,0 . 10–6)2
F = K0 . ––––––––––– = 9 . 109 . ––––––––––– (N)
d2
(3,0 . 10–2)2
Q = 10 . 10–6C
Resposta: B
F = 360N
4)
a) As esferas possuem cargas opostas e por isso se atraem.
A força de atração pode ser calculada pela Lei de
Coulomb:
. Q1 . . . Q2 .
F = K0 –––––––––––
d2
sendo:
temos:
Resposta: D
8)
. Q1. . . Q2.
1
.Q1. . .Q2.
1
F’ = K0 . –––––––––– = –– . K0 . –––––––––– = –– . 0,18 = 0,02N
2
2
(3d)
d
9
9
K0 = 9 . 109N . m2/c2
Q1 = 1 . 10–9C
Q2 = –5 . 10–10C
d = 0,3m
.1.
. . . –5 .
F = 9 . 109 . –––––––––––––––––––––––– (N)
(0,3)2
–8
F = 5 . 10 N
10–9
. Q1 . . . Q2 .
a) F = K0 . ––––––––––– = 0,18N
d2
10–10 .
. 0,5 . Q1. . 0,5 . Q2. 0,25 K0 . . Q1. . . Q2. 0,25
b) F’’ = K0 . –––––––––––––––– = –––––––––––––––––– = –––– . 0,18
(0,5d)2
0,25 . d2
0,25
F’’ = 0,18N
– 21
9)
A força de atração elétrica atua como força centrípeta:
m V2
Felé = ––––––
R
→
→
12) Seja F1 a força de repulsão elétrica entre 2Q e q e seja F2 a
força de repulsão elétrica entre q e Q.
K..e...e.
m V2
––––––––––––– = ––––––
R2
R
Aplicando a Lei de Coulomb, temos:
K . e2
–––––– = m V2
R
K . . 2Q . . . q .
1 K.Q . q
F1 = ––––––––––––– = ––– ––––––––
2
(2L)
2
L2
9 . 109 . (1,6 . 10–19)2
–––––––––––––––––––– = 9,1 . 10–31 . V2
10–10
K . .q . . .Q .
F2 = –––––––––––––
L2
V = 1,6 . 106m/s
Observe que F2 = 2 F1 e a força resultante tem módulo:
Resposta: C
FR = F2 – F1 = 2 F1 – F1 = F1 .
10) A força de atração elétrica atua como força centrípeta. Seja m
a massa do corpo em movimento circular. Assim,
m V2
Felé = ––––––
R
13) Após o contato, as esferas A e C adquirem cargas + Q/2 cada
uma. Assim, a força de repulsão entre A e C, separadas por
uma distância d1, tem módulo:
K . q2
–––––– = m V2
r
K . . Q/2 . . . Q/2 .
FAC = –––––––––––––––
d12
K . q2
––––––
m.r
Se o raio da trajetória passar a valer r’ = 2r, então a nova
velocidade será:
V’ =
Kq2
–––––– =
m . r’
K.Q . q
–––––––– .
2 L2
Resposta: C
K . . –q . . . +q .
m V2
–––––––––––––– = ––––––
r2
r
V=
Portanto, a força resultante tem sentido de q para 2Q e vale
Kq2
1
–––––– = ––––
m . 2r
2
K . Q2/4
2,00 . 10–6 = –––––––––––
(2 . 10–2)2
KQ2 = 32 . 10–10
Kq2
––––––
mr
1
V’ = –––– . V
2
A força de repulsão entre C e B é dada por:
K . . Q/2 . . . Q .
K . Q2/2
KQ2
FCB = ––––––––––––––– = ––––––––––– = ––––––––––
d22
(8 . 10–2)2
128 . 104
32 . 10–10
FCB = –––––––––––– (N) = 0,25 . 10–6N
128 . 10–4
2V
racionalizando, V’ = ––––––
2
Resposta: A
11) O corpo A possui excesso de prótons e, portanto, sua carga
elétrica é positiva: qA = + nA . e, em que e é a carga elementar.
O corpo B possui excesso de elétrons e, consequentemente,
sua carga é negativa: qB = nB . e. Após o processo de eletrização, a nova carga de B passou a valer:
q’B = (– nBe) – (– 2nB . e) = + nB . e
Inicialmente, a força entre A e B vale:
Portanto, a força resultante tem módulo
FR = 2,00 . 10–6N – 0,25 . 10–6N
FR = 1,75 . 10–6N
orientada para a direita.
Resposta: B
K . . qA . . . qB .
K . . nA . e . . . –nB . e .
. nA . nB
F1 = ––––––––––––– = ––––––––––––––––––– = –––––––––––––
2
2
d
d
d2
K . e2
e após a eletrização de B, vale:
K . . qA . . . q’B .
K . . nA . e . . . nB . e .
K . e2 . nA . nB
F2 = ––––––––––––– = ––––––––––––––––––– = –––––––––––––
d2
d2
d2
14) Da Lei de Coulomb, aplicada para as partículas B e C, temos:
K . . QB . . . QC .
FBC = –––––––––––––
d2BC
das quais concluímos que F2 = F1
K . Q2
3,0 . 10–6 = –––––––––––
(3,0 . 10–2)2
Resposta: C
KQ2 = 27 . 10–10
22 –
A força entre A e B tem módulo dado por:
n Módulo 23 – Campo Elétrico
K . . QA . . . Q B .
K . Q2
27 . 10–10
FCB = ––––––––––––––– = ––––––––––– = –––––––––– (N)
2
dAB
(1,0 . 10–2)2
1,0 . 10–4
1)
O módulo do campo elétrico é dado por
K . .Q.
E = ––––––––
d2
FAB = 27 . 10–6N
Sendo
Portanto, a força resultante tem intensidade:
Q = 4,0C = 4,0 . 10–6C
K = 9,0 . 109N . m2/C2
d = 2,0mm = 2,0 . 10–3m
Temos
FR = 27 .
10–6N
– 3,0 .
9,0 . 109 . . 4,0 . 10–6 .
E = ––––––––––––––––––––– (N/C)
(2,0 . 10–3)2
10–6N
FR = 24 . 10–6N
E = 9,0 . 109N/C
Orientada para a direita.
Resposta: D
2)
15) Na situação da figura I, a carga de prova está sujeita à ação
de cinco forças repulsivas iguais.
A intensidade do campo elétrico pode ser calculada pela
expressão
F
E = ––––
.q.
Sendo
Temos
F = 0,80N
q = 2,0 . 10–6C
0,80
E = –––––––––– (N/C)
2,0 . 10–6
E = 4,0 . 105N/C
Resposta: E
3)
A intensidade do campo elétrico pode ser calculada pela
expressão
F
E = ––––
.q.
Sendo
→
Note, pela simetria da figura, que a força resultante F1 é a
→ →
→
→ →
soma vetorial entre FB , FC e FD , já que FA e FE se anulam. Na
Temos
F = 1,2N
q = 4,0C = 4,0 . 10–6C
1,2
E = –––––––––– (N/C)
4,0 . 10–6
E = 3,0 . 105N/C
situação da figura II, aparecem mais três forças atrativas, de
mesmo módulo que as cinco anteriores, nas mesmas
→ →
→
direções de FB , FC e FD .
Resposta: A
4)
De acordo com a 2.a Lei de Newton, FR = m . a
Como a força elétrica é a única força atuante, temos que
Felétrica = m . a
.q. . E = m . a
.q. . E
a = –––––––
m
Sendo
q = 4C = 4 . 10–6C
m = 5g = 5 . 10–3kg
→ → →
→
Logo, a soma vetorial entre FF , FG e FH é exatamente igual a F1 ,
→
o que nos fornece uma força total resultante 2F1 .
Resposta: E
E = 3 . 103N/C
Temos:
4 . 10–6 . 3 . 103
a = –––––––––––––––– (m/s2)
5 . 10–3
a = 2,4m/s2
Resposta: A
– 23
5)
orientado para fora dela, como nos casos das figuras 1 e 2, e
Note que a distância entre P e Q é o dobro da distância entre
B e Q:
orientado para a partícula quando ela é negativa, como
dp = 2dB
mostra a figura 3.
→ →
Na figura 1, F e E possuem o mesmo sentido e, portanto, q
Os módulos do campo elétrico em B e em P são calculados
por:
O campo elétrico de uma partícula positiva é radial e
é positiva.
→ →
Nas figuras 2 e 3, F e E possuem sentidos contrários, logo q
é negativa.
Resposta: C
K . .Q.
K .Q.
K .Q.
1
1
Ep = ––––––––– = ––––––––– = –– ––––––––– = –– . 24N/C
4
4
dp2
(2dB)2
dB2
O módulo do campo elétrico é calculado por
Ep = 6,0 N/C
Assim, apenas as afirmações I e III são verdadeiras.
6)
K . .Q.
E = ––––––––
d2
Note que E e d2 são grandezas inversamente proporcionais,
cujo gráfico é representado corretamente pela alternativa e.
Resposta: E
7)
O módulo do campo elétrico é dado por
K . .Q.
E = ––––––––
d2
Para outra situação, na qual
. Q’ . = . 2Q .
d’ = 3d
tem-se
K . . Q’ .
K . . 2Q .
2K . Q .
E’ = –––––––– = –––––––– = ––––––––
2
2
(d’)
(3d)
9d2
2
E’ = –– E
9
8)
K . .Q.
EB = ––––––––– = 24N/C
dB2
O campo elétrico de uma partícula é radial. As retas suportes
dos vetores que representam o campo nos pontos A e B
devem encontrar-se no local em que se situa a carga
geradora do campo.
24 –
Resposta: D