TA05_MAT9AB - Teste de Avaliacao

Escola E.B. 2,3 Eng. Nuno Mergulhão – Portimão
Ano Letivo 2012/2013
Teste de Avaliação Escrita
scrita de Matemática – 9.º ano de escolaridade
Duração do Teste: 90 minutos | 25 de fevereiro de 2013
Nome: _________________________________________________________
_________________________________ N.º ______
________ Turma: ____
Classificação:
Fraco (0% − 19%)
Suficiente (50% − 69%)
Insuficiente (20% − 49%)
Bom (70% − 89%)
O Professor (Nuno Marreiros):
): ____________________
__________
Muito Bom (90% − 100%)
O Encarregado de Educação: _________________________
___________________
Atenção:
Lêê atentamente o enunciado e responde apenas ao que te é pedido;
Apresenta
senta todos os cálculos que efetuares
efe
e mostra como chegaste à tua resposta;
Utiliza
tiliza apenas caneta ou esferográfica de tinta indelével, azul ou preta.
Não é permitido o uso de corretor,
tor, não sendo corrigido
corrigid nenhum item onde este tenha sido usado.
1. No ponto D existe um radar que deteta
dete qualquer barco num raio de 20 Km e no ponto
pont C existe outro radar que
deteta barcos num raio de 25 Km.
Indica qual a afirmação verdadeira:
O barco 1 não é detetado
tado por nenhum dos radares.
tado por um dos radares.
O barco 2 é apenas detetado
O barco 3 é detetado
tado pelos dois radares.
O barco 4 não é detetado
tado por nenhum dos radares.
2. Na figura está representada uma circunferência de centro O em que:
• A, B, C e D são pontos da circunferência;
•
50°
•
60°
Qual é, em graus, a amplitude do arco CB ?
Mostra como chegaste à tua resposta.
3. Na figura ao lado, está representada
da uma circunferência de centro no ponto O e
diâmetro AB. O ponto C pertence à circunferência.
Determina, em graus, a amplitude do ângulo α .
Apresenta os cálculos que efetuares.
tuares.
1
4. Na figura estão representados um retângulo
e uma circunferência de centro no ponto O e raio r.
Sabe-se que:
• o ponto E pertence à circunferência e é exterior ao retângulo
•
e
são diâmetros da circunferência
• o lado
do retângulo é tangente à circunferência
•
25°
a) Admite que o perímetro do retângulo
é igual a 36 cm.
Determina o comprimento da circunferência.
Apresenta o resultado em centímetros, arredondado às décimas.
Mostra como chegaste à tua resposta.
Nota: Sempre que, em cálculos intermédios, procederes a arredondamentos, conserva, no mínimo, duas casas decimais.
b) Determina a amplitude de uma rotação de centro em O que transforme o ponto D no ponto E.
Mostra como chegaste à tua resposta.
c) Qual das afirmações seguintes é verdadeira?
O ponto B pertence à mediatriz do segmento de reta
O ponto B pertence à mediatriz do segmento de reta
O ponto O pertence à mediatriz do segmento de reta
O ponto O pertence à mediatriz do segmento de reta
5. Na figura apresenta-se parte de um polígono regular com n lados,
podendo verificar-se que a amplitude do seu ângulo interno é
− 2380 ° e a amplitude do seu ângulo externo é
+ 10 ° .
Determina n. Mostra como chegaste à tua resposta.
2
6. Na figura podes observar uma parte de um cilindro com 8 cm de altura. O
ponto C é o centro de uma das bases desse cilindro.
Determina o volume do sólido.
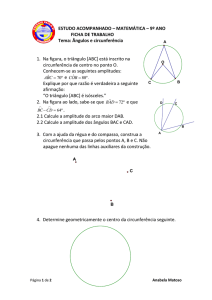
7. Na figura, sabe-se que:
• O é o centro da circunferência;
• AB e BC são cordas congruentes;
• D é o ponto de interseção do diâmetro EB com a corda AC.
Nota: A figura não está construída à escala.
a) Qual é, em graus, a amplitude do arco AC, supondo que
32° ?
b) Qual é, em centímetros, a medida do comprimento de DE, supondo que
Apresenta os cálculos que efetuares.
= 7,4
e
= 4,8
?
8. Na figura está representada uma circunferência.
A figura não está desenhada à escala.
Sabe-se que:
• os pontos A, B, C e D pertencem à circunferência
• o ponto P é o ponto de interseção das cordas AC e BD
• a amplitude do arco BC é 80º
• a amplitude do ângulo DPC é 85º
a) Determina a amplitude, em graus, do ângulo DBA.
Apresenta os cálculos que efetuares.
3
b) Os triângulos ABP e DCP são semelhantes.
Admite que:
•
2×
• a área do triângulo DCP é 24 cm2
Qual é a área, em cm2, do triângulo ABP ?
6
12
15
18
9. Observa a figura onde está representada uma circunferência de centro G, na qual está inscrito o hexágono regular
ABCDEF. Sabendo que AG = 6 cm, determina:
a) A amplitude, em graus, do ângulo ACE.
b) O comprimento, em cm, do arco AE.
c) GM , sabendo que M é o ponto médio do segmento de reta AF.
d) A área do paralelogramo AFEG.
e) A área interior à circunferência e exterior ao hexágono, arredondando o resultado à unidade.
f) O triângulo AGB é:
isósceles
equilátero
retângulo
escaleno
Agora que terminaste o teste, faz a tua avaliação sobre como te correu, assinalando as opções que melhor se identificam contigo:
Nível esperado
1
2
3
4
O teste correu-me
5
Mal
Razoável
Para o teste estudei
Bem
Nada
Pouco
O suficiente
Muito
4
Escola E.B. 2,3 Eng. Nuno Mergulhão – Portimão
Ano Letivo 2012/2013
Teste de Avaliação Escrita de Matemática – 9.º ano de escolaridade
Duração do Teste: 90 minutos | 25 de fevereiro de 2013
PROPOSTA DE RESOLUÇÃO
1. Afirmação verdadeira “O barco 4 não é detetado por nenhum dos radares.”
2. A amplitude de um ângulo inscrito é metade da amplitude do arco compreendido entre os seus lados, logo
DB = 2 × B AD = 100º .
A amplitude de um ângulo ao centro é igual à amplitude do arco compreendido entre os seus lados,
logo DC = COD = 60º . Assim, CB = DB − DC = 100º −60º = 40º .
3. Os ângulos
e " são suplementares, logo:
180° − 60° ⇔
= 120°.
O triângulo
é isósceles pois os lados
e
correspondem a raios da circunferência.
Como a lados de igual comprimento se opõem ângulos de igual amplitude e como a soma das amplitudes dos
&'(°)& (°
ângulos internos de um triângulo é 180º, então: $% =
⇔ $% = 30°.
4.
a) Seja r, em centímetros, o comprimento do raio da circunferência.
De acordo com os dados,
=
= 2* e
=
= *.
Logo, +,-./0 = 2* + 2* + * + * = 6*.
Como o perímetro do retângulo é 36 cm, temos:
12
+,-./0 = 6* ⇔ 36 = 6* ⇔ * = 2 ⇔ * = 6 cm.
Logo, o comprimento da circunferência é ⊙ = 24 × 6 = 124 ≈ 37,7 centímetros.
b) Como a amplitude de um ângulo inscrito numa circunferência é metade da amplitude do arco compreendido
entre os seus lados, temos DF = 2 × DEF = 2 × 25º = 50º .
Como os ângulos DOF e AOE são verticalmente opostos os arcos correspondentes são iguais, isto é,
DF = AE = 50º .
Assim, DE = DA + AE = 180º +50º = 230º .
Logo a rotação de centro em O que transforma o ponto F no ponto A tem 230º (ou −130°) de amplitude.
c) A alternativa correta é: “O ponto O pertence à mediatriz do segmento de reta
equidistante dos extremos do segmento, visto que
=
, já que + 06+
circunferência.
”, pois o ponto O é
0 são raios da mesma
5. Vamos começar por determinar
para sabermos a amplitude do ângulo interno e do ângulo externo deste
polígono.
Sabendo que em qualquer polígono convexo a soma da amplitude de um ângulo interno com o seu ângulo
externo adjacente é 180º tem-se:
2
⇔
− 2380 +
+ 10 = 180 ⇔
−1 ± √1 + 10200
=
⇔
2
2
+
− 2550 = 0 ⇔
=
−1 ± 812 − 4 × 1 × −2550
−1 + 101
−1 − 101
=
∨ =
⇔
2
2
2×1
= 50 ∨ = −51
O ângulo interno deste polígono regular tem 50 − 2380, ou seja, 120º e o ângulo externo deste polígono
regular tem 50º + 10º, ou seja, 60º.
Usando a relação existente entre a amplitude de um ângulo externo de um polígono regular com os seus ; lados
tem-se:
12(°
12(°
= 60°, ou seja, ; = 2(° ⇔ ; = 6.
<
Conclui-se assim que este polígono regular tem 6 lados.
5
6. Vamos começar por calcular a área do setor circular da base da parte do cilindro representada:
=×>×? @
onde * 26 e = 24°.
12(
@
A×>× 2
&2 A>
2B2
Área do setor circular =
=
=
4 ≈ 141,58
12(
12(
&C
2B2
CA('
Calculando o volume do sólido representado: D = &C 4 × 8 = &C 4
Área do setor circular
3
O sólido tem 1132,6 cm de volume.
≈ 1132,6
7.
a) Como o arco AC é o correspondente ao ângulo inscrito ABC, a sua amplitude é o dobro da amplitude do ângulo
dado, ou seja, AC = 2 × 32º = 64º .
b) Os segmentos de reta AO e OE são ambos raios da mesma circunferência, pelo que têm igual comprimento, isto
é, 7,4 cm. Para determinar o comprimento do segmento de reta DE, é preciso calcular o comprimento do
segmento de reta DO. Ora DO é um dos catetos de um triângulo retângulo de que se sabe a medida da
hipotenusa e em que o comprimento do outro cateto é metade do da corda AC, ou seja, 2,4 cm. Assim, pode-se
aplicar o teorema de Pitágoras:
=
+
⇔ 7,4 =
+ 2,4 ⇔
= 7,4 − 2,4 ⇔
= 49 ⟹
= √49 ⟺
= 7.
O comprimento do segmento de reta DE é 0,4 cm, dado que 7,4 – 7 = 0,4.
8.
a) O ângulo BDC tem de amplitude 40º, visto que é um ângulo inscrito no arco BC. O ângulo DCA tem de
amplitude 55º (considerando o triângulo DCP, 180 − 85 − 40 = 55). Os ângulos DCA e DBA são ambos
ângulos inscritos no arco DA, pelo que têm a mesma amplitude.
O ângulo DBA tem 55º de amplitude.
b) Pelo enunciado, sabemos que o triângulo ABP é uma ampliação do triângulo DCP (cuja área é 24) de razão de
&
&
&
&
semelhança , portanto a razão entre as áreas será H I , ou seja, A. Então a sua área é 6 (24 × A).
9.
a) Os ângulos ao centro de um polígono regular inscrito numa circunferência são todos congruentes. Neste caso,
12(°
cada um tem 60º de amplitude, pois 2 = 60°.
Assim, J = 120° e, portanto AE = 120º (a amplitude de um ângulo ao centro é igual à amplitude do
arco compreendido entre os seus lados).
Então,
= 60° (a amplitude de um ângulo inscrito é metade da amplitude do arco compreendido entre os
seus lados).
b) O arco AE tem 120º de amplitude (podemos deduzir da alínea anterior) e a circunferência tem 6 cm de raio.
& (°× >×2
Então o K L*M 6;NKOKP* K = 12(° = 44.
c) Um hexágono regular pode ser decomposto em 6 triângulos congruentes equiláteros. Neste caso,
consideremos o triângulo equilátero AGF. Sabemos que AG = 6 cm (raio da circunferência) e que
Q = 3 cm. Calculemos JQ, usando o Teorema de Pitágoras:
JQ + 3 = 6 ⇔ JQ + 9 = 36 ⇔ JQ = 36 − 9 ⇔ JQ = 27 ⟹ JQ = √27 cm.
d) O paralelogramo AFEG pode ser decomposto em dois triângulos equiláteros dos quais conhecemos a base
(6 cm) e a altura (√27 cm). Assim a Á*6P = 2 ×
2×√ B
= 6 × √27 cm2.
e) Vamos calcular a área do hexágono, seguindo o mesmo raciocínio das alíneas anteriores:
2×√ B
= 6 × X?Yâ<V[\W = 6 ×
= 18 × √27 cm2.
Agora, calculemos a área do círculo com 6 cm de raio: ]í?][\W = 4 × 6 = 364 cm2.
Á*6P_K`M MNPOP = ]í?][\W − ST=áVW<W = 364 − 18 × √27 ≈ 20 cm2.
ST=áVW<W
f) O triângulo AGB é “equilátero” pois a base (um dos lados do hexágono) tem 6 cm e os outros dois lados são raios
da circunferência, também com 6 cm.
6