listas de recuperação – trigonometria no

Exercícios de MATEMÁTICA-Recuperação
Colégio Zaccaria
2º PERÍODO
www.zaccaria.g12.br
Valor:
5,0
Nota:
SÉRIE 21
Data:
JUNHO
Aluno(a):
Turma:
2014
N.:
Turno: Manhã
Professora: CAROLINA FRANÇA
LISTAS DE RECUPERAÇÃO – TRIGONOMETRIA NO TRIÂNGULO RETÂNGULO
– 2101 – 2º BIM
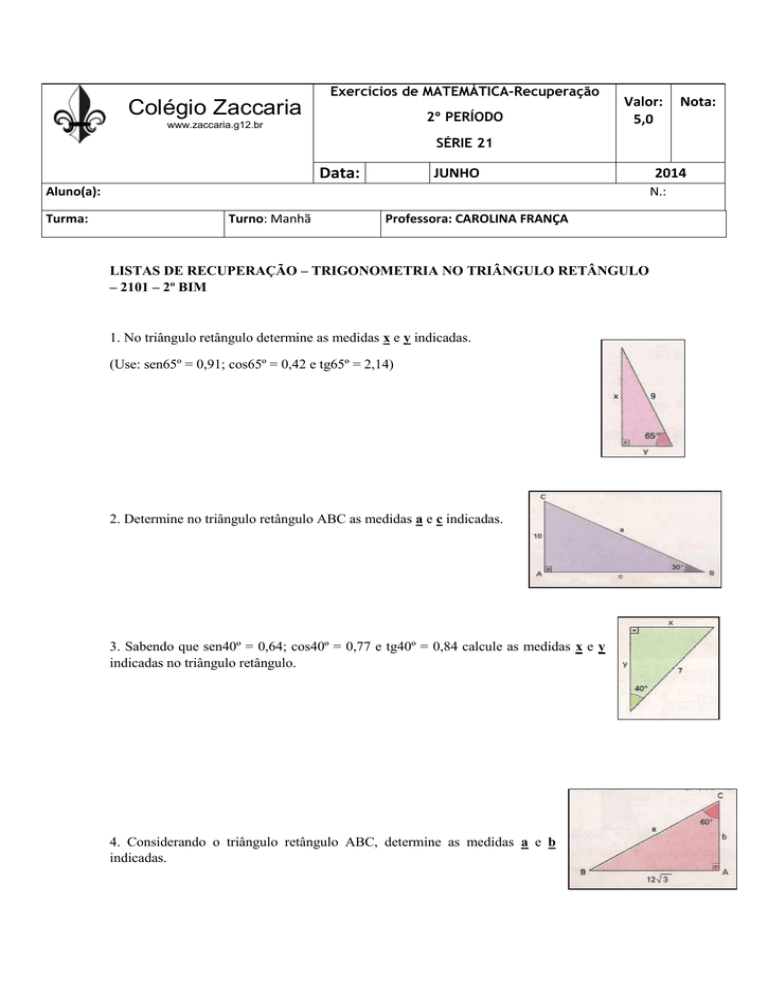
1. No triângulo retângulo determine as medidas x e y indicadas.
(Use: sen65º = 0,91; cos65º = 0,42 e tg65º = 2,14)
2. Determine no triângulo retângulo ABC as medidas a e c indicadas.
3. Sabendo que sen40º = 0,64; cos40º = 0,77 e tg40º = 0,84 calcule as medidas x e y
indicadas no triângulo retângulo.
4. Considerando o triângulo retângulo ABC, determine as medidas a e b
indicadas.
5. Em um triângulo retângulo isósceles, cada cateto mede 30cm. Determine a medida
da hipotenusa desse triângulo.
6. A diagonal de um quadrado mede 6 2 cm, conforme nos mostra a figura.
Nessas condições, qual é o perímetro desse quadrado?
7. Uma pipa é presa a um fio esticado que forma um ângulo de 45º com o
solo. O comprimento do fio é 80m. Determine a altura da pipa em
relação ao solo. Dado
2 = 1,41
8. Qual é o comprimento da sombra de uma árvore de 5 m de altura
quando o sol está 30º acima do horizonte? Dado
3 = 1,73
9. Determine a altura do prédio da figura seguinte:
10. Para determinar a altura de um edifício, um observador coloca-se
a 30m de distância e assim o observa segundo um ângulo de 30º,
conforme mostra a figura. Calcule a altura do edifício medida a partir do solo horizontal. Dado
3 = 1,73
11. Observe a figura e determine:
a) Qual é o comprimento da rampa?
b) Qual é a distância do inicio da rampa ao barranco?
12. A uma distância de 40m, uma torre é vista sob um ângulo  ,
como mostra a figura. Determine a altura h da torre se  = 30º.
13. Em um triângulo ABC, retângulo em A, o ângulo B mede 30º e a hipotenusa mede 5cm.
Determine as medidas dos catetos AC e AB desse triângulo.
14. (VUNESP) Uma pessoa, no nível do solo, observa o ponto mais alto de uma torre vertical, à
sua frente, sob o ângulo de 30º. Aproximando-se 40 metros da torre, ela passa a ver esse ponto
sob o ângulo de 45º. Calcule a altura aproximada da torre, em metros.
15. (PUCCAMP) Uma pessoa encontra-se num ponto A, localizado na base de um
prédio, conforme mostra a figura adiante. Se ela caminhar 90 metros em linha reta,
chegará a um ponto B, de onde poderá ver o topo C do prédio, sob um ângulo de 60°.
Quantos metros ela deverá se afastar do ponto A, andando em linha reta no sentido
de A para B, para que possa enxergar o topo do prédio sob um ângulo de 30°?
a) 150
b) 180
c) 270
d) 300
e) 310
16. (PUCCAMP) A figura a seguir é um corte vertical de uma peça usada em certo tipo de
máquina. No corte aparecem dois círculos, com raios de 3cm e 4cm, um
suporte vertical e um apoio horizontal. A partir das medidas indicadas na
figura, conclui-se que a altura do suporte é:
a) 7cm
b) 11cm
c) 12cm
d) 14cm
e)16 cm
17. Um observador vê um edifício, construído em terreno plano, sob um ângulo
de 60º. Se ele se afastar do edifício mais 30m, passará a vê-lo sob ângulo de
45º. Calcule a altura do edifício.
18. Determine na figura a área do triângulo BCD e a medida do segmento AD .
19. Determine as medidas dos catetos do triângulo retângulo abaixo.
A
Use : Sen 37º = 0,60
Cos 37º = 0,80
tg 37º = 0,75
x
50 cm
37º
C
B
y
20. Determine as medidas x e y indicadas no triângulo retângulo abaixo. ( dados sen 35º =
0,574
cos 35º = 0,819 )
6 cm
x
35º
y
21. Determine as medidas dos catetos do triângulo retângulo abaixo. A
x
80 cm
30º
B
y
C
22. No triângulo ABC da figura seguinte, as medidas dos lados estão em cm. Determine a
medida x da base BC.
A
60º
5
x
B
C
23. Determine as medidas dos catetos do triângulo retângulo abaixo.
A
100 cm
x
30º
B
C
y
24. No triângulo retângulo abaixo, determine o valor de x + y.
A
Use Sen 40º = 0,64 Cos 40º = 0,77
x
7 cm
40º
C
B
y
25. Calcule as medidas x e y indicadas no triângulo retângulo isósceles da figura.
C
Y
45º
60º
26. Uma escada faz um ângulo de 60° com a parede vertical de um prédio, ao tocar o topo
X
distante do 6 metros do solo. Determine o comprimento da escada.
a) 13
b) 12
c) 17
B
9 cm
A
d) 15
e) 19
27. Uma pessoa está distante 90 metros da base de um prédio e vê o seu ponto mais alto sob um
ângulo de 60°. Qual é a altura do prédio, em metros ?
a) 90 3
b) 30 3
c) 30 2
d) 90 2
e) 90 5
28. Um canhão lança um projétil a velocidade de 50 m/s com um ângulo de inclinação de 30° em
relação ao solo. Determine a altura em metros, que o projétil atingiu depois de 3s, supondo sua
trajetória retilínea e velocidade constante.
a) 76
b) 72
c) 77
d) 75
e) 79
29. Em um triângulo retângulo, a hipotenusa mede 60m e um de seus ângulos mede 30°. Qual é
o seu perímetro?
a) 50 3
b) 30 3
c) 30 2
d) 40 2
e) 90 5
30. Calcule x indicado na figura
a) 50 3
b) 30 3
c) 30 2
d) 40 2
e) 90 5
31. Na figura indicada calcule AB.
a) 73
b) 72
c) 77
d) 75
e) 79