TC de Física Nº 02 - Colégio Ari de Sá

TC DE FÍSICA – OLIMPÍADA
Professor: Ivan Peixoto
ALUNO(A):
TURMA:
Nº
TURNO:
DATA:
/
/
COLÉGIO:
OSG 2235/08
Exercícios de dinâmica retilínea
1.
(1987) Um extraterrestre faz uma experiência para determinar g em Marte, com um tipo local de máquina de Atwood.
Pendura duas massas iguais de 0,1 kg sobre uma polia sem atrito e adiciona uma outra de 0,01 kg de um lado. Depois que
o lado mais pesado desce 50 cm, a massa adicional é removida, e o sistema percorre 1,0 m nos 3,5 s seguintes. Que valor
o extraterrestre obteve para g?
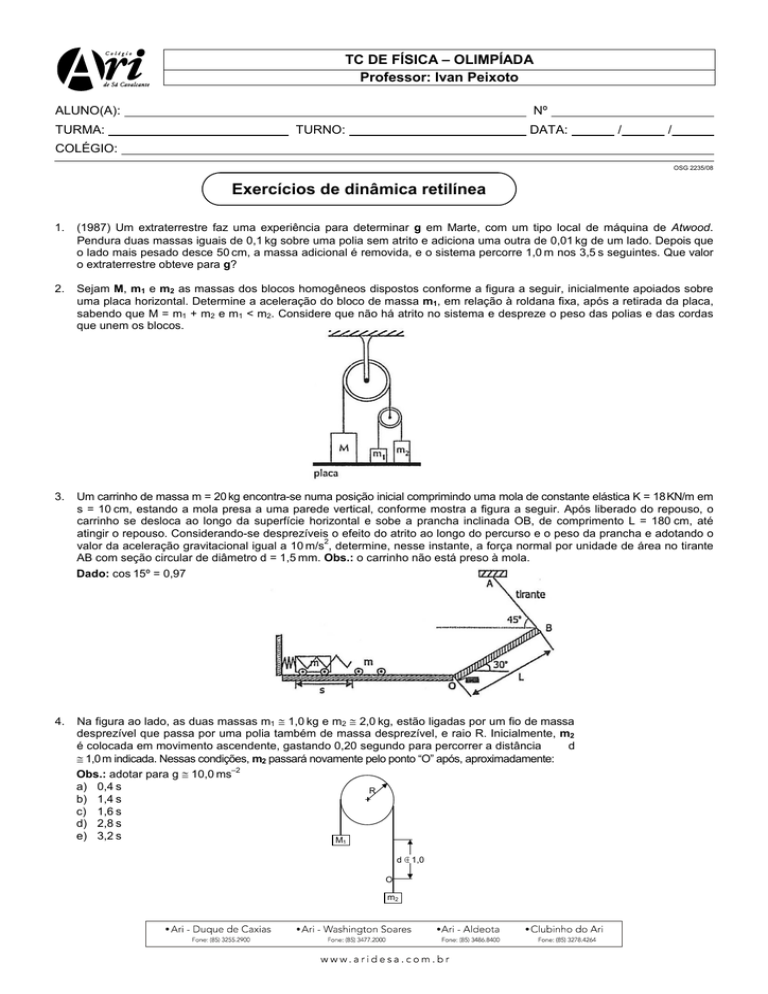
2.
Sejam M, m1 e m2 as massas dos blocos homogêneos dispostos conforme a figura a seguir, inicialmente apoiados sobre
uma placa horizontal. Determine a aceleração do bloco de massa m1, em relação à roldana fixa, após a retirada da placa,
sabendo que M = m1 + m2 e m1 < m2. Considere que não há atrito no sistema e despreze o peso das polias e das cordas
que unem os blocos.
3.
Um carrinho de massa m = 20 kg encontra-se numa posição inicial comprimindo uma mola de constante elástica K = 18 KN/m em
s = 10 cm, estando a mola presa a uma parede vertical, conforme mostra a figura a seguir. Após liberado do repouso, o
carrinho se desloca ao longo da superfície horizontal e sobe a prancha inclinada OB, de comprimento L = 180 cm, até
atingir o repouso. Considerando-se desprezíveis o efeito do atrito ao longo do percurso e o peso da prancha e adotando o
2
valor da aceleração gravitacional igual a 10 m/s , determine, nesse instante, a força normal por unidade de área no tirante
AB com seção circular de diâmetro d = 1,5 mm. Obs.: o carrinho não está preso à mola.
Dado: cos 15º = 0,97
4.
Na figura ao lado, as duas massas m1 ≅ 1,0 kg e m2 ≅ 2,0 kg, estão ligadas por um fio de massa
desprezível que passa por uma polia também de massa desprezível, e raio R. Inicialmente, m2
é colocada em movimento ascendente, gastando 0,20 segundo para percorrer a distância
d
≅ 1,0 m indicada. Nessas condições, m2 passará novamente pelo ponto “O” após, aproximadamente:
–2
Obs.: adotar para g ≅ 10,0 ms
a) 0,4 s
R
b) 1,4 s
c) 1,6 s
d) 2,8 s
e) 3,2 s
M1
d ≈ 1,0
O
m2
TC DE FÍSICA – OLIMPÍADA
5.
A figura representa um sistema mecânico com as seguintes características: r é
uma roldana de massa desprezível que pode girar sem atrito: B é um balde de
massa m, e P é um peso de massa M tal que m = 0,8 M; B e P são ligados por
uma corda apoiada em r, mas que não escorrega sobre a roldana; R é um
reservatório que contém água e uma torneira T que é adicionada quando o
balde toca nela; o balde, por sua vez, possui uma válvula que se abre em
contato com o solo permitindo a saída de toda a água; o balde cheio tem massa
mc = 1,2 M. A amplitude do movimento é h = 4,0 m. Sabendo-se que as
operações de enchimento e de esvaziamento do balde demoram tempo
∆t
= 5,0 s cada uma, e que o movimento só se processa com o balde cheio ou
vazio, calcule o período completo desse movimento periódico.
R
r
T
m
B
V
h
M
6.
P
Dois blocos de massa M estão unidos por um fio de massa desprezível que passa por uma roldana com um eixo fixo. Um
terceiro bloco de massa m é colocado suavemente sobre um dos blocos, como mostra a figura. Com que força esse
pequeno bloco de massa m pressionará o bloco sobre o qual foi colocado?
a)
b)
c)
d)
e)
2mMg
2M + m
mg
(m – M)g
mg
2M + m
Outra expressão.
7.
Um pêndulo é constituído por uma partícula de massa m suspensa por um fio de massa desprezível, flexível e inextensível,
de comprimento L. O pêndulo é solto a partir do repouso, na posição A, e desliza sem atrito ao longo de um plano de
inclinação α, como mostra a figura. Considere que o corpo abandona suavemente o plano no ponto B, após percorrer uma
distância d sobre ele. A tração no fio, no instante em que o corpo deixa o plano, é:
d
a) mg   cos α.
L
b) mg cos α.
d
c) 3mg   sen α.
L
d
d) mg   sen α.
L
e) 3 mg.
8.
No sistema, o bloco de massa M pode deslocar-se sem atrito. No instante inicial, o corpo de massa m, suspenso por um fio
ideal, determina com a vertical um ângulo α, quando é então abandonado. Determinar a massa m, em função dos
parâmetros dados, sabendo que, enquanto não sofrer uma ação externa, o ângulo α não varia.
Dados: g, M e α.
M
α
m
9.
O anel circular uniforme pesa 300 N e tem 0,45 m e diâmetro. É suportado três cabos, cada um com 0,375 m de
comprimento. Se α = 150º e β = 120º, determine a tração em cada cabo.
2
OSG 2235/08
TC DE FÍSICA – OLIMPÍADA
D
B
α
A
γ
90º
β
C
10. O bloco deslizante B parte do repouso e move-se para a direita com aceleração constante devido a um agente externo.
Não existe atrito entre as superfícies. Após T segundo B sofreu um deslocamento L. Determine a velocidade e o
deslocamento de A após decorridos nT segundos.
A
B
11. Uma força constante F atua sobre um suporte liso de massa m1. Dois corpos, de massas m2 e m3, estão suspensos por
um fio leve que passa pelo suporte, conforme está na figura. Admitindo que F seja maior que 2T, determine:
a) a aceleração de cada um dos corpos e a tensão no fio, se m1 = m2 = m3.
b) a aceleração de cada corpo, se m1 = m2 e m3 = 2m1.
r
12. Considere uma rampa de ângulo θ com a horizontal sobre a qual desce um vagão, com aceleração a , em cujo teto está
dependurada uma mola de comprimento Ρ, de massa desprezível e constante de mola k, tendo uma massa m fixada na
sua extremidade. Considerando que Ρ0 é o comprimento natural da mola e que o sistema está em repouso com relação ao
vagão, pode-se dizer que a mola sofreu uma variação de comprimento ∆Ρ = Ρ – Ρ0 dada por:
a) ∆Ρ = mg sen θ/k.
b) ∆Ρ = mg cos θ/k.
c) ∆Ρ = mg/k
d) ∆Ρ = m a2 − 2ag cos θ + g 2 / k.
e) ∆Ρ = m a2 − 2ag senθ + g 2 / k.
13. As figuras representam um plano inclinado cujo ângulo de inclinação sobre o horizonte é α. Sobre ele pode deslizar, sem
atrito, um corpo de massa M. O contrapeso tem massa m, e uma das extremidades do fio está fixa ao solo. Na figura (B) o
plano inclinado foi suspenso, de modo a se poder ligar às massas m e M por meio de outro fio.
OSG 2235/08
3
TC DE FÍSICA – OLIMPÍADA
Desprezando os atritos nos suportes dos fios, desprezando a massa dos fios e sendo dada a aceleração da gravidade g,
podemos afirmar que:
a) no caos (A), a posição de equilíbrio estático do sistema ocorre se, e somente se, M sen α = m.
b) tanto no caso (A) como no caso (B), o equilíbrio se estabelece quando, e somente quando, M = m.
c) no caso (B), o corpo m é tracionado em A por uma força TA = (m + M sen α)g.
d) no caso (B), a aceleração do corpo M é g(M sen α – m) / (M + m) no sentido descendente.
e) no caso (A), não há nenhuma posição possível de equilíbrio estático.
14. Um bloco de 4,0 kg é colocado sobre outro de 5,0 kg. Mantendo-se o bloco inferior fixo, para fazer o bloco de cima
escorregar sobre o bloco inferior, é necessário aplicar uma força horizontal de 15 N sobre o bloco superior. Os blocos são
agora colocados sobre uma horizontal sem atrito, conforme indicado na figura. Determine:
2
Dado: g = 10 m/s .
a) a força F horizontal máxima que pode ser aplicada ao bloco inferior para que os blocos se movam permanecendo juntos;
b) a aceleração do sistema.
15. Um pára-quedista de massa m ao saltar de pára-quedas atinge uma velocidade v1 de equilíbrio. Um outro pára-quedista,
com metade de sua massa, atinge uma velocidade v2, também no equilíbrio. Sabendo-se que a força de resistência do ar é
proporcional ao quadrado da velocidade, calcule a relação entre v1 e v2.
Exercícios de de atrito
1.
2.
Um antigo vaso chinês está a uma distância d da extremidade de um forro sobre uma mesa. Essa extremidade, por sua
vez, se encontra a uma distância D de uma das bordas da mesa, como mostrado na figura. Inicialmente tudo está em
repouso. Você apostou que consegue puxar o forro com uma aceleração constante a (veja figura), de tal forma que o vaso
não caia da mesa. Considere que ambos os coeficientes de atrito, estático e cinético, entre o vaso e o forro tenham o valor
µ e que o vaso pare no momento que toca a mesa. Você ganhará a aposta se a magnitude da aceleração estiver dentro da
faixa:
d
a) a <
µg
D
d
b) a >
µg
D
c) a > µg
D
d) a > µg
d
D
e) a >
µg
D −d
r
Na figura, o carrinho com rampa movimenta-se com uma aceleração constante A . Sobre a rampa repousa um bloco de
r
massa m. Se µ é o coeficiente de atrito estático entre o bloco e a rampa, determine o intervalo de A , no qual o bloco
permanecerá em repouso sobre a rampa.
4
OSG 2235/08
TC DE FÍSICA – OLIMPÍADA
3.
Um atleta mantém-se suspenso em equilíbrio, forçando as mãos contra duas paredes verticais, perpendiculares entre si,
dispondo seu corpo simetricamente em relação ao canto e mantendo seus braços horizontalmente alinhados, como mostra
a figura. Sendo m a massa do corpo do atleta e µ o coeficiente de atrito estático interveniente, assinale a opção correta
que indica o módulo mínimo da força exercida pelo atleta em cada parede.
1/ 2
a)
mg  µ2 − 1 


2  µ2 + 1
b)
mg  µ2 + 1 


2  µ2 − 1 
c)
mg  µ2 − 1 


2  µ 2 + 1
d)
mg  µ2 + 1


2  µ2 − 1
1/ 2
e) n.d.a.
4.
A figura representa uma mesa horizontal de coeficiente de atrito cinético µ1, sobre a qual se apóia o bloco de massa M2.
Sobre ele está apoiado o objeto de massa m, sendo µ o coeficiente de atrito cinético entre eles. M2 e m estão ligados por
cabos horizontais esticados, de massa desprezível, que passam por uma roldana de massa também desprezível.
Desprezando-se a resistência do ar e o atrito nas roldanas, podemos afirmar que m se deslocará com velocidade constante
em relação a um observador fixo na mesa se M1 for tal que:
a) M1 = µm
b) M1 = µ1(M2 + m) + 2 µm
c) M1 = µ1M2 + µm
d) M1 = 2 µm + 2µ1 (M2 + m)
e) M1 = µ1 (M2 + m)
5.
O cachorrinho da figura tem massa 10 kg e move-se num terreno horizontal numa trajetória de raio de curvatura 1,0 m.
Num dado instante, sua velocidade é de 0,36 km/h e ele exerce contra o solo forças de 0,10 N (dirigida de A para o centro
de curvatura C) e de 0,050 N (tangencial). Sabendo que a mão do dono está na vertical erguida do centro de curvatura,
podemos afirmar que a tensão na guia e a aceleração tangencial do cachorrinho valem, respectivamente:
–3
–2
I. zero e 5,0 x 10 ms
–3
–2
II. 0,23 N e 5,0 x 10 ms
–3
–2
III. 196 N e 5,0 x 10 ms
–2
IV. 0,11 N e 0,01 ms
–2
V. 0,23 N e 0,01 ms
6.
Um motoqueiro efetua uma curva de raio de curvatura de 80 m a 20 m/s num plano horizontal. A massa total (motoqueiro + moto) é
de 100 kg. Se o coeficiente de atrito estático entre o pavimento e o pneu da moto vale 0,6, podemos afirmar que: a máxima
força de atrito estático fa e a tangente trigonométrica do ângulo de inclinação θ, da moto em relação à vertical, serão
dados, respectivamente, por:
fa(N)
a) 500
b) 600
c) 500
7.
tgθ
0,5
0,5
0,6
d)
e)
fa(N)
600
500
tgθ
0,6
0,3
A figura ao lado representa três blocos de massas M1 = 1,00 kg, M2 = 2,50 kg e M3 = 0,50 kg, respectivamente. Entre os
blocos e o piso que os apóia existe atrito, cujos coeficientes cinético e estático são, respectivamente, 0,10 e 0,15, e a
2
aceleração da gravidade vale 10,0 m/s . Se ao bloco M1 for aplicada uma força F horizontal de 10,00 N, pode-se afirmar
que a força que o bloco 2 aplica sobre o bloco 3 vale:
a) 0,25 N.
OSG 2235/08
5
TC DE FÍSICA – OLIMPÍADA
b)
c)
d)
e)
10,00 N.
2,86 N.
1,25 N.
Nenhuma das anteriores.
8.
Um motociclista trafega numa estrada reta e nivelada atrás de um caminhão de 4,00 m de largura, perpendicularmente à
carroceria. Ambos estão trafegando à velocidade constante de 72 km/h quando o caminhão se detém instantaneamente,
devido a uma colisão. Se o tempo de reação do motociclista for 0,50 s, a que distância mínima ele deverá estar trafegando
para evitar o choque apenas com mudança de trajetória? Considere o coeficiente de atrito entre o pneumático e o solo µ =
2
0,80, aceleração gravitacional g = 10,0 m/s e que a trajetória original o levaria a colidir-se no meio da carroceria.
d) 24,0 m
a) 19,6 m
b) 79,3 m
e) 14,0 m
c) 69,3 m
9.
Considere o veículo de massa M percorrendo uma curva inclinada, de ângulo θ, com raio R constante, a uma velocidade V.
Supondo que o coeficiente de atrito dos pneus com o solo seja µ, calcule as velocidades mínima e máxima com que esse
veículo pode percorrer essa curva, sem deslizamento.
10. Um pequeno bloco de massa m é lançado ladeira acima ao longo de uma rampa que forma um ângulo α com a horizontal.
Determine o coeficiente de atrito µ, sabendo que o tempo de subida do bloco é n vezes menor que o seu tempo de
descida.
11. Na figura, o corpo de massa m2 = 10 kg escorrega sobre uma mesa sem atrito. Os coeficientes de atrito estático e cinético
entre m2 e m1 = 5 kg são µe = 0,6 e µc = 0,4. Calcule:
a) Qual é a aceleração máxima de m1?
b) Qual é o valor máximo de m3 quando m1 desloca-se, sem escorregar, com m2?
c) Se m3 = 30 kg, determine a aceleração de cada massa e a tensão no cabo.
12. Um bloquinho de massa igual a m repousa sobre a extremidade de uma prancha de comprimento L e massa M, como
mostra a figura abaixo. Os coeficientes de atrito estático e cinético entre o bloquinho e a prancha valem µe e µc. Se a
gravidade local vale g, determine:
a) qual o maior valor da força horizontal F com que se pode puxar a prancha sem que o bloquinho escorregue em relação
a ela?
b) supondo que esse limite da força F tenha sido ultrapassado, quanto tempo levará para que o bloquinho caia da
extremidade da prancha?
13. Uma força horizontal F = 80 N está empurrando um bloco de massa m = 6 kg contra uma parede
2
vertical, conforme indicado na figura (g = 10 m/s ). O coeficiente de atrito estático entre a parede e o
bloco vale 0,8, e o coeficiente de atrito cinético vale 0,6. Suponha que, inicialmente, o bloco esteja em
F
repouso.
a) Com a força F aplicada, o corpo começará a se mover?
b) Qual é nesse caso a força exercida pela parede sobre o bloco?
c) Qual seria o valor de F máximo necessário para começar o movimento?
d) Determine o valor de F necessário para que o corpo escorregue contra a parede com velocidade constante.
2
e) Obtenha o valor de F para que o bloco escorregue contra a parede com uma aceleração igual a 4 m/s .
14. Observe a figura. Um bloco de massa m escorrega sobre a calha, que forma um ângulo de 90º, conforme indicado. O
coeficiente de atrito cinético entre o bloco e a calha vale µc. Determine a aceleração do bloco.
90º
θ
6
OSG 2235/08
TC DE FÍSICA – OLIMPÍADA
15. Observe a figura. Considere m1 = 10 kg, m2 = 20 kg, θ = 37º. O coeficiente de atrito cinético entre
m1 e o plano vale µ1 = 0,15 e o coeficiente correspondente a m2 vale µ2 = 0,20. A barra que liga
2
os dois blocos possui massa desprezível. (g = 10 m/s , sen37º = 0,6). Determine:
a) a força que a barra aplica no bloco 1, indicando a sua direção e sentido;
b) a aceleração comum do sistema;
c) a reação total exercida pelo plano sobre o bloco de massa m1.
d) Se você inverter as posições das massas m1 e m2, as respostas dos itens (a) e (b) se alteram?
m1
m2
0
16. A figura mostra dois blocos de mesma massa m conectados entre si através de um fio que passa por uma polia, ambos
ideais. Se a gravidade local vale g e o coeficiente de atrito entre o bloco e o carro vale µ > 1, determine a maior aceleração
a com que o carro pode se mover sem que o bloco escorregue em relação a ele.
m
α
a
m
2
17. Um corpo de M = 100 kg se desloca sobre um solo liso pela ação de uma força F com aceleração a = 6 m/s em relação à
2
terra. Um bloquinho de massa m = 20 kg abandonado sobre esse corpo também se move com aceleração 4 m/s em
relação à terra. (Portanto, esse bloquinho escorrega para trás, em relação ao corpo.)
m
Superfície lisa
a)
b)
c)
d)
M
a2 = 4 m/s2
a1 = 6 m/s2
F
Qual é a força de atrito exercida pelo corpo de 100 kg sobre o de 20 kg?
Qual a força resultante sobre o corpo de 100 kg? Qual é a força F?
Qual o coeficiente de atrito cinético entre o bloco e o corpo?
Depois de o corpo de 20 kg ter caído do de 100 kg, qual é a aceleração do corpo de 100 kg?
18. Um corpo de massa M igual a 2 kg é abandonado de uma certa altura de um plano inclinado e atinge uma mola ideal de
constante elástica igual a 900 N/m, deformando-a de 10 cm. Entre os pontos A e B, separados 0,50 m, existe atrito cujo
coeficiente vale 0,10. As outras regiões não possuem atrito. A que distância A o corpo M irá parar?
A
B
19. O esquema representa corpos A, B e C de mesma massa e o coeficiente de atrito entre B e o solo vale k. Os corpos B e C
são ligados por um cabo inextensível de massa desprezível e que passa por uma roldana ideal. Determine a máxima
aceleração para a direita que pode ter o carro A, com a condição de B permanecer em repouso.
20. O esquema representa um automóvel de massa m. O coeficiente de atrito entre as rodas e a pavimentação é µ. A pista é
reta e horizontal. O atrito de rolamento é desprezado. Determinar a maior aceleração, α, do veículo na partida, nas
seguintes hipóteses:
a) Só existe tração traseira.
b) Só existe tração dianteira.
c) Existe tração nas quatro rodas.
21. Um bloco de massa m encontra-se sobre uma tábua de massa M e comprimento Ρ que repousa sobre uma superfície
horizontal. Despreze o atrito entre a tábua e a superfície e considere que existe atrito entre o bloco e a tábua, com
OSG 2235/08
7
TC DE FÍSICA – OLIMPÍADA
coeficientes de atrito estático e cinético, respectivamente iguais a µe e µc. Em um determinado instante é aplicada uma
força horizontal F, sobre a tábua, conforme mostra a figura 1.
m
M
F
Ρ
a) Qual deve ser o valor de F para que o bloco comece a deslizar sobre a tábua?
b) Encontre o tempo t que o bloco levará para cair da tábua.
OAO.17408/Rev.: Filipe
8
OSG 2235/08