Segunda Lista

Física 2, Engenharia Elétrica, Turma E3
Lista 002 – 21/03/2006
14.1♦
♦ – Fazendo um biscate, você foi solicitado a transportar uma barra de ferro de 85,8 cm
de comprimento e 2,85 cm de diâmetro de um depósito até um mecânico. Você precisará
usar um carrinho de mão? (para responder, calcule o peso da barra).
14.2♦ – A Lua possui massa de 7,35 ×10 22 kg e raio igual a 1740 km. Qual a sua densidade
média?
14.5♦– Um barril contém uma camada de óleo de 0,120 m flutuando sobre água com uma
profundidade igual a 0,250 m. A densidade do óleo é igual a 600 kg/m3. a) Qual é a pressão
manométrica na interface entre o óleo e a água? b) Qual é a pressão manométrica no fundo
do barril?
14.6♦ – Um veículo esportivo vazio pesa 16,5 kN. Cada pneu possui uma pressão
manométrica igual a 205 kPa. a) Qual é a área total de contato dos quatro pneus com o
pavimento? (Suponha que as paredes dos pneus sejam flexíveis de modo que a pressão
exercida pelo pneu sobre o pavimento seja igual à pressão do ar existente no interior do
pneu). b) Qual é a área total, considerando a mesma
pressão manométrica do pneu, quando o peso total dos
passageiros for igual a 9,1 kN ?
14.8♦ – Qual deve ser a pressão manométrica
desenvolvida por uma bomba para bombear água do
fundo do Grand Canyon (a uma altura de 730 m) até o
Indian Gardens (a 1370 m)? Expresse sua a resposta em
pascals e em atmosferas.
14.11♦ – Um curto-circuito elétrico impede fornecimento
da potência necessária para um submarino que está a uma
profundidade de 30 m abaixo da superfície do oceano. A
tripulação deve empurrar uma escotilha com área de 0,75
m2 e peso de 300 N para poder escapar do fundo do
submarino. Se a pressão interna for igual a 1,0 atm, qual
é a força para baixo que eles devem exercer para abrir a
escotilha?
14.16♦ – Um bloco de gelo flutua sobre um lago de água
doce. Qual deve ser o volume mínimo do bloco para que
uma mulher de 45,0 kg possa ficar de pé sobre o bloco
sem que ela molhe os pés? (ρgelo=0,92 ρágua).
14.25♦ – A película da Figura 14.14 refere-se à solução
de água e sabão indicada na Tabela 14.2 (a 20oC tensão
superficial de 25 dyn/cm ou mN/m). Ela possui 22,0 cm
de largura e está a 20oC. O fio que desliza possui massa
igual a 0,700 g. Qual é o módulo necessário T da força
que puxa para baixo, para manter o fio em equilíbrio?
14.26♦ – A água escoa em um tubo cuja secção reta possui área variável e em todos os
pontos a água enche completamente o tubo. No ponto 1 a secção reta possui área igual a
0,700 m2 e o módulo da velocidade do fluido é igual a 3,50 m/s. a) Qual é a velocidade do
fluido nos pontos para os quais a secção reta possui área igual a (i) = 0,105 m2 ? (ii) 0,047
m2 ? (b) Calcule o volume da água descarregada pela extremidade aberta do tubo em 1 hora.
14.29♦ – Um tanque selado que contém água do mar até uma altura igual a 11,0 m.
Também contém ar acima da água a uma pressão manométrica igual a 3,00 atm. A água flui
para fora através de um pequeno orifício na base do tanque. Calcule a velocidade de efluxo
da água.
14.33♦ – Sustentação de um avião. As linhas de corrente horizontais em torno das pequenas
asas de um avião são tais que a velocidade sobre a superfície superior é igual a 70,0 m/s e
sobre a superfície inferior é igual a 60,0 m/s. Se o avião possui massa igual a 1340 kg e a
área da asa é igual a 16,2 m2, qual é a força resultante vertical (incluindo o efeito da
gravidade) sobre ao avião? A densidade do ar é igual a 1,20 kg/m3.
14.37♦ – Água a 20oC se escoa em tubo de raio igual a 10,0 cm. A viscosidade da água é
igual a 1,005 centipoise. Se a velocidade da água no centro do tubo é igual a 2,50 m/s, qual
é a velocidade da água (a) a 5,0 cm a partir do centro do tubo (na metade do caminho entre
o centro e a parede)? (b) sobre as paredes do tubo?
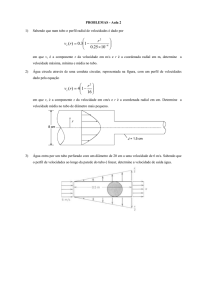
Q7♣ – Coloca-se água a um mesmo nível em todos os recipientes mostrados na Figura 7. As
áreas das bases são idênticas para todos os
recipientes. Se a pressão nas partes inferiores de
todos os recipientes são idênticas, a força suportada
pela base de cada recipiente é a mesma. Por que,
então, os três recipientes possuem diferentes pesos
quando colocados sobre uma balança? Este resultado
Figura 7
é conhecido como o paradoxo hidrostático.
E29♣ – Três crianças, cada uma pesando 82,4 lb, constroem uma jangada unindo toras de madeira
com 1,05 ft de diâmetro e 5,80 ft de comprimento. Quantas toras são necessárias para mantê-las
flutuando? Considere a massa específica da madeira sendo de 47,3 lb/ft2?
P12♣ – (a) Um fluido gira em com velocidade angular constante ω em relação ao eixo móvel
vertical central de um reservatório cilíndrico. Mostre que a variação da pressão na direção radial é
dp
= ρ ω 2r .
expressa por
dr
(b) Faça p = pc no eixo de rotação (r =0) e mostre que a velocidade p em um ponto qualquer a uma
1
distância r vale p = pc + ρ ω 2 r .
2
(c) Mostre que a superfície do líquido possui a forma de um parabolóide de revolução, isto é, uma
secção transversal vertical da superfície pode ser representada pela curva y = ω 2 r 2 / 2 g .
(d) Mostre que a variação da pressão com a profundidade é p = ρ g h .
E1♠ – Uma tubulação com 34,5 cm de diâmetro transporta água a 2,63 m/s. Quanto tempo será
necessário para que 1600 m2 de água sejam descarregados por esta tubulação?
E4♠ – Água é bombeada continuamente para fora de um porão inundado à velocidade de 5,30 m/s
através de uma mangueira uniforme cujo raio é de 9,70 mm. A mangueira passa através de uma
janela que se encontra a 2,90 m acima do nível da água. Qual a potência fornecida pela bomba?
E28♠ – Calcule a viscosidade máxima com a qual o sangue, a 37o, pode fluir por uma artéria com
3,8 mm de diâmetro, de modo que o escoamento seja laminar.
Exercícios do Livro Física II – Sears e Zemansky.
Exercícios do Livro Física 2 – Halliday, Resnick e Krane, capítulo 15.
♠
Exercícios do Livro Física 2 – Halliday, Resnick e Krane, capítulo 16.
♦
♣
1/2
2/2