Descarregar artigo

I — A CONDUTIBILIDADE COMO FENÓMENO
DE TRANSPORTE NA FASE LÍQUIDA
A condutibilidade iónica é um dos vários parâmetros
translacionais que podem usar-se para caracterizar o
movimento molecular num sistema líquido. Como tal,
figuram também, entre outros, a viscosidade, as condubitilidades térmica e acústica e o coeficiente de difusão, para citar só os que têm sido mais intensamente
estudados.
CONDUTIBILIDADE IONICA.
REVISÃO DOS MODELOS
E DA SUA APLICAÇÃO
F. BARREIRA
Núcleo de Química-Fisica
Comissão de Estudos de Energia Nuclear (1. A. C.)
Faculdade de Ciências
Lisboa
Consideram-se os trés modelos principais utilizados para a descrição da condutibilidade iónica — o hidrodinâmico, o ciné.ico
e o estatístico. Analisam-se os fundamentos de cada um e discute-se a respectiva aplicação, em particular no que respeita à
variação da condutibilidade com a concentração. Discute-se
ainda a possibilidade da sua verificação experimental.
Rev. Port. Quico.. 8. 19, (1966)
A condutibilidade iónica destaca-se pelo facto de poder
ser avaliada experimentalmente com muito maior precisão, traduzindo assim melhor as particularidades do
processo translacional, o que é extremamente importante quando se pretendem sujeitar os modelos propostos à verificação experimental. Cite-se já como desvantagem a circunstância de a condutibilidade iónica,
tal como é determinada experimentalmente, reflectir o
comportamento do complexo ião-solvente, em lugar do
comportamento do solvente puro.
Só quando se encontram eliminados todos os efeitos
devidos às substâncias iónicas dissolvidas é possível utilizar este parâmetro na descrição das propriedades intrínsecas do solvente.
Por isso, no estudo da condutibilidade iónica, se distinguem dois aspectos que, formalmente pelo menos,
têm sido tratados separadamente.
Têm sido estudadas as consequências da presença dos
iões na solução, a qual dá origem à formação do complexo ião-solvente e a acções interiónicas, que é necessário eliminar para que possa ser considerado o aspecto
essencial do problema que consiste na tentativa de
exprimir a condutibilidade iónica em termos de parâmetros característicos do dissolvente.
Este objectivo enquadra-se no plano mais geral da tradução do mecanismo dos fenómenos de transporte, em
função das características fundamentais dos líquidos
em que se processam. Ao contrário dos outros fenómenos de transporte, atrás mencionados, esse objectivo
só pode, no caso particular da condutibilidade, ser conseguido desde que se extrapolem para diluição infinita
os resultados obtidos com as soluções em estudo, onde
os efeitos ião-solvente e interiónicos estão sempre presentes.
Para tal, é necessário estar na posse de meios que permitam realizar essa extrapolação, ou seja, do conhecimento da lei que rege a variação da condutibilidade
com a concentração.
19
F. BARREIRA
2
—
VARIAÇÃO DA CONDUTIBILIDADE COM A
CONCENTRAÇÃO
A primeira tentativa feita no sentido de traduzir quantitativamente a variação da condutibilidade equivalente
com a concentração deve-se a ARRHENIUS (1), que propôs
um método para a determinação do grau de dissociação
baseado na equação, bem conhecida,
=
A
Ao
ARRHENIUS admitia implicitamente que o aumento verificado na condutibilidade equivalente, quando a concentração diminui, estava condicionado iìnicamente ao
aumento do número de iões, em conformidade com a
variação do grau de dissociação. A aceitação desta
equação implica automaticamente a aceitação da hipótese de as mobilidades iónicas não se alterarem quando
a concentração se modifica, o que corresponde à ausência de quaisquer efeitos de carácter interiónico.
As ideias simplificadas de ARRHENIUS tiveram de ser
abandonadas na medida em que a experiência mostrou
que a condutibilidade equivalente aumentava quando
a concentração diminuía, mesmo em circunstância tais
que o grau de dissociação não pudesse deixar de ser
tomado como igual à unidade ( 1 ).
Fica assim provada a necessidade de serem considerados
efeitos interiónicos, dependentes da concentração.
Todas as teorias propostas até hoje para a análise quantitativa destes efeitos têm como base a apresentada por
ONSAGER (3) que, pela primeira vez, tomou em consideração as consequências dos efeitos interiónicos, agrupando-os em duas categorias: o efeito electroforético
e o efeito de relaxação.
No efeito electroforético juntam-se todos os fenómenos
que resultam do facto de os iões se moverem em meio
viscoso e, portanto, arrastarem consigo parte da solução
existente na sua vizinhança. Consequentemente, os iões
vizinhos têm os seus movimentos, num solvente não
estacionário, mas que se move no mesmo sentido ou
em sentido oposto, consoante os sinais das respectivas
cargas. Este efeito é claramente dependente da concentração, atenuando-se quando a concentração diminui.
Para o seu cálculo é necessário utilizar funções de distribuição, visto estarem envolvidas distâncias entre iões.
No desenvolvimento quantitativo da teoria de ONSAGER
recorreu-se à distribuição de Boltzman, o que, aliás, foi
mantido nos ajustamentos posteriores.
No efeito de relaxação agrupam-se, por seu turno, as
acções que resultam da alteração provocada no arranjo
dos iões (com simetria esférica) em consequência da
aplicação do campo eléctrico. A dissimetria criada exerce
nos iões uma força em direcção oposta à que resulta
do campo eléctrico aplicado, tendo como consequência
directa a diminuição da mobilidade.
Assim, de acordo com estas ideias, a velocidade dos
iões numa solução de concentração não nula resultará
de quatro tipos de acções:
i)
ii)
iii)
iv)
Acção do campo eléctrico aplicado
Resultado do movimento dos iões num meio viscoso
Resultante do efeito electroforético
Resultante do efeito de relaxação.
As duas primeiras estão presentes numa solução infinitamente diluída, que pode ser visualizada como constituída por um único ião contido em quantidade infinita de solvente. Os dois últimos grupos de acções
só existem em soluções de concentração não nula.
Podemos, pois, decompor a condutibilidade iónica equivalente em três parcelas:
x = x o — >r — ^rt
onde X. se refere à condutibilidade equivalente limite
para diluição infinita, englobando as acções (i) e (ii).
x r ao efeito electroforético e x 11 ao efeito de relaxação.
As parcelas x l e x 11 são, evidentemente, subtractivas na
medida em que os efeitos que lhes correspondem aparecem como reacção ao movimento dos iões provocado
pela acção do campo eléctrico aplicado.
A independência dos efeitos está implícita na forma
corno se escreveu a expressão anterior, havendo correspondência entre os termos e os efeitos e ausência de
qualquer termo que corresponda à combinação de efeitos. Este critério tem sido repetidamente utilizado, porquanto a consideração de acções múltiplas conduz a a
expressões extremamente complicadas e de difícil manejo para comparação com os dados experimentais,
(
1)
A dificuldade na utilização de expressões mais rigorosas,
em certos problemas de aplicação, está bem patente no recurso
que ainda hoje se faz à equação de Arrhenius para a determinação
do grau de dissociação quando se não pretende rigor muito
elevado. Num trabalho recente (2), a equação de Arrhenius
foi utilizada para a verificação da lei seguida na dissociação
do ácido pícrico.
Rev. Port. Quím., 8, 19, (1966)
20
^,^..,.,^.^^...
CONDUTIBILIDADE TÓNICA
sendo muito pequeno, por outro lado, o aumento de
No caso dos electrólitos uni-univalentes, O e a têm os
precisão obtido na descrição do fenómeno em causa.
valores, respectivamente, de:
De resto, há necessidade de introduzir muitas outras
aproximações para a realização do cálculo, as quais
8,204 x 10 582,46
e=
—
ultrapassam em grandeza as que se referem á supressão
(D T) 3 / 2
^1(DT)li2
das acções múltiplas.
Na resolução do problema tal como ele se encontra
Esta expressão, tal corno foi deduzida, contém as seformulado, trata-se, por agora, de avaliar as parcelas
guintes limitações:
subtractivas a l e A„ a juntar à condutibilidade equivalente a diluição infinita, para se obter o seu valor
(i) Desprezou-se a acção do efeito de relaxação sobre
numa solução de concentração não nula.
o efeito electroforético. No cálculo do efeito elecNão há aparentemente necessidade, nesta fase, de fazer
troforético considerou-se só a acção do campo
qualquer escolha relativamente aos modelos a que reeléctrico externo, desprezando-se o campo eléctrico,
corremos para a descrição da condutibilidade equivadevido ao efeito de relaxação, que, de resto, se
lente limite, ou seja da parcela A o .
sabe ser muito menos importante.
Acontece, porém, que no cálculo do efeito electrofo(ii) Aceitou-se que o electrólito está totalmente dissorético se admite que a equação de Stokes é aplicável,
ciado, o que só é rigorosamente válido para eleco que corresponde a aceitar um modelo hidrodinâmico,
trólitos fortes em solução diluída.
ou seja um modelo segundo o qual o ião se move num
(iii) Fez-se intervir a distribuição de Holtzman para os
meio contínuo onde o movimento browniano não iniões, mas no cálculo só foi considerado o primeiro
tervém. Esta aceitação implica já urna tornada de potermo do desenvolvimento em série da exponensição relativamente ao modelo que virá servir para
cial. A convergência da série só é satisfatória para
descrever a condutibilidade equivalente em diluição inelectrólitos uni-univalentes em dissolventes de elefinita, ou seja para o cálculo de A. em função de parâvada constante dieléctrica.
metros primários característicos. Concluiremos mais
(iv) Toma-se o produto xa como suficientemente peadiante pela inadequacidade de tal modelo para a interqueno para poder ser desprezado em presença da
pretação de A ° , mas teremos de o utilizar como o único
unidade. Isto só é válido para soluções muito dipraticável para a descrição dos efeitos electroforético
luídas (rigorosamente a diluição infinita) ou para
e de relaxação. O recurso a ele e às suas consequências
iões pontuais.
tem-se mantido sempre que se trate de traduzir quantitativamente os efeitos da concentração na condutibiNo caso de electrólitos uni-univalentes, esta última é a
lidade equivalente ou em grandezas dela derivadas ( 1 ).
aproximação mais importante. Na água um cálculo
Note-se desde já que o modelo hidrodinâmico, apesar
simples permite estabelecer o limite da sua validade:
de urna formulação não aceitável, conduz a resultados
que são aproximadamente válidos.
_
_
/4
r8ó
I
0,3 x 108 V I cm' (a 25°C)
O cálculo das parcelas a l e A 11 , nesta base, dá, segundo
T
x `
k
o método proposto por ONSAGER e Fuoss (4) e recorrendo
a certas aproximações, os seguintes resultados:
Tomando para valor médio do diâmetro iónico 3-5 x
x 10 -8 cm, fàcilmente se vê que o produto xa é apro1
F 2 I z Í
zl z2 eo
qx
e 1. 11 --1`o
ximadamente igual à raiz quadrada da força iónica.
N
3DkT 1+1/q—
Se a força iónica for igual a 10 -3 , o produto xa toma
um valor próximo de 0,03. Quando se despreza, em
1 01 + 1`02
face da unidade, comete-se um erro de cerca de 3 %,
com
q = z1 I+ I z2I
I z2 I A01 + z l I 02
que é muito superior ao erro que afecta as determinações experimentais. A concentração l0 -3 moles dm -3 ,
como x é proporcional a ✓c , fàcilmente se obtém, por
conveniente agrupamento dos termos, a equação:
(I) Referir-nos-emos mais adiante a um tratamento do problema,
I
;
I ^I
), = ao — (9 A.
Rev. Port. Quírn.,
8,
19, (1966)
I
+ a)
✓C
)
que, embora utilizando o formalismo do modelo do estado de
transição, faz também depender a condutibilidade da viscosidade.
21
F BARREIRA
para elctrólitos uni-univalentes, constitui o limite superior para a validade da equação deduzida, no caso da
água, a 25°C. No caso de valências mais elevadas, o
ajustamento é ainda mais difícil, como se vê fácilmente
pela expressão da força iónica.
A exaustiva verificação experimental da validade da
equação obtida a partir da teoria de Onsager tem sido
praticada, especialmente em soluções aquosas, e mostrou
que, nas condições em que foi estabelecida a equação,
é válida.
Já KOHLRAUSCH havia obtido empiricamente urna equação da mesma forma, sem, no entanto, ter podido
prever o valor dos coeficientes do termo independente
e do termo em c 1 / 2 .
Para soluções mais concentradas, dado que esta equação
não é válida, e para resolver o problema do cálculo
da condutibilidade equivalente a diluição infinita (que
é a grandeza fundamental) têm sido propostas várias
equações com base mais ou menos empírica. Dentre
elas, e como exemplo, citamos a de SHEDLOVSKY (5).
O método de determinação de A. implica o cálculo
da quantidade
_
a+aVc
1 —e e
que varia linearmente com a concentração. A extrapolação para c=o fornece a° . Esta equação é aplicável
para concentrações até 0,! M. O método de extrapolação corresponde a escrever
a = a°
—
(0).° + a) e 112 — Bc — O B c 3 / 2
ou seja a introduzir, de forma empírica, termos em
ce e 312 .
A constância do coeficiente B pode ser justificada em
termos da teoria completa e resulta de consequências
fortuitas de valores numéricos particulares.
A simples necessidade de se recorrer a equações empíricas mostra bem até que ponto se devem limitar as
aproximações a introduzir na dedução das equações
que traduzem a variação da condutibilidade equivalente com a concentração.
Com fundamento teórico, foram propostas outras expressões, de que se destaca a de FALKENHAGEN (6)
a=a gi (6a° + a) c 112 +aBa+ea+ 1,707 a0 aBe)c-
- 2,707 a B O a e 312
onde aparece já explicitamente o parâmetro a, diâmetro
médio dos iões.
22
Houve uma alteração importante em relação ao tratamento de Onsager e Fuoss. Passou-se de um modelo
em que o ião (em solução concentrada) é tomado como
pontual para outro em que é agora considerado como
uma esfera rígida, com dimensões. Por outro lado, foi
tido em conta o campo eléctrico devido à relaxação,
no cálculo do efeito electroforético.
Fuoss e ONSAGER (7) retomaram o assunto da variação
da condutibilidade com a concentração, retendo, nos
desenvolvimentos em série, termos de ordem superior
a c 112 e considerando o ião com dimensões. Obtiveram
a expressão
a=a°
—
(6a„+a) c 112 + Jc+Ec log c
onde J é função do parâmetro a.
Voltaram, recentemente (8), a preocupar-se com este
problema, utilizando forma diferente para a expressão
das forças totais dirigidas que actuam nos iões, o que
lhes permitiu fazer a respectiva integração com o factor
de Boltzman em forma exponencial, obtendo, por fim,
a equação:
a =).° —(6
a)c112+E'cln(aE'c) +Lc
onde L é função do parâmetro a. Os outros coeficientes
podem calcular-se a partir de características do solvente
(D e 1), da temperatura e de constantes universais.
A verificação experimental mostrou que o parâmetro a
varia com D, o que carece de sentido.
A utilização do modelo hidrodinâmico manteve-se em
todas estas tentativas e nenhum outro tratamento frutífero é conhecido em que um modelo diferente tenha
sido empregado. O não conhecimento a priori do valor
do parâmetro a traz como consequência que ele tenha
de ser determinado ao mesmo tempo que se faz o cálculo de ).°.
A grandeza A. é a que tem real importância nos estudos
fundamentais da condutibilidade. Em soluções aquosas
não é possível trabalhar com concentrações muito baixas, dada a elevada condutibilidade específica do solvente, e por isso falham as equações em que o produto
xa foi desprezado em comparação com a unidade.
Nos dissolventes orgânicos, com pequenas condutibilidades específicas, é possível fazer estudos com soluções
mais diluídas, nas quais a aproximação é válida (desde
que a constante dieléctrica não seja muito baixa).
Verifica-se que a condutibilidade varia com a raiz quadrada da concentração, segundo uma lei linear, válida
Rev. Port. Qulm.,
8,
19, (1966)
CONDUTIBILIDADE IÓNICA
dentro do rigor experimental; simplesmente os coeficientes da recta não coincidem, em geral, com os previstos pela teoria (9). isto pode atribuir-se ao facto de
se formarem pares de iões que não são operantes do
ponto de vista da condutibilidade. ,'n dificuldade resolve-se, fàcilmente, introduzindo o grau de dissociação
e trabalhando com a expressão
ao — (9 a o + a) ✓ « c
Fuoss (10) e SHEDLOVSKY (11) forneceram métodos para
o cálculo de A., através desta equação.
Discutidas as possibilidades de estabelecimento dos termos AI e A1I e as limitações associadas, podemos voltar
ao termo mais importante A o (que traduz a condutibilidade liberta dos efeitos interiónicos) e procurar exprimi-lo em função de parâmetros característicos do sistema.
Com o arranjo dos termos, obtém-se:
IzIF2
,
ao =
X 1
6rNr
que traduz a regra de Walden, obtida por este autor,
como conclusão empírica, em 1906.
A verificação experimental da constância do produto
i. o que contém em si a essência da validade do modelo
hidrodinâmico foi ensaiada inúmeras vezes nos mais
distintos sistemas.
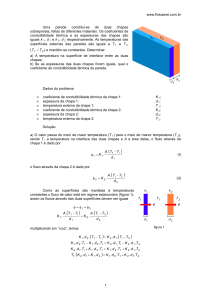
Com iões de dimensões elevadas e em soluções de dissolventes orgânicos, a constância do produto 71 A0 verifica -se só aproximadamente. Observa-se muitas vezes
o aparecimento de um máximo, quando se estuda a
variação deste produto com a temperatura, tal como
acontece no exemplo da fig. 1.
A.
1)
o
3 — MODELO HIDRODINÂMICO
C 5 H 5 NO,
0.590
O modelo mais simples a que pode recorrer-se é o modelo hidrodinâmico, que foi repetidamente empregado
no cálculo dos efeitos interiónicos.
Nele se assemelham os iões a esferas rígidas que se
movem em meio contínuo, viscoso e dieléctrico. Por
acção do campo eléctrico aplicado, as esferas são aceleradas até se atingir o equilíbrio com a resistência
oferecida ao movimento pelo meio viscoso.
Admite-se que no solvente não há movimentos próprios, nomeadamente que não existe movimento browniano.
Nestas condições, aplicando a lei de Stokes, obtém-se
fàcilmente, para a mobilidade de iões
ta= IzIeU
6r.r,r
usando a relação a o = Fµ vem:
,
z IF2
=
ór,rrN
onde a condutibilidade aparece explicitamente como
uma grandeza dependente da viscosidade do meio.
Rev. Port. Qutm.,
8. 19, (1966)
0,570
H2 0
^
CH 3 C0CH 3
0,550
0
20
40
60
80
100
t °C
Fig. I — Variação com a temperatura do produto de Walden, para o
picrato de tetraetilamónio, em acetona, água e nitrobenzeno.
Em solução aquosa, teremos para iões de grandes
dimensões, como os do exemplo escolhido, um comportamento semelhante, mas em iões de dimensões
muito menores a constância desaparece de forma quase
completa, notando-se uma tendência para aumentar o
produto 71 ao com a temperatura.
As experiências recentes feitas com solventes de alta
viscosidade (misturas de cianoetilsacarose e etanonitrilo)
revelam a forte dependência do produto de Walden da
viscosidade, a qual foi interpretada como sendo devida
ao facto de a resistência ao movimento iónico ser muito
inferior à prevista pelo modelo hidrodinâmico (12).
23
F. BARREIRA
A constância aproximada do produto de Walden, que
nalguns casos se verifica, não é altamente significativa,
porquanto os raios iónicos deduzidos da equação fundamental do modelo hidrodinâmico são muito diferentes dos raios cristalográficos.
A tentativa de sobrevivência do modelo fez com que
fossem propostas uma série de relações empíricas com
o fim de se obter melhor concordância entre a teoria
e a prática. Dentre eles citam-se a de ROBINSON e STOKES (13):
X°71
1
z F2
• 6
Nr
(f = f (r))
e as propostas por SUTRA (14), DARMOIS (15) e PRUE (16),
que usam diferentes funções do raio, partindo da hipótese da formação de complexos semipermanentes entre
os iões e o solvente. As características destes complexos
dependem das dimensões relativas dos iões e das moléculas do dissolvente.
Fuoss admitiu que a não verificação da constância do
produto de Walden se devia ao facto de as propriedades
microscópicas locais do solvente serem diferentes das
propriedades macroscópicas médias. Introduziu um
efeito de relaxação devido à orientação dos dipolos
do solvente, o qual seria dependente da constante dieléctrica. Este é o aperfeiçoamento mais fundamentado
que foi introduzido no modelo hidrodinâmico. A expressão final a que chegou, em substituição do produto
de Walden, é:
r = r
B D -1
onde r representa o raio do ião, num meio de constante dieléctrica infinita, onde os efeitos electrostáticos
estão ausentes.
Estas dificuldades reflectem perfeitamente a falta de
realismo do modelo que faz depender a condutibilidade
da viscosidade do meio.
O solvente não pode ser tomado como contínuo nem
o movimento como regular. Os iões são constituintes
menores de um arranjo molecular com movimentos
próprios a que se sobrepõe (às d.d.p. a que se trabalha) uma acção orientadora que provoca um deslocamento das cargas eléctricas.
A descrição realista de um tal sistema apresenta grandes
dificuldades. Propriedades muito mais simples, relacionadas com fenómenos de equilíbrio nas fases condensadas, não puderam ainda ser formuladas de maneira
.
24
satisfatória, em face do actual conhecimento das propriedades microscópicas locais dos líquidos, o que leva
a não abandonar totalmente o modelo hidrodinâmico
e a ele se terá de recorrer para interpretar uma série
de efeitos, como acontece, nomeadamente, com os
efeitos interiónicos.
4 — MODELOS CINÉTICO E ESTATISTICO
Nenhum dos modelos a que a seguir nos vamos referir,
embora baseados numa formulação mais correcta, atingiu o desenvolvimento suficiente para poder servir de
base ao estudo de relações quantitativas dos efeitos
interiónicos.
Se bem que certo progresso tenha sido realizado recentemente, no sentido da verificação experimental dos modelos mais perfeitos, registam-se, no entanto, dificuldades
que se cifram no facto de as equações derivadas conterem
quantidades que não podem ser determinadas independentemente, tornando a verificação directa impossível.
Até hoje, a única atitude praticável, no sentido de uma
verificação experimental, tem consistido em provocar
a variação de parâmetros externos ao sistema e observar
os efeitos desta variação sobre a condutibilidade equivalente a diluição infinita, deduzindo daí quantidades
derivadas cuja análise se pode fazer em termos de
propriedades intrínsecas do solvente.
Um dos modelos que envolvem uma descrição mais
correcta dos fenómenos de transporte em fase líquida
é o que se baseia na aplicação da teoria absoluta das
velocidades de reacção.
O movimento browniano é encarado como a resultante
de uma série de transições entre diferentes posições na
estrutura líquida, passando-se em cada uma dessas transições por estados activados. Admite-se que os líquidos
contêm lacunas de tamanho molecular e que uma molécula, ao deslocar-se para ocupar uma dessas lacunas,
adquire propriedades análogas às de uma molécula gasosa ( 1 ).
A acção do campo eléctrico consiste simplesmente numa
sobreposição orientadora ao movimento browniano, que
tem como resultado o movimento dos iões na direcção
do campo eléctrico.
As primeiras tentativas neste sentido foram feitas por
LINDEMANN (18) e MAGNUS (19), logo após o apareci( 1 ) Daqui as tentativas no sentido de relacionar, de forma simples,
a energia de activação com o calor de vaporização do solvente.
Rev. Port. Quím., 8, 19, (1966)
CONDUTIBILIDADE IÓNICA
mento da teoria cinética dos líquidos, mas as relações
quantitativas então obtidas não se ajustam às observações experimentais.
Devem-se a POLISSAR (20) e a EYRING (21) os tratamentos correctos, segundo este modelo, que permitiram
obter expressões válidas no sentido da tradução da
condutibilidade iónica em termos de grandeza mais
fundamentais. A equação básica é:
a„ =
I z eo FL2
6 h
A
Gó
e R
onde 0 G: representa a energia livre de activação do
processo translacional e é medida pela diferença de
energias livres entre o estado inicial e o estado de
transição. O parâmetro L representa a deslocação sofrida pelo ião entre duas posições sucessivas.
A validade desta equação depende de dois factores:
i) A correcção do factor de frequência aplicado ao
fl uido denso
ii) A aplicação da termodinâmica de equilíbrio à energia de activação.
Deve assinalar-se uma extensão dos resultados deste
modelo a soluções de concentração não nula devida
a PODOLSKY (22), que tratou em conjunto os problemas
da viscosidade, difusão e condutibilidade iónica, admitindo que a energia livre de activação é a mesma para
os três processos. Ao considerar o efeito da presença
dos iões na solução, recorreu à equação semiempírica
de Jones e Dole:
= ^1 (1 + A ✓
B c),
retendo selmente o termo em c, que corresponde às
interacções ião-molécula, e desprezando o termo em c 1 / 2 ,
que diz respeito às acções interiónicas.
No desenvolvimento do cálculo desaparece a concentração, dado que só foi considerado o termo em c, e
assim não é possível recorrer a este tratamento do
problema para traduzir a variação da condutibilidade
com a concentração. De resto, a utilização da equação
semiempírica de Jones e Dole não está suficientemente
fundamentada. A hipótese da igualdade das energias
de activação para os três processos translacionais cria
uma interdependência entre a condutibilidade e a visRev. Port. Qufm., 8, 19, (1966)
cosidade, de que já enfermava formalmente o modelo
hidrodinâmico.
Recentemente, a escola de KIRKWOOD (23) publicou
uma série de trabalhos que têm como objectivo fornecer um tratamento estatístico do movimento molecular e da migração iónica. Consideram que a energia
eléctrica é dissipada em colisões entre elementos rígidos
e em interacções elásticas. As primeiras são características das massas em colisão e as segundas das interacções entre as esferas em movimento e os seus vizinhos.
A relação final obtida tem a forma
eo F
ao
8
(-2nmmlkT1
— N a g (a)
m + m1
3
-
, ,.
I
diâmetro da colisão de um ião e uma molécula
m — massa do ião
m 1 — massa da molécula
g(a) — função de correlação
No denominador o primeiro termo diz respeito às colisões entre elementos rígidos e o ; representa um coeficiente de fricção que intervém em correspondência com
as interacções elásticas e que pode ser calculado pelas
expressões:
/ 4 nm1c 3 p mt
21
_
S o
s p m1
^
72 V (R) g(R) dR
onde pm 1 é a densidade mássica do fluido, c a velocidade do som no fluido. V(R) é o potencial do par
intermolecular e g (R) a equação de correlação.
A noção básica deste modelo consiste no facto de os
iões praticarem choques rígidos com as moléculas e
depois destes choques seguirem uma trajectória determinada por um campo de forças rapidamente flutuante
em que intervêm todas as moléculas vizinhas. O campo
relaxa num intervalo de tempo pequeno comparado com
o intervalo entre duas colisões e a trajectória dos iões
é tomada como quase aleatória.
Em resumo, é possível dispor de três tipos de modelos
para a descrição da condutibilidade equivalente.
O modelo hidrodinâmico, cuja estruturação se pode
considerar defeituosa em face dos actuais conhecimentos
das propriedades do estado líquido, mas que não pode
ser fàcilmente abandonado, por ser de todos o mais
25
F. BARREIRA
manejável e se prestar para o tratamento do efeito interiónico. No outro extremo figura o modelo estatístico,
onde se fazem intervir particularidades microscópicas
do sistema, mas no qual a análise quantitativa fica dependente de vários parâmetros que se não conhecem
senão, quando muito, de forma aproximada e cujo cálculo, para a maior parte dos sistemas, não é possível.
Em situação intermediária aparece o modelo cinético,
fundamentado nos princípios da teoria cinética dos líquidos e na teoria das velocidades absolutas de reacção,
que tão frutuosos resultados têm dado no tratamento
de muitos outros problemas.
Presta-se este modelo, em particular, para a determinação de parâmetros fundamentais característicos dos
líquidcs, quando se estudam as variações sofridas pela
condutibilidade, em função da alteração de parâmetros
exteriores ao sistema, nomeadamente a pressão e a
temperatura.
Assim, as energias de activação a pressão constante
e volume constante, que são definidas pelas relações:
d
^
Ep=RT' lni.°
dT
O In
-- °
dT
^
^p
podem, em face da equação fundamental do modelo
cinético, ser interpretadas em termos de parâmetros
mais fundamentais.
Para isso há que fazer hipóteses quanto aos valores do
parâmetro L, que nos é desconhecido. BRUMMER e
HtLLS (24), para resolver esta dificuldade, admitiram
que L era proporcional à potência 1 /3 do volume especifico do líquido; com esta hipótese as derivadas podem
ser calculadas e tem-se:
E„= A Uõ
Paralelamente, a variação da condutibilidade equivalente com a pressão permite calcular o volume de
activação, que é dado por
d^
A V*=
Gó
d P
T
Da equação fundamental tira -se fàcilmente:
JV*=— RTLI d
dP
°
)T
+
d
3
Todas estas quantidades podem ser calculadas a partir
de dados obtidos com soluções de concentração não
nula, quer dizer, sem se terem eliminado os efeitos
interiónicos.
Para estudar a variação destas grandezas com a concentração, teremos de recorrer, de novo, ao modelo
hidrodinâmico, através da equação de Onsager.
Aplicando-a, obtém-se, por exemplo, para a energia de
activação a pressão constante:
(E )
I (E
)
RT2 RT'- ï.° 1 L RT=^
1I
(dk)
dT p
(com k = 8 k° +
k
^
vc
c
a)
k
para soluções diluídas pode desprezar-se — c em presença de ✓c e obtém-se assim uma variação linear
de E com v'c .
De forma análoga se estabelecia a variação com a
concentração das duas outras grandezas derivadas.
Ep=OHó+—RT2«
3
E p — E„ (Is + P) 0 V *+ 3 RT2 a
Este resultado põe em evidência a diferença entre as
energias de activação a pressão constante e volume
constante e que a segunda é uma quantidade muito
mais simples que a primeira. As reacções a volume
constante na fase líquida são as mais importantes, visto
a energia da fase condensada ser função das distâncias
intermoleculares.
26
BIBLIOGRAFIA
Arrhenius, S. A., Z. Physik. Chem., I, 631 (1887).
Norberg, K., Acta Chim. Scand. 20, 164 (1966).
Onsager, L., Z. Physik. 28, 277 (1927).
Onsager, L. e Fuoss, R. M., J. Phys. Chem.. 36, 2689 (1932).
5. Shedlovsky, T., J. Am. Chem. Soc., 54, 1405 (1932).
1.
2.
3.
4.
Rev. Port. Quim.. 8. 19, (1966)
CONDUTIBILIDADE TÓNICA
6.
Falkenhagen, H. e Kelbg, G., Z. Elektrochent., 58, 653
(1954).
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
Fuoss, R. M. e Onsager, Z., J. Phys. Chem., 61, 668 (1957).
Fuoss, R. M. e Onsager, Z., J. Phys. Chem., 62, 1339 (1958).
Fuoss, R. M., Onsager, Z. e Skinner, J. F., J. Phys. Chem.,
69, 2581 (1965).
Barreira, F., Rev. Port. Quail., 5, 133 (1963).
Barreira, F., Rev. Port. Quint., 5, 194 (1963).
Fuoss, R. M., J. Am. Chem. Soc., 57, 488 (1935).
Shedlovsky, T., J. Franklin Inst., 225. 739 (1938).
Treiner, C. e Fuoss, R. M., J. Phys. Cheat., 69, 2576 (1965).
Robinson, R. A. e Stokes, R. H., «Electrolyte Solutions»,
Butterworths, London 1959, p. 124.
Sutra, G., J. Chico. Phys., 43, 279 (1946).
Darmois, E., J. Chita. Phys., 43, 1 (1946).
Prue, J. F. e Sherrington, P. J., Trans. Faraday Soc., 57,
22. Podolsky, R. J., J. Am. Chem. Soc., 80, 4442 (1958).
23. Alnatt, A. R. e Rice, S. A., J. Cheat. Phys., 34, 2156 (1961).
Rice, S. A. e Alnatt, A. R., J. Chem. Phys., 34, 2144 (1961).
Davis, A. T.. Rice, S. A. e Meyer, L., J. Chem. Phys., 37,
1521 (1962).
24.
Brumer, S. B. e Hills, G. J., Trans. Faraday Soc., 57, 1816
(1961).
SUMMARY
1795 (1961).
1.7.
18.
19.
20.
21.
Fuoss, R. M., Proc. Nat. Arad. Sei. U. S., 45, 807 (1959).
Lindemann, F. A., Z. Physik. Chem., 110, 394 (1924).
Magnus, A., Z. Physik. Chem., 174A, 262 (1935).
Polissar, M. J., J. Chem. Phys., 6, 833 (1938).
Glasston, S., Laidler, K. J. e Eyring, H., «The Theory of
Rate Processes», Mc Graw-Hill, New York 1941, p. 552.
Rev. Port. Qutnt.,
8, 19, (1966)
The ionic conductivity is considered in terms of the three principal models — the hydrodynamic, the kinetic and the statistic.
Their fundaments are discussed and also their usefulness on
the study of the concentration effect upon conductivity. The
accuracy and the experimental test of the three models are
examined.
27
i