Importante:

Lista1: Cinemática Unidimensional
Lista 1: Cinemática Unidimensional
NOME:______________________________________________________________________
Matrícula:
Turma:
Prof. :
Importante:
i. Nas cinco páginas seguintes contém problemas para serem resolvidos e entregues.
ii. Ler os enunciados com atenção.
iii. Responder a questão de forma organizada, mostrando o seu raciocínio de forma coerente.
iv. Analisar a resposta respondendo: ela faz sentido? Isso lhe ajudará a encontrar erros!
1. Dois carros, A e B, se movem ao longo da linha horizontal, eixo X. O carro A parte da posição 2,00m
com velocidade 0,60m/s e com aceleração constante 2,00m/s2. O carro B se move a velocidade
constante de 4,50m/s partindo da origem. (a) Escreva as equações de posição para cada veículo. (b)
Para que tempos(s), caso exista algum, A e B possuem a mesma posição? (c) Para que tempos(s),
caso exista algum, A e B possuem a mesma velocidade? (d) Verifique as respostas dos itens (b) e (c)
construindo os gráficos de posição x versus o tempo t e de velocidade v versus t, no intervalo de t=0 a
t=4,00s.
1
Lista1: Cinemática Unidimensional
2. Uma lebre e uma tartaruga principiam uma corrida de 10km no instante t=0 s. A lebre corre a 4,0m/s e
rapidamente se distancia da tartaruga, que vai a 1 m/s. Depois de 5,0 min, a lebre para e resolve dormir
um pouco. A soneca dura 135 min.. Passados estes, a lebre acorda e retoma a corrida a 4m/s, mas perde
para a tartaruga. (a) Faça o gráfico de x versus t, nos mesmos eixos, para a lebre e tartaruga. (b) Em
que instante esta ultrapassa aquela? (c) Qual a distância entre as duas, quando a tartaruga cruza a linha
de chegada? (d) Quanto tempo poderia a lebre dormir e ainda vencer a prova?
2
Lista1: Cinemática Unidimensional
3.
A posição de uma partícula movendo-se ao longo do eixo X depende do tempo de acordo com a
expressão, x(t) = 3,0t2 -1,0 t3, onde x é dado em metros e t em segundos. (a) Quais as unidades dos
coeficientes 3,0 e de 1,0 da equação x(t) ? (b) Para que instante t a partícula atinge a posição máxima?
(c) Qual é a velocidade média durante os primeiros 2,5s? É possível conhecer o sentido do movimento?
Explique. (d) Qual é a velocidade instantânea v(t) em 2,5s? É possível conhecer o sentido do
movimento? Explique. (e) Trace o gráfico de x versus t para t =0 a t=4,0 s e indique como as respostas de
(c) e (d) podem ser encontradas no gráfico.
3
Lista1: Cinemática Unidimensional
é lançado verticalmente e sobe com uma aceleração constante de 20,0m/s2 durante um
minuto. O seu combustível acaba e ele continua a mover-se como uma partícula em queda livre. (a) Qual é
a altura máxima atingida pelo foguete? (b) Qual o tempo total percorrido entre o lançamento até o retorno
ao solo? (c) Faça o gráfico de posição versus tempo desde o lançamento até o retorno ao solo.
4. Um foguete
4
Lista1: Cinemática Unidimensional
5. Uma garota avista um pote de flores passar subindo e a seguir descendo por uma janela com 1,1 m de
altura. O tempo total durante o qual o pote é visto é de 0,74s. Determine a altura alcançada pelo pote acima
do topo da janela. .
5
Lista1: Cinemática Unidimensional
Questões:
(A) É possível que a velocidade média, num dado intervalo de tempo, seja zero, apesar de a velocidade
média num intervalo de tempo menor, incluído no primeiro, não ser nula? Explique usando um gráfico
x em função de t.
(B) É possível existir uma aceleração nula e velocidade diferente de zero? Explique usando um gráfico v
em função de t.
(C) Você lança uma bola de tênis verticalmente para cima e ela atinge uma altura máxima maior do que a
sua altura. O módulo da aceleração é enquanto ela está sendo lançada ou logo depois que ela deixa a
sua mão? Explique.
(D) Um objeto é lançado para cima de uma altura h. Mostre que o tempo para que ele retorne à sua posição
inicial de lançamento é igual ao dobro do tempo que o objeto leva para atingir sua posição máxima.
(E) Um objeto é lançado com velocidade vo para cima de uma altura h. Mostre que a velocidade com que
ele passa, no retorno, pela posição de lançamento é a mesma em módulo.
Exercícios e Problemas
1. Sejam os vetores A, B e C indicados na figura com as suas magnitudes e direções. (a)
cada vetor indicado na figura em termos dos vetores unitários i
e j. (b) Utilizando o método das componentes, determine o
módulo, a direção e o sentido da soma vetorial A + B. Calcule,
novamente, o módulo dessa soma utilizando a lei dos cossenos.
(c) Calcule o vetor D tal que satisfaça a equação A +B + C
+D =0. Esboce-o na figura. (d) Determine o ângulo que o vetor
D faz com o eixo x positivo.
2. Uma partícula parte da origem em t=0 e se move ao longo eixo x.
O gráfico da velocidade da partícula em função do tempo é mostrado
na figura. (a) Em que intervalo de tempo a aceleração é positiva,
negativa ou nula? (b) Qual é a distância percorrida pela partícula em
16s?
3. Em t=0, um alpinista, de forma acidental, deixa um grampo
cair livremente em um ponto alto de um paredão de rocha
até um vale abaixo. Após um curto intervalo de tempo, seu
6
Escreva
Lista1: Cinemática Unidimensional
companheiro de escalada, que está 10 m acima dele no paredão, lança outro grampo para baixo. As
posições y dos grampos versus t durante as quedas são dadas na figura. Com que velocidade o segundo
grampo foi lançado? Resp.: 17 m/s.
4. Uma bola é lançada verticalmente, eixo-Y, para baixo de uma altura de 50,0m com velocidade inicial
de 20,0m/s. (a) Expresse o vetor posição y da bola. (b) Qual é a sua velocidade exatamente antes de
atingir o solo? (c) Quanto ela leva para chegar ao solo? (d) Se a bola fosse jogada verticalmente para
cima, da mesma altura e com a mesma velocidade inicial, quais seriam as respostas aos itens (a), (b) e
(c) ? (e) Nos dois casos, qual é a interpretação para o tempo negativo? Sugestões: Considere a origem
das coordenadas no solo e g=10,0m/s2 para facilitar as contas.
Resp.:(a) y = y(t)j = (50,0-20,0 t-5,00 t2)j (m);(b) v = - 37,4j (m/s);(c) t=1,74s;(d) y(t) = (50,0 + 20,0t 5,00 t2)j, v = -37,4(m/s); t=5,74 s.
5. O elevador de um edifício percorre no total 187 m e sua velocidade escalar máxima é de 5,00m/s e a
aceleração constante é de 1,20m/s2 . (a) Que distância percorre o elevador ao acelerar a partir do
repouso até alcançar sua velocidade escalar máxima? (b) Qual é o tempo gasto pelo elevador para
percorrer os 187m, partindo do repouso e terminando em repouso?
6. A figura mostra a velocidade v versus a altura y para uma
bola lançada diretamente para cima, ao longo do eixo y. A
velocidade na altura yA é vA. A velocidade na altura yB é
vA/3. A distância d é 0,40m. Quanto vale a velocidade vA?
7. Uma pedra é atirada verticalmente para cima a partir da borda do topo de um edifício. A pedra atinge
sua altura máxima acima do topo do edifício 1,60s após ter sido atirada. Então, após quase tocar a
borda do edifício em seu movimento para baixo, a pedra atinge o chão 6,00s após ter sido lançada. (a)
Com que velocidade a pedra foi lançada para cima? (b) Qual é a altura máxima acima do topo do
edifício alcançada pela pedra e, (c) qual é a altura do edifício? Resp.: (a) 15,7m/s; (b) 12,5m; (c) 82,3m.
8.
Quando um balão científico descontrolado sobe a 19,6m/s, um de seus
conjuntos de instrumentos desprende-se e cai livremente. A figura
fornece a velocidade vertical do conjunto versus tempo, do momento
em que se desprende até o instante em que atinge o solo. (a) Qual a
altura máxima que ele atinge a partir do ponto em que se desprende? (b)
Em que ponto acima do solo o conjunto se desprende? Resp.: (a) 20m;
(b) 59m.
7
Lista1: Cinemática Unidimensional
9. Uma bola é lançada verticalmente para baixo com uma velocidade inicial v0 de uma altura h. (a) Qual
é sua velocidade imediatamente antes de atingir o solo? Quanto tempo a bola leva atingir o solo? Quais
seriam as respostas (c) do item (a) e (d) do item (b) se a bola fosse lançada para cima da mesma altura
e com a mesma velocidade inicial? Nota.: Antes de resolver qualquer equação, decida se as respostas
de (c) e (d) deveriam ser maiores, menores, ou iguais àquelas de (a) e (b). Resp.: (a) v = (v0 + 2g h)0,5;
(b) t = [(v0 + 2g h)0,5-v0]/g; (c) mesma de (a); (d)
t = [(v0 + 2g h)0,5+v0]/g, maior.
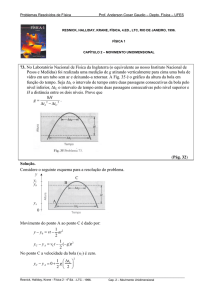
10. No laboratório foi realizada uma medida da aceleração de queda livre g lançando-se uma bola de vidro
para cima em um tubo evacuado e deixando-a retornar. Seja ∆TL na figura o intervalo de tempo entre
duas passagens da bola através de certo nível inferior, ∆TU o intervalo de certo tempo entre as duas
passagens por um nível superior e H a distância entre os dois níveis. Mostre que g = 8 H/(∆T2L-∆T2U) .
8