PDF - ELITE CAMPINAS

OS MELHORES GABARITOS DA INTERNET: www.elitecampinas.com.br
O ELITE RESOLVE IME 2011 – FÍSICA DISCURSIVAS
(19) 3251-1012
FÍSICA
Isolando a incógnita Q , obtemos:
⎛L
⎞ P ⋅c
Q = ⎜ − 1⎟ ⋅
L
⎝ 0
⎠ g ⋅α
QUESTÃO 01
Do enunciado,
P ⋅ c 50 + 30 2
=
J , logo:
g ⋅α
3 2
⎛5−3 2 ⎞
⎛5+3 2⎞
⎛ 5
⎞ ⎛ 50 + 30 2 ⎞
Q=⎜
− 1⎟ ⋅ ⎜
⎟⎟ ⇒ Q = ⎜⎜
⎟⎟ ⋅ 10 ⋅ ⎜⎜
⎟⎟ ⇒
⎜
3
2
3
2
3
2
⎝
⎠ ⎝
⎠
⎝
⎠
⎝ 3 2 ⎠
35
⎛ 25 − 18 ⎞
Q=⎜
J
⎟ ⋅ 10 ⇒ Q =
18
9
⎝
⎠
A figura acima mostra um sistema composto por uma parede vertical
com altura H, uma barra com comprimento inicial L0 e uma mola. A
QUESTÃO 02
barra está apoiada em uma superfície horizontal sem atrito e presa no
ponto A por um vínculo, de forma que esta possa girar no plano da
figura. A mola, inicialmente sem deformação, está conectada à parede
vertical e à barra.
Após ser aquecida, a barra atinge um novo estado de equilíbrio
térmico e mecânico. Nessa situação a força de reação vertical no
apoio B tem módulo igual a 30 N. Determine a quantidade de calor
recebida pela barra.
Dados:
• H = 3m
• L0 = 3 2 m ;
• o peso da barra: P = 30 N;
• constante elástica da mola: k = 20 N/m;
•
Pc 50 + 30 2
joules, onde c é o calor específico da barra; α é o
=
gα
4
coeficiente de dilatação linear da barra; g é a aceleração da gravidade;
e P é o peso da barra.
Resolução
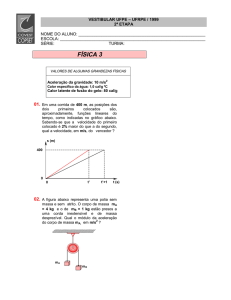
Um corpo está sobre um plano horizontal e ligado a uma mola. Ele
começa a ser observado quando a mola tem máxima compressão
(Figura 1a). Durante a observação, verificou-se que, para a
deformação nula da mola (em x = 0), sua velocidade é 5 m/s (Figura
1b). Para x = 0,2 m (Figura 1c), o corpo é liberado da mola a partir
dessa posição e fica submetido a uma força de atrito até parar. Faça
um gráfico da aceleração a do corpo em função da posição x,
registrando os valores de a e de x quando:
JG
R Ay
A
JG
R Ax
L0
JG L
P
30N
kx
E
D
C
a) a observação se inicia;
b) a velocidade é máxima;
c) o corpo é liberado da mola;
d) o corpo para.
Equilíbrio de forças sobre a barra:
Vertical: −P + 30 + RAy = 0 ⇒ RAy = 0 N
Horizontal: −kx + RAx = 0 ⇒ RAx = kx
Dados:
• massa do corpo: 500 g;
• constante elástica da mola: 50 N/m;
• coeficiente de atrito entre o plano e o corpo: 0,3.
O comprimento da mola sem deformação é facilmente obtido a partir
de H e L0 e é igual a CD = 3 m, assim, na situação de equilíbrio final,
CE = 3 + x , onde x é a deformação da mola.
Resolução
Temos duas hipóteses para resolver o problema, uma vez que não fica
claro se o atrito entre o corpo e o plano age enquanto este fica preso à
mola ou se ele passa a agir apenas após o corpo se soltar da mesma.
Primeira hipótese (atrito age apenas após o corpo se soltar):
•
Para −b ≤ x < +0,2 m não há atrito entre o corpo e o plano.
Equilíbrio de Momentos em relação ao pólo A:
(3 + x )
−kx ⋅ 3 + 30 ( 3 + x ) − 30
= 0 ⇒ −20 x + 5 ( 3 + x ) = 0 ⇒
2
−15 x = −15 ⇒ x = 1m
Considerando
a
situação
de
equilíbrio
final,
temos
que
•
CE = ( 3 + 1) m ⇒ CE = 4 m . Logo, o comprimento final da barra é
2
Para a dilatação linear podemos escrever:
L = L0 (1 + αΔθ ) , onde Δθ é a variação de temperatura.
(1)
G
Fmola ( −kx )
Ainda, sobre o calor recebido pela barra, podemos escrever:
P
Q = m ⋅ c ⋅ Δθ , como m = , temos:
g
(2)
Δθ =
Para +0,2 m ≤ x < xfinal há atrito entre o corpo e o plano.
Diagrama de corpo livre para −b ≤ x < +0,2 m :
G
Forças agindo sobre o corpo nesse
N
trecho:
dado por: L2 = (CE ) + ( AC ) = 42 + 32 (m 2 ) ⇒ L = 5 m .
2
G
P
g ⋅Q
P ⋅c
Fresultante = Fmola = −50 x
Aceleração do corpo nesse trecho:
F
50 x
a = resultante = −
= −100 x
m
0,5
Escrevendo as equações de conservação de energia comparando o
instante em que x = −b com o instante em que x = 0 (instante no
qual a velocidade do corpo é máxima):
k ⋅ b 2 m ⋅ v máx 2
m
=
⇔ b 2 = v max 2 ⋅
k
2
2
Substituindo (2) em (1):
⎛ Q⋅g ⋅α⎞
L = L0 ⎜ 1 +
P ⋅ c ⎟⎠
⎝
1
OS MELHORES GABARITOS DA INTERNET: www.elitecampinas.com.br
O ELITE RESOLVE IME 2011 – FÍSICA DISCURSIVAS
(19) 3251-1012
Escrevendo o Teorema da Energia Cinética comparando o instante em
que x = −b com o instante em que x = 0 (instante no qual a
velocidade do corpo é máxima):
Como b > 0 por hipótese:
0,5
= 0,5 m
50
Diagrama de corpo livre para +0,2 m ≤ x < xfinal :
b = 5⋅
JJG
Fat = μc ⋅ N = 0,3 ⋅ 5 = 1,5 N (para a
esquerda)
Por praticidade, podemos assumir que 10036 100 .
Como b > 0 por hipótese:
b = +0,53m
Aceleração do corpo nesse trecho:
F
1,5
G
a = resultante =
= 3 m s 2 (para a
P (5 N )
m
0,5
esquerda)
Encontremos então a velocidade do corpo no instante em que ele se
solta da mola, conservando energia entre o instante de compressão
máxima e o instante em que x = +0,2 m :
G
Fat
Diagrama de corpo livre para +0,2 m ≤ x < xfinal :
G
Assim como na 1ª hipótese temos apenas a
N
força de atrito agindo nesse trecho.
Aceleração do corpo nesse trecho:
F
1,5
a = resultante =
= 3 m s 2 (para a
m
0,5
esquerda)
Encontremos então a posição na qual o corpo para, aplicando o
Teorema da Energia Cinética entre o instante de deformação nula da
mola e o instante em o corpo para ( x = xfinal ):
G
Fat
k ⋅ b 2 k ⋅ 0,22 m ⋅ v saída 2
=
+
2
2
2
2
2
2
0,5 ⋅ v saída
50 ⋅ 0,5
50 ⋅ 0,2
=
+
∴ v saída = 21 m s
2
2
2
Agora vamos calcular quanto o corpo anda desde o instante em que
ele se desprende da mola até parar usando Torricelli.
02 = v saída 2 − 2 ⋅ a ⋅ d
Assim temos que xfinal
G
P
m ⋅ v max 2
k ⋅ 0,22
− Fat ⋅ xfinal −
=0⇔
2
2
0,5 ⋅ 52
50 ⋅ 0,22
− 1,5 ⋅ xfinal −
= 0 ⇔ xfinal = 3,5 m
2
2
Vamos então, finalmente, calcular a aceleração do corpo nos pontos
pedidos no enunciado:
a) Estamos supondo que existem forças de atrito estático no instante
inicial (instante em que o corpo ainda não adquiriu velocidade). Como
há uma força elástica solicitando o início do movimento, estamos
considerando que o coeficiente de atrito estático é igual ao coeficiente
de atrito cinético (situação bastante comum), desta forma temos que
a = −100 ⋅ x − 3 = −100 ⋅ ( −0,53 ) − 3 ⇒ a = 50 m s 2 .
2
v saída
21
=
= 3,5 m
2⋅a
2⋅3
= 0,2 + 3,5 = 3,7 m .
d=
JJG
m ⋅ v máx 2
k ⋅ b2
− 1,5b =
2
2
Substituindo os valores, obtemos a seguinte equação do 2º grau em b:
100b 2 − 6b − 25 = 0 ⇒ Δ = 10036
Forças agindo sobre o corpo nesse trecho:
P = N = 0,5 ⋅ 10 = 5 N
G
N (5 N )
JJG
τ( F resultante ) = τ( F MOLA ) + τ( F at ) = ΔECIN
Vamos então finalmente calcular a aceleração do corpo nos pontos
pedidos no enunciado:
a) x = −0,5 m ⇒ a = −100 ⋅ ( −0,5 ) ⇒ a = +50 m / s 2 .
b) A velocidade é máxima no instante em que a extremidade da mola
passa pelo ponto de deformação nula: x = 0 m ⇒ a = 0 m / s 2 .
c) Logo após ser liberado da mola, apenas a força de atrito age, e daí
temos que a = −3 m s 2 (referencial positivo para a direita).
b) A velocidade é máxima no instante em que a força resultante se
anula, ou seja, no instante em que a aceleração se anula. Nesse caso,
temos:
a = 0 ⇔ −100 x − 3 = 0 ⇔ x = −0,03 m
c) Logo após ser liberado da mola, apenas a força de atrito age, e daí
temos que a = −3 m s 2 (referencial positivo para a direita).
d) Quando o corpo para (ou seja, quando x = xfinal ), a força de atrito
cinético deixa de agir, e por isso a resultante é nula e temos a = 0 .
Então podemos esboçar o gráfico pedido:
(Aceleração X Posição)
a (m / s2 )
50
d) Quando o corpo para (ou seja, quando x = xfinal ), a força de atrito
cinético deixa de agir, e por isso a resultante é nula e temos a = 0 .
Então podemos esboçar o gráfico pedido:
(Aceleração X Posição)
a (m / s2 )
0,2
-0,5
0
-3
3,7
50
x (m)
-20
Segunda hipótese (atrito age desde o início):
Diagrama de corpo livre para −b < x < +0,2 m :
Forças agindo sobre o corpo nesse
G
trecho:
N
Fmola = −50 x
G
Fat = μc N = 0,3.5 = 1,5N
Fmola ( −kx )
G
Fresultante = Fmola − Fat = −50 x − 1,5
Fat
G
P
Aceleração do corpo nesse trecho:
F
−50 x − 1,5
= −100 x − 3
a = resultante =
m
0,5
0,2
-0,53
-0,03
-3
-23
2
3,5
x (m)
OS MELHORES GABARITOS DA INTERNET: www.elitecampinas.com.br
O ELITE RESOLVE IME 2011 – FÍSICA DISCURSIVAS
(19) 3251-1012
QUESTÃO 03
b) A aceleração centrípeta será: acp =
v²
,na direção y.
L
JG
T
Da figura, considerando que –Q
está em movimento circular,
temos:
⎧⎪RCP = T − P − FEy
⎨
⎪⎩RT = FEx
JG
F Ex
JG
F Ey
JG
FE
Portanto, a componente tangencial da resultante será dada pela
componente x força eletrostática:
k⋅Q ⋅Q
RT = FEx ⇒ m ⋅ aT =
⋅ cos β ⇒
r²
Uma carga positiva está presa a um espelho plano. O espelho
aproxima-se, sem rotação, com velocidade constante paralela ao eixo
x, de uma carga negativa, pendurada no teto por um fio inextensível.
No instante ilustrado na figura, a carga negativa se move no sentido
oposto ao da carga positiva, com a mesma velocidade escalar do
espelho. Determine, para esse instante:
a) as componentes x e y do vetor velocidade da imagem da carga
negativa refletida no espelho;
b) as acelerações tangencial e centrípeta da carga negativa;
c) as componentes x e y do vetor aceleração da imagem da carga
negativa refletida no espelho.
aT =
(
2
kQ ²
m⋅ d
sen β
)
2
⋅ cos β ⇒ aT =
k ⎛ Q ⋅ sen β ⎞
⎟ ⋅ cos β , no sentido
m ⎜⎝
d
⎠
negativo de x.
G
G
c) Como o espelho está em movimento uniforme ( aespelho = 0 ), a
aceleração da imagem no referencial do espelho e em um referencial
em repouso são iguais, logo, podemos utilizar a figura a seguir para
calcular ax e ay.
Dados:
• ângulo entre o eixo x e o espelho: α;
• ângulo entre o eixo x e o segmento de reta formado pelas cargas: β;
• diferença entre as coordenadas y das cargas: d;
• comprimento do fio: L;
• velocidade escalar do espelho: v;
• módulo das cargas elétricas: Q;
• massa da carga negativa: m;
• constante elétrica do meio: K.
Resolução
Admitindo-se que, no instante dado, a velocidade de -Q esteja na
direção horizontal, temos:
a) Em relação ao espelho, a velocidade relativa de -Q será 2v. Pela
figura a seguir, obtemos as componentes x e y da velocidade da
imagem relativa ao espelho:
y
180º - 2 α
2 α - 90º
acp
90º - α
α
at
2 α - 90º
180º - 2 α
90º - α
α
α
α
at
acp
Carga -Q
⎧⎪ay = acp sen(2α − 90º ) − at cos(2α − 90º )
⇔
⎨
⎪⎩ax = acp cos(2α − 90º ) + at sen(2α − 90º )
⎧
v2
kQ 2
sen(2α ) −
sen2 β.cos β ⋅ cos(2α )
⎪ ax =
L
md 2
⎪
⇔⎨
⎪
v2
kQ 2
sen2 β ⋅ cos β ⋅ sen(2α )
⎪ ay = − cos(2α ) −
2
L
md
⎪⎩
x
90o − α
90o − α
2α − 90o
JJG
v'
JG
P
90o
QUESTÃO 04
90o − α
JJG
Da figura, temos: v ' =2v, logo, as velocidades relativas ao espelho
são:
⎪⎧v ' x = 2v sen ( 2α − 90° ) = −2v sen ( 90° − 2α ) = −2v cos ( 2α )
⎨
⎪⎩v 'y = −2v cos ( 2α − 90° ) = −2v cos ( 90° − 2α ) = −2v sen ( 2α )
Para em referencial fixo, o espelho possui velocidade v no eixo x, logo,
para um observador no solo:
v x = −2 v cos ( 2α ) + v ⇒ v x = v ⋅ (1 − 2cos ( 2α ) )
v y = v 'y = −2 v sen ( 2α )
De acordo com a figura acima, um raio luminoso que estava se
propagando no ar penetra no dielétrico de um capacitor, é refletido no
centro de uma das placas, segundo um ângulo α, e deixa o dielétrico.
A área das placas é A e o tempo que o raio luminoso passa no interior
do dielétrico é t. Supondo que se trata de um capacitor ideal de placas
3
OS MELHORES GABARITOS DA INTERNET: www.elitecampinas.com.br
O ELITE RESOLVE IME 2011 – FÍSICA DISCURSIVAS
(19) 3251-1012
A figura acima apresenta um prisma apoiado em um elevador no
interior de um cilindro de material isolante. Uma armação, encostada
no prisma, é composta por uma parte metálica com resistência
desprezível em forma de “U” e por uma barra metálica de 0,25 m e
resistência de 1 Ω. Essa barra desliza ao longo da barra em “U”,
mantendo o contato elétrico. As extremidades da armação em “U” são
fixadas no cilindro, conforme a figura. Ao longo de todo o cilindro, um
fio é enrolado, formando uma bobina com 1000 espiras, perfazendo
uma altura h = 0,8 m, sendo alimentada por uma fonte, de modo que
103
A. O elevador sobe com velocidade
flua uma corrente de
π
constante v, de modo que seja exercida sobre a barra metálica
2
uma força normal de
N. Determine a velocidade v.
4
paralelas e que o dielétrico é um bloco de vidro que preenche
totalmente o espaço entre as placas, determine a capacitância do
capacitor em picofarads.
Dados:
• A = 1,0 cm2
• t = 2,0 × 10–12 s
• α = 30°
• permissividade elétrica do vácuo: εo ≈ 9,0 × 10–12 F/m
• velocidade da luz no vácuo: c ≈ 3,0 × 108 m/s
• índice de refração do vidro: n = 1,5
• constante dielétrica do vidro: k = 5,0
Resolução
Como a luz foi refletida na parede interna do capacitor, o ângulo de
entrada é igual ao de saída. Além disso, temos algumas relações
geométricas como mostrado na figura abaixo:
Dados:
• as faces triangulares do prisma são triângulos retângulos isósceles;
• permeabilidade magnética do meio: μ0 = 4π.10-7 Tm/A
d
α
Observações:
• não há atrito em nenhuma parte do sistema;
• a barra metálica é feita de material não magnético;
• as espiras percorrem todo o cilindro.
Resolução
d
JJG
As forças que atuam na barra são uma força vertical Fy (que seria a
soma vetorial do peso da barra com alguma força de contato normal à
JJG
armação em “U”), a força de origem magnética Fm e a força de
JJG
contato N , normal à barra. Elas estão indicadas na figura a seguir:
JJG
d ⋅ sen α
Dado que a luz mudou de meio, sua velocidade se alterou para v vidro :
v vidro =
c
nvidro
=
3 ⋅ 108
= 2 ⋅ 108 m/s
1,5
N
Dentro do vidro, a luz percorreu uma distância igual a 2 ⋅ d num tempo
t = 2 ⋅ 10−12 s :
v vidro =
v
⋅ t 2 ⋅ 108 ⋅ 2 ⋅ 10 −12
2⋅d
⇒ d = vidro =
= 2 ⋅ 10−4 m
t
2
2
JJJG
suas placas é
capacitância:
1 cm = 10
2
C=
C=
5 ⋅ ( 9 ⋅ 10
−4
−12
−4
45°
JJG
Fm
Como a distância entre as placas do capacitor é d ⋅ sen α e a área de
N
JJG
Fy
2
m , podemos então calcular sua
45°
εvidro ⋅ A kvidro ⋅ ε0 ⋅ A
=
⇔
d ⋅ sen α
d ⋅ sen α
) ⋅ (10 ) = 45 ⋅ 10
2 ⋅ 10 ⋅ sen(30º )
−12
JJJG
Fm
−4
JJG
F ⇔ C = 45 pF
Fy
Pelo triângulo de forças, temos:
JJG JJG
Fm = N ⋅ cos 45º =
QUESTÃO 05
2 2
⋅
= 0,25 N
4 2
O campo magnético B no interior do solenóide tem módulo dado por:
⎛ 4π ⋅ 10 −7 ⎞ 103
⎛μ ⎞
= 0,5 T
B = n ⋅ ⎜ 0 ⎟ ⋅ i cilindro = 1000 ⋅ ⎜
⎟⋅
⎝ h ⎠
⎝ 0,8 ⎠ π
Já pela lei de Faraday-Neumann, a corrente iB induzida na barra (que
fecha um circuito com a armação em “U”) é calculada como:
B ⋅ d ⋅vx
ΔΦ
ΔA
Δx
ε=
⇔ R ⋅ iB = B ⋅
= B ⋅d ⋅
= B ⋅ d ⋅ v x ⇔ iB =
Δt
Δt
Δt
R
Como o prisma tem faces triangulares com ângulos de 45°, a
velocidade vx de deslocamento da barra na direção horizontal deve ser
a mesma velocidade vertical v de subida do elevador. Assim:
B ⋅ d ⋅ v 0,5 ⋅ 0,25 ⋅ v v
iB =
=
=
1
8
R
JJG
Da expressão para o módulo da força magnética Fm que atua sobre a
barra, concluímos que:
JJG
v
Fm = B ⋅ i B ⋅ d ⋅ sen90° ⇔ 0,25 = 0,5 ⋅ ⋅ 0,25 ⋅ 1 ⇔ v = 16 m/s
8
4
OS MELHORES GABARITOS DA INTERNET: www.elitecampinas.com.br
O ELITE RESOLVE IME 2011 – FÍSICA DISCURSIVAS
(19) 3251-1012
QUESTÃO 06
Substituindo T0 − T3 =
Mas como T0 − T1 =
6
⋅ (T0 − T1 ) , vem que:
5
φ ⋅e φ ⋅e
6
⋅ (T0 − T1 ) = 2 f + 2 i
5
kf ⋅ A k i ⋅ A
φ1 ⋅ ef
,
kf ⋅ A
ki =
4
1
kf =
kf
100
25
e a condição do
enunciado é que a transferência de calor fique igual a 20% da original
20
⎛
⎞
⎜ φ2 = 100 φ1 ⇔ φ1 = 5φ2 ⎟ , temos:
⎝
⎠
φ ⋅e
6 φ1 ⋅ ef φ2 ⋅ ef φ2 ⋅ ei
6 (5φ2 ) ⋅ ef φ2 ⋅ ef
⋅
=
+
⇔ ⋅
=
+ 2 i ⇔
5 kf ⋅ A k f ⋅ A k i ⋅ A
5
kf
kf
⎛ 1 ⎞
⎜ kf ⎟
⎝ 25 ⎠
ei 1
=
5ef = 25ei ⇔
ef 5
Uma fábrica foi multada pela prefeitura local, pois a temperatura
externa da parede de um forno industrial encontrava-se em um nível
superior ao previsto pelas normas de segurança (Figura 1).
Para atender às normas recomenda-se o seguinte procedimento
(Figura 2):
A parede externa do forno deve ser recoberta com um material de
condutividade térmica igual a 4% da parede do forno. Isso faz com que
a transferência de calor fique igual a 20% da original e que a redução
de temperatura entre a superfície interna da parede do forno e a
superfície externa do isolante fique 20% maior que a situação inicial.
QUESTÃO 07
Determine a razão entre a espessura do isolante (ei) e a espessura da
parede do forno (ef).
Resolução
Num regime estacionário de condução, o fluxo de calor φ entre duas
superfícies de área A, espessura d e coeficiente de condutividade
térmica k, com diferença de temperaturas ΔT , é dado por:
k ⋅ A ⋅ ΔT
φ=
d
T0
T1
T0
T2
A figura acima mostra um corpo sólido cilíndrico de altura h, densidade
ρ e área da base A, imerso em um líquido de mesma densidade em
um tanque também cilíndrico com base interna de área 4A. A partir do
instante t = 0 (situação da figura), o líquido passa a ser bombeado
para fora do tanque a uma vazão variável dada por U (t ) = bAt , onde b
é uma constante positiva.
Dados:
• comprimento da corda entre os pontos B e C: L;
• densidade linear da corda entre os pontos B e C: μ;
• aceleração gravitacional local: g.
Observações:
• desconsidere o peso da corda no cálculo da tração;
• a tensão instantânea na corda é a mesma em toda a sua extensão.
Pede-se:
a) a expressão do nível y do líquido (onde y ≤ h) em função do tempo;
b) a velocidade v(t) de um pulso ondulatório transversal, partindo do
ponto B em t = 0, e sua respectiva posição x(t);
c) a razão L/h para que o pulso ondulatório transversal, partindo do
ponto B em t = 0, chegue até C no mesmo instante em que o nível do
líquido alcança o ponto E.
Resolução
a) Tomando U como sendo a variação do volume em um determinado
intervalo de tempo teremos:
ΔV ( 4 A − A ) ⋅ Δy
Δy
Δy
b
=
⇔ b ⋅ A ⋅ t = 3A ⋅
⇔
= vy = ⋅ t
U=
3
Δt
Δt
Δt
Δt
Pode-se concluir então que vy cresce com aceleração constante e
igual a b/3. Assim:
a ⋅ t2
b ⋅ t2
b ⋅t2
y (t ) = y0 + v0y ⋅ t + y
= 0 + 0⋅t +
⇔ y (t ) =
6
2
6
b) Observe que o módulo da tensão T na corda corresponde ao
módulo do peso da parte emersa do sólido, visto que o peso da parte
imersa será anulado pelo empuxo (uma vez que o corpo e o líquido
têm a mesma densidade):
JG
bt 2
T = ρ ⋅ g ⋅ [ A ⋅ y (t )] = ρ ⋅ g ⋅ A ⋅
6
A velocidade do pulso ondulatório na corda de densidade linear μ, e
submetida a uma tensão T, é dada por:
JG
ρ⋅g ⋅ A⋅b
T
ρ ⋅ g ⋅ A ⋅ b ⋅t2
v=
=
⇔ v =t
6μ
6μ
μ
T3
Vamos chamar de:
• T0 a temperatura interna do forno (ambas as situações);
• T1 a temperatura externa sem isolante (figura 1);
• T2 a temperatura na junção entre a parede do forno e o isolante
(figura 2);
• T3 a temperatura externa com isolante (figura 2).
Como a redução de temperatura entre a superfície interna da parede
do forno e a superfície externa do isolante deve ficar 20% maior que a
situação inicial, escrevemos:
20 ⎞
6
⎛
T0 − T3 = ⎜ 1 +
⎟ ⋅ (T0 − T1 ) ⇔ T0 − T3 = ⋅ (T0 − T1 )
5
⎝ 100 ⎠
Na figura 1, o fluxo de calor na parede do forno, no regime
estacionário, é dado por:
k ⋅ A ⋅ (T0 − T1 )
φ ⋅e
φ1 = f
⇔ T0 − T1 = 1 f
ef
kf ⋅ A
Na figura 2, o fluxo de calor na parede do forno, no regime
estacionário, deve ser igual ao fluxo de calor no material isolante:
φ2 ⋅ ef
⎧
⎪T0 − T2 = k ⋅ A
kf ⋅ A ⋅ (T0 − T2 ) ki ⋅ A ⋅ (T2 − T3 )
⎪
f
φ2 =
=
⇔⎨
ef
ei
⎪T − T = φ2 ⋅ ei
3
⎪⎩ 2
ki ⋅ A
Somando essas duas equações membro a membro, vem que:
φ ⋅e φ ⋅e
φ ⋅e φ ⋅e
(T0 − T2 ) + (T2 − T3 ) = 2 f + 2 i ⇔ T0 − T3 = 2 f + 2 i
kf ⋅ A k i ⋅ A
kf ⋅ A k i ⋅ A
Disso concluímos então que a velocidade v(t) do pulso cresce com
aceleração constante e novamente aplicamos:
5
OS MELHORES GABARITOS DA INTERNET: www.elitecampinas.com.br
O ELITE RESOLVE IME 2011 – FÍSICA DISCURSIVAS
(19) 3251-1012
x ( t ) = x0 + v 0 x ⋅ t +
b) Seja P o ponto em que a leitura do voltímetro é zero. Para que isto
ocorra, a queda de tensão no ramo AP deve ser igual a queda de
tensão em R1:
U AP = U1
ax ⋅ t 2
ρ ⋅ g ⋅ A ⋅ b t2
⇒ x (t ) = 0 + 0 ⋅ t +
⋅ ⇔
2
6μ
2
x (t ) =
t2 ρ ⋅ g ⋅ A ⋅ b
⋅
2
6μ
Além disso, de acordo com a figura, temos: R '1 + R '2 = RAB , assim,
analogamente ao item (a):
R' ⋅E
R' ⋅E
U AP = 1 ⇒ U1 = 1
RAB
RAB
⎧ x (t ) = L
, para o mesmo instante de tempo t, temos:
c) Fazendo ⎨
⎩ y (t ) = h
t2 ρ ⋅ g ⋅ A ⋅ b
⋅
L
3⋅ρ⋅g ⋅ A
6μ
L x (t ) 2
=
=
⇔ =
h
2⋅μ⋅b
b ⋅t2
h y (t )
6
(Ι)
Sendo a resistência proporcional ao comprimento:
σ⋅A
R=
, onde σ é a resistividade, A a área da seção do resistor e A
A
seu comprimento, temos:
σ ⋅ yP ⎫
R '1 =
A ⎪⎪ Substituindo em (Ι )
⎬
σ⋅L⎪
R 'AB =
A ⎪⎭
⎛ σ ⋅ yP ⎞
⎜ A ⎟
⎠ ⋅ E ⇒ U = y P ⋅ E ⇒ 2,5 = y P ⋅ 10
U1 = ⎝
1
L
L
⎛ σ⋅L ⎞
⎜
⎟
⎝ A ⎠
QUESTÃO 08
L
,onde L é o comprimento do resistor AB.
4
c) Diagrama de forças do balão:
JG
JG JG
F R = P + E ⇒ FR = P − E ⇒
E
m ⋅ a = m ⋅ g − ρ ⋅ g ⋅V ⇒
ρ ⋅ g ⋅V
50 ⋅ 10 ⋅ 0,0001
= 10 −
a=g−
m
0,05
P
yP =
O circuito apresentado na figura acima é composto por uma fonte de
tensão contínua E, que alimenta um reostato linear e as resistências
R1 e R2. No ponto C do reostato encontra-se fixo um balão de massa
m e volume V, inicialmente na posição y = 0. O sistema encontra-se
imerso em um tanque, que contém um líquido isolante, de massa
específica ρ. Entre os pontos C e D do sistema, encontra-se
conectado um voltímetro ideal. No instante t = 0, o balão é liberado e
começa a afundar no líquido.
Determine:
a) a leitura do voltímetro no instante em que o balão é liberado;
b) a coordenada y em que a leitura do voltímetro é zero;
c) o tempo decorrido para que seja obtida a leitura indicada no item b;
d) o valor da energia, em joules, dissipada no resistor R2, no intervalo
de tempo calculado em c.
Dados:
• R1 = 1 kΩ;
• R2 = 3 kΩ;
• fonte de tensão: E = 10 V;
• massa do balão: m = 50 g;
• volume do balão: V = 0,0001 m3;
• resistência total do resistor linear: RAB = 10 kΩ;
• massa específica do líquido: ρ = 50 kg/m3;
• aceleração da gravidade: g = 10 m/s2.
Resolução
Veja a figura:
a = 9 m / s²
L
, temos um MRUV, assim podemos escrever:
4
a ⋅ Δt 2
L
9 ⋅ Δt 2
y = y 0 + v 0 ⋅ Δt +
⇒ = 0 + 0 ⋅ Δt +
2
4
2
De y 0 = 0 a y =
Δt =
1 L
s ,onde o valor de L é dado em metros.
3 2
d) Sejam P2 e ε
respectivamente:
a potência e a energia dissipadas em R2,
2
P2 = R2 ⋅ i D2 ⇒
⎛ E ⎞
ε
= R2 ⋅ ⎜
⎟ ⇒
Δt
⎝ R1 + R2 ⎠
2
⎛ E ⎞
1 L
10
⎛
⎞
ε = Δt ⋅ R2 ⋅ ⎜
⋅ 3000 ⋅ ⎜
⎟ = ⋅
⎟
3 2
⎝ 1000 + 3000 ⎠
⎝ R1 + R2 ⎠
ε=
2
L
1
⋅
J , onde L é dado em metros.
160 2
QUESTÃO 09
R’1
R’2
P
iD
iP
a) Seja U1 a leitura do voltímetro:
R ⋅E
1000 ⋅ 10
⎪⎧U1 = R1 ⋅ i D
⇒ U1 = 1
=
⎨
R1 + R2 1000 + 3000
⎪⎩E = (R1 + R2 ) ⋅ i D
U1 = 2,5V
NOTA: Esta questão pecou por não fornecer o comprimento total do
reostato, assim, acreditamos que os itens b), c) e d) devem ser
anulados, contudo, faremos a seguir a resolução destes itens e os
colocaremos em função do comprimento total do reostato, o qual
chamaremos de L.
A Figura mostra dois raios luminosos r1 e r2, de mesma frequência e
inicialmente com diferença de fase δ1, ambos incidindo
perpendicularmente em uma das paredes de um reservatório que
contém líquido. O reservatório possui uma fenda de comprimento h
6
OS MELHORES GABARITOS DA INTERNET: www.elitecampinas.com.br
O ELITE RESOLVE IME 2011 – FÍSICA DISCURSIVAS
(19) 3251-1012
preenchida pelo líquido, na direção de r2. Determine o comprimento da
fenda para que a diferença de fase medida no Detector D entre os
raios seja δ2.
O carrinho D desloca-se com velocidade de 60 m/s na direção do
carrinho E, que está parado. O corpo A possui uma carga elétrica
idêntica à armazenada em um circuito capacitivo e está apoiado sobre
o carrinho E, conforme a figura acima. Dá-se a colisão dos dois
carrinhos, com um coeficiente de restituição igual a 0,9. Após alguns
segundos, o carrinho E para bruscamente e o corpo A penetra em
uma região em que existe um campo magnético uniforme normal ao
plano da figura, que o faz descrever um movimento helicoidal de raio
4,75 m. Desprezando o efeito da massa de A na colisão, determine a
massa do carrinho E.
Dados:
• massa do carrinho D: mD = 2 kg;
• massa do corpo A: mA = 4 × 10–6 kg;
• campo magnético: B = 16 T.
Resolução
A carga armazenada no circuito capacitivo, que corresponde a uma
associação em série dos capacitores, é dada por:
⎛ C ⋅C ⎞
⎛ 0,6 ⋅ 10 −6 ⋅ 1,2 ⋅ 10 −6 ⎞
Q = CEQ ⋅ U = ⎜ 1 2 ⎟ ⋅ U = ⎜
⋅ 5 = 2 ⋅ 10 −6 C
−6
−6 ⎟
⎝ 0,6 ⋅ 10 + 1,2 ⋅ 10 ⎠
⎝ C1 + C2 ⎠
Dados:
• índice de refração do líquido: n;
• índice de refração da parede do reservatório: nR;
• comprimento de onda dos raios luminosos no ar: λ.
Observação:
• considere o índice de refração da parede do reservatório maior que o
índice de refração do líquido.
Resolução
A defasagem do raio 2 na fenda pode ser obtida por uma simples
regra de três, considerando que o comprimento de onda em um meio
λ
, onde λ é o comprimento de onda no
de índice de refração n é
n
vácuo (que é aproximadamente o mesmo do ar):
h
Δφ
2πh
⇒ Δφ =
⋅n
λ
2π
λ
n
Observe a figura:
Vamos supor que a carga elétrica do corpo A seja positiva e de
mesmo módulo que essa carga armazenada no circuito, isto é:
QA = +2 ⋅ 10 −6 C
Com relação ao movimento dessa carga no campo magnético, temos
as seguintes ressalvas:
(I) Embora o enunciado não deixe claro, por não mencionar em
momento algum a atuação de um campo gravitacional,
consideraremos que, nesta questão, tal campo não exista.
Caso contrário seu valor deveria ter sido fornecido no enunciado. A
ausência dessa informação tornaria inviável a resolução da questão.
(II) Como o vetor velocidade do corpo A estará necessariamente no
plano da folha durante todo o movimento e, portanto, sempre
perpendicular ao campo magnético, não há nenhuma possibilidade de
o corpo executar um movimento helicoidal. Se pudermos considerar a
inexistência de campo gravitacional neste problema, esse movimento
será circular uniforme enquanto o corpo estiver dentro da região em
que atua o campo magnético.
Assumindo então o movimento circular uniforme na região do campo
magnético, com raio R = 4,75 m , temos que a força magnética atua
como resultante de natureza centrípeta. Assim:
JJG JJJG
m ⋅ v A2
FM = FCP ⇔ QA ⋅ v A ⋅ B ⋅ sen90° =
⇔
R
Q ⋅ B ⋅ R 2 ⋅ 10 −6 ⋅ 16 ⋅ 4,75
vA = A
=
= 38 m/s
m
4 ⋅ 10 −6
Supondo que essa velocidade fosse também a velocidade do carrinho
E logo após a colisão (enquanto o corpo A estava apoiado nele), do
coeficiente de restituição temos que:
v '− v D '
38 − v D '
⇔ 0,9 =
⇔ v D ' = −16 m/s
e= E
vD − vE
60 − 0
L1
L2
Sejam as fases dos dois raios dadas por ϕ . Neste caso, temos que as
fases finais dos raios 1 e 2 são dadas, respectivamente, por:
2πh
⎧
+ Δϕ
⎪ϕ1f = ϕ1 + λ
⎪⎪
nR
, onde:
⎨
⎪ϕ = ϕ + 2πh + Δϕ
2
⎪ 2f
λ
⎪⎩
n
Δϕ é a defasagem correspondente às distâncias L1 e L2 e é igual para
os dois raios. Assim, para determinar a relação entre as defasagens e
h, basta fazer a diferença entre as duas equações. Contudo, não foi
dado no enunciado qual é a referência de sinal para as defasagens,
isto é:
⎧⎪δ1 = ϕ1 − ϕ2
⎧⎪δ = ϕ2 − ϕ1
ou ⎨ 1
⎨
⎪⎩δ2 = ϕ1f − ϕ2f
⎪⎩δ2 = ϕ2f − ϕ1f
Com isto, esperamos que o IME considere qualquer uma das
hipóteses. Salientamos, porém, que a falta desta informação pode ter
prejudicado alguns candidatos. Fazendo a diferença das equações
com a consideração acima, temos:
2πh
2πh
( ϕ1f − ϕ2f ) = ( ϕ1 − ϕ2 ) +
( nR − n ) ⇒ ±δ2 = ±δ1 +
( nR − n ) ⇒
λ
λ
h=±
Assim, impondo a conservação da quantidade de movimento do
sistema na colisão, vem que:
mD ⋅ v D + mE ⋅ v E = mD ⋅ v D '+ mE ⋅ v E ' ⇔
2 ⋅ 60 + mE ⋅ 0 = 2 ⋅ ( −16) + mE ⋅ 38 ⇔ mE = 4 kg
λ ( δ2 − δ1 )
⋅
2π ( nR − n )
Equipe desta resolução
Física
QUESTÃO 10
Danilo José de Lima
Luís Salles de Carvalho
Vinício Merçon Poltronieri
Revisão
Eliel Barbosa da Silva
Fabiano Gonçalves Lopes
Marcelo Duarte Rodrigues Cecchino Zabani
Vagner Figueira de Faria
Digitação, Diagramação e Publicação
Carolina Marcondes Machado
Guilherme Coelho Ranulfi
7