Análise de Correlações Intra e Inter-Classe em Dados de - IME-USP

Análise de Correlações Intra e Inter-Classe em Dados de Famílias Projeto Corações de Baependi, MG
Tatiana Martorano Bona1
Suely Ruiz Giolo2,3
Júlia Maria Pavan Soler1 (Orientadora)
indivíduos e seus familiares, estendendo os
graus de parentesco tanto quanto possível
para inclusão de relacionamentos verticais
(ao longo de gerações, pais, filhos, netos) e
horizontais (tios, sobrinhos, primos).
Almasy e Blangero (1998) e de Andrade et
al. (1999) apresentam um modelo de
componentes de variância para obtenção de
estimativas de herdabilidade na análise
genética de dados de famílias. O coeficiente
de herdabilidade, definido na área de
Genética, nada mais é que o coeficiente de
correlação intra-classe sob a formulação de
um modelo misto, representando a
proporção da variância total que é devida a
fatores genéticos. Desse modo, uma
alternativa tem sido obter estimativas de
correlações intra e inter-classe via o ajuste
de modelos mistos a dados de famílias. No
caso de correlações entre diferentes
variáveis em dados de famílias, o modelo
misto multivariado (Amos et al., 2001;
Kullo et al., 2005) pode ser adotado para
obtenção das estimativas de correlações.
Sob modelos mistos, Khoury et al. (1993) e
Thomas
(2004)
introduzem
uma
representação das correlações familiares a
partir de diagramas de caminhos. Para
variáveis de sobrevivência, como a idade de
diagnóstico de hipertensão, por exemplo,
que seguem, em geral, uma distribuição
assimétrica e com a presença de censuras,
Wintrebert et al. (2006) apresentam uma
formulação em termos dos resíduos
martingale do modelo de Cox para obtenção
de estimativas da correlação genética.
Pankratz et al. (2004) introduz o modelo de
Cox com efeito aleatório genético na
análise de fenótipos de sobrevivência.
No presente trabalho são considerados os
dados do projeto Corações de Baependi,
MG, que envolve famílias brasileiras. São
realizadas análises de correlação inter e
intra-classe, uni e multivariada, para
diferentes variáveis do estudo tais como:
pressão sistólica e diastólica, c-LDL,
glicose e idade de diagnóstico de
hipertensão, diabetes e colesterol elevado,
visando descrever as relações familiares e
encontrar evidências da participação de
1
Instituto de Matemática e Estatística Universidade de São Paulo
2
Universidade Federal do Paraná
3
Instituto do Coração
1. Introdução
O estudo relacionando genes como fatores
de risco para doenças é uma importante
área da Epidemiologia e acredita-se que o
conhecimento dessa associação contribua
para que novos critérios de prevenção,
diagnóstico e tratamento de doenças sejam
estabelecidos. A maioria das doenças de
interesse em saúde pública, tais como a
hipertensão, diabetes e depressão, são
decorrentes de um complicado mecanismo
de regulação envolvendo componentes
ambientais, genéticos e suas possíveis
interações. O mapeamento genético de tais
doenças, no sentido de identificar os genes
envolvidos tem, atualmente, sido alvo de
muitos estudos.
Um dos primeiros passos no mapeamento
genético de doenças é encontrar evidências
de que há componentes genéticos
associados à etiologia ou regulação das
mesmas.
Alternativas úteis para esta
finalidade são as análises de correlação
intra-classe (devido à estrutura familiar, por
exemplo) e correlações inter-classe (entre
graus de parentesco), as quais podem ser
formuladas sob um contexto uni ou
multivariado, dependendo das variáveis
consideradas.
Delineamentos com famílias têm sido
usados com sucesso no mapeamento de
genes de doenças comuns, como o projeto
Northern Manhattan Family Study, que
investigou a herdabilidade da síndrome
metabólica em 89 famílias caribenhashispânicas, ou o projeto San Antonio
Family Heart Study que considerou uma
amostra de famílias americanas mexicanas.
Nestes estudos, dados foram coletados em
309
componentes genéticos na variação das
respostas entre os indivíduos.
em que µ é media fenotípica geral, β j ’s
são coeficientes de regressão associados às
covariáveis definidas na matriz X = ( X ij )
2. Material
e, g i e ei são variáveis aleatórias
representando o efeito poligênico e residual,
respectivamente. Os efeitos aleatórios, g i e
Entre Dezembro de 2005 e Janeiro de 2006,
foi selecionado um total de 1.712
indivíduos de 119 famílias do município de
Baependi, uma cidade com características
predominantemente rurais localizada no
Estado de Minas Gerais. Dos 20 setores
censitários
(IBGE-2000)
nos
quais
Baependi é dividida, 11 deles foram
selecionados aleatoriamente para o estudo.
Dentro de cada setor sorteado, domicílios
foram selecionados por amostragem
sistemática (com fator 20). Um residente
maior de 18 anos foi, então, convidado a
responder um questionário familiar e a
participar do estudo. Indivíduos que
aceitaram o convite, juntamente com todos
os seus parentes e cônjuges, foram
convidados para avaliação física, clínica e
laboratorial. Além disso, amostras de
sangue de todos os indivíduos foram
coletadas e armazenadas, bem como o seu
DNA.
Do total de dados coletados, 1.675
indivíduos de 81 famílias constituíram a
amostra sob análise. Famílias de apenas
dois indivíduos foram excluídas por serem
pouco informativas para os objetivos do
presente estudo. O tamanho das famílias
variou de 3 a 156 indivíduos (tamanho
médio de 21 indivíduos). A média de idade
foi de 44 anos, variando de 18 a 100 anos.
A distribuição da amostra quanto ao sexo
foi de 56,5% de mulheres e 43,5% de
homens.
ei , são assumidos não-correlacionados e
normalmente distribuídos com média zero e
2
2
variância σ g e σ e , respectivamente. Em
geral, o componente residual é suposto
comum a cada indivíduo, enquanto o
componente poligênico é compartilhado
entre indivíduos, sendo proporcional ao seu
grau de parentesco. A matriz de
covariâncias entre as variáveis fenotípicas
para os indivíduos i e i´ é dada por:
2
2

σ g + σ e para i = i ' ,

2
Cov( yi ; yi′ ) = 2φii 'σ g para i ≠ i ' , mas relacionados,
 0 para i ≠ i ' e não − relacionados.

(2)
2φ ii '
em que
é o coeficiente de
relacionamento entre os indivíduos i e i‘. A
função de verossimilhança considerando os
dados dos membros de uma família é, em
geral, obtida a partir da distribuição normal
multivariada. A herdabilidade poligênica ou
devida à agregação familiar é estimada por
hˆg2 = σˆ g2 /(σˆ g2 + σˆ e2 ) . Considerando graus
de parentesco específicos, pode-se estimar
as correlações inter-classes a partir da
expressão (2), com 2φii ' substituído por seu
correspondente valor, tal que:
2
Cov( yi ; yi′ ) 2φii 'σˆ g
=
= 2φii ' hˆg2 .(3)
2
2
σˆ Y
σˆ Y
3. Métodos
ρˆ gii ' ( yi ; y i′ ) =
O modelo de componentes de variância tem
sido adotado na literatura para obtenção de
estimativas de herdabilidade poligênica em
estudos com famílias, sendo a herdabilidade
definida como a proporção da variância
total que é devida a componentes genéticos
(coeficiente de correlação intra-classe). Sob
tal modelo, a variável fenotípica observada
no indivíduo i, denotada por yi, é modelada
por:
Os casos de maior interesse são para
correlações genéticas entre pais e filhos
( 2φ ii ' =
2
)
e
entre
avós
e
netos
( 2φii ' = 4 ).
Havendo interesse em
correlações dependentes do sexo, pode-se
formular o modelo (1) com efeitos
genéticos específicos a cada sexo, de tal
forma que a matriz de covariâncias fica
expressa por:
1
c
y i = µ + ∑ β j X ij + g i + ei
1
(1)
j =1
310
2
σ gF
+ σ e2 para i = i' e ambos fem,
 2
2
σ
 gM + σ e para i = i' e ambos masc,
2φ σ 2
 ii ' gF para i ≠ i' , relacionados, e ambos fem,
Cov( yi ; yi ′ ) = 
2
2φii 'σ gM para i ≠ i' , relacionados, e ambos masc,

2
φ
σ
 ii ' gF σ gM para i ≠ i ' , relacionados, um fem e outro masc,
0 para i ≠ i' e não − relacionados.
correlações genéticas e ambientais, dadas
por:
ρˆ g12 ( y i1 ; y i′ 2 ) =
(4)
O ajuste do modelo (1) com matriz de
covariâncias dada em (4) permite que sejam
obtidas estimativas de herdabilidades e
correlações inter-classe para cada nível do
fator sexo. Deste modo, pode-se estudar,
por exemplo, se o padrão de dependência
das respostas entre pais e filhos é diferente
daquele entre mães e filhos.
Considerando modelos mistos como em (2)
ou (4), testes de hipóteses sobre
herdabilidades e coeficientes de correlação
podem ser realizados com base na
estatística razão de verossimilhanças que,
sob condições de regularidade, tem uma
distribuição mistura de qui-quadrados.
No caso de correlações envolvendo
diferentes
variáveis
observadas
em
membros familiares, o modelo (1) pode ser
estendido para o caso multivariado (Amos
et al., 2001; Kullo et al., 2005) e, a partir
deste, estimativas das correlações são
obtidas.
Neste
caso,
considerando
ρˆ e12 ( y i1 ; y i′ 2 ) =
,
σˆ g21 σˆ g2 2
σˆ e12
σˆ e21 σˆ e22
.
(6)
Correlações fenotípicas entre duas variáveis
podem ser calculadas com base nas
correlações genéticas e ambientais do par
de variáveis. Uma estimativa da correlação
fenotípica entre duas variáveis é obtida pela
expressão:
ρˆ 12 ( y i1 ; y i′ 2 ) = ρˆ g12 hˆg21 hˆg2 2 + ρˆ e12 hˆe21 hˆe22 (7)
A estimativa ρ̂12 é similar ao coeficiente de
correlação de Pearson e tem a vantagem de
ser uma estimativa não viciada da
correlação fenotípica em dados de família
(Kullo et al., 2005). Além disso, a
2
correlação genética ao quadrado ρˆ g 12 entre
duas variáveis é considerada a variância
genética aditiva nas duas variáveis que é
devida a efeitos de genes compartilhados
(genes comuns que controlam ambas as
variáveis) e pode ser interpretada como uma
medida de efeitos pleiotrópicos de genes
influenciando
ambos
os
traços
simultaneamente.
′
Y f = (Y f 1 , Y f 2 ) o vetor de respostas para
duas variáveis de interesse observadas nos
indivíduos da f-ésima família, a matriz de
covariâncias associada ao modelo misto
multivariado definido em termos de (1) é
dada por:
Neste trabalho, o ajuste de modelos de
componentes de variância e estimativas de
herdabilidades e correlações considerando
os dados Baependi são obtidos com o apoio
do aplicativo SOLAR (www.sfbr.org) e dos
pacotes Kinship e Multic do R.
Ω f = A2×2 ⊗ 2Φ f + B2×2 ⊗ I f ,
A2×2
σˆ g12
(5)
2
 σ g21 σ g12 
σ
σ e12 
, B2×2 =  e1

=
2 
2 

σ
σ
σ
σ
g
12
g
2
12
2
e
e




No caso da análise de fenótipos de
sobrevivência censurados, como o da idade
de diagnóstico, não é possível calcular as
correlações a partir dos métodos
apresentados anteriormente, visto que a
distribuição desses fenótipos é, em geral,
assimétrica e há a presença de censuras.
Assim, para tais estimativas, usaremos os
resíduos martingale do modelo de Cox,
como proposto por Wintrebert et al. (2006).
O modelo de Cox assume uma função risco
para cada indivíduo i na família j em que o
risco da doença na idade t é expresso por:
em que A e B contêm os componentes de
variância e covariância, poligênico e
residual, respectivamente; a matriz 2Φ f
contém os coeficientes dos graus de
parentesco entre os indivíduos da família f
e If é a matriz identidade de ordem nf. O
símbolo ⊗ representa o produto direto de
duas matrizes. Sob o modelo misto com
matriz de covariâncias dada em (5), para a
variável m sob estudo (m = 1,2) pode-se
2
calcular a herdabilidade h gm e para cada
par de variáveis (Y1, Y2) pode-se calcular as
λij (t X ) = λ0 (t ) exp(βX ij )
311
(9)
respectivamente, e ρ representa a correlação
genética.
em que, X é o vetor de covariáveis
(essencialmente) ambientais, β corresponde
ao vetor dos coeficientes de regressão e λ0
é a função de risco basal. A partir desse
modelo, podemos calcular os resíduos
martingale, os quais serão usados na
estimação da correlação de indivíduos com
a mesma distância genética. Esses resíduos
são definidos por:
Figura1
X
ρg
g
gM
gF
e
eF
X
eM
Y
Y
g1
ˆ ,
(10)
MRi = δ i − Λ
i
ˆ = ∫t λ (u )du = exp(βX )Λ (t ) ,
com Λ
i
i
0
0 i
g2
ρ12
e1
e2
Y2
Y1
sendo δi a variável indicadora da censura,
ou seja, δi = 0 se ti corresponde a um tempo
X
Os resultados dos ajustes são apresentados
a seguir.
censurado e δi = 1, em caso contrário, e Λ̂ i
é uma estimativa do risco acumulado para o
indivíduo i.
Obtendo esse resíduo, assumimos que
eliminamos a correlação ambiental e
poderemos, então, obter as correlações
genéticas de interesse. Para tal análise,
faremos gráficos de dispersão entre
fenótipos de indivíduos de uma mesma
família com distância genética dada pelo
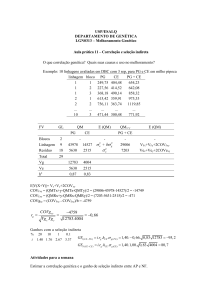
Quadro 1 - Correlação intra-classe (sem
estratificação): Estimativas da herdabilidade
poligênica devido à agregação familiar.
SPB
DBP
GLIC
LDL
Modelo 1
0,154
0,149
0,304
0,264
Modelo 2
0,271
0,211
0,327
0,267
coeficiente de relacionamento 2φii ' , em
Quadro 2 - Correlação intra-classe (estratificado
por sexo): Modelo 1.
particular com distâncias ½ e ¼.
Correlações intra-classe entre os resíduos
martingale do modelo de Cox serão, então,
obtidas para os pares de indivíduos com as
distâncias genéticas citadas.
4. Resultados preliminares
Inicialmente, transformação logarítmica das
variáveis: pressão sistólica (SBP), diastólica
(DBP), glicose (GLIC) e nível LDL de
colesterol, foi necessária com o objetivo de
satisfazer a suposição de normalidade
assumida pelos modelos mistos ajustados
(Expressão 1). Em cada caso, foram
considerados: Modelo 1 - sem covariáveis
(apenas com a média geral) e Modelo 2 incluindo as covariáveis sexo, idade, IMC e
o termo de interação sexo*idade. Até o
momento foram obtidas as correlações: (a)
intra-classe, (b) intra-classe estratificada
por sexo e (c) inter-classe (duas variáveis
em questão). A Figura 1 apresenta uma
representação em diagramas de caminhos
dos modelos de componentes de variância
genéticos ajustados, onde X representa as
covariáveis, Y os fenótipos, g e e as
herdabilidades genética e ambiental,
Y
2
hgF
2
hgM
ρ
2
heF
2
heM
SBP
DBP
GLIC
LDL
0,32
0,23
0,42
0,44
0,41
0,38
0,37
0,33
0,32
1,00
0,94
0,81
0,69
0,77
0,58
0,56
0,60
0,62
0,63
0,67
Quadro 3 - Correlação intra-classe (estratificado
por sexo): Modelo 2.
Y
2
hgF
2
h gM
ρ
2
heF
2
heM
SBP
DBP
GLIC
LDL
0,37
0,30
0,44
0,43
0,41
0,40
0,39
0,35
0,89
1,00
0,91
0,79
0,64
0,70
0,56
0,57
0,59
0,60
0,61
0,65
Quadro 4 - Correlação Genética Inter-Classe:
Modelo 1
SBP
DBP GLIC
LDL
SBP
0,154 0,874 0,152
-0,298
DBP
0,149 0,194
-0,361
GLIC
0,304
0,250
LDL
0,264
Na diagonal tem-se
312
h g2
e fora dela
ρg .
Quadro 6 – Estimativa das herdabilidades
utilizando resíduos martingale:
BP
GLIC
LDL
Quadro 5 – Correlação Genética Inter-Classe:
Modelo 2
SBP
DBP GLIC
LDL
SBP
0,271 0,890 0,170
-0,197
DBP
0,211 0,241
-0,250
GLIC
0,327
0,245
LDL
0,267
0,169
0,144
0,113
Estes resultados indicam que para a
população em estudo o efeito genético é
alto para os fenótipos quantitativos
analisados e pouco pronunciado para as
idades de diagnóstico. Porém, devemos
salientar que a hipótese de normalidade
testada via estatística de Shapiro foi
rejeitada paras as três variáveis (p-valor <
2.2e-16). A Figura 2 apresenta seus
respectivos gráficos de normalidade:
ρg .
Os resultados do Quadro 1 indicam que as
correlações genéticas para os dados sob
análise se situam entre 0,14 e 0,33 e que o
efeito da inclusão de covariáveis no valor
da correlação depende da variável em
questão. O mesmo fato pode ser observado
nos Quadros 2 e 3, pois dependendo das
covariáveis adicionadas os resultados
variam. Comparando o Quadro 1 com o 2 e
3, podemos ver que quando estratificamos
por sexo as herdabilidades, genética e
ambiental, tendem a aumentar para todas as
variáveis, indicando que tais doenças
possuem um padrão de dependência das
respostas entre pais e filhos diferente
daquela entre mães e filhas.
No que diz respeito ao coeficiente de
correlação genético entre os sexos,
podemos ver, com exceção da variável SBP
no ajuste sem covariáveis (Quadro 2), que
há forte correlação positiva entre os sexos
para uma mesma variável ( ρ̂ entre 0,79 e
1,00) e que o possível efeito de interação
genética versus sexo é explicado pelos
componentes de variância, os quais
mostram uma certa heterocedasticidade.
Pelos Quadros 4 e 5, podemos observar,
que a correlação genética entre as variáveis
relacionadas com a hipertensão (SBP e
DPB) é alta (0,87 e 0,89), enquanto que
entre as outras variáveis o módulo máximo
de correlação não ultrapassou o valor de
0.36.
Além disso, é possível notar que as
variáveis SBP, DPB e GLIC, são
correlacionadas positivamente entre si. O
mesmo ocorre entre GLIC e LDL. Porém,
entre SBP e LDL e DPB e LDL temos que a
correlação genética é negativa.
Estas estimativas estão de acordo com as de
outros estudos apresentados na literatura
considerando diferentes populações.
A partir dos resíduos martingale, também
foram calculadas herdabilidades utilizando
o modelo 1 descrito anteriormente:
Figura 2
-1
-3
-2
Quantis Amostrais
0
1
Gráfico QQ dos Resíduos Martingale para Variável Pressão
-3
-2
-1
0
1
2
3
Quantis Teóricos
0.0
-1.0
-0.5
Quantis Amostrais
0.5
1.0
Gráfico QQ dos Resíduos Martingale para Variável Glicose
-3
-2
-1
0
1
2
3
Quantis Teóricos
-0.5
Quantis Amostrais
0.5
1.0
Gráfico QQ dos Resíduos Martingale para Variável Colesterol
0.0
2
Na diagonal tem-se h g e fora dela
Modelo 1
-3
-2
-1
0
1
2
3
Quantis Teóricos
Como gostaríamos, fizemos gráficos de
dispersão entre fenótipos de indivíduos de
313
uma mesma família com distância genética
dada
pelo
coeficiente
de
de parentesco entre os indivíduos,
sugerindo a não existência de componentes
genéticos associados a estas variáveis de
sobrevivência.
relacionamento 2φii ' , em particular com
distâncias ½ e ¼ e também calculamos as
correlações de Pearson de cada um dos
gráficos. A Figura 3 apresenta o gráfico de
dispersão dos resíduos para ambas as
medidas de distância considerando os dados
de hipertensão. Para os demais fenótipos
um padrão semelhante foi encontrado. O
Quadro 7 mostra os coeficientes de
correlação para os resíduos de acordo com
os fenótipos e as distâncias genéticas
estudadas.
Agradecimentos
Ao CNPq o suporte financeiro (Bolsa
PIBIC/IME-USP) concedido.
Referências
[1]
Almasy L, Blangero J. (1998)
Multipoint quantitative-trait linkage
analysis in general pedigrees. Am J
Hum Genet 62:1198-211.
[2] de Andrade M, Amos CI, Thiel TJ.
(1999) Methods to estimate genetic
components of variance for quantitative
traits in family studies. Genet
Epidemiol, 17:64-76.
[3] Amos C, de Andrade M, Zhu D.(2001)
Comparison of multivariate tests for
genetic linkage. Hum Her,51:133-144.
[4] Colosimo E. A., Giolo S. R. (2006)
Análise de Sobrevivência Aplicada.
ABE – Projeto Fisher.
[5] Khoury MJ, Beaty TH, Cohen B. (1993)
Fundamentals
of
Genetic
Epidemiology. Oxford: Univ Press.
[6] Kullo IJ, Turner ST, Kardia SLR,
Mosley TH, Boerwinkle E., de Andrade
M. (2006). A genome-wide linkage
scan for ankle-brachial index in African
American and non-Hispanic white
subjects participating in the GENOA
study. Atherosclerosis,187(2):433-8.
[7] Pankratz V.S., de Andrade M.,
Therneau T. M. (2004) Random-Effects
Cox Proportional Hazards Model:
General Variance Components Methods
for Time-to-Event Data. Genetic
Epidemiology, 28: 97-109
[8] Thomas D. (2004). Statistical Methods
in Genetic Epidemiology. Oxford:
Oxford University Press.
[9] Wintrebert C. M. A., Zwinderman A.
H., Maat-Kievit A., Roos R. A.,
Houwelingen H.C. (2006) Assessing
genetic effects in survival data by
correlating martingale residuals with an
application to age at onset of
Huntington disease. Statistics in
Medicine, 25: 3190-3200.
Figura 3
-3
-2
-1
Indivíduo 2
0
1
Gráfico de Dispersão para Hipertensão de Indivíduos com
Distância Genética 0.5
-2
-1
0
1
Indivíduo 1
-1
-3
-2
Indivíduo 2
0
1
Gráfico de Dispersão para Hipertensão de Indivíduos com
Distância Genética 0.25
-2.5
-2.0
-1.5
-1.0
-0.5
0.0
0.5
1.0
Indivíduo 1
Quadro 7 – Correlação de Pearson para os
resíduos martingales.
Correlação de Pearson
Hipertensão (½)
0,097
Colesterol (½)
0,059
Diabetes (½)
0,079
Hipertensão (¼)
0,040
Colesterol (¼)
0,009
Diabetes (¼)
0,042
A partir dos gráficos da Figura 3 e das
correlações apresentadas no Quadro 7,
podemos observar que o padrão de
dispersão dos resíduos martingales não
indica altas correlações em função do grau
314