Física - Anglo

Treinamento para
Olimpíadas de
1 ª- / 2 ª- s é r i e E M
Física
2008
www.cursoanglo.com.br
AULAS 5 e 6
MOVIMENTO CIRCULAR
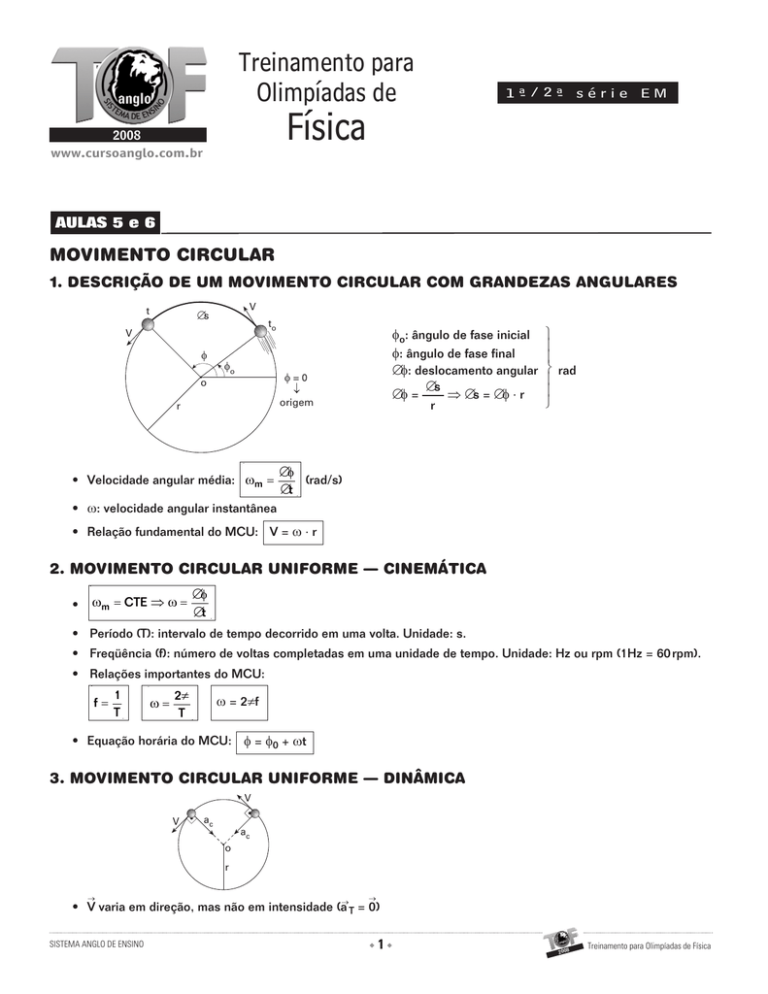
1. DESCRIÇÃO DE UM MOVIMENTO CIRCULAR COM GRANDEZAS ANGULARES
t
V
∆s
to
V
φ
φo
φo: ângulo de fase inicial
φ: ângulo de fase final
∆φ: deslocamento angular
∆s
∆φ =
⇒ ∆s = ∆φ ⋅ r
φ=0
↓
o
origem
r
• Velocidade angular média: ωm =
r



 rad



∆φ
(rad/s)
∆t
• ω: velocidade angular instantânea
• Relação fundamental do MCU: V = ω ⋅ r
2. MOVIMENTO CIRCULAR UNIFORME — CINEMÁTICA
•
ωm = CTE ⇒ ω =
∆φ
∆t
• Período (T): intervalo de tempo decorrido em uma volta. Unidade: s.
• Freqüência (f): número de voltas completadas em uma unidade de tempo. Unidade: Hz ou rpm (1Hz = 60 rpm).
• Relações importantes do MCU:
f=
1
T
ω=
2π
T
ω = 2πf
• Equação horária do MCU: φ = φ0 + ωt
3. MOVIMENTO CIRCULAR UNIFORME — DINÂMICA
V
V
ac
ac
o
r
→
→
• V varia em direção, mas não em intensidade (a→T = 0 )
SISTEMA ANGLO DE ENSINO
◆
1◆
2008
Treinamento para Olimpíadas de Física
→
• Aceleração centrípeta (a c) taxa de variação da direção da velocidade.
 • Intensidade: a = V2 = ω2 ⋅ r
c

→
r
→
a

c
•
Direção:
radial
(perpendicular
a V ).

 • Sentido: para o centro da trajetória circular.
• Princípio Fundamental da Dinâmica para o MCU:
→
→
γ→ = a c ⇒ R = m ⋅ a→c
 → R = m ⋅ ac
→

 → R aponta para o centro da trajetória circular.
obs.: Diz-se neste caso, que a resultante é centrípeta. É comum encontrar a expressão força centrípeta. É importante notar que não se trata de um tipo de força (como o peso, tração, etc), pois não corresponde, necessariamente a uma interação entre dois corpos. Força centrípeta significa apenas a componente da resultante que
aponta para o centro da curva.
4. MOVIMENTO CIRCULAR VARIADO (ACELERADO OU RETARDADO) — CINEMÁTICA
∆ω
• Aceleração angular média: αm =
∆t
• α: aceleração angular instantânea.
• Movimento Circular Uniformemente Variado:
α = CONSTANTE = αm ⇒ α =
∆ω
∆t
φ = s/r
φ0 = s0/r
ω0 = V0/r
ω = V/r
α = a/r
αt2

 φ(t): φ = φ0 + ω0 ⋅ t + 2
Equações 
ω(t): ω = ω0 + αt

 Torricelli: ω2 = ω20 + 2 ⋅ a ⋅ ∆φ
5. DINÂMICA DO MOVIMENTO BI-DIMENSIONAL GERAL
→
• V pode variar em intensidade e direção.
→
→
→
→
• a T: taxa de variação da intensidade de V (em movimentos uniformes a T = 0)
→
→
→
→
• a C: taxa de variação da direção de V : (em movimentos retilíneos, a C = 0)
→
→
aT + a
• γ =→
C
M.R.U.
aT = 0
γ=0
Vo
V = Vo
Vo
aT ≠ 0
ac = 0
aT = γ
Vo
V Vo
aT = 0
ac ≠ 0
ac = γ
SISTEMA ANGLO DE ENSINO
aT = γ
V Vo
ac ≠ 0
aT ≠ 0
Vo
γ
ac
γ2 = a2T + a2c
V Vo
◆
2◆
aT
ac
aT
γ
V = Vo
Vo
M.C.R.
aT ≠ 0
Vo
aT ≠ 0
ac = 0
M.C.U.
M.C.U.
ac ≠ 0
M.R.R.
M.R.A.
ac = 0
V Vo
γ2 = a2T + a2c
2008
Treinamento para Olimpíadas de Física
• Princípio Fundamental da Dinâmica:
— Em qualquer movimento:
→
→
R=m⋅γ
 • R = m ⋅ γ→
 → →
 • R e γ têm mesma direção e mesmo sentido.
Em Classe
1.
(OBF-2006) Um ciclista pedala sua bicicleta fazendo com que a engrenagem maior, concêntrica ao eixo do pedal
e tendo um raio RA igual a 10,0 cm, gire com uma freqüência fA igual a 2,0 Hz e transmitia esse movimento à
engrenagem menor por meio de uma corrente. A engrenagem menor, por sua vez, tem raio RB de 4,0cm e é solidária e concêntrica ao eixo da roda traseira, que tem raio R de 30,0 cm. Dadas essas condições, determine:
a) a freqüência de rotação fB da engrenagem menor;
b) a velocidade de translação v da bicicleta.
2.
(OBF-2007) Em um pêndulo cônico temos uma corda de comprimento l e na sua extremidade um corpo de massa m,
que realiza um movimento circular no plano (veja figura). Como conseqüência deste movimento, a corda descreve a figura de um cone, razão pela qual o pêndulo adquire esse nome. Determine:
a) A velocidade angular ω do corpo em função da aceleração da gravidade g, do comprimento l e do ângulo θ de
inclinação da corda.
b) O tempo para o corpo dar uma volta completa no círculo.
θ
l
r
m v
Em Casa
1.
(OBF-2001) Uma partícula realiza um movimento circular uniforme. Sobre tal situação, pode-se afirmar
a) a velocidade da partícula muda constantemente de direção e sua aceleração tem valor constante e não nulo.
b) o movimento é certamente acelerado, sendo a aceleração da partícula paralela à direção da sua velocidade.
c) visto que o movimento é uniforme, a aceleração da partícula é nula.
d) o vetor velocidade aponta para o centro da trajetória circular, sendo perpendicular ao vetor aceleração.
e) o ângulo formado entre os vetores velocidade e aceleração varia ao longo da trajetória.
2.
(OBF-2002) O planeta Terra gira em torno do Sol completando uma volta em 1 ano (3 × 107 s). Supondo que seu
movimento se dê numa órbita circular de raio r = 1,5 × 108 km, com velocidade de módulo constante, a velocidade linear da Terra neste movimento é de
a) 10 m/s.
d) 300 000 km/s.
b) 300 m/s.
e) zero.
c) 30 km/s.
3.
(OBF-2004) Um aeromodelo descreve um movimento circular uniforme com velocidade escalar de 12 m/s,
perfazendo 4 voltas por minuto. A sua aceleração é de
a) 0,0 m/s2
b) 0,8 m/s2
c) 4,8 m/s2
SISTEMA ANGLO DE ENSINO
d) 7,2 m/s2
e) 9,6 m/s2
◆
3◆
2008
Treinamento para Olimpíadas de Física
4.
(OBF-2001) Uma haste fina e retilínea tem uma de suas extremihaste
dades pivotada em um suporte montado sobre uma superfície
horizontal, como ilustrado na figura ao lado. A base encontra-se
suporte
inicialmente em repouso, com o seu comprimento ao longo da
direção vertical. No instante t = 0, a haste tomba em direção à
superfície, atingindo-a após t = 1,5 s
a) Calcule o valor da velocidade angular média da haste durante sua queda até a superfície.
b) Estime o comprimento da haste, sabendo que a sua extremidade livre cai com velocidade escalar média de
π
12
5.
m / s.
(OBF-2001) A equação horária para a posição angular θ (em radianos) em função do tempo t (em segundos) de
uma partícula que executa um movimento circular, de raio igual a 1 m é dada por:
θ(t) = 1 – 2t + t2
No instante t = 1 s calcule
a) o módulo da aceleração centrípeta da partícula;
b) o módulo da aceleração tangencial da partícula.
6.
(OBF-2001) A figura a seguir representa uma partícula de massa m, presa a
um fio ideal e inextensível de comprimento L. O fio faz um ângulo θ constante com a vertical. Durante seu movimento, a partícula descreve uma
circunferência horizontal, num movimento circular e uniforme. O movimento
→
→
g
θ L
ocorre no vácuo. A aceleração da gravidade é g.
Nesta circunstâncias, podemos afirmar que:
a) o corpo está em equilíbrio, já que apresenta força resultante nula.
m
R
b) o corpo não está em equilíbrio, pois para mantê-lo em sua trajetória circular existe uma força dirigida para fora da circunferência.
c) a situação na qual θ é constante e igual a 90° é fisicamente inatingível.
d) se o fio for cortado, o corpo seguirá indefinidamente em movimento retilíneo e uniforme, numa direção tangente
à circunferência.
e) ao montarmos este mesmo dispositivo na Lua, o tempo gasto pelo corpo para dar uma volta completa seria menor
que aquele medido na Terra.
7.
(OBF-2002) Um corpo executa um movimento circular uniforme. Em relação a esta situação, podemos afirmar que
a) como sua velocidade é constante, a força que age sobre ele é nula.
b) a força resultante que atua sobre ele é a força centrípeta.
c) como a força centrípeta cancela a força centrífuga, então a força resultante que atua sobre ele é nula.
d) a força resultante que atua sobre ele é a força centrífuga.
e) a força resultante é sempre igual à força peso.
8.
(OBF-2002) Você já deve ter observado em corridas de circuitos ovais que as curvas são inclinadas. Esta inclinação das curvas, também observadas em rodovias, é para aumentar a segurança e diminuir o risco de derrapagens. Considere que um automóvel realiza uma curva de raio R e ângulo de inclinação θ. Considere também
que a pista está muito escorregadia e o coeficiente de atrito estático entre os pneus do carro e a pista é desprezível,
podendo o carro derrapar ao realizar a curva.
R
θ
a) Represente, num diagrama de forças que atuam no carro durante a curva, identificando-as.
b) Calcule o módulo da velocidade máxima com a qual o carro pode realizar a curva sem risco de derrapar, em função do raio R e do ângulo de inclinação θ.
SISTEMA ANGLO DE ENSINO
◆
4◆
2008
Treinamento para Olimpíadas de Física
9.
(OBF-2000) Um carro de corrida descreve uma trajetória circular, horizontal, de raio 125 m e velocidade de
180 km/h. O veículo derrapa devido à lama e sai da pista, deslocando-se 100 m, em linha reta, até parar. Calcule
a) A razão entre as forças que atuaram no veículo, na trajetória circular (F1) e em linha reta (F2).
b) A velocidade angular do carro na trajetória circular.
10. (OBF-2006) Um trecho de uma montanha russa apresenta uma depressão de raio de curvatura R igual a 8 0 m.
Determine a velocidade que deve ter um vagonete para que, descendo, seus passageiros sofram, no ponto mais
baixo da depressão, uma sensação que seu peso triplicou.
80 m
11. (OBF-2000) Uma esteira movimenta-se entre dois cilindros idênticos de raio 5 cm, numa freqüência de 10 Hz.
Calcule
a) A velocidade que uma pessoa deve ter, sobre a esteira, para “não sair” do local onde se encontra.
b) Colocando um pacote de 20 kg sobre esta esteira e supondo o coeficiente de atrito estático entre ambos de
0,6, qual pode ser a aceleração angular máxima da esteira imprimida para o pacote não derrapar.
12. (OBF-2004) Considere o movimento de um motoqueiro em um globo
da morte, como ilustrado ao lado.
Quando o motoqueiro encontra-se no ponto mais alto da trajetória e a
sua velocidade é a mínima para não cair,
a) seu peso deve ser igual a força normal.
b) seu peso mais a força centrípeta deve ser igual à força normal.
c) a força normal é a força resultante sobre o motoqueiro.
d) a força peso é a força resultante sobre o motoqueiro.
e) a força resultante sobre o motoqueiro é nula.
Globo da morte
13. (OBF-2002) Um cachorro está preso por uma corda num poste quando vê um gato e, obviamente, decide ir atrás
dele. O cachorro, porém, por mais força que faça, não consegue romper a corda, que suporta uma tração de até
1000 N. Sendo ele o cachorro de um cientista, ele sabe que pode tentar romper a corda girando em torno do
poste. Supondo que o tamanho da corda seja 1 m, a massa do cachorro m = 20 kg, e o movimento seja circular
uniforme, determine
a) qual deve ser a velocidade linear mínima que o cachorro deve ter para que consiga romper a corda.
b) quanto tempo o cachorro demora para dar uma volta completa em torno do poste, com esta velocidade. De posse
destes resultados, comente se é possível supor que o cachorro conseguirá arrebentar a corda.
SISTEMA ANGLO DE ENSINO
◆
5◆
2008
Treinamento para Olimpíadas de Física
AULA 7
MOVIMENTOS BALÍSTICOS
• Movimentos realizados perto da superfície da Terra, desprezando-se a resistência do ar.
• A única força que age sobre o corpo é o peso. Logo:
→
→
→
→
→
→
R = P ⇒ mγ = mg ⇒ γ = g
• Portanto, a aceleração é constante, vertical, para baixo, e não depende da massa do corpo.
• São classificados de acordo com a velocidade inicial.

→

→
1. QUEDA LIVRE (V0 = 0 )
• M.U.V. na direção vertical (y).
• Movimento retilíneo acelerado.
• É conveniente colocar a origem no ponto de lançamento e orientar a trajetória para baixo. Assim:
 y0 = 0

 v0 = 0
 a=+g

y0 = 0
v0 = 0
Equações:

g 2
 y(t): y =
t

2

 v(t): v = gt

 Torricelli: v2 = 2gy
y
v
y

→
2. LANÇAMENTO VERTICAL (V0 vertical)
•
•
•
•
M.U.V. na direção vertical (y).
Movimento retilíneo retardado na subida e acelerado na descida.
No ponto mais alto da trajetória, v = 0.
É conveniente colocar a origem no ponto de lançamento e orientar a trajetória no sentido da velocidade inicial.
→
a) V 0 para cima:
 y0 = 0

 v0 = V0
 a = –g

Equações:

g
 y(t): y = V0t –
t2

2

 v(t): v = V0 – gt

2
 Torricelli: v2 = v0 – 2gy
y
v
y
y0 = 0
→
b) V 0 para baixo:
 y0 = 0

 v0 = V0
 a = +g

Equações:

g
 y(t): y = V0t +
t2

2

 v(t): v = V0 + gt

2
 Torricelli: v2 = v0 + 2gy
SISTEMA ANGLO DE ENSINO
v0
y0 = 0
y
y
◆
v
6◆
2008
Treinamento para Olimpíadas de Física

→
3. LANÇAMENTO HORIZONTAL (V0 horizontal)
• M.U. na direção horizontal (x).
• M.U.V (acelerado) na direção vertical (y).
• É conveniente colocar a origem no ponto de lançamento, orientar o eixo x no sentido da velocidade inicial e o eixo y
para baixo.
• Trajetória parabólica:
vx = V0
V0
0
vx = V 0
vx = V 0
vy
vy
trajetória: arco de parábola
v
v x = V0
vy
vy
y
v







x0 = 0; y0 = 0
vx = V0 (CTE)
v0y = 0
ay = + g
• Equações:
Direção x:
{ x(t): x = V0t

g
 y(t): y =
t2

2
Direção y: 
 vy(t): vy = gt

2
 Torricelli: vy = 2gy
→
4. LANÇAMENTO OBLÍQUO (V0 faz um ângulo θ com a horizontal)
• M.U. na direção horizontal (x).
• M.U.V. (retardado na subida e acelerado na descida) na direção vertical (y).
• É conveniente colocar a origem no ponto de lançamento, orientar o eixo x no sentido da velocidade inicial e o eixo y
para cima.
• No ponto mais alto da trajetória, vy = 0, então V = vx = V0cosθ.
• Trajetória parabólica:
y
vx
vy = 0
trajetória: arco de parábola
v
vy
vx
vx
vy







vy
v
v0y = v0 ⋅ senθ
θ
vx
vx
vx
vx
x0 = 0; y0 = 0
vx = V0 cosθ (CTE)
v0y = V0 sen θ
ay = – g
x
vx = v0 ⋅ cosθ
vy
v
SISTEMA ANGLO DE ENSINO
◆
7◆
2008
Treinamento para Olimpíadas de Física
• Equações:
Direção x:
{x(t): x = V0 cos θ ⋅ t

g 2
 y(t): y = V0sen θ ⋅ t –
t

2
Direção y:  v (t): v = V sen θ – gt
 y
y
0

2
 Torricelli: vy = (V0 sen θ)2 – 2gy
Em Classe
Um canhão repousa sobre
uma superfície horizontal, fazendo um ângulo θ com a mesma. Ele atira um projétil
→
com velocidade inicial V 0. Pode-se desprezar a resistência do ar. Sendo g a intensidade do campo gravitacional
→
local, determine, em função de θ, V 0 e g:
a)
b)
c)
d)
e)
f)
g)
h)
i)
O tempo decorrido até o corpo atingir a altura máxima.
A velocidade do corpo neste instante.
A altura máxima.
O tempo decorrido até o corpo retornar à superfície horizontal.
A velocidade do corpo neste instante.
O alcance do projétil.
Para qual valor de θ o alcance é máximo.
A equação da trajetória.
Preencha a tabela abaixo, substituindo V0 = 10 m/s e g = 10 m/s2.
θ
Altura máxima (m)
Alcance (m)
30°
45°
60°
90°
j) Esboce as trajetórias para os 4 casos do item anterior.
y (m)
6
5
4
3
2
1
x (m)
0
1
2
3
4
5
6
7
8
9
10
Em Casa
1.
(OBF-2005) Um corpo é lançado para o alto com uma velocidade igual a 5 m/s. Qual a altura máxima que o corpo
irá alcançar?
2.
(OBF-2006) Um objeto é lançado verticalmente para cima e atinge, no ponto mais alto de sua trajetória, uma altura igual a 20 m. Desconsiderando a resistência do ar, determine:
a) a velocidade com que foi lançado;
b) em quanto tempo, após o lançamento, ele retorna ao ponto de partida.
SISTEMA ANGLO DE ENSINO
◆
8◆
2008
Treinamento para Olimpíadas de Física
3.
(OBF-2002) Quando deixamos uma pedra cair de uma altura de 5 m, próximo à superfície da Terra, ela demora 1s
para atingir o solo. Sabendo-se que a aceleração da gravidade na Lua é seis vezes menor que na Terra, o tempo
que uma pedra demora para atingir o solo lunar, caindo desta mesma altura é
a) 6 vezes menor
b) 6 vezes maior.
c) O mesmo
d) Aproximadamente 2,5 vezes maior.
e) Aproximadamente 2,5 vezes menor.
4.
(OBF-2004) Uma bolinha de aço, abandonada a 1m de altura de um piso muito duro, realiza um movimento periódico de subida e descida, por tempo indeterminado se desconsiderarmos as perdas de energia na resistência do ar
e nas colisões com o solo. De que altura deve-se abandonar, simultaneamente com a primeira, uma segunda bolinha
para que a sua terceira colisão com o solo coincida com a quinta colisão da primeira bolinha?
5.
(OBF-2001) Um estudante no topo de um edifício observa a trajetória de uma bolinha lançada verticalmente para
cima no instante t = 0, a partir de um ponto localizado abaixo do topo. Medindo a posição a partir do topo, ele nota
que a bolinha atinge a altura de 10m quando t = 1s, e 15m quando t = 2s. Despreze o atrito da bolinha com o ar.
a) Calcule o módulo da velocidade inicial da bolinha.
b) Calcule a distância total percorrida desde o início do lançamento até o instante em que a bolinha atinge a altura
máxima.
6.
(OBF-2001) Um motociclista pretende saltar sobre um conjunto de automóveis enfileirados. As rampas de salto e
de descida têm a mesma altura, comprimento 50 m e inclinação de 15° com a horizontal. A frente de cada automóvel de comprimento 5 m está encostada à traseira do automóvel seguinte. Despreze a resistência do ar.
a) Calcule quantos automóveis o motociclista conseguirá saltar se sua velocidade inicial na base da rampa for
30 m/s e sua aceleração constante ao longo da rampa for 1 m/s2.
b) Calcular qual deverá ser a sua aceleração constante ao longo da rampa se, para realizar um salto igual ao anterior,
a sua velocidade inicial na base da rampa for 25 m/s.
7.
(OBF-2004) Dois rapazes brincam de tênis na praia. Um deles dá uma raquetada na bola a 2,45 m de altura,
imprimindo-lhe uma velocidade de 72 km/h na horizontal. Qual deve ser a velocidade mínima do outro rapaz, situado inicialmente a 20,3 m à frente do primeiro, para que consiga aparar a bola antes que ela bata na areia?
8.
(OBF-2000) No instante em que um veículo vai iniciar, a 72 km/h, a travessia de uma ponte de 80 m de altura uma
pessoa do interior do carro lança horizontalmente uma pedra, com velocidade de 5 m/s perpendicular a sua velocidade em direção ao despinhadeiro. A pedra atinge o solo, no instante em que o veículo conclui a travessia. Calcule:
a) Qual o comprimento da ponte.
b) A posição da pedra, em relação ao veículo, quando ele atinge o solo.
9.
(OBF-2007) Uma roda gigante de raio 5,0m tem o seu eixo a 6,6m do solo e se encontra girando, com velocidade
constante, no sentido horário. Quando uma das cadeiras chega à posição que forma 53° com direção vertical (veja
figura), a criança que a ocupa lança uma bola para o alto, na direção vertical, com velocidade de 8,8m/s. Sabendo
que o período do movimento da roda gigante é de 10π s, determine o ponto em que a bola vai atingir o solo.
53°
giro
5m
6,6 m
10. (OBF-2005) Um carrinho, que se move com velocidade constante igual a 2,0m/s, possui um dispositivo com uma
mola, inicialmente comprimida, capaz de lançar verticalmente para cima uma pequena bola. Este dispositivo pode ser
SISTEMA ANGLO DE ENSINO
◆
9◆
2008
Treinamento para Olimpíadas de Física
acionado por um gatilho quando o carrinho passa por um determinado ponto de sua trajetória, deixando a partir daí a
mola distendida. A bolinha é então arremessada verticalmente com velocidade igual a 5m/s (despreze a resistência
do ar).
a) Qual a velocidade da bolinha quando esta alcançar o ponto mais alto de sua trajetória?
b) Esboce o movimento da bolinha e do carrinho, visto por um observador parado no solo, para um tempo de 2
segundos a partir do momento que a bolinha é lançada para o alto.
AULA 8
DINÂMICA IMPULSIVA
1. INTRODUÇÃO
→
→
→
→
• Seja um corpo de massa m que se move com velocidade V . Suponha que neste corpo ajam as forças F 1, F 2, F 3, …
durante um→ certo intervalo de tempo ∆t. O objetivo central da dinâmica consiste em determinar qual será a
velocidade V do corpo após as forças terem agido sobre ele. Para tanto,
1. Determina-se a resultante destas forças:
→
→
→
→
→
R = Σ F = F1 + F2 + F3 + …
→
2. Utiliza-se o Princípio Fundamental da Dinâmica para calcular a aceleração γ causada no corpo por estas forças:
→
→
→
R = mγ
3. Caso →
γ seja constante, é simples determinar V’:
r
r r
r
∆ V V’ − V
=
⇒ V’ = V + ∆t ⋅ γ
γ = CTE ⇒ γ = γm =
∆t
∆t
→
→
→
• Entretanto, caso R não seja constante, γ também não será, de forma que não se pode calcular V ’ assim. Existem
muitas situações em que isso ocorre. Uma delas é a colisão de uma bolinha (de tênis, por exemplo) contra uma
parede. A figura abaixo mostra→instantes sucessivos desta situação desde quando a bolinha se aproxima
da parede
→
(instante t0) com velocidade V até se afastar dela após a colisão (instante t’) com velocidade V ’, passando por
→
instantes intermediários (t1, t2, t3) em que a bola está em contato com a parede, recebendo dela uma força F que
→
→
causa a deformação vista e altura sua velocidade de V para V ’.
V
F
t0
F
t1
F
t2
t3
V’
t’
→
• Observa-se que F não é constante. Sua intensidade varia, de forma qualitativa, segundo o gráfico abaixo, em que
∆tINTERAÇÃO costuma ser bem pequeno:
F
t
t0
t1
t2
t3
t’
∆tINTERAÇÃO
SISTEMA ANGLO DE ENSINO
◆
10 ◆
2008
Treinamento para Olimpíadas de Física
→
• A determinação de V ’ em problemas como este requer a introdução de dois novos conceitos: impulso e quantidade
de movimento.
2. IMPULSO DE UMA FORÇA E QUANTIDADE DE MOVIMENTO
→
• Se uma força F de intensidade constante age em um corpo durante um intervalo de tempo ∆t, define-se o impulso
desta força como:
 Grandeza vetorial
→
→
→

IF = F ⋅ ∆t  Mesma direção e sentido de F

 Unidade: N ⋅ s
→
• Caso F não seja
constante, a única forma de calcular o seu impulso é →
pela área sob um gráfico F × t. Define-se a
→
força média F m como a força que causaria o mesmo impulso que F , agindo no mesmo intervalo de tempo,
conforme mostra a figura abaixo:
F
F
→
IF
→
= Fm
⋅ ∆t
Fm
MESMA
ÁREA
IF
IF
t
t
t0
t’
t0
t’
∆t
∆t
→
• Define-se a quantidade de movimento de um corpo de massa m que se move com velocidade V como:
 Grandeza vetorial
→

Q = mV  Mesma direção e sentido de V

 Unidade: kg ⋅ m/s (= N ⋅ s)
→
→
3. PRINCÍPIO FUNDAMENTAL DA DINÂMICA PARA VALORES MÉDIOS
• Quando a resultante das forças que agem em um campo não for constante, é conveniente aplicar o princípio fundamental da dinâmica para valores médios:
→
→
Rm = mγ m
r
• Como a aceleração vetorial média γ→m é calculada como γm =
→
→
∆ V V’ − V
=
, então:
∆t
∆t
→
Rm ⋅ ∆t = mV’ – mV
• Pode-se escrever a equação acima com as grandezas definidas na seção anterior:
→
→
→
I R = Q’ – Q
• Lê-se: o impulso da resultante das forças que agem em um corpo é igual à variação da quantidade de movimento deste
corpo. A equação acima é também chamada de teorema do impulso.
4. SISTEMA ISOLADOS
• Uma das principais aplicações do teorema do impulso é o estudo de sistemas isolados: conjuntos de corpos em
que a somatória de todas as forças externas é nula. Um exemplo é a colisão entre duas bolas de bilhar A e B se deslocando sobre uma mesa com a qual o atrito é desprezível:
NA
A
vA
B
vB
FB/A
SISTEMA ANGLO DE ENSINO
vA’
FA/B
PA
ANTES
NB
vB ’
PB
DURANTE
DEPOIS
◆
11 ◆
2008
Treinamento para Olimpíadas de Física
• A aplicação do teorema do impulso a cada uma das bolas conduz a:
→
→
→
 RmA ⋅ ∆t = Q’A – QA
→
→
→
 RmB ⋅ ∆t = Q’B – QB
• A quantidade de movimento de um sistema é a soma das quantidades de movimento de todos os corpos que fazem
parte deste sistema (no caso, as bolas A e B). Logo, somando-se as duas equações acima, obtém-se:
→
→
→
→
(RmA + RmB) ⋅ ∆t = Q’SIST – QSIST
• A resultante das forças que agem em um corpo é a soma vetorial de todas
elas.
Algumas destas forças são internas,
→
→
ou seja, aplicadas por corpos do próprio sistema (no caso, as forças F A/B e F B/A, aplicados pela bola A sobre a bola
B e vice-versa,
respectivamente); outras são externas
, ou→seja, aplicados por corpos de fora do sistema (no caso, os
→
→

→
peso P A e P B, aplicados pela Terra, e as normais NA e NB, aplicadas pela mesa). Como a resultante é a soma de
todas as forças aplicadas a um corpo, ela é a soma das forças internas e das forças externas.
A soma das resultantes
→
aplicadas aos corpos do sistema será, portanto, a somatória de todas as forças internas (ΣF INT) com todas as forças
→
externas (ΣF EXT).
Desta forma:
→
→
→
→
(ΣF EXT + ΣF INT) ⋅ ∆t = Q’SIST – QSIST
→
• Pelo
Princípio da Ação-Reação, se um corpo A aplica uma força F em uma corpo B, ele receberá deste uma força
→
– F . Pertencendo ambos os corpos ao sistema, ambas as forças serão internas, e sua soma será nula. Isso ocorrerá
quaisquer que sejam os corpos
A →e B do sistema, e quaisquer que sejam as forças trocadas por ele. Por isso, pode→
se concluir que, sempre, ΣF INT = 0 .
→
→
• Caso as forças externas sejam tais que ΣF EXT = 0 , então a equação anterior implica que a quantidade de movimento
do sistema se conserva. Este é o enunciado do teorema dos sistemas isolados :
→
→
→
→
→
→
0 = Q’SIST – QSIST ⇒ Q’SIST = QSIST
→
• Note que ΣF EXT = 0 significa que a soma de todas as interações de corpos do sistema com corpos de fora do
sistema é zero, ou seja, tudo se passa como se não houvesse nenhuma força externa: como se o sistema
não
→
→
interagisse absolutamente com o restante do universo. Por esta razão, diz-se que um sistema em que ΣF EXT = 0 é
um sistema isolado.
• As duas bolas de bilhar do exemplo apresentado acima formam um sistema isolado, pois:
→
→
→
→
→
→
→
→
ΣF EXT = P A + NA + PB + NB = 0 + 0 = 0 .
123 123
→
→
=0
=0
• Portanto, segundo o teorema dos sistemas isolados, a quantidade de movimento do sistema se conserva:
→
→
→
→
→
→
Q’SIST = QSIST ⇒ mAV’A + mBV’B = mAVA + mBVB
5. COEFICIENTE DE RESTITUIÇÃO
• Toda colisão é, com boa aproximação, um sistema isolado. Entretanto, apenas o teorema dos sistemas isolados não basta
para estudar uma colisão de dois pontos materiais. Uma informação adicional acerca da natureza da colisão é necessária: o coeficiente de restituição da colisão, definido como:
e=
| v’A – v’B |
=
vA – vB
Vafastamento
Vaproximação
• Pode-se mostrar que o coeficiente de restituição se relaciona com a conservação da energia mecânica em uma colisão.
A tabela a seguir classifica as colisões de acordo com os valores do coeficiente de restituição.
Natureza da Colisão
Coef. Restituição
Energia Mecânica
Elástica
e=1
εm’ = εm: Sist. conservativo
Parcialmente Elástica
0e1
εm’ εm: Sist. Não-conservativo
Inelástica
e=0
εm’ εm: Sist. Não-conservativo
SISTEMA ANGLO DE ENSINO
◆
12 ◆
2008
Treinamento para Olimpíadas de Física
• Como se nota, apesar de em toda colisão a quantidade de movimento se conservar, a energia mecânica só se conserva nas colisões elásticas, que são aquelas em que a velocidade de afastamento dos corpos é igual à velocidade
de aproximação.
Em Classe
(OBF-2007) Em uma mesa de bilhar estão dispostas três bolas idênticas de massa m = 200g, em repouso. Um jogador toca a bola 1 com um taco, exercendo sobre ela uma força de módulo F = 5N, paralela à superfície da mesa.
Após 0,2s da aplicação da força, a bola 1 atinge a bola 2. Observa-se que, após o choque, as bolas 1 e 2 passam a
mover-se em direções que formam 60° e 30°, respectivamente, com a direção original da bola 1. Após certo tempo a
bola 2 colide com a bola 3 e fica em repouso, enquanto a bola 3 segue em direção à caçapa, atingindo-a em 0,3s.
Considerando os choques elásticos e desprezando o atrito entre as bolas e a superfície, pergunta-se:
a) A velocidade da bola 3 ao atingir a caçapa;
b) A distância percorrida pela bola 3 até atingir a caçapa.
Em Casa
(OBF-2000) Um objeto de 400 g é solto do repouso de uma altura de 80 m e atinge o solo, nele penetrando.
Sobre o corpo atua uma força constante de 4000 N para detê-lo.
a) Calcule o tempo que a força atuou sobre o objeto.
b) Quanto o objeto penetrou no solo?
2.
(OBF-2001) Uma bolinha de borracha de massa 0,1 kg cai em queda livre, a partir do repouso, de uma altura de
12,8 m. Após a primeira colisão com o solo, cuja duração é 0,2 s, a bolinha sobe verticalmente e atinge uma altura
máxima de 9,8 m. Despreze a resistência do ar.
a) Calcule a quantidade de movimento (momento linear) da bolinha imediatamente antes e depois da colisão (indique claramente o módulo, a direção e o sentido em cada caso). Houve conservação da quantidade de movimento?
Explique sua resposta.
b) Calcule a força média que o solo exerce sobre a bolinha durante a colisão (indique claramente o módulo, a direção e o sentido).
3.
(OBF-2004) Uma bola, de massa igual a 100 g, é abandonada de uma altura de 1,25 m, bate no chão e torna a subir
até a altura de 0,80 m. Desprezando a resistência do ar, determine:
a) o coeficiente de restituição;
b) o impulso do chão sobre a bola;
c) a força máxima exercida pelo chão sobre a bola, considerando que a colisão dure 20m/s e que a variação da força
com o tempo seja como no gráfico abaixo.
F(N)
1.
t(s)
4.
(OBF-2005) Os movimentos, em uma linha reta, de dois corpos A e B são descritos pelo gráfico a seguir, que relaciona as quantidades de movimento com o tempo. Qual a intensidade média da força de interação que o corpo A
exerceu sobre o corpo B?
q (kg ⋅ m/s)
A
80
5
– 20
SISTEMA ANGLO DE ENSINO
10
15
t(s)
B
◆
13 ◆
2008
Treinamento para Olimpíadas de Física
5.
(OBF-2007) Um garoto de massa m está num pequeno barco, de massa M, que se encontra em repouso em um lago
de águas paradas. Em um determinado momento ele anda com velocidade v de um extremo do barco ao outro.
Desprezando os efeitos dissipativos,
a) Qual será a velocidade do barco em relação à margem?
b) Se o barco fosse transformado num navio, qual seria a velocidade do navio?
6.
(OBF-2006) Uma bola de chumbo de massa mB igual a 5 kg é lançada com uma velocidade VB que faz com que ela
caia e fique imobilizada dentro de um carrinho, conforme mostrado no desenho. O carrinho tem massa mc igual a
10 kg e se move com velocidade constante Vc = 5 m/s.
10 m
VB
5m
VC
a)calcule o valor da velocidade VB com que a bola colide com o carrinho;
b) calcule a velocidade V com que o carrinho se movimentará após ter recebido a bola de chumbo.
7.
(OBF-2006) A figura mostra a mão de um jardineiro segurando o bico de uma “mangueira” de regar jardins e o jato
de água da mesma batendo em uma parede e sendo espelhado perpendicularmente ao bico da mangueira. Supondo
o escoamento igual a 1,0kg de água por segundo, a velocidade da água no interior da mangueira VE igual a 0,25 m/s
e a velocidade da água ao sair pelo bico Vs igual a 2,0 m/s, pede-se determinar:
VE
VS
a) o valor da força horizontal que o jardineiro exerce para equilibrar a força associada à mudança de velocidade
da água no bico da “mangueira”.
b) o valor da força de reação exercida pela parede contra o jato de água.
SISTEMA ANGLO DE ENSINO – Coordenação Geral: Nicolau Marmo; Coordenação Pedagógica: Marco Antônio Gabriades; Supervisão
de Convênios: Helena Serebrinic; Equipe 1a e 2a série Ensino Médio: Luis Ricardo ARRUDA de Andrade, DANILO Pereira Pinseta, PEDRO Nery
Lavinas, Maurício DELmont de Andrade; Projeto Gráfico, Arte e Editoração Eletrônica: Gráfica e Editora Anglo Ltda;
SISTEMA ANGLO DE ENSINO
◆
14 ◆
2008
Treinamento para Olimpíadas de Física