A v - Instituto de Física / UFRJ

Módulo 4 – Sistema de Partículas e
Momento Linear
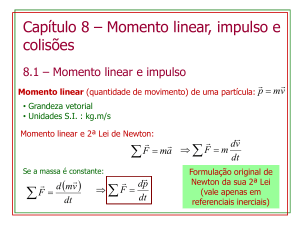
Momento linear


Momento linear (quantidade de movimento) de uma partícula: p  mv
• Grandeza vetorial
• Unidades S.I. : kg.m/s
Momento linear e 2ª Lei de Newton:



dv


F

m
 F  ma 
dt
Se a massa é constante:
 d mv 
 F  dt
 dp
 F 
dt
Formulação original de
Newton da sua 2ª Lei
Conservação do momento linear
Considere um sistema isolado: Ausência de forças externas
Exemplo: Par de astronautas, onde há apenas forças internas

FB sobre A


Par ação-reação: FA sobre B   FB sobre A

FA sobre B


d
p

B
F

 A sobre B
dt
Pela 2ª Lei: 


d
p
F
 A
B
sobre
A

dt






dpB dp A d  p A  pB 
Assim: FA sobre B  FB sobre A 


0
dt
dt
dt
 

Definindo o momento linear total: P  p A  pB

Na ausência de forças externas (sistema isolado),
dP
Temos:
0
ou se a resultante das forças externas for
dt
nula, o momento linear total se conserva
Lei de Conservação do Momento Linear:
• Pode ser facilmente generalizada para um número qualquer de
partículas
•É consequência da 3ª Lei de Newton
Colisões
Antes
m1

m2

Depois

v1

v2
Durante

m1

m2

v1

v2
Interação entre pares de partículas com duração extremamente curta.
Muitas vezes não conhecemos os detalhes da interação, temos acesso
apenas às velocidades logo antes e logo depois da colisão.
Aplicações
Física de partículas elementares
Rutherford (descoberta do núcleo)
Na maioria das colisões, podemos supor um sistema isolado: Forças
internas têm tipicamente duração muito mais curta e intensidade muito
maior que as forças externas – podemos usar a conservação do
momento linear
No entanto, a energia cinética não se conserva necessariamente:
• Colisão elástica: energia se conserva
• Colisão inelástica: energia não se conserva
• Colisão totalmente inelástica: perda de energia cinética é
máxima (partículas ficam grudadas depois da colisão)
Colisões elásticas
ANTES
A
Caso geral em 1D
Conservação do momento linear:
vB
DEPOIS
mAvA  mB vB  mAvA  mB vB
Conservação da energia:
vA
B
vA
A
B
vB
1
1
1
1
mAv A2  mB vB2  mAvA2  mB vB2
2
2
2
2
Conhecendo-se as massas e as velocidades iniciais, podemos obter
as velocidades finais (2 equações e 2 incógnitas)
Caso particular em 1D: uma das
massas inicialmente parada
ANTES
A
Conservação do momento linear:
vA
vB  0
DEPOIS
mAvA  mAvA  mB vB
Conservação da energia:
B
vA
1
1
1
mAv A2  mAvA2  mB vB2
2
2
2
  m A  mB
v A  m  m v A

A
B
Depois de alguma álgebra: 
v  2m A v
 B m A  mB A
A
B
vB
vA  0
Caso ainda mais particular: mA  mB 
vB  v A
Procedimento experimental
Seguindo o guia de laboratório, faremos 2 experimentos: colisão
elástica e colisão totalmente inelástica
I – Colisão Elástica
a. Selecionar 2 carrinhos com massas idênticas
b. Verificar a instalação do centelhador para que ele registre o
movimento de ambos carrinhos
c. Montar uma tabela x(t) para os dois carrinhos
d. Obter, a partir do programa de ajuste linear, as respectivas
velocidades
e. Verificar a conservação do momento linear e da energia cinética
f. Fazer gráfico x(t) para os dois carrinhos na mesma folha de papel
Incertezas
Momento linear de uma partícula:
p  mv
 m   v 
p  p     
 m  v 
2
2
Se pudermos desprezar a incerteza da massa:
Momento linear total de 2 partículas:
P  p A  pB
P 
p A 2  pB 2
pv
p 
v
Energia cinética de uma partícula (como vimos no Módulo 3):
1 2
K  mv
2
 m 
 v 
K  K    4 
 m
 v 
2
2
Se pudermos desprezar a incerteza da massa:
Energia cinética total de duas partículas:
K  K A  KB
K 
K A 2  K B 2
(fim da primeira aula)
K 
2 Kv
v
Centro de massa
Posição do centro de massa de
um sistema de N partículas:
i
2

m
r
 ii
0
N




m r  m2 r2  ...  mN rN
Rcm  1 1

m1  m2  ...  mN

ri
1
i 1
N
m
i
i 1
Média, ponderada pelas massas, das posições das partículas
Em componentes:
X cm
m1 x1  m2 x2  ...  mN xN


m1  m2  ...  mN
N
m x
i 1
N
i i
m
i 1
i
(idem para y e z)
Movimento do centro de massa




m1r1  m2 r2  ...  mN rN
Rcm 
m1  m2  ...  mN
Velocidade do centro de massa:





dRcm m1v1  m2v2  ...  mN vN
Vcm 

dt
m1  m2  ...  mN
Massa total: M  m1  m2  ...  mN





MVcm  m1v1  m2v2  ...  mN vN  P (momento linear total)
Momento linear total é igual à massa total
multiplicada pela velocidade do centro de massa
Como vimos, se a resultante das forças externas for nula, ou se o
sistema for isolado:


P  constante  Vcm  constante
Colisões no referencial do centro de massa:
• ausência de forças externas, velocidade do c.m. permanece
inalterada pela colisão
• referencial do c.m. é inercial

vA
A

vA
A
Trajetória
do c.m.

vB
B
A

u A

uA
A
B
C.m. está
parado

u B

uB
B
Referencial do c.m.

vB
B
Referencial do laboratório
Velocidades no referencial
do centro de massa:




u A  v A  Vcm




u B  vB  Vcm




u A  v A  Vcm




u B  vB  Vcm
Conservação do momento linear:



mA u A  Vcm






mAvA  mB vB  mAvA  mB vB






 mB uB  Vcm  mA u A  Vcm  mB uB  Vcm









mAu A  mBuB  mAu A  mBuB
Momento linear também se conserva no referencial do centro de
massa (como esperado, pois trata-se de um referencial inercial)

Energia cinética no referencial do lab:
Antes:
1
1
2
Ec  mAv A  mB vB2
2
2
Mudança de variáveis para velocidade do c.m. e velocidade relativa:



mAv A  mB vB

Vcm 
mA  mB

v  v  v  u  u (independe do referencia l)
A
B
A
B
 rel
Invertendo, obtemos:

mB

v A  Vcm  m  m

A
B



v  V  m A
cm
 B
m A  mB

vrel

vrel
Substituindo na expressão para a energia cinética:
1
1
2
Ec  mAv A  mB vB2
2
2
2
2
1 
mB   1  
mA  
Ec  mA Vcm 
vrel   mB Vcm 
vrel 
2 
mA  mB
mA  mB
 2 

Após alguma álgebra:
Definindo:
1
1 mA mB 2
2
Ec  mA  mB Vcm 
vrel
2
2 mA  mB
M  mA  mB
mA mB

mA  mB
(massa total) e
(massa reduzida)
Obtemos finalmente:
1
1 2
2
Ec  MVcm  vrel
2
2
Energia cinética do movimento
do centro de massa
Energia cinética do
movimento relativo
Análise:
1. Parece com a expressão da energia cinética de duas “partículas”
2. No referencial do c.m., temos:
cm
c
E
1 2
 vrel
2
( vel. do c.m.  0)
Ou seja, a energia cinética depende do referencial, e a energia
cinética mínima é aquela calculada no referencial do c.m.
3. Antes e depois de uma colisão, a velocidade do c.m. não varia,
de modo que a variação da energia cinética é:
1
1 2
2

Ec  vrel  vrel
2
2
Ou seja, a variação de energia cinética não depende do referencial
(como esperado)
4. Em uma colisão elástica, temos:


1
1 2
2
  vrel  0  vrel  vrel

Ec  vrel
2
2
Ou seja, o módulo da velocidade relativa não é alterado pela colisão
5. A perda máxima de energia cinética (colisão totalmente
inelástica), ocorre quando: 0
1
1 2
1 2
2
  vrel   vrel
Ec  vrel
2
2
2
Desta forma, explica-se porque as partículas ficam “grudadas”
depois de uma colisão totalmente inelástica
Procedimento experimental
II – Colisão Totalmente Inelástica
a. Selecionar 2 carrinhos com massas diferentes: o carrinho
inicialmente em repouso deve ter massa 100g maior que a do
carrinho incidente
b. Verificar a instalação do centelhador para que ele registre o
movimento de ambos carrinhos
c. Montar a seguinte tabela:
t(s)
x1
(cm)
δx1
(cm)
x2
(cm)
δx2
(cm)
XCM (cm)
δXCM (cm)
x'1 (cm)
δx'1 (cm)
x„2 (cm)
δx„2 (cm)
0,0
...
...
...
...
...
...
...
...
...
...
0,1
...
...
...
...
...
...
...
...
...
...
0,2
...
...
...
...
...
...
...
...
...
...
d. Seguindo o guia, calculamos a energia e o momento linear antes e
depois da colisão, em ambos referenciais
e. Fazer gráficos de x1, x2 e XCM em uma folha
f. Fazer gráficos de x‟1 e x‟2 (posições no ref. Do CM) em outra folha
Incertezas
Posição do centro de massa:
X cm
X cm
m1 x1  m2 x2

m1  m2
2
2
m

m
1
2
2
1
2

m12 x1   m22 x2   0,1 cm 
m1  m2
m1  m2
(desprezando as incertezas nas massas)
Posições no referencial do CM:
xi 
xi 2  X cm 2
xi  xi  X cm