Lista_cinematica - Cursinho Popular de Jandira

FÍSICA
LISTA DE MECÂNICA – CINEMÁTICA
Velocidade Média
Conceitos iniciais
Para um corpo que vai de um ponto A para um ponto B,
sendo a trajetória vista de cima a linha azul (torta), temos:
Quanto ao tempo, temos um intervalo de tempo (2hs de
duração por exemplo) ou um instante de tempo (a aula
começa às 13hs30).
No sistema internacional de unidades (SI), tempo e espaço
são medidos em segundos e metros.
(01) Uma corrida de formula 1 teve uma duração 1h 46 min
36 s.
(a) Sabendo que a corrida teve 65 voltas, determine o
intervalo de tempo médio gasto para cumprir cada uma das
voltas.
(b) Se a corrida começou às 14hs, em que instante de tempo
ela terminou?
(02) Amy dá três voltas completas numa pista de corrida
circular de 2m de raio.
(a) Qual foi a distância percorrida por Amy?
(b) Se as voltas foram completas, qual foi a posição final de
Amy em relação à posição inicial?
(c) Qual será a distância final de Amy em relação ao ponto
de partida?
(dica: fórmula do comprimento da circunferência: C=2πR,
onde posso considerar π = 3,14)
(03) Efetue as seguintes conversões de unidades a seguir:
(a) 10 km em m; (b) 2 m em cm; (c) 2 h em s; (d) 2m em
mm. (e) 1 dia em s (f) 1 ano em s
Lembrando que no movimento retilíneo uniforme (onde a
velocidade não varia) a velocidade instantânea é igual à
velocidade média.
(04) Um ônibus leva duas horas para ir de São Paulo a
Porto Feliz. A distância que ele percorre nas estradas em
que passa, no total, dá perto de 200 quilômetros. Qual será
a velocidade média do ônibus neste percurso? (a resposta
pode ser dada em km/h)
(05) Joana está na casa de sua avó e resolve visitar também
sua tia. Sua casa, a casa de sua avó e a casa de sua tia ficam
na mesma rua. De sua casa até a casa de sua avó são 100m
de distância. De sua casa até a casa de sua tia são 310m de
distância. Joana pega a bicicleta e vai da casa da avó para a
casa da tia em 1min40s.
(a) Esquematize as casas na rua segundo suas posições com
as informações contidas no enunciado.
(b) Qual é a distância entre a casa de sua avó e a casa de
sua tia?
(c) Qual foi a velocidade média de Joana na bicicleta?
(06) Uma águia-real voa normalmente a 50km/h, mas
quando mergulha no ar para alcançar uma presa no chão,
chega a 320km/h! Se uma águia está numa altitude de
9000m (a altura estimada do Everest é de 8848m), num
mergulho, quanto tempo ela leva para atingir a presa (que
está no chão)?
(07) Estima-se que uma pessoa consiga correr no máximo a
43km/h. O avião no qual o amor da minha vida vai
embarcar parte daqui a 15min. Segundo o GPS do meu
celular, estou a 5000m do aeroporto. Se eu for correndo até
lá, poderei chegar a tempo de impedir meu amor de
embarcar?
(08) Um carro faz o percurso abaixo esquematizado da
seguinte forma: no início o carro vai a 20m/s até chegar
numa árvore onde fazem uma pausa de 10min para um
piquenique, o restante da viagem é feita a 10m/s a fim de
não deixar os passageiros enjoados.
produzido o relâmpago até onde está o indivíduo. (A
velocidade da luz é aproximadamente 300 000 km/s).
(13) Um atirador aponta para um alvo e dispara um
projétil. Este sai da arma com velocidade de 300 m/s. O
impacto do projétil no alvo é ouvido pelo atirador 3,2 s
após o disparo. Sendo 340 m/s a velocidade de
propagação do som no ar, calcule a distância do atirador
ao alvo.
Unidades e conversão de velocidades
(a) Em quanto tempo a viagem é feita?
(b) Qual foi a velocidade média do percurso?
(09)(FUVEST-SP) Após chover na cidade de São Paulo,
as águas da chuva descerão o rio Tietê até o rio Paraná,
percorrendo cerca de 1000 km. Sendo 4 km/h a
velocidade média das águas, o percurso mencionado será
cumprido pelas águas da chuva em aproximadamente:
(a) 30 dias; (b) 10 dias; (c) 25 dias; (d) 2 dias; (e) 4 dias.
(10)(FUVEST-SP) Diante de uma agência do INPS há
uma fila de aproximadamente 100 m de comprimento, ao
longo da qual se distribuem de maneira uniforme 200
pessoas. Aberta a porta, as pessoas entram, durante 30 s,
com uma velocidade média de 1 m/s.
Avalie:
(a) o número de pessoas que entram na agência;
(b) o comprimento da fila que restou do lado de fora.
(14) Faça as seguintes conversões (neste exercício
não tem problema em se usar calculadora, principalmente
do item f ao m):
(a) 20m/s em km/h
(b) 10m/s em km/h
(c) 5m/s em km/h
(d) 1m/s em km/h
(e) 300m/s em km/h
(f) 20km/h em m/s
(g) 10km/h em m/s
(h) 1km/h em m/s
(i) 300km/h em m/s
(j) 10km/min em m/s
(k) 10km/s em m/s
(l) 10m/min em m/s
(m)10m/h em m/s
(n) 1000m/h em km/h
Velocidade relativa
SENTIDOS IGUAIS - as velocidades se subtraem
SENTIDOS OPOSTOS - as velocidades se somam
(11)(FUVEST-SP) Um ônibus sai de São Paulo às 8 h e
chega a Jaboticabal, que dista 350 km da capital, às 11 h
30 min. No trecho de Jundiaí a Campinas, de
aproximadamente 45 km, a sua velocidade foi constante e
igual a 90 km/h.
(a) Qual a velocidade média, em km/h, no trajeto São
Paulo – Jaboticabal ?
(b) Em quanto tempo o ônibus cumpre o trecho Jundiaí –
Campinas ?
(15) Um bêbado, dirigindo a 80 km/h entra numa
contramão e bate de frente no carro de uma
família que vinha a 40 km/h. Qual é a
velocidade do carro do bêbado em relação
ao carro da família?
(PS. Para que a batida fosse equivalente, se
o carro da família estivesse parado, o carro
do bêbado teria que estar na velocidade da
resposta)
(12) Durante uma tempestade, um indivíduo vê um
relâmpago, mas ouve o trovão 5 s depois. Considerandose o som no ar, com velocidade praticamente constante e
igual a 340 m/s determine:
(a) a distância que separa o indivíduo e o local do
relâmpago;
(b) o tempo que a luz levou para ir do local onde foi
(16) Estou correndo num campo florido com uma
velocidade de 10m/s, quando um passarinho dá um rasante
em minha direção (se aproxima). Eu vejo o passarinho
vindo a 30m/s (velocidade em relação a mim). Qual era a
velocidade real do passarinho?
(17) Fui com minha irmã até a estação de trem. Despedi-me
e entrei no meu vagão. Minha irmã acenou, virou-se e
caminhou em direção a saída. O trem começou a se mover
na direção oposta a ela. A velocidade do trem, inicialmente é
de 1m/s. A velocidade do caminhar de minha irmã é de
0,5m/s. A que velocidade eu a vejo se afastar de mim,
quando estou dentro do trem?
(18) Minha sobrinha tem 3 anos e gosta de brincar de piqueesconde. Ela consegue correr numa velocidade de no
máximo 0,5m/s, enquanto durante a brincadeira, eu corro a
1m/s. Se ela está correndo de mim e eu a alcançar, com que
velocidade ela vê eu me aproximar dela?
(19) Um tubarão persegue um peixe com uma velocidade de
20m/s para a direita. O peixe foge do tubarão com uma
velocidade de 20m/s. Um pato, na superfície, tenta alcançar
o peixe, mas a velocidade máxima do pato é de 10m/s.
Ainda nessa mesma situação, uma água viva nada
tranquilamente a 2m/s para a esquerda. E um siri, parado no
fundo do rio assiste a tudo. A situação segue esquematizada
abaixo. Calcule:
torcedores assistem a um jogo. Através de cada uma das
6 saídas disponíveis podem passar 1000 pessoas por
minuto. Qual o tempo mínimo necessário para se
esvaziar o estádio ?
(a) uma hora; (b) meia hora; (c) 1/4 de hora;
(d) 1/3 de hora; (e) 3/4 de hora.
Velocidade relativa com velocidade média
(22) Dois cavalos correm numa estrada, um em direção ao
outro, com velocidades 1m/s e 3m/s até que se chocam.
Inicialmente estão a uma distância de 100m um do outro.
Enquanto isso uma mosca voa com velocidade constante de
10m/s do focinho de um cavalo ao focinho do outro, indo e
voltando, até que os cavalos se chocam esmagando a
mosca.
(a) Quanto tempo os cavalos levam para se chocar?
(b) Que distância a mosca percorre antes de morrer?
(a) Qual é a velocidade do siri em relação a todos os
outros animais.
(b) Qual é a velocidade do tubarão em relação a
todos os outros.
(c) Qual é a velocidade do peixe em relação a todos
os outros.
(d) Qual é a velocidade da água-viva em relação a todos os
outros.
(e) Qual é a velocidade do pato em relação a todos
os outros.
(f) O pato ou o tubarão vão comer o peixe?
(20) Durante o dia, vemos o Sol se mover no céu, mas
sabemos que na verdade é a Terra que se move em torno do
Sol. Se a terra tem uma velocidade de 30 km/s em torno do
Sol, considerando que a trajetória dela em torno do Sol seja
aproximadamente circular, qual é a distância entre o Sol e a
Terra?
(dica / lembrando: comprimento da circunferência
= 2πR; π=3,14; um dia tem 24hs, um ano 365 dias)
(21)(FUVEST-SP) No estádio do Morumbi 120000
(FUVEST-SP) Uma composição ferroviária (19 vagões e
uma locomotiva) desloca-se a 20 m/s.
Sendo o comprimento de cada elemento da composição
10 m, qual é o tempo que o trem gasta para
ultrapassar:
(a) um sinaleiro ? (b) uma ponte de 100 m de
comprimento ?
(23) Dois trens A e B correm em trilhos paralelos no
mesmo sentido. Num determinado momento, A ultrapassa
B. A velocidade de A é de 10m/s, a velocidade de B é de
5m/s e os dois trens têm 100m de comprimento. Quanto
tempo vai demorar a ultrapassagem completa dos trens?
Classificação de movimentos
Os movimentos que estudaremos a seguir serão:
M.R.U. - movimento retilíneo uniforme
M.R.U.V. - movimento retilíneo uniformemente variado.
Quanto à variação do espaço eles podem ser:
(24) Classifique o movimento do elevador nas seguintes
situações (considere o espaço orientado para cima) como
MRU ou MRUV, progressivo ou retrógrado e acelerado ou
retardado (caso seja MRUV):
(a) começando a subir (acelerado).
(b) subindo (velocidade constante)
(c) parando na subida (desacelerado)
(d) começando a descer (acelerado)
(e) descendo (velocidade constante)
(f) parando na descida (desacelerado)
(25) As tabelas abaixo fornecem as velocidades de duas
bicicletas em função do tempo:
Quanto à variação da velocidade ele podem ser:
Em cada caso, classifique o movimento em progressivo
ou retrógrado, acelerado ou retardado.
Movimento retilíneo uniforme (M.R.U.)
Equação horária
A equação horária de um movimento é a que dá a posição
em função de um instante de tempo. Ou seja, se eu quiser
saber a posição do corpo num determinado instante, é só
substituir o valor do instante na equação horária e poderei
encontrar o valor da posição. São exemplos de equações
horárias:
S = 25 + t ; S = t2 + 7 ; S = 42t + 7 .
A equação horária do M.R.U. é:
S = S0 + v t
S (em metros) = posição no instante t
S0 (em metros) = posição inicial
v (em metros/segundo) = velocidade
t (em segundos) = instante de tempo
(conhecida como fórmula do sorvete)
OBS. Lembrando que o sinal da velocidade indica se o
movimento é progressivo (velocidade positiva) ou
retrógrado (velocidade negativa).
(2) Gráfico de velocidade x tempo : no MRU a
velocidade é constante, e igual em todos os
instantes.
(26) Um móvel descreve um movimento retilíneo
uniforme, de acordo com a função horária:
s = −20 + 5t (SI)
Para esse móvel determine:
(a) o espaço inicial e sua velocidade escalar;
(b) a posição no instante t = 10s;
(c) o instante em que ele passará pela origem dos espaços.
(27) Um trem de 100m de comprimento, a uma
velocidade constante de 10 m/s demora 1 min para
atravessar uma ponte. Determine o comprimento da
ponte.
(28) Dois carros, A e B, se deslocam numa pista retilínea,
ambos no mesmo sentido e com velocidades constantes.
O carro que está na frente desenvolve 72 km/h e o que
está atrás desenvolve 126 km/h. Num certo instante, a
distância entre eles é de 225 m.
(a) Quanto tempo o carro A gasta para alcançar o carro
B?
(b) Que distância o carro que está atrás precisa percorrer
para alcançar o que está na frente ?
(3) Gráfico de posição x tempo : obedece a equação
horária que corresponde à equação da reta.
(29) Duas estações A e B estão separadas por 200 km,
medidos ao longo da trajetória. Pela estação A passa um
trem P, no sentido de A para B, e simultaneamente passa
por B um trem Q, no sentido de B para A. Os trens P e Q
têm movimentos retilíneos e uniformes com velocidades
de valores absolutos 70 km/h e 30 km/h, respectivamente.
Determine o instante e a posição do encontro.
M.R.U. - Gráficos
(1) Gráfico de aceleração x tempo : no MRU a
velocidade é constante, a aceleração é nula em todos
os instantes.
Lembrando que a equação da reta é:
y= b+ax
a = coeficiente angular
b = coeficiente linear
y= b+ax
S = S0 + v t
Determine:
(a) a função horária do movimento;
(b) a posição do móvel no instante t = 30 s;
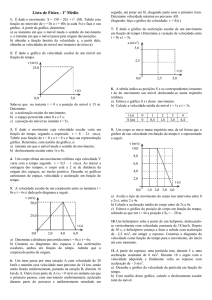
(31) O diagrama horário representa o comportamento da
velocidade escalar de um móvel em função do tempo.
No instante t = 0, o móvel encontra-se na posição so = 3
m.
(a) Determine o deslocamento do corpo nos primeiros 10
s.
(b) Escreva a função horária para o espaço escalar.
(c) Determine o espaço do corpo após 10 s do início do
movimento.
(d) Construa um esboço do gráfico s x t deste
movimento.
E, nos gráficos de velocidade por tempo, a área sob o
gráfico é numericamente igual ao espaço percorrido.
QUANDO EU TENHO UM GRÁFICO, A PRIMEIRA
COISA QUE EU FAÇO É OLHAR AS OORDENADAS!
O GRÁFICO É DE QUE PELO O QUE?
(30) Um móvel se desloca segundo o diagrama da figura.
(32)(Mackenzie-SP) Uma partícula está em movimento
retilíneo e suas posições variam com o tempo de acordo
com o gráfico ao lado.
No instante t = 1,0 minuto, sua posição será:
(a) 5,0 m; (d) 300 m;
(b) 12 m; (e) 1.200 m.
(c) 20 m;
(33)(PUC-RJ) O gráfico relaciona a posição (s) de um
móvel em função do tempo (t).
A partir do gráfico pode-se concluir corretamente que:
(a) o móvel inverte o sentido do movimento no instante t
= 5 s;
(b) a velocidade é nula no instante t = 5 s;
(c) o deslocamento é nulo no intervalo de 0 a 5 s;
(d) a velocidade é constante e vale 2 m/s;
(e) a velocidade vale – 2 m/s no intervalo de 0 a 5 s e 2
m/s no intervalo de 5 a 10 s.
Movimento Uniformemente variado
M.R.U.V. - aceleração média
A aceleração escalar média é a variação de
velocidade no percurso (final menos inicial) pelo tempo
gasto no percurso (instante final menos inicial).
No MRUV a aceleração média do percurso é igual à
aceleração instantânea, porque neste tipo de movimento a
aceleração é constante.
(34) Um automóvel parte do repouso e atinge a
velocidade de 108 km/h após um tempo de 5 s.
Calcule a aceleração escalar média do automóvel, nesse
intervalo de tempo, em m/s2.
(35)(VUNESP-SP) Um automóvel de competição é
acelerado de forma tal que sua velocidade (v) em função
do tempo (t) é dado pela tabela abaixo. A aceleração
média em m/s2 no intervalo de 5 a 15 s é:
(a) 4,5; (b) 4,33; (c) 5,0; (d) 4,73; (e) 4,0.
M.R.U.V.
Equação de variação de velocidades (vovô ateu)
v = v0 + a t
Equação horária.
S = S0 + v0 t + a t2/2
Equação de Torricelli
v2 = v02 + 2 a ΔS
(36) Um móvel realiza um MRUV e sua velocidade varia
com o tempo de acordo com a função:
v = −20 + 4t (SI)
Determine:
(a) a velocidade inicial e a aceleração escalar;
(b) sua velocidade no instante t = 4 s;
(c) o instante em que atingirá a velocidade de 20 m/s;
(d) o instante em que ocorrerá a inversão no sentido do
movimento.
(37) Um ponto material parte do repouso com aceleração
constante e 4 s depois tem velocidade de
108 km/h. Determine sua velocidade 10 s após a partida.
(38) Um móvel realiza um MRUV regido pela função
horária:
s = 3 + 2t − t 2 (SI)
Determine:
(a) o espaço inicial, a velocidade inicial e a aceleração;
(b) a função velocidade;
(c) o espaço e a velocidade do móvel no instante 2 s;
(d) o instante em que o móvel inverte o sentido do
movimento;
(e) o instante em que o móvel passa pela origem dos
espaços.
(39)(FUVEST-SP) Um veículo parte do repouso em
movimento retilíneo e acelera a 2 m/s2. Pode-se dizer
que sua velocidade e a distância percorrida, após 3
segundos, valem, respectivamente:
(a) 6 m/s e 9 m; (b) 6 m/s e 18 m; (c) 3 m/s e 12 m;
(d)12m/s e 36m; (e) 2 m/s e 12 m.
(40) Um móvel em MRUV parte do repouso e atinge a
velocidade de 20 m/s. Se a aceleração do móvel é 2 m/s2,
determine a distância percorrida por esse móvel.
(41) Um carro em alta velocidade (120 km/h) observa o
semáforo indicar vermelho. Ao mesmo tempo uma
pessoa atravessa sobre a faixa de segurança. Sabendo
que a distância entre o carro e faixa de segurança é de 50
m, pergunta-se qual deve ser a aceleração mínima para
que o carro pare a tempo de evitar uma catástrofe.
M.R.U.V. – Gráficos
(b) Qual a função horária da velocidade ?
(c) Qual a velocidade do corpo no instante 20 s ?
(43) A posição inicial para o móvel que descreve o
movimento retilíneo, cujo gráfico v x t é o representado
ao lado, vale 5 m.
Quais são as equações horárias para o movimento
considerado ?
(44) Um móvel descreve um movimento em que sua
velocidade escalar varia com o tempo de acordo com o
gráfico ao lado.
Propriedades
(42) O gráfico ao lado fornece a velocidade de um corpo
no decorrer do tempo.
Calcule:
(a) a aceleração escalar desse móvel no instante t = 3 s;
(b) seu deslocamento entre os instantes t = 2 s e t = 12 s.
(45)(FUVEST-SP) Um trem de metrô parte de uma
estação com aceleração uniforme até atingir, após 10 s, a
velocidade 90 km/h, que é mantida durante 30 s, para
então desacelerar uniformemente durante 10 s até parar
na estação seguinte.
(a) Represente graficamente a velocidade em função do
tempo.
(b) Calcule a distância entre as duas estações.
(c) Calcule a velocidade média do trem nesse percurso.
(46) É dado o gráfico da velocidade em função do tempo
para um móvel que realiza um movimento em trajetória
retilínea.
(a) Qual a aceleração do corpo ?
Classifique o movimento (MRU ou MRUV, progressivo
ou retrógrado, acelerado ou retardado) para cada um dos
trechos da curva dada.
(47) Um ponto material movimenta-se segundo:
s = 12 – 4t (SI)
Faça os gráficos das funções: s = f(t), v = f(t) e a = f(t)
desse movimento.
(48) O espaço de um ponto material varia no decurso de
tempo de acordo com o gráfico. Determine:
(50) Uma pedra é lançada do solo, verticalmente para
cima, com velocidade de 18 m/s. Desprezando a
resistência do ar e adotando g = 10 m/s2, determine:
(a) as funções horárias do movimento;
(b) o tempo de subida;
(c) a altura máxima;
(d) em t = 3s, contados a partir do lançamento, o espaço
doa pedra e o sentido do movimento;
(e) o instante e a velocidade escalar quando o móvel
atinge o solo.
(51) Um corpo é lançado verticalmente para cima, com
velocidade de 20 m/s, de um ponto situado a 160 m do
solo. Despreze a resistência do ar e adote g = 10 m/s2.
(a) Qual o tempo gasto pelo corpo para atingir o solo ?
(b) Qual a velocidade do corpo no instante 5 s ?
(a) o espaço inicial do movimento;
(b) o que acontece com o ponto material no intervalo de
tempo de 2 s a 5 s;
(c) em que instantes o móvel passa pela origem;
(d) a velocidade escalar no instante 1,5 s.
(49)(FEI-SP) O gráfico da aceleração escalar de um
móvel, em movimento retilíneo, em função do tempo é
dado na figura. Determine:
(52) Uma pedra é abandonada do topo de um prédio e
gasta exatamente 4 segundos para atingir o solo.
Despreze a resistência do ar e adote g = 10 m/s2.
Determine:
(a) a altura do prédio;
(b) o módulo da velocidade da pedra ao atingir o solo.
(53)(UNICAMP-SP) Uma torneira, situada a uma altura
de 1 m acima do solo, pinga lentamente à razão de 3
gotas por minuto.
(a) Com que velocidade uma gota atinge o solo ?
(b) Que intervalo de tempo separa as batidas de duas
gotas consecutivas no solo ? Considere, para simplificar,
g = 10 m/s2.
(54) Uma bola de tênis é arremessada verticalmente para
cima, partindo do chão, com uma velocidade de 20 m/s.
Em que instantes a bola estará a 15 m acima do chão ?
(a) a aceleração escalar média no intervalo de 0 a 40 s;
(b) o gráfico da velocidade escalar em função do tempo.
Sabe-se que a velocidade inicial é nula.
MRUV - Queda livre
É um MRUV na vertical com aceleração igual à aceleração
da gravidade, ou g. A equação horária, por exemplo, fica:
S = S0 + v0 t + g t2/2,
onde S e S0 são as alturas final e inicial.
(55) Dois móveis A e B são lançados verticalmente para
cima, com a mesma velocidade inicial de 15 m/s, do
mesmo ponto. O móvel A é lançado no instante t = 0 e o
móvel B é lançado 2 s depois.
Determine, a contar do ponto de lançamento, a posição e
o instante do encontro dos móveis. Adote
g = 10 m/s2 e despreze a resistência do ar.
(56)(UNICAMP-SP) Um malabarista de circo deseja Ter
3 bolas no ar em todos os instantes. Ele arremessa uma
bola a cada 0,40 s. (Considere g = 10 m/s2.)
(a) Quanto tempo cada bola fica no ar ?
(b) Com que velocidade inicial deve o malabarista atirar
cada bola para cima ?
(c) A que altura se elevará cada bola acima de suas
mãos ?
MRUV - Lançamento oblíquo
(60) Procure jogar um jogo chamado “Angry Birds”. Deve
ter na internet, no facebook, procurem!
M.C.U. - Movimento circular uniforme
Período: tempo que demora para ocorrer um evento.
Frequência: número de eventos que acontece em uma
unidade de tempo.
A fim de estudá-lo, dividimos este tipo de movimento em
dois:
(1) o vertical, que é um MRUV similar à queda livre, e
(2) o horizontal, que é um MRU.
(57) Um projétil é lançado por um canhão num ângulo de 30
graus com o horizonte com uma velocidade de 100 m/s.
(a) Calcule o tempo que o projétil leva para atingir o solo
(dica: use a componente verticais apenas)
(b) Calcule a distância entre o ponto em que a bala atinge o
solo e o canhão. (dica: use a componente horizontal apenas)
(c) Para diminuir a distancia do item (b), o que eu preciso
fazer com o ângulo de lançamento?
(58) Refaça os itens a e b do exercício anterior considerando
que o canhão foi colocado sobre um bloco, estando agora
elevado 5 m do solo.
(59) Um trem anda sobre trilhos horizontais retilíneos
com velocidade constante igual a 80 km/h.
No instante em que o trem passa por uma estação, cai um
objeto, inicialmente preso ao teto do trem.
Pergunta-se:
(a) Qual a trajetória do objeto, vista por um passageiro
parado dentro do trem ?
(b) Qual a trajetória do objeto, vista por um observador
parado na estação ?
(suponha que o trem vai em sentido da estação)
Exemplo: o período de uma estação do ano é de 3 meses
(um quarto de ano), a frequência de estações do ano é 4 por
ano, ou 4 (ano)-1
velocidade angular média: o tanto de ângulo (em radianos)
que ele vai rodar por unidade de tempo (radiano por
segundo, normalmente).
Assim, se eu pegar 360 graus (uma rotação completa) e
dividir pelo período (tempo de uma rotação completa) terei:
ou
Há dois tipos de aceleração possíveis: a aceleração
tangencial (que é a que conhecemos nos demais
movimentos) e a aceleração centrípeta (a aceleração
direcionada para o centro, responsável por o movimento ser
circular).
Exemplo: quando o carro faz uma curva, você pode ou não
estar acelerado (aceleração tangencial) mas você sempre
vai ser arremessado sobre a porta, a força que a porta do
carro faz pra você não sair voando na curva é a responsável
pela aceleração centrípeta.
NEM TODO MOVIMENTO CIRCULAR É
ACELERADO, MAS ODO MOVIMENTO CIRCULAR
TEM ACELERAÇÃO CENTRÍPETA.
(a) Em quanto tempo o automóvel percorre um arco de
circunferência de 30 ?
(b) Qual a aceleração centrípeta do automóvel ?
o
Polias Ligadas
(61) Determine, em unidades do SI, o período e a
frequência nos casos abaixo:
(a) ponteiro dos segundos de um relógio;
(b) ponteiro dos minutos de um relógio;
(c) ponteiro das horas de um relógio;
(d) movimento de rotação da Terra;
(e) movimento de Translação da Terra;
(62) Em 72 s um móvel cuja velocidade escalar é 20 km/h
descreve uma trajetória circular de raio 100 m. Determine
o ângulo descrito pelo móvel nesse intervalo.
(63) (Desafio) Uma partícula executa um movimento
circular de raio R com velocidade escalar v e velocidade
angular ω. Uma outra partícula consegue fazer o mesmo
movimento circular com velocidade escalar 2v. Nestas
condições, qual será a velocidade angular da 2a partícula
em função da 1a.
(64) Um ponto material em MCU efetua 120 rpm. O raio
da trajetória é de 20 cm. Determine:
(a) a frequência, em Hz;
(b) o período, em s;
(c) a velocidade angular;
(d) a velocidade escalar, em m/s;
(e) a aceleração centrípeta, em m/s2.
(65) O planeta Mercúrio efetua uma volta em torno do
Sol em 88 dias (isto é, um ano em Mercúrio é igual a 88
dias terrestres). Determine seu período em segundos e sua
frequência.
(66) O raio da Terra é de 6400 km. Calcule a velocidade
linear de um ponto do equador que se desloca devido à
rotação da Terra.
Dê a resposta em km/h e considere π = 3.
(67) A órbita da Terra em torno do Sol pode ser
considerada aproximadamente circular e de raio
1,5 . 10 km. Determine, nessas condições, a velocidade
linear da Terra em torno do Sol.
Dê a resposta em km/s, considere 1 ano aproximadamente
3,1 . 10 s e faça π = 3,1.
8
7
(68)(FUVEST-SP) Um automóvel percorre uma pista
circular de 1 km de raio, com velocidade de 36 km/h.
(69) Dois cilindros, 1 e 2, giram ligados por uma correia
que não desliza sobre eles, conforme a figura. Os valores
dos raios são: R1 = 20 cm e R2 = 60 cm. Sendo a
frequência de rotação do cilindro 1 igual a 15 rpm, qual
é:
(a) a frequência do cilindro 2 ?
(b) a velocidade linear da correia em m/s ?
(c) a velocidade angular da polia 1 ?
(d) a velocidade angular da polia 2 ?