ESCOLA DE APLICAÇÃO DR. ALFREDO JOSÉ BALBI
UNITAU
APOSTILA
FUNÇÃO EXPONENCIAL
PROF. CARLINHOS
NOME DO ALUNO:
Nº
TURMA:
blog.portalpositivo.com.br/capitcar
1
Antes de iniciarmos o estudo da função exponencial faremos uma revisão sobre potenciação.
1. Potência com expoente natural
Dado um número real a e um número natural n diferente de zero, chama-se potência de base a e expoente
n o número an que é igual ao produto de n fatores iguais a a.
an = a . a . a... a, onde:
a = base
n = expoente
Exemplos:
44 = 4 . 4 . 4 . 4 = 256
(-4)3 = (-4) . (-4) . (-4) = -64
Observação: Para n = 1, temos: a1 = a
Exemplo:
61 = 6
Propriedades
Dados a e b reais e m e n naturais, as seguintes propriedades são válidas:
a) am. an = am +n
para a diferente de zero e m > n)
b)
c) (ab)m = ambm
d)
e) (
(para b diferente de zero)
)n = amn
Observação: para expoentes iguais a zero, convencionou-se que a a0 = 1, com a diferente de zero.
2. Potência com expoente inteiro negativo
com a diferente de zero.
Exemplos:
a)
b)
blog.portalpositivo.com.br/capitcar
2
3. Potência com expoente racional fracionário
com a real positivo e n = 2, 3, 4, ...
Exemplos:
b)
a)
=
=
Equações exponenciais
Uma equação é chamada exponencial quando a incógnita aparece no expoente.
Para resolver uma equação exponencial, você deve reduzir ambos os membros da igualdade a uma mesma
base. Então, basta igualar os expoentes para recair numa equação comum. Há equações exponenciais em
que não é possível reduzir de imediato os dois membros à mesma base, então, para resolvê-las, devemos
recorrer as propriedades da potenciação para reduzir ambos os membros da igualdade a uma mesma base.
Veremos a seguir os três tipos de equações exponenciais, cuja resolução é feita através das propriedades
da potenciação.
1º tipo: São as equações exponenciais onde se igualam potencias de mesma base.
Exemplo: Resolva as equações
a) 5x = 125.
Solução: 5x = 125
5x = 53
x=3
S={3}
b) 9x = 1
Solução: 9x = 1
9x = 90
x=0
S={0}
x
81
3
c) =
256
4
x
x
x
4
81
34
3
3
3 3
Solução : =
⇒ = 4 ⇒ = ; então x = 4
256
4
4
4
4 4
S ={ 4}
d ) 3 x = 4 27
3
4
Solução : 3 = 27 ⇒ 3 = 3 ⇒ 3 = 3 ; logo x =
x
4
x
4
3
x
3
4
3
S=
4
2º tipo : São as equações exponenciais que recaem em equações do 2º grau.
Exemplo: Resolva a equação 32x - 4.3x + 3 = 0.
Solução:
A expressão dada pode ser escrita na forma:
blog.portalpositivo.com.br/capitcar
3
(3x)2 - 4.3x + 3 = 0
Fazendo 3x = y, temos:
y2 – 4y + 3 = 0 resolvendo esta equação temos:
y’ = 1 ou y’’ = 3
Como 3x= y, então:
3 x= 1
3x = 30
x = 0 ou 3x = 31
x=1
S = {0,1}.
3º tipo : São as equações exponenciais onde figuram soma ou subtração no expoente.
Exemplo: Resolva a equação 2x + 1 + 2x – 2 = 9
Solução:
A expressão dada pode ser escrita na forma:
Fazendo 2x = y, temos:
Como 2x = y, então:
2x = 4
2x = 22
x=2 S={2}
EXERCÍCIOS DE FIXAÇÃO DA APRENDIZAGEM
1) Resolva a equações:
a) 25x = 125 Resp: S = {3/2}
x
1
1
=
32 Resp: S={5}
c) 2
1
e) 4
b) 9x = 243 Resp: S = { 5/2}
3
d) 5
2x
27
=
125 Resp: S={3/2}
4x
= 0,25
Resp: S ={1/4}
1
g) 103x = 10000 Resp: S={-4/3}
3
f) 4x= 32 Resp: S={5/6}
h) 10.3x-3=810 Resp: S={7}
i) 2x-4 + 2x = 34 Resp: S={5}
j) 3x + 3x-1– 3x-2 =11 Resp: S={2}
k) 4x-9.2x+8=0 Resp: S={0;3}
l) 32x-2.3x-3=0 Resp: S={1}
blog.portalpositivo.com.br/capitcar
4
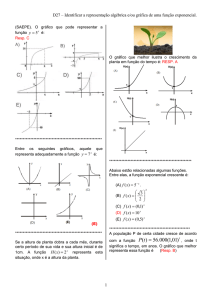
FUNÇÃO EXPONENCIAL
Chamamos de funções exponenciais aquelas nas quais temos a variável aparecendo em expoente.
Dado um número real a (a > 0 e a 1) denomina-se função exponencial de base a, toda função f:IR IR+ definida por
f(x) = ax. O domínio dessa função é o conjunto IR (reais) e o contradomínio é IR+ (reais positivos, maiores que zero).
Exemplos: a) f(x) = 4x
b) y =
Gráfico da função exponencial
O gráfico da função exponencial é uma curva, na qual devemos considerar dois casos:
função crescente
função decrescente
Acompanhe os exemplos seguintes:
1) Construa o gráfico da função:
a) y =2x (nesse caso, a=2, logo a>1)
Atribuindo alguns valores a x e calculando os correspondentes valores de y, obtemos a tabela e o gráfico abaixo:
x
-2
-1
0
1
2
y
1/4
1/2
1
2
4
blog.portalpositivo.com.br/capitcar
5
b) y = (1/2)x (nesse caso, a=1/2, logo 0<a<1)
Atribuindo alguns valores a x e calculando os correspondentes valores de y, obtemos a tabela e o gráfico abaixo:
x
-2
-1
0
1
2
y
4
2
1
1/2
1/4
Nos dois exemplos, podemos observar que
a) o gráfico nunca intercepta o eixo horizontal; a função não tem raízes;
b) o gráfico corta o eixo vertical no ponto (0,1);
c) os valores de y são sempre positivos (potência de base positiva é positiva), portanto o conjunto imagem é
Im=IR+.
2) Uma pessoa deposita R$ 500,00 na caderneta de poupança e, mensalmente, são creditados juros de 2% sobre o
saldo. Sabendo que montante = capital + rendimento, determine:
a) O montante dessa aplicação após x meses.
Resolução: A aplicação na caderneta de poupança está relacionada ao montante do juros compostos, ou seja , M(t) =
C.(1 + i)t, onde:
C( capital) i(taxa de juros em decimal) t(período da aplicação)
No caso, então: M(x) = 500.(1 + 0,02)x
M(x) = 500.(1,02)x
b) O montante, após 1 ano
Resolução: x = 1 ano = 12 meses M(12) = 500. 1,0212 M(12) = 634,12 reais
c) O rendimento no primeiro ano
Sabemos que, montante = capital + rendimento, logo, rendimento = montante – capital, então: rendimento =
634,12 – 500,00 = 134,12 reais
blog.portalpositivo.com.br/capitcar
6
EXERCÍCIOS DE FIXAÇÃO DA APRENDIZAGEM
1) Construa o gráfico, determine o conjunto imagem e classifique em crescente ou decrescente as
funções:
1
b) f(x) = 4
a) f(x) = 4x
Resp: Crescente
Im= R*+
x
1
d) f(x) = 2
c) y = 2x + 1
Resp: Decrescente
Im=R*+
y
Resp: Crescente
Im=[1;∞[
y
x +1
Resp: Decrescente
Im=R*+
y
y
2
1
0
1
x
0
1
x
0
½
x
0
x
2) Chama-se montante (M) a quantia que uma pessoa deve receber após aplicar um capital C, a juros
compostos, a taxa i durante um tempo t. O montante pode ser calculado pela fórmula
M = C(1 + i)t. Supondo que o capital aplicado é de R$ 200.000,00 a uma taxa de 12% ao ano
durante 3 anos, qual o montante no final da aplicação ? Use: 12% = 0,12 Resp: R$ 280.985,60
2 x + 3y = 11
x y
2 - 3 = 5 resp: x = 3 e y = 1
3) Resolva o sitema
4) (Ueg) A bula de certo medicamento informa que, a cada seis horas após sua ingestão, metade dele é absorvida
pelo organismo. Se uma pessoa tomar 200 mg desse medicamento, quanto ainda restará a ser absorvido pelo
t
1 6
organismo imediatamente após 18 horas de sua ingestão? E após t horas? Resp: 25 mg e f(t) = 200.
2
Inequações exponenciais
É toda desigualdade onde a variável figura no expoente. Na resolução da inequação exponencial, devemos
considerar 2 casos
1.º caso – Se a > 1, o sentido da desigualdade é conservada.
blog.portalpositivo.com.br/capitcar
7
2.º caso – Se 0 < a < 1, o sentido da desigualdade se inverte.
Exemplos
01. Resolva a inequação 3x < 9.
Solução:
A inequação proposta pode ser escrita na forma:
3x<32
Observe que as bases são iguais e maiores que 1, então devemos manter o sinal da desigualdade, isto é:
x<2
O conjunto solução da inequação é:
S = {x
x < 2}
02. Resolva a inequação
.
A inequação dada pode ser escrita assim:
.
Observe que a base da inequação é a mesma e menor que 1. Sendo assim, invertemos o sinal da
desigualdade para os expoentes:
4x > 20
x > 5.
Então, S = { x
x > 5}
blog.portalpositivo.com.br/capitcar
8
EXERCÍCIOS DE FIXAÇÃO DA APRENDIZAGEM
1) Resolva as inequações:
a) 4x-1>2x+1 Resp: S = {x∈ℜ/ x >2}
b) (0,1)5x-1≤ (0,1)2x+8 Resp: S = {x∈ℜ/ x ≥3}
1
c) 2
x2 − x
>
1
64 Resp: S = {x∈ℜ/ -2 <x < 3}
Bibliografia:
Curso de Matemática – Volume Único
Autores: Bianchini&Paccola – Ed. Moderna
Matemática Fundamental - Volume Único
Autores: Giovanni/Bonjorno&Givanni Jr. – Ed. FTD
Contexto&Aplicações – Volume Único
Autor: Luiz Roberto Dante – Ed. Ática
blog.portalpositivo.com.br/capitcar
9