Cálculo do Tempo de Sobrecarga em Transformadores

1
Cálculo do Tempo de Sobrecarga em
Transformadores Através do Equivalente
Térmico Simplificado
G. M. F. Ferraz, G. P. Lopes, M. L. B. Martinez
Resumo--Através do conhecimento das variações de carga dos
transformadores de distribuição calculou-se o tempo - até que
sejam atingidas as condições nominais de temperatura – sob
operação em potência superior à nominal, partindo de várias
condições iniciais de operação em potência. Para este cálculo
levou-se em consideração o circuito térmico simplificado obtido a
partir de resultados de ensaios de aquecimento em ambiente
fechado. Os resultados são indicativos, uma vez que nestes casos
não se conhece, de forma exata, os parâmetros construtivos dos
transformadores. Os dados obtidos provem de modelos
simplificados e medições em uma série de ensaios de elevação de
temperatura do topo de óleo. Com os parâmetros fixados
determinou-se a matriz de tempo para os diferentes
carregamentos possíveis, comparando com a metodologia de
cálculo do ponto mais quente em transformadores imersos em
óleo exposta pelo IEEE. Apontando uma alternativa para
determinação do tempo de sobrecarga.
superior a potência nominal são prejudiciais a vida útil dos
equipamentos caso permaneçam por qualquer intervalo de
tempo após se ter atingido temperaturas ligeiramente
superiores a nominal de operação, reduzindo vida útil dos
materiais empregados na sua construção.
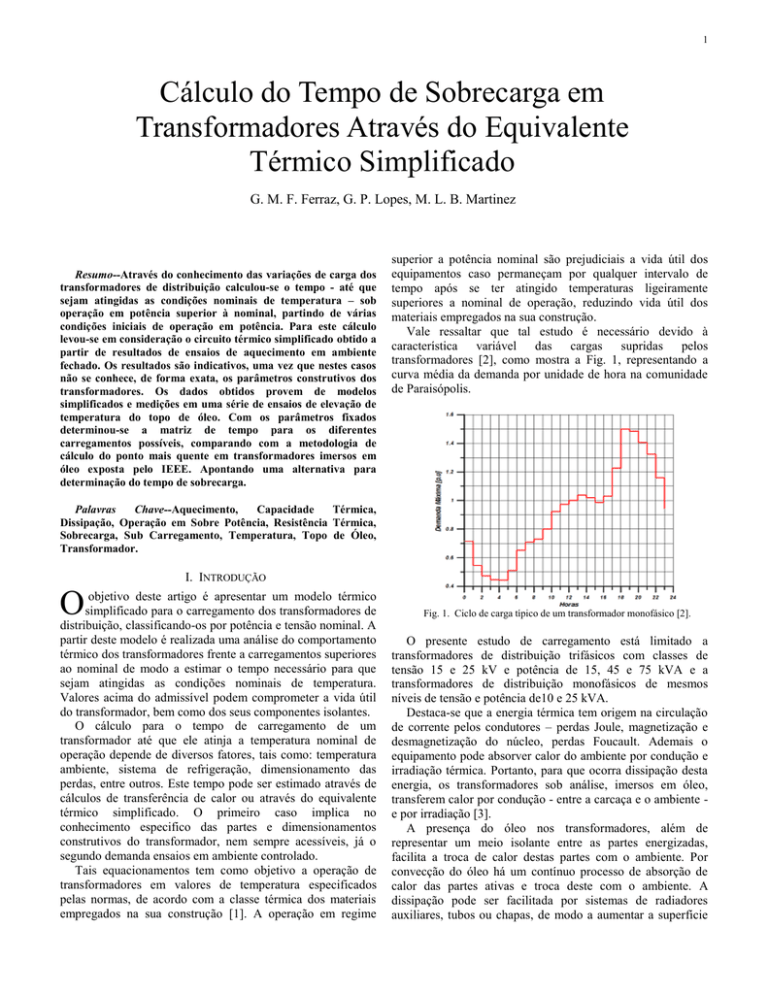
Vale ressaltar que tal estudo é necessário devido à
característica variável das cargas supridas pelos
transformadores [2], como mostra a Fig. 1, representando a
curva média da demanda por unidade de hora na comunidade
de Paraisópolis.
Palavras
Chave--Aquecimento,
Capacidade
Térmica,
Dissipação, Operação em Sobre Potência, Resistência Térmica,
Sobrecarga, Sub Carregamento, Temperatura, Topo de Óleo,
Transformador.
I. INTRODUÇÃO
O
objetivo deste artigo é apresentar um modelo térmico
simplificado para o carregamento dos transformadores de
distribuição, classificando-os por potência e tensão nominal. A
partir deste modelo é realizada uma análise do comportamento
térmico dos transformadores frente a carregamentos superiores
ao nominal de modo a estimar o tempo necessário para que
sejam atingidas as condições nominais de temperatura.
Valores acima do admissível podem comprometer a vida útil
do transformador, bem como dos seus componentes isolantes.
O cálculo para o tempo de carregamento de um
transformador até que ele atinja a temperatura nominal de
operação depende de diversos fatores, tais como: temperatura
ambiente, sistema de refrigeração, dimensionamento das
perdas, entre outros. Este tempo pode ser estimado através de
cálculos de transferência de calor ou através do equivalente
térmico simplificado. O primeiro caso implica no
conhecimento especifico das partes e dimensionamentos
construtivos do transformador, nem sempre acessíveis, já o
segundo demanda ensaios em ambiente controlado.
Tais equacionamentos tem como objetivo a operação de
transformadores em valores de temperatura especificados
pelas normas, de acordo com a classe térmica dos materiais
empregados na sua construção [1]. A operação em regime
Fig. 1. Ciclo de carga típico de um transformador monofásico [2].
O presente estudo de carregamento está limitado a
transformadores de distribuição trifásicos com classes de
tensão 15 e 25 kV e potência de 15, 45 e 75 kVA e a
transformadores de distribuição monofásicos de mesmos
níveis de tensão e potência de10 e 25 kVA.
Destaca-se que a energia térmica tem origem na circulação
de corrente pelos condutores – perdas Joule, magnetização e
desmagnetização do núcleo, perdas Foucault. Ademais o
equipamento pode absorver calor do ambiente por condução e
irradiação térmica. Portanto, para que ocorra dissipação desta
energia, os transformadores sob análise, imersos em óleo,
transferem calor por condução - entre a carcaça e o ambiente e por irradiação [3].
A presença do óleo nos transformadores, além de
representar um meio isolante entre as partes energizadas,
facilita a troca de calor destas partes com o ambiente. Por
convecção do óleo há um contínuo processo de absorção de
calor das partes ativas e troca deste com o ambiente. A
dissipação pode ser facilitada por sistemas de radiadores
auxiliares, tubos ou chapas, de modo a aumentar a superfície
2
de contato.
As perdas dividem-se em perdas a vazio e em carga, que
são representadas em (1).
(
)
(1)
Onde:
– Constante para condução;
– Constante para irradiação;
A – Área total da superfície dos radiadores;
Ar – Área equivalente de radiação;
– Elevação média de temperatura.
transformador em análise, a prática do IEEE relata as
dificuldades na determinação dos parâmetros. Dada as
influências do vento, impedância característica, viscosidade do
óleo, tipo de radiador instalado e variação da temperatura
ambiente. Deste modo, o método assume a influência do
vento, destacado na Fig. 3, como constante. Além disso, aplica
carregamentos constantes considerando que as perdas também
se mantenham fixas. Logo em (2) determina a temperatura de
topo de óleo frente a um carregamento qualquer.
(2)
Onde:
A dissipação de calor em transformadores tem
correspondência com as trocas por dissipação e irradiação, que
influenciam o comportamento frente à aplicação de potências
acima das nominais [4]. Desta forma, a temperatura nominal
de operação tende, em condições controladas e reproduzíveis,
ser diferente para equipamentos com trocadores de calor
distintos. Assim, estes fatores são de extrema relevância em
um estudo dinâmico (com influências ambientais
consideráveis), mas para fins de simplificação e ensaios
laboratoriais foram desprezados.
Destaca-se que a temperatura de operação do transformador
é estimada através da leitura do valor de temperatura no topo
do óleo. As partes ativas, enrolamentos e núcleo, trocam calor
diretamente com o óleo e por convecção, as partículas mais
quentes tendem ao topo do tanque. Ao ceder calor ao ambiente
estas partículas esfriam e descem.
Para a determinação da temperatura de operação e ensaio
utilizou-se a referência normativa ABNT NBR 5356-2, que
estipula os limites de elevação de temperatura, como
apresentado na Tabela I [5]. Para o caso estudado –
transformadores imersos em óleo, sem conservador, sem gás
inerte sob pressão, com circulação natural de óleo– a norma
estabelece 55° C como limite máximo para elevação de
temperatura do transformador.
TABELA I – LIMITES DE ELEVAÇÃO DE TEMPERATURA
– Última temperatura de topo de óleo frente a um
carregamento;
– Variação da temperatura de topo de óleo frente à
variação de temperatura ambiente;
K – Relação da carga frente à taxa de carregamento;
R – Relação entre a perda sob carga pela perda a vazio;
n – É um expoente para perdas totais versus o aumento da
temperatura do topo de óleo.
Equação (3) estipula o transitório de temperatura do topo
de óleo frente ao tempo e um carregamento fixo.
(
) (
)
Onde:
– Temperatura de topo de óleo acima da ambiente;
– Temperatura inicial do topo de óleo antes do ciclo
de carregamento;
l – Carregamento;
t – Tempo em minutos;
– Constante de tempo para temperatura de topo de óleo
frente a diferentes tipos de carregamento.
Por sua vez, tem-se em (4) a determinação da temperatura
do ponto mais quente.
(4)
Limites de elevação de temperatura (°C)
Dos enrolamentos
Sistema de
preservação de
óleo
Sem conservador
e sem gás inerte
sob pressão
Média, por medição da variação
de resistência
Circulação do
Circulação
óleo natural ou
forçada de óleo
forçada sem
com fluxo
fluxo de óleo
dirigido
dirigido
Do ponto
mais
quente
(3)
Do
topo de
óleo
55
60
65
50
95
100
120
60
II. FUNDAMENTAÇÃO TEÓRICA
A. Prática Recomendada IEEE Para Ensaio de Elevação de
Temperatura em Transformadores Imersos em Óleo com
Carregamento Além da Classificação de Potência
O método descrito pela norma IEEE C 57.91 [6] tem foco
na determinação do ponto mais quente do transformador e na
temperatura de topo de óleo. Utilizando diferentes
carregamentos e conhecendo as características construtivas do
Onde:
– Temperatura do ponto mais quente;
– Temperatura ambiente;
– Diferença de temperatura do ponto mais quente do
vento e do topo de óleo;
Por fim, (5) estipula a constante de tempo para temperatura
do topo do óleo sob carga nominal.
(5)
Onde:
– Capacidade térmica;
– Perda total em carga;
Através da utilização de (2) a (5) e conhecendo-se as
características do transformador como: potência nominal,
classe de tensão, tipo trifásico e monofásico, impedância
percentual, perdas a vazio, perdas em carga, temperatura
ambiente e simulando um degrau de potência – de 0.3 p.u.
para 1.2 p.u. – pode-se estimar a variação de temperatura no
3
topo de óleo e nos enrolamentos do transformador, conforme
mostra a Fig. 2, onde se observa que a constante de tempo do
ponto mais quente do transformador e do topo de óleo são
próximas.
Reh e Rhao – obtém-se o circuito equivalente reduzido
mostrado na Fig. 4 e descrito em (6).
Rth
Máx
Cth
W
A
Fig. 4. Circuito Térmico Equivalente Reduzido
Onde:
Cth – Capacidade térmica equivalente;
Rth – Resistência térmica equivalente;
W – Fontes de calor;
– Temperatura ambiente.
Fig. 2. Variação de temperatura entre o ambiente e as partes construtivas do
transformador segundo preceitos do IEEE.
B. Método do Circuito Térmico Equivalente Simplificado
Para fins de análise utilizou-se o circuito térmico
equivalente [7] apresentado na Fig. 3.
( )
(
)
A Fig. 5 mostra o circuito transitório equivalente para o
modelo da Fig. 4.
Rth
Máx
1
sCth
Rhaf
W
s
A
s
A
s
Te
We
Ce
Reh
Ch
Th
Fig. 5. Circuito Térmico Transitório Equivalente Reduzido.
Rhao
Ws
(6)
Ta
Equacionando o comportamento transitório do circuito temse (7).
(
Fig. 3. Circuito Térmico Equivalente.
Onde:
Ce – Capacidade térmica do equipamento em análise;
Ch – Capacidade térmica do ambiente adjacente;
Reh – Resistência térmica do equipamento;
Rhao – Resistência térmica do ambiente adjacente ao
armazenamento;
Rhaf – Resistência térmica variável, representando o calor
perdido pela ação do vento;
Te – Temperatura do equipamento;
Th – Temperatura do local de armazenamento;
Ta – Temperatura ambiente;
We – Potência elétrica dissipada;
Ws – Calor inserido da radiação solar.
Ressalta-se que o circuito térmico apresentado acima é
generalizado para diferentes máquinas ou sistemas elétricos.
Sendo assim, lança-se mão deste para o cálculo em
transformadores.
Simplificando o modelo para um sistema sem a presença
vento – Rhaf igual a zero – ou influência da radiação solar e
calculando as capacidades e resistências térmicas equivalentes
– assumindo que Cth é a soma de Ce e Ch; e Rth a soma de
)
(7)
Onde:
s – Variável de carregamento do transformador.
A manipulação de (7) para explicitar a temperatura
máxima, resulta em (8) e (9).
(
)
(
(8)
)
( )
(9)
Deste modo, tem-se que o comportamento térmico do
transformador frente à aplicação de carga corresponde a um
sistema de primeira ordem [8]. Assumindo a forma
exponencial apresentada em (10).
( )
(
⁄
)
(10)
Onde:
– Diferença máxima de temperatura entre o
transformador e o ambiente;
– Constante de tempo, dependente das características do
transformador.
4
Sabendo que a temperatura de operação do transformador
pode ser determinada pelo circuito apresentado na Fig. 6.
Reduz-se a expressão (11) como a correspondente.
R
SWcc
Wo+S²Wcc
A
Fig. 6. Circuito Térmico Equivalente Reduzido para a Elevação de
Temperatura
(
)
(11)
Assim:
(
)
(12)
Substituindo em (10):
( )
(
⁄
)(
)
(13)
Isolando a variável tempo ( ):
[
( )
(
]
)
(14)
Desta forma pode-se determinar o tempo em que o
transformador opera sob carregamento superior ao nominal
[9]. Por exemplo: dada uma condição inicial, 0,5 p.u. de
carregamento, aplica-se um carregamento de 1.5 p.u.,
observando o comportamento da temperatura do equipamento
até atingir seu valor nominal.
III. PROCEDIMENTO EXPERIMENTAL
A. Determinação dos Parâmetros do Circuito Equivalente
A partir de dados do ensaio de tipo, elevação de
temperatura de transformadores, foi possível determinar o
comportamento térmico frente ao carregamento com potência
nominal. Os transformadores foram divididos, como
mencionado, em grupos segundo os critérios abaixo:
 Tipo Monofásico ou Trifásico;
 Classe de tensão;
 Potência.
As características predominantes para a determinação dos
parâmetros do circuito térmico equivalente dependem
principalmente das características dos materiais e dos dados
acima. Estes fatores também influenciam na manufatura dos
transformadores: isolação e bitola dos condutores,
dimensionamento do núcleo e sistema para dissipação de
calor.
O procedimento para o ensaio de elevação de temperatura
foi conduzido com base na metodologia clássica descrita nas
normas ABNT NBR 5356-2 [5] e IEC 60279 [10]. O
transformador foi alocado em ambiente controlado de modo a
reduzir ao mínimo as variações de temperatura, além da
presença de pelo menos 3 sensores térmicos dispostos entre 1
e 2 metros para o monitoramento da temperatura ambiente.
Durante a realização do ensaio, o transformador não é
submetido a tensões e correntes nominais simultaneamente.
As perdas sob carga à temperatura de referência e as perdas
em vazio devem ser determinadas previamente para que se
aplique a tensão necessária para simular as perdas nominais. O
ensaio tem objetivo duplo: estabelecer a elevação de
temperatura do topo do óleo em regime permanente com
dissipação das perdas totais e estabelecer a elevação de
temperatura média dos enrolamentos sob corrente nominal
com elevação de temperatura do topo do óleo.
®
Através do sistema de monitoramento MONITEK e do
®
software ELEVA realizou-se o ensaio de elevação de
temperatura de topo do óleo [11]. Inicialmente, é energizado o
relé do variador de tensão motorizado, responsável pela
aplicação crescente de tensão até que a potência ativa lida no
software seja igual à soma das perdas totais calculadas. Caso a
potência ativa consumida pelo transformador for maior que a
desejada, é comandada a energização de outro relé que reduz
tensão aplicada sobre o transformador. Este processo garante
que o valor das perdas totais fique constante durante todo o
ensaio. Simultaneamente são registradas as temperaturas é
calculada a elevação de temperatura do topo de óleo. O
sistema descrito acima fica em operação, armazenando os
dados, até que o equilíbrio térmico seja atingido. Isto ocorre
quando a variação acumulada do gradiente de temperatura do
topo de óleo for inferior a 1 [°C] nas últimas três horas.
De posse de uma série de medições capturados durante o
ensaio é gerada uma representação gráfica e através do
software TC-CURVE FIT são estimados os valores
denominados a, b e c que condizem com os das expressões
(15) e (17), visualizados na Fig. 8.
Igualando tem-se:
| |
| |
(15)
Como,
(16)
E
e
são obtidos seguindo o método [8, 9]. Logo
com (12) e (13) determina-se
; ademais:
(17)
Desta forma é possível determinar o valor de
.
De posse de todos estes valores calcula-se primeiramente a
temperatura de operação do transformador sob uma condição
de carga inferior à nominal através de (12). A posteriori, é
aplicado um valor de carregamento superior ao nominal e
extraídos valores de Ts, conforme expressão (14). Para
simular diferentes degraus de potência aplicou-se um
carregamento inicial, variável entre 0,1 até 0.9 p.u., seguido de
um carregamento superior ao nominal variando entre 1,1 a 2,0
p.u.. Deste modo, foram obtidos 90 valores para os tempos de
elevação de temperatura até seus valores nominais.
IV. RESULTADOS E DISCUSSÃO
A. Estudo de Dados
A Tabela II apresenta a classificação dos transformadores.
5
TABELA II – CLASSIFICAÇÃO DOS TRANSFORMADORES
TRIFÁSICO
MONOFÁSICO
GRUPO 3
25 KV
30 KVA
GRUPO 4 GRUPO 5 GRUPO 6 GRUPO 7
25 KV 25 KV 75 15 KV
25 KV
45 KVA
KVA
10 KVA 25 KVA
A Fig. 7 mostra a forma dos resultados obtidos pelo
monitoramento da elevação de temperatura do topo do óleo
®
através do software ELEVA , para o transformador N° 00022
pertencente ao Grupo 5. Com base nos valores obtidos
utilizou-se a diferença de temperatura entre o ambiente e o
topo de óleo no Software TC-CURVE FIT® para determinar o
modelo matemático mais próximo dos resultados do ensaio. O
software permite o levantamento e determinação das margens
de erro visualizado na Fig. 8. Como apresentado no Item II.B,
o melhor modelo matemático para os ensaios de elevação de
temperatura é o exponencial, a partir do qual são obtidas as
constantes para o modelo, analogamente a Equação (14).
A partir dos resultados de uma série de ensaios de
aquecimento em diferentes transformadores de mesma classe
de tensão e potência, elaborou-se a Fig. 9. A variação da
temperatura de acomodação ocorre basicamente pela
característica construtiva do sistema de troca de calor. Dado
que não foi observado correlação entre a resistência percentual
e o gradiente máximo de temperatura, Fig. 10. Em seguida
estabeleceu-se uma média para os valores da constante de
tempo, da resistência e da capacidade térmicas equivalentes,
bem como os erros proporcionais, apresentadas na Tabela III.
Através de (12), obteve-se a temperatura de operação do
transformador frente à aplicação de carregamentos inferiores
aos nominais para os grupos de transformadores apresentados
na Tabela IV.
Fig. 7. Ensaio de Elevação de Temperatura para o transformador 00022.
Fig. 8. Resultados dos Ensaios de Elevação de Temperatura e margem de
incerteza para o transformador 00022.
Por fim, montou-se uma matriz com os valores de tempo
sob carregamentos superiores ao nominal até que sejam
atingidas as condições nominais de temperatura, visualizada
na Fig. 11.
Fig. 9. Variação de temperatura absoluta do Grupo 5.
TABELA III – RESISTÊNCIA E CAPACITÂNCIA TÉRMICA EQUIVALENTES
MÉDIAS
GRUPOS
ΔT (°C)
P0 (W)
PCC (W)
RHE
CE
(K/W)
(W.S/K)
1
52,90
164,0
623,0
0,06722
2703,42
2
43,83
332,0
1027,0
0,03222
3493,00
3
47,18
181,0
534,5
0,06594
2083,43
4
41,33
211,3
714,0
0,04462
2941,77
5
45,62
349,6
1107,3
0,03138
3718,72
6
39,95
52,2
176,2
0,17584
984,84
7
40,89
110,5
373,0
0,08458
1660,77
TABELA IV – GRADIENTE DE TEMPERATURA SOB CONDIÇÕES DE
CARREGAMENTO INFERIOR AO NOMINAL
POTÊNCIA
GRUPOS - TEMPERATURA (°C)
APLICADA
1
2
3
4
5
6
7
EM P.U.
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
TEMPERATURA
(°C)
GRUPO 1 GRUPO 2
15 KV
15 KV
45 KVA 75 KVA
11,44
12,70
14,79
17,72
21,49
26,10
31,54
37,83
44,95
11,03
12,02
13,67
15,99
18,97
22,61
26,91
31,87
37,50
12,29
13,34
15,11
17,57
20,75
24,62
29,20
34,49
40,48
9,75
10,70
12,29
14,52
17,39
20,90
25,04
29,82
35,23
11,32
12,36
14,10
16,53
19,66
23,48
28,00
33,21
39,12
9,49
10,42
11,97
14,14
16,92
20,33
24,36
29,01
34,27
9,66
10,61
12,19
14,39
17,23
20,70
24,80
29,54
34,90
60,0
40,0
20,0
0,0
1,72
1,73
1,75
1,83
1,85
1,85
RESISTÊNCIA PORCENTUAL (Ω)
Fig. 10. Resistência porcentual versus gradiente máximo de temperatura.
De forma análoga determinou-se as constantes de tempo
para os outros grupos de transformadores. Com tempo
máximo variando entre 121 a 202 minutos – situação de carga
inicial 0,1 p.u. e carregamento de 1,1 p.u., e tempo mínimo
entre 8 a 5 minutos – situação de carga inicial 0,9 p.u. e
carregamento de 2,0 p.u. O estudo de propagação de erros
adota incerteza de 2 °C na determinação da temperatura de
operação para carregamentos inferiores ao nominal e de
aproximadamente 4 minutos para o carregamento superior ao
nominal. Fig. 12 mostra a imagem térmica relacionada com
variação do gradiente de temperatura para o transformador
00022. Observa-se que a região mais quente está no topo da
unidade – Topo do óleo. Todavia, nas partes ativas,
enrolamentos e núcleo, a temperatura pode atingir valores
superiores aos aferidos na metodologia de ensaio empregada.
6
métodos para o cálculo das constantes de tempo térmicas
como: cálculo de transferência de calor ou sensores de fibra
optica implicariam, no primeiro caso, de conhecimento a finco
do equipamento e no segundo de uma metodologia intrusiva e
cara, comparado ao preço médio de um transformador de
distribuição. Finalmente, os valores expostos, em uma
situação não ideal, podem aprensentar margens de incertezas
maiores do que as calculadas.
VI. REFERÊNCIAS
[1]
Fig. 11. Tempo médio até a sobrecarga de transformadores dos Grupos 1 e 5.
Fig. 12. Gradiente de Temperatura do Transformador 00022 em regime
nominal de operação.
V. CONCLUSÃO
Variações de carga são comuns aos transformadores de
distribuição, principalmente em regiões residenciais, dado que
o comportamento de consumo é assimétrico entre os que
utilizam a rede. A fim de preservar a integridade do
equipamento, calculou-se o tempo em que o transformador
pode atuar em sobre potência até atingir a temperatura
nominal. Os valores previstos de tempo até sobrecarga levam
em consideração apenas a temperatura do topo de óleo, obtida
a partir do ensaio de elevação de temperatura. Como
observado, esta constante de tempo tende àquela obtida no
cálculo proposto pelo IEEE. Todavia, em uma situação crítica
de carregamento superior ao nominal os valores de
temperatura dos enrolamentos podem apresentar um degrau de
temperatura e atingir valores acima do admitido, considerando
a classe de temperatura dos materiais isolantes de forma mais
rápida do que a do topo de óleo.
Ademais, inúmeras fontes de erro, como a característica da
manufatura dos transformadores que é artesanal, tipos de
trocadores de calor, efeitos do ambiente externo, carregamento
submetido, entre outros, podem contribuir para uma incerteza
no cálculo do tempo até sobrecarga. Todavia, estes aspectos
são pouco significativos frente ponto principal de análise:
Degrau de potência aplicado ao transformador e seu efeito na
temperatura.
Por fim a metodologia proposta para aquisição de dados é
concisa, simples e aplicável ao ensaio elevação de temperatura
de topo de óleo de transformadores. Os dados averiguados nas
tabelas e a propagação de erro não divergiram. Outros
P. S. Georgilakis, Spotlight on Modern Transformer Design ,Springer
2009, p. 33 -43.
[2] A.F.Picanço, "Desenvolvimento de uma metodologia para a aplicação de
transformadores eficientes com base nos perfis de carregamento"
Dissertação de Doutorado, Programa de Pós- Graduação em Engenharia
Elétrica, Universidade Federal de Itajubá, 2009.
[3] W. Reis, Transformadores Fundamentos para Projeto e Cálculo,
EDIPUCRS, 2007, p. 245 – 290.
[4] A. Martignoni, Transformadores, Globo, p. 227 -237.
[5] Norma Brasileira, Transformadores de Potência, ABNT NBR, 5356-2,
Jan 2008.
[6] IEEE C 57.91 – 1995 IEEE Guide for Loading Mineral-Oil-Immersed
Transformers, IEEE Power Engineering Society, S.A. 1957.
[7] O. Hydro, Application Guide for Surge Arresters on Distribution
Systems, Canadian Electrical Association, 1988, p. 44-45.
[8] R. G. Jordão, Transformadores, Edgard Blücher, 2002, p. 84 -87.
[9] A. D´Ajuz, F. M. Resende, F. M. S. Carvalho, I. G. Nunes, J. A. Filho,
L. E. N. Dias, M. P. Pereira, O. K. Filho, S. A. Morais, Equipamentos
Elétricos especificação e aplicação em subestações de alta tensa, Furnas
Centrais Hidroelétricas, 1987, p. 157-159.
[10] IEC/TR 60279 Ed. 1.0 b:1969, Measurement of the winding resistance
of an a.c. machine during operation at alternative voltage.
[11] J.M.E. Vicente, - “Uma contribuição à automação de ensaios em
transformador de distribuição de média tensão”, Dissertação de
Doutorado, Programa de Pós- Graduação em Engenharia Elétrica,
Universidade Federal de Itajubá, 2006.
VII. BIOGRAFIAS
Guilherme Martinez Figueiredo Ferraz nasceu em Mococa, SP, Brasil em
20 de maio de 1989. Em 2009 ingressou se em Engenharia Elétrica com
ênfase em sistemas elétricos de potência pela Universidade Federal de Itajubá
(UNIFEI). No mesmo ano iniciou atividades como colaborador no
Laboratório de Alta Tensão (LAT-EFEI) na mesma universidade. No LATEFEI atua em projetos de P&D em parceria com a AES Sul Distribuidora
Gaúcha de Energia e a Universidade de Bologna e com o Grupo ENERGISA.
Gustavo Paiva Lopes nasceu em Varginha, MG, Brasil em 20 de Maio de
1984. Graduou-se em Engenharia Elétrica com ênfase em sistemas elétricos
de potência pela Universidade Federal de Itajubá (UNIFEI) em 2008. Atuou
na área de consultoria em projetos e estudos elétricos pela empresa TSE –
Tecnologia em Sistemas Elétricos entre 2009 e 2011. Iniciou o mestrado em
Engenharia Elétrica como aluno regular pela UNIFEI em 2011, quando
passou a atuar como colaborador mestrando do Laboratório de Alta Tensão
(LAT-EFEI) na mesma universidade. No LAT-EFEI desenvolve o projeto de
“Coordenação de Isolamentos em Redes de Média Tensão com Neutros
Ressonantes” em parceria com a AES Sul Distribuidora Gaúcha de Energia e
a Universidade de Bologna, Itália.
Manuel Luis Barreira Martinez possui graduação em Engenharia Elétrica
pela Universidade Federal de Itajubá (1982), mestrado em Engenharia Elétrica
pela Universidade Federal de Itajubá (1993), doutorado em Engenharia
Elétrica pela Universidade de São Paulo (2000). Aperfeiçoamento em
Pequenas Centrais Hidroelétricas, Sistemas Elétricos de Potência,
Equipamentos de Manobra, Descargas Atmosféricas em Linhas e Subestações,
Pára raios de Resistor Não Linear para Sistemas de Potência, Técnicas de Alta
Tensão entre outros. Possui experiência no projeto e construção de
equipamentos, componentes e sistemas de ensaios em Alta tensão. Atualmente
é Professor Adjunto da Universidade Federal de Itajubá e Coordenador do
Laboratório de Alta Tensão. É autor e co-autor de ao redor de 250 artigos
divididos entre seminários nacionais, internacionais e periódicos.
7