ETE_1_Transformadores

APRESENTAÇÃO
Esta apostila corresponde ao primeiro capítulo do curso de Eletrotécnica, o qual tem como
finalidade introduzir ao aluno do curso de Engenharia Produção os principais fundamentos da
Eletrotécnica, de maneira simples e prática. Todos os assuntos do curso serão voltados ao chão de
fábrica, ou seja, terão uma abordagem mais técnica, e não somente focada na engenharia.
PROFESSOR: Leonardo Jose Amador Salas Maldonado
EMENTA:
Circuitos de corrente contínua: série, paralelo e misto. Voltímetros. Amperímetros. Corrente
alternada. Transformadores. Circuitos magnéticos. Eletroímã. Máquinas de corrente contínua.
Máquinas de corrente alternada. Alternadores. Motores monofásicos e trifásicos. Ensaios elétricos de
instalação. Chaves magnéticas. Disjuntores. Acessórios para iluminação.
Introdução:
SEGUNDA GUERRA MUNDIAL
Tratado de Versalles > Engenharia de produção
Ferdinand Porsche –

Professor Doktor Ingenieur Honoris Causa (Dr. h.c. Ing.)
(Maffersdorf, 3 de setembro de 1875 — Stuttgart, 30 de janeiro de 1951)
2
Produção industrial segunda guerra
Engenharia no ano século XXI - OBSOLENCIA PROGRAMADA
Procura de uma solução de engenharia
NÃO MUITO BOA
Conhecida como “Centennial Light Bulb”, ou lâmpada centenária, ela está localizada em uma central
de bombeiros na Califórnia e foi instalada em 1901. Desde então, a lâmpada de 60 watts funciona 24
horas por dia, operando com cerca de 4 watts. A data exata do início de seu funcionamento não é
conhecida, mas o aniversário do curioso objeto acontece no dia 18 de junho.
3
O problema de Europa é o problema mundial:
“Comprar coisas que não preciso com dinheiro que não tenho “ > Agiotagem bancário
Uma breve História
No século XVIII o francês Alejandro Volta inventou a pilha, com isto os físicos da época dispuseram
de uma nova forma de energia, a energia elétrica limpa e fácil de transmitir .
A corrente continua resultou ser tão útil que primeiramente substituiu os sistemas de iluminação a gás,
e posteriormente, com o invento do motor elétrico, se utilizou também como uma fonte motriz. Em
1838, Samuel Morse inventor do telégrafo começa a utilizar a corrente continua para a transmissão de
dados.
O problema que a energia elétrica em corrente continua apresentava era a transmissão a longas
distâncias devido a que sua perda era significativa, estas são conhecidas por perdas de linhas ou
perdas por efeito Joule, as quais dependem da corrente e a resistência do material condutor.
A solução técnica da época foi mudar de corrente continua para alternada já que esta permite a
utilização de transformadores.
4
Nikola Tesla (Eng elétrico Yugoslavo)
Veja como é um sistema de transmissão de energia elétrica:
[Ver filminho.]
5
Definição de transformador:
É um equipamento estático que transfere energia entre seus enrolamentos provocando a variação
dos valores de tensão e corrente mantendo os valores de potência e de freqüência constantes.
Constituído de dois enrolamentos e um núcleo que os interliga magneticamente.
Leis fundamentais do eletromagnetismo
Experiência de Oersted:
“Todo condutor percorrido por uma corrente elétrico cria em torno de si um campo magnético”.
Lei de Faraday:
“Todo condutor mergulhado em um campo magnético variável terá em seus terminais uma fem
(força eletromotriz) induzida”.
e(t) = - N
d
dt
onde: N = número de espiras
d
= variação do fluxo magnético no tempo
dt
6
Lei de Lenz:
“A corrente que aparece em um circuito elétrico fechado, em função de uma fem (força
eletromotriz) induzida, tem sentido tal a anular a causa que lhe deu origem”.
7
A energia elétrica é utilizada de duas formas, continua e alterna.
Corrente Contínua:
É a corrente que passa através de um condutor ou de um circuito elétrico somente em um sentido.
Uma fonte de tensão contínua pode variar o valor de sua tensão de saída, mas se a polaridade for
mantida a corrente fluirá somente em um sentido.
Corrente Alternada:
São correntes que possuem picos positivos e negativos passando por um valor nulo num intervalo
de tempo.
8
Leis fundamentais da corrente continua
Lei de Ohm
A lei de OHM é uma fórmula matemática que estabelece a relação entre as três grandezas
fundamentais da eletricidade: a corrente, a resistência e a tensão (tensão : também conhecida como
diferença de potencial). Foi descoberta pelo alemão George S. Ohm.
As grandezas elétricas são representadas por símbolos (letras), veja a seguir:
Grandeza
tensão
Símbolo
U ou V
Unidade
Volt (V)
corrente
I
Ampère (A)
resistência
R
Ohm (Ω)
potência
P
Watts (W)
Tensão
A diferença de potencial entre os terminais de um circuito é igual ao produto da resistência desse
circuito pela intensidade da corrente elétrica que passa por tal circuito.
Corrente
A intensidade da corrente elétrica que percorre o circuito é igual à divisão da diferença de
potencial entre os terminais desse circuito pela resistência que esse circuito apresenta à passagem da
corrente elétrica.
I=V/R
Resistência
A resistência que um circuito, apresenta a passagem da corrente elétrica é igual à divisão da
diferença de potencial (tensão) entre os terminais desse circuito pela intensidade da corrente que por ele
passa.
Veja como fica a representação da lei de OHM através de uma fórmula matemática:
R=V/I
9
Potência
A potência elétrica corresponde a um triangulo onde temos 3 componentes , a hipotenusa chamada
de potencia aparente em VA , o cateto adjacente , chamada de potencia ativa em watt e o cateto oposto
chamada de potencia reativa em VAR .
O ângulo formado entre a hipotenusa e o cateto adjacente se conhece como  e seu coseno  como fator
de potencia. Quando o ângulo entre a tensão e a corrente e zero o fator de potencia é unitário nesta
condição a potencia aparente se iguala a potencia ativa.
Exemplo “ O chuveiro
Leis de Kirchhoff
As Leis de Kirchhoff são empregadas em circuitos elétricos mais complexos, como por exemplo
circuitos com mais de uma fonte de resistores estando em série ou em paralelo. Para estudá-las vamos
definir o que são Nós e Malhas:
Nó: é um ponto onde dois (ou mais) condutores são ligados.
Malha: é qualquer caminho condutor fechado.
10
Fig. 1: Circuito com várias malhas e nós
Analisando a figura 1, vemos que os pontos a e d são nós, mas b, c, e e f não são. Identificamos
neste circuito 3 malhas definidas pelos pontos: afed, adcb e badc.
Primeira lei de Kirchhoff (lei dos nós)
Em qualquer nó, a soma das correntes que o deixam(aquelas cujas apontam para fora do nó) é
igual a soma das correntes que chegam até ele. A Lei é uma conseqüência da conservação da carga total
existente no circuito. Isto é uma confirmação de que não há acumulação de cargas nos nós.
Segunda lei de Kirchhoff (lei das malhas)
A soma algébrica das forças eletromotrizes (f.e.m) em qualquer malha é igual a soma algébrica
das quedas de potencial ou dos produtos iR contidos na malha.
Aplicando as leis de Kirchhoff
Exemplo 1: A figura 1 mostra um circuito cujos elementos têm os seguintes valores:
E1=2,1 V, E2=6,3 V, R1=1,7 Ώ, R2=3,5 Ώ. Ache as correntes nos três ramos do circuito.
11
Fig. 1: Circuito com várias malhas e nós
Solução: Os sentidos das correntes são escolhidos arbitrariamente. Aplicando a 1ª lei de Kirchhoff
(Lei dos Nós) temos:
[Fazer exemplo]
i1 + i2 = i3
Geração da tensão alternada
Funcionamento do gerador elementar, que é um tipo de fonte de fem, gera a corrente
alternada. É dito elementar por ser um modelo simplificado dos grandes geradores. No entanto seu
princípio de funcionamento é o mesmo que dos geradores encontrados em grandes usinas.
12
FIGURA 1 – GERADOR ELEMENTAR
E da forma de onda resultante do processo de geração que se obtém a fórmula da Tensão
Instantânea:
e  Emáx  sen
A equação e  Emáx  sen é também válida quando tratamos de corrente. Neste caso a
equação fica:
i  I máx  sen
Observe que são utilizadas letras minúsculas (e,i) para denotar uma grandeza na forma
instantânea.
Conceitos sobre a tensão senoidais
Valor Instantâneo
V(t )  2V0 Sent => Função senoidal
Valor de pico
Vp =
2Vo
Valor de pico a pico
Vpp = 2 2Vo
Valor médio
1
Vm =
2
2

2V0 Sent.dt
0
No caso da corrente alterna Vm = 0
Valor efetiva
Ve =
1
2

2

2
2V0 Sent dt
0
No caso da expressão apresentada para a tensão instantânea Ve = V 0
13
Principio de Funcionamento do transformador:
Aplica-se uma tensão alternada (V1) ao enrolamento primário do transformador representado na
figura abaixo. Verifica-se que o enrolamento primário é um circuito elétrico fechado aparecendo então
uma corrente I0 denominada de corrente de excitação. Esta corrente cria no enrolamento primário um
fluxo magnético variável (-
d
), conforme prediz a experiência de Oersted, que circulará pelo caminho
dt
de menor relutância oferecida pelo núcleo, cortando assim o enrolamento secundário originando uma fem
(força eletromotriz) induzida, conforme prevê a Lei de Faraday.
Observe que para facilitar a explicação, considera-se que:

O transformador é ideal, isto é, sem perdas internas;

O secundário está em aberto (sem carga), logo sem circulação de corrente.
Relações do Transformador ideal
Da lei de Faraday tem-se:
e(t) = - N
d
, aproximando e(t) = V(t)
dt
Então:
V1= - N 1
d
(primário)
dt
V2 = - N 2
=>
V
d
= 1
dt
N1
V
d
d
(secundário) =>
= 2
dt
dt
N2
Assim
V1
V
= 2
N1
N2
Por tanto:
V
N
1  1
V
N
2
2
14
Do Conceito de Potência
A potência primária (S1)e a secundaria (S2) no transformador ideal é considerada iguais
Isto é S1 = S2
, ou seja,
V1 I1 = V2 I2
=>
V
I
1  2
V
I
2
1
Associando as equações já vistas, tem-se:
V
N
I
1  1  2
V
N
I
2
2
1
= a = relação de transformação
Exercícios:
Em um transformador, o lado primário possui uma tensão de 220 volts e uma corrente de 6 Ampéres,
enquanto que o lado secundário possui uma corrente de 32 Ampéres. Pede-se o valor da tensão no
lado secundário deste transformador.
Termos utilizados em transformadores:
Transformador Monofásico:São transformadores que possuem apenas um conjunto de bobinas de Alta
e Baixa tensão colocado sobre um núcleo.
Diagrama de um transformador monofásico
Disposição real das bobinas
15
Transformadores Trifásicos:
São transformadores que possuem três conjuntos de bobinas de Alta e Baixa tensão colocadas sobre
um núcleo. O funcionamento é idêntico a um transformador monofásico, uma vez que a sua constituição
é de três transformadores monofásicos entre si.
Tensão Nominal:São valores de tensão projetados e especificados pelo fabricante para
funcionamento adequado do equipamento. Sempre que ligar um transformador deve-s observar as suas
tensões nominais e e compará-las com tensões de linha e de carga para não danificar qualquer elemento
do circuito.
Enrolamento Primário:É o enrolamento do transformador que recebe a energia.
Enrolamento Secundário:É o enrolamento do transformador que fornece a energia a uma carga.
16
Enrolamento de Alta Tensão (AT):É o enrolamento do transformador que possui maior valor de
tensão nominal.
Enrolamento de Baixa Tensão (BT):É o enrolamento do transformador que possui menor valor de
tensão nominal.
Transformador Elevador:São os transformadores que elevam os valores de tensão recebidos, isto
é, o enrolamento primário coincide com o enrolamento de baixa tensão.
Transformador Abaixador:São os transformadores que abaixam os valores de tensão recebidos,
isto é, o enrolamento primário coincide com o enrolamento de alta tensão.
Potência Nominal:É a máxima potência que pode ser transferida do enrolamento primário para o
enrolamento secundário sem danos ao equipamento. Esta potência é especificada pelo fabricante e deve
ser contida na placa de identificação. É fornecida em VA, KVA, MVA.
Corrente Nominal:É o valor de corrente que circula em um enrolamento quando o transformador
estiver trabalhando com potência e tensão nominal.
Freqüência Nominal:É a freqüência para qual o equipamento foi projetado e fabricado. No caso
do Brasil é de 60 Hz.
Classe de isolamento:É a classe que determina o valor da temperatura que os componentes do
transformador devem suportar sem sofrerem alterações em suas características. É dada em 0C.
Classe de tensão de isolamento:É a classe que determina o valor de tensão que os componentes
devem suportar sem danos as suas características iniciais. É dado em KV. ,assim a tensão de alimentação
do transformador de distribuição é de 13,8 KV e a classe de tensão de isolamento é de 15 KV.
Parte Ativa:Formada pelos bobinados primários e secundários.
17
Impedância %:É um valor percentual que indica a queda de tensão produzida internamente em um
transformador, dando também a ideia das perdas internas.
Corrente de Excitação:É a corrente que circula em um enrolamento do transformador quando este
é alimentado com sua tensão nominal e o outro enrolamento está aberto. É representado por I0 e é dada
em % da corrente nominal, sendo responsável pela produção do fluxo magnético e suprir perdas no
núcleo. (usualmente não superior a 6% da corrente nominal.)
Correntes Parasitas ou Correntes de Foucault:Sendo o núcleo feito de um material condutor e
este mergulhado em um campo magnético variável, segundo a Lei de Faraday, nele deverá induzir forças
eletromotrizes. Considerando o núcleo como um circuito fechado nele aparecem correntes que são
chamadas de correntes parasitas.
Estas correntes, por sua vez provocam perdas por aquecimento no núcleo. Para reduzir o valor desta
corrente deve-se aumentar a resistência elétrica a sua laminação e isolação das chapas. Pode-se também,
com este intuito, adicionar 4% de silício a composição das chapas.
18
Ferro maciço
Ferro laminado
Histerese:Pode-se entender como a resistência que as partículas de um material ferromagnético
oferece as mudanças de polaridade de um campo magnético.
Autotransformador:Um transformador pode ser constituído por um único enrolamento, sendo
assim, o primário coincide com o secundário. Este tipo de transformador denomina-se de
autotransformador, representado abaixo. Ele possui maior rendimento e pequenas perdas de capacidade
em KVA, porém se usados para grandes variações de tensão estaremos sacrificando os itens de
isolamento do primário e secundário.
Rendimento de um autotransformador:É a relação entre a potência que uma máquina fornece e
a potência que a mesma recebe, podendo ser dado por:
η=
PotênciaSecundária
x 100%
Potência Pr imária
Os transformadores são os aparelhos que apresentam os maiores rendimentos.
PolaridadeÉ a marcação existente nos terminais (dos enrolamentos) dos transformadores indicando
o sentido da circulação de corrente em um determinado instante em conseqüência do sentido do fluxo
produzido.
19
20
Transformador de Potência a Óleo :Os transformadores comumente utilizados na distribuição
são do tipo imerso em óleo mineral, extraído do petróleo. Esses transformadores estão colocados em
tanques cheios de óleo com radiadores para melhorar a troca térmica com o médio por efeito da
convecção na superfície irradiadora .
As ligações do transformador devem ser realizadas de acordo com o diagrama de ligação de sua
placa de identificação. É importante que se verifique se os dados da placa de identificação estão
coerentes com o sistema ao qual o transformador vai ser instalado.
Com a finalidade de adequar a tensão do transformador à tensão de alimentação, o transformador é
dotado de derivações (tap’s) que podem ser escolhidos mediante a utilização de um painel de ligações ou
comutador.
O tanque deverá ser efetiva e permanentemente aterrado. Uma malha de terra permanente de
baixa resistência é essencial para uma proteção adequada.
A malha de terra deverá ser ligada a esses conectores por meio de um cabo nú de cobre de bitola
adequada e a mais curta possível.
Acessórios.
Desumidificador de Ar (Sílica-Gel): A fim de que sejam mantidos elevados os índices dielétricos
do óleo dos transformadores estes são equipados com secadores de ar que absorvem a umidade do ar
aspirado e que flui para o transformador.
21
Rele de Gás (tipo Buchholz):O relé Buchholz (figura abaixo) tem por finalidade proteger aparelhos
elétricos que trabalham imersos em líquido isolante, detectando as descargas parciais geradas pela
isolação defeituosa do enrolamento, do ferro ou mesmo contra a terra, podem causar avarias de grande
monta caso o defeito permaneça despercebido do operador durante algum tempo.
RELE BUCHOLTZ
Termômetro com Contatos; Com haste rígida ,este termômetro possui dois ponteiros de ligação
e um de indicação de temperatura máxima atingida em determinados períodos.
Indicador de Nível de Óleo: Os indicadores magnéticos de nível tem por finalidade indicar o nível
de óleo dielétricos, são providos de contatos para alarme NF e NA.
22
.
Tubo de Explosão:Destina-se a proteger o transformador contra sobre pressão súbita.
Consiste basicamente de um tubo que de um lado é conectado ao tanque do transformador e no
outro lado possui um disco de ruptura.
Em caso de súbita elevação de pressão que ultrapasse o valor de ruptura do disco haverá o
rompimento com abertura total da sessão de passagem fazendo a pressão cair rapidamente sem danificar
outras partes do transformador.
Válvula de Alívio de Pressão:A válvula de alívio de pressão de fechamento automático é instalada
em transformadores imersos em líquido isolante com a finalidade de protegê-los contra possível
deformação ou ruptura do tanque, em casos de defeito interno com aparecimento de pressão elevada. A
válvula é extremamente sensível e rápida (opera em menos de dois milésimos de segundo), fecha-se
automaticamente após a operação impedindo assim a entrada de qualquer agente externo no interior do
transformador.
Relé de Pressão Súbita:O relé de pressão súbita é um equipamento de proteção para
transformadores do tipo selado, é instalado acima do nível máximo do líquido no espaço com gás
compreendido entre o líquido e a tampa do transformador.
O relé é projetado para atuar quando ocorrem defeitos no transformador que produzem pressão
interna anormal sendo sua operação ocasionada somente pelas mudanças rápidas da pressão interna
independente da pressão de operação do transformador.
Para aumentos de pressão de 0,4 atm/seg o relé opera em cerca de 3 ciclos. Para aumentos de
pressão mais rápidos (1 atm/seg) a operação dá-se em menos de um ciclo.
23
Subestação Aérea
Obs 1US$ = 2.8R$
Subestação abrigada
24
Sub estação, muro corta fogo e poço
25
MUFAS
Valvula de pressão
Tanque de expansão
Termometro
Secador
26
Características do Oleo
Obs . No caso de oleos minerais ( derivados do pertroleo)
Termografia de transformador
<Filminho do trafo>
28
Transformador de potencia a seco
Neste caso o transformador não tem líquido isolante, são constituídos segundo os mesmos
princípios que os transformadores isolados com óleo, porém não há líquido isolante. Os materiais
isolantes dos enrolamentos são substituídos por outros de maior resistência ao calor e os enrolamentos
ficam expostos.
Pode haver uma proteção mecânica, constituída por um invólucro com aberturas para permitir a
circulação do ar por convecção térmica a fim de esfriar o enrolamento.
Simbologia das conexões
Variador de Tensão Monofásico (Varivolt
Monofásico)
Transformador Trifásico Ligado em
Triângulo-Estrela
Transformador Trifásico Ligado em
Estrela-Estrela
29
Transformador Trifásico Ligado em
Triângulo-Triângulo
Transformador Trifásico Ligado em
Estrela-Triângulo
Transformador Monofásico de
Distribuição Rural
30
Transformadores de medição :Os transformadores para instrumentos são equipamentos
projetados e construídos especificamente para alimentarem instrumentos elétricos de medição, controle
e proteção. A função dos TI é a redução da magnitude da tensão ou da corrente em uma proporção
definida, mantendo a posição vetorial.
Transformador de Potencial (TP):É um transformador cujo enrolamento primário é conectado
em derivação com o circuito principal sendo seu enrolamento secundário destinado a alimentar seus
sensores de potencial dos instrumentos elétricos de medição, controle ou proteção. Sua principal
função é reduzir a tensão do circuito principal para valores facilmente mensuráveis.
Os TP’s são projetados para uma tensão secundária padrão de 115 volts.
31
Exemplo: Determinar a indicação obtida em um voltímetro ligado a um TP, de relação de
transformação 13.800/115 V, se o primário estiver ligado a uma rede de 13.200 volts.
Montando uma regra de três:
13.800 ...............115
13.200 ............... x
x = 110 volts, logo a leitura será de 110 volts.
Transformador de Corrente (TC):É um transformador cujo enrolamento primário é conectado
em serie com o circuito principal sendo seu enrolamento secundário a alimentar os sensores de
corrente dos instrumentos elétricos de medição, controle ou proteção. Sua principal função é reduzir a
corrente do circuito principal para valores facilmente mensuráveis.
O secundário de um TC esta padronizado para uma corrente nominal de 5A.
Nas figuras abaixo vê-se os diferentes formatos dos TCs:
32
Exemplo: Um amperímetro ligado ao secundário de um TC de relação de transformação 200/5
A, indica uma leitura de 3,75 Ampéres, qual a corrente que circula pela linha?
Montando uma regra de três:
200 ............ 5
x ................ 3,75
x = 150 Ampéres, logo a corrente na linha é de 150 Ampéres.
Obs. o secundário de um TCs nunca deve ficar sem carga, pois apresenta uma alta tensão em
seus terminais o que pode originar uma falha no isolamento.
33
Geração elétrica num sistema trifásico
De forma similar à geração monofásica se tem a geração trifásica , neste caso temos 3 bobinas
deslocadas 120°, assim as tensões geradas também também estarão deslocas 120°
Expressões de tensão em função do tempo e em forma de fasor
V1  2 * 220Sent
V1  2 * 2200
V2  2 * 220Sen[t  120]
V2  2 * 220120
V3  2 * 220Sen[t  240º ]
V3  2 * 220240
34
No caso de ligação estrela
VAB  [V1  V2 ] V1  2 * 2200
V1  2 * 2200
=> V1  2 * 220 cos t  j * 2 * 220Sent
- V2  2 * 220120 =>  V2   2 * 220 cos t  j * 2 * 220Sent
VAB  [V1  V2 ] =
3 * 2 * 220  30
Exemplo 1
35
Exemplo 2
Exercicios com fasores
36
Exercício
De mostre o potencial do ponto neutro
Tensão de Linha (VL): É a tensão entre duas linhas na rede de alimentação do circuito,
independe da conexão deste circuito.
Tensão de Fase (VF):É a tensão aplicada sobre o elemento do circuito, logo depende da conexão
feita.
Corrente de Linha (IL): É a corrente que circula na rede de alimentação do circuito independe
da conexão deste circuito.
37
Corrente de Fase (IF): É a corrente que circula no elemento de um circuito, logo, depende da
conexão deste circuito.
Conexão Triângulo (∆):
De mostre as equações
VL = VF
IL = IF .
3
Conexo Estrella (Y):
Demostré as equações
VL = VF .
3
IL = IF
38
Potencia trifásica balanceada
Potência complexa
Utilizando as ferramentas fasoriais também pode-se calcular as potências aparente, ativa e
reativa.
Seja A tensão efetiva Vef  Vef  v V
E a corrente efetiva I ef  I ef  i A
No caso da potência deve-se considerar a defasagem entre a tensão e a corrente, isto é, a
diferencia entre o ângulo da tensão e a corrente, assim para o cálculo da potência considera-se o
complexo conjugado da corrente , definido como I ef  ief    i
A expressão para a potência S = Vef  v ief    i =
Vef I ef  v   i
Onde a expressão  v   i corresponde a defasagem
Portanto, a potência ativa corresponde a parte real do produto
Vef  v ief    i e a parte
reativa corresponde á parte imaginaria de este produto.
39
Triângulo de Potência
Potência Aparente (S): Corresponde ao produto do valor efetivo da tensão por o valor
efetivo da corrente formando a hipotenusa do triângulo.
Sua unidade é o VA, também existem seus múltiplos os KVA e os MVA.
Smono = V . I
Strifásico =
3 .V.I
Φ = defasagem
cos Φ = fator de potência
Potência Ativa (P): É a potência que realmente é transformada em trabalho, sua unidade é o W
seus múltiplos KW, MW.Pmono = V . I . cos Φ
Ptrifásico =
3 . V . I . cos Φ
Potência Reativa (Q): É a potência que não produz trabalho mecânico, porém é
obrigatoriamente consumida na geração dos campos magnéticos dos bobinados.
Sua unidade é o Var, seus múltiplos Kvar, MVar.
Qmono = V . I . sen Φ
Qtrifásico =
3 . V . I . sen Φ
Ex Placa de motor
40
[ Atividade pratica]
Questão 1
Nome do fabricante ...................................................................................................
Normas utilizadas .....................................................................................................
Numero de fases .......................................................................................................
Tipo de carcaça ( Frame) ...........................................................................................
Data de fabricação ....................................................................................................
Identificação do projeto do motor ( protocolos de fabricação) ..................................
Freqüência .................................................................................................................
Categoria de torque ..................................................................................................
Potencia (CV/Kw) .....................................................................................................
Rotação do motor ......................................................................................................
Fator de serviço ( sobrecarga) ...................................................................................
Classe de isolamento ...................................................................................................
Elevação de temperatura ............................................................................................
41
Relação entre a corrente de partida e a nominal .......................................................
Grau de proteção contra corpos sólidos ....................................................................
Grau de proteção contra líquidos ...............................................................................
Tensões de trabalho ...................................................................................................
Correntes de trabalho .................................................................................................
Regime de serviço .....................................................................................................
Máxima temperatura ambiente ..................................................................................
Altura máxima ............................................................................................................
Desenhe as conexões para 380 e 220V
....................................................................................................................
Numero dos rolamentos (abertos ou obturados) .........................................................
Tipo de graxa e quantidade ...........................................................................................
Peso do motor .............................................................................................................
Rendimento ................................................................................................................
Fator de potencia .......................................................................................................
Homologação ...............................................................................................................
Curiosidades
Elementos de rodagem
Temperatura máxima 120º
42
43
44
Mudanças de triangulo-estrella
Sistemas desbalanceados
Comportamento da corrente nos componentes mais usuais num sistema elétrico
Na resistência Ir =
V(t )
Na indutância IL=
Capacitância
R
1
V( t ) dt
L
Ic = C
dV( t )
dt
Como a tensão V(t )  2V0 Sent , podemos concluir que a corrente Ir esta em fase com a
tensão. (multiplicação por escalar) , isto é:
Ir =
1
2V0 Sent
R
45
Como a corrente num indutor é a integral da uma onda senoidal, isto é - cos t
A expressão fica:
IL = 
1
 2V0 cos t
L
Isto é existe uma defasagem de 90° em atraso com a tensão V(t).
Já no caso do capacitor a corrente corresponde à derivada de uma onda senoidal, isto é + cos t
I c = C 2V0 cos t
Isto é a corrente esta adiantada 90° com relação à tensão V(t).
Nota: a defasagem a que se faz referência só existe pelo fato de ser uma função senoidal, caso
seja uma outra função não será aplicável.
Reapresentação no plano complexo:
A impedância nos circuitos elétricos
Viu-se a expressão da corrente através dos componentes mais usuais num sistema elétrico:
Na resistência Ir =
Na indutância IL=
Capacitância
V(t )
R
1
V( t ) dt
L
Ic = C
dV( t )
dt
É importante encontrar e expressão das resistências que cada componente apresenta ao circuito,
lembrando a lei de Ohm:
R=
V
i
46
De forma análoga encontra-se uma expressão para a resistência de um indutor e um capacitor,
para isto utiliza-se a transformada de Laplace uma ferramenta matemática que nos permitirá este
cálculo.
Aplicando a transformada de Laplace a nossas equações:
Na resistência
Ir =
V(t )
R
/
=> Ir (s ) =
V( s)
R
=> R =
V( s )
Ir( s )
Na indutância
IL=
V( s )
1
1
V
dt
V
/
=>
I
=
=>
Z
=
= Ls = j L = jX L = X L   90

L(s)
L
(
t
)
(
s
)
I L(s)
L
Ls
Capacitância
Ic = C
dV( t )
dt
/  => Ic (s ) = Cs V(s ) => Zc =
V( s )
I c(s)
=
1
1
1
j = -j X c = X c   90
=
=Cs
C
jC
Onde S = j  e por sua vês   2f , no caso do Brasil f= 60Hz
Análise de circuitos através de fasores
Com os conceitos de impedância e fasores analisaremos os diferentes circuitos típicos
Circuito RL série
Diagrama fasorial
47
cos  
E 2  VR2  VL2
VR
E
sen 
VL
E
tan  
VL
VR
Podemos também obter um diagrama de impedâncias. Basta fazer a divisão das tensões
pela corrente.
VR
R
I
VL
 XL
I
E
Z
I
Z é a oposição total oferecida a passagem da corrente e é dada em ohms (Ω).
O diagrama de impedâncias ficará então:
cos  
Z 2  R 2  X L2
R
Z
sen 
XL
Z
tan  
XL
R
Exemplo: para o circuito a seguir, calcular a corrente e as quedas de tensão, montando o
diagrama fasorial:
X L  2    f  L  X L  2    60  200  10 3  X L  75,4 
Z  R 2  X L2
I
 Z  60 2  75,4 2
 Z  96,4 
E
100
 I
 I  1,04 A
Z
96,4
VR  R  I  VR  60 1,04  VR  62,4 V
VL  X L  I  VL  75,4 1,04  VL  78,4 V
48
cos  
R
60
 cos  
 cos   0,622
Z
96,4
  51,5
Exemplo: para o circuito abaixo, calcular o valor das potências ativa, reativa e aparente e
montar o triângulo de potências.
tan  
VL
VR
I
 VR 
VR
R
100
 VR  100 V
tan 45
 I
100
 I 2A
50
P  I 2  R  P  2 2  50  P  200 W
Q  VL  I  Q  100  2  Q  200 VAr
S  P2  Q2
 S  200 2  200 2
 S  282,8 A
49
Circuito RC série
Sabemos que VR está em fase com a corrente e VC está atrasada 90º da corrente. Sabemos
também que a soma fasorial de VR e VC nos dá a tensão aplicada E.
Podemos extrair as seguintes relações:
E 2  VR2  VC2
cos  
VR
E
sen 
VC
E
tan  
VC
VR
Dividindo-se todos os componentes do diagrama pela corrente, temos:
VR
R
I
VC
 XC
I
E
Z
I
Logo, o diagrama de impedâncias será:
Donde:
Z 2  R 2  X C2
cos  
R
Z
sen 
XC
Z
tan  
XC
R
50
Exemplo: calcular a corrente, o ângulo de fase e as quedas de tensão no circuito abaixo,
montando o diagrama fasorial.
XC 
1
1
 XC 
 X C  132,7 
2   f  C
2    60  20  10 6
Z  R 2  X C2
I
 Z  70 2  132,7 2  Z  150 
E
120
 I
 I  0,8 A
Z
150
VR  R  I  VR  70  0,8  VR  56 V
VC  X C  I  VC  132,7  0,8  VC  106,2 V
cos  
R
70
 cos  
 cos   0,467    62,2
Z
150
Potências
S V I
tan  
S 2  P2  Q2
Q  V  I  sen
P  V  I  cos 
Q
sen 
S
cos  
P
S
S  I2 Z
Q
P
V R2
P
R
P  VR  I
V2
S
Z
Q  VC  I
P  I2 R
Q  I 2  XC
51
Triângulo de potências
O triângulo de potências para um circuito RC série só difere do circuito RL série pela posição em
que fica a potência reativa. Vimos que no circuito RL a potência reativa é positiva. No circuito RC série, ela
é negativa.
Exemplo: calcular as potências ativas, reativa e aparente, montando o triângulo de potências para
o circuito abaixo:
XC 
1
1
 XC 
 X C  88,4 
2   f  C
2    60  30  10 6
Z  R 2  X C2
I
 Z  120 2  88,4 2  Z  149,05 
E
220
 I
 I  1,476 A
Z
149,05
S  E  I  S  220  1,476  S  324,7 VA
P  I 2  R  P  1,476 2  120  P  261,5 W
Q  I 2  X C  Q  1,476 2  88,4  Q  192,6 VAr
cos  
R
120
 cos  
 cos   0,805    36,4
Z
149,05
52
Circuito RLC série
O circuito RLC série é uma composição em série dos três tipos de circuitos puros.
Diagrama fasorial
Deste diagrama, podemos extrair as relações trigonométricas para o circuito RLC série.
sen 
VL  VC
E
cos  
tan  
VR
E
VL  VC
VR
E 2  VR2  VL  VC 
2
Dividindo-se todos os elementos do diagrama pela corrente, teremos o diagrama de impedâncias.
53
sen 
XL  XC
Z
cos  
tan  
R
Z
XL  XC
R
Z 2  R 2  X L  X C 
2
Exemplo: calcular a corrente, todas as quedas de tensão e montar o diagrama fasorial para o
circuito abaixo:
X L  2    f  L  X L  2    60  0,2  X L  75,4 
XC 
1
1
 XC 
 X C  132,7 
2   f  C
2    60  20  10 6
Z  R 2  X L  X C 
2
 Z  100 2  75,4  132,7
I
E
150
 I
 I  1,3 A
Z
115,3
2
 Z  115,3 
VR  R  I  VR  100 1,3  VR  130 V
VL  X L  I  VL  75,4 1,3  VL  98,1 V
VC  X C  I  VC  132,7  1,3  VC  172,5 V
cos  
R
100
 cos  
 cos   0,865
Z
115,3
  29,9
54
Potências no circuito RLC série
QC  VC  I  I 2  X C 
VC2
XC
QL  V L  I  I 2  X L 
VL2
XL
QC = potência reativa capacitiva (VAr)
QL = potência reativa indutiva (VAr)
A potência reativa total (Q) é dada por:
Q  QL  QC
Ou:
Q  E  I  sen  S  sen  VL  VC   I  I
2
VL  VC 2
 X L  X C  
X L  X C 
Exemplo: no circuito abaixo, calcular as potências ativa, reativa e aparente e montar o triângulo
de potências:
55
Z  R 2  X L  X C 
2
I
 Z  40 2  60  30
2
 Z  50 
E
100
 I
 I 2A
Z
50
P  I 2  R  P  2 2  40  P  160 W
QL  I 2  X L  QL  2 2  60  QL  240 VAr
QC  I 2  X C
Q  QL  QC
 Q C  2 2  30  Q C  120 VAr
Q  240  120  Q  120 VAr
S  E  I  S  100  2  S  200 VA
cos  
R
40
 cos  
 cos   0,8    36,87
Z
50
Associações de componentes
Resistência equivalente
56
Indutância equivalente
Le  L1  L2  L3
X Le  X L1  X L 2  X L3
Le = indutância equivalente (H)
XLe = reatância indutiva equivalente (Ω)
L1, L2, L3 = indutâncias componentes (H)
XL1, XL2, XL3 = reatâncias indutivas componentes (Ω)
Na associação em paralelo, temos:
Para duas indutâncias:
Le 
L1  L2
L1  L2
X Le 
X L1  X L 2
X L1  X L 2
Capacitância equivalente
A capacitância equivalente de associação paralela é dada pela soma das capacitâncias
componentes. A reatância capacitiva equivalente é calculada pelas mesmas fórmulas da resistência em
paralelo, ou seja:
Ce  C1  C2  C3    Cn
X Ce 
1
1
1
1
1



X C1 X C 2 X C 3
X Cn
57
Ce = capacitância equivalente (F)
XCe = reatância capacitiva equivalente (Ω)
C1, C2, C3, Cn = capacitâncias componentes (F)
XC1, XC2, XC3, XCn = reatâncias capacitivas componentes (Ω)
Para duas reatâncias:
X Ce 
X C1  X C 2
X C1  X C 2
Na associação série, a capacitância e a reatância capacitiva são dadas por:
Ce 
1
1
1
1
1



C1 C2 C3
Cn
X Ce  X C1  X C 2  X C 3    X Cn
Para duas capacitâncias:
Ce 
C1  C 2
C1  C 2
Modelo real do transformador (parâmetros do transformador)
Relação de Transformação
É a relação que existe entre a tensão ou corrente do primário e a tensão ou corrente do secundário de
um transformador.
58
Para o transformador a vazio, tem-se o que se convencionou a chamar de relação de transformação
teórica;
a=
E1
(1)
E2
Em que E1 e E2 são os valores eficazes das fem (forças eletromotrizes) induzidas nos enrolamentos
primário e secundário respectivamente. A partir da figura acima se pode construir o circuito equivalente de
um transformador a vazio, mostrado abaixo:

i1
r1
x1
r2
u1
x2
i2
u2
Z
Onde:
r1 → resistência do enrolamento primário;
x1 → reatância de dispersão do enrolamento primário=2 f L1
E1 → fem (força eletromotriz) induzida no primário;
r2 → resistência do enrolamento secundário;
x2→ reatância de dispersão do enrolamento secundário=2 f L2
E2 → fem (força eletromotriz) induzida no secundário.
Modelo real do transformador
Portanto
Re1 = (R1 + a2 R2)
Re1 = 2a2R2 = 2R1, do mesmo jeito para a reatância indutiva equivalente:
XLe1 = 2a2XL2 = 2XL1
59
Re1
2a 2
R2 =
R1 =
XLe1
2a 2
XL2 =
XL1 =
Re1
2
XLe1
2
Os valores R e1 , XL e1 e Z e1 são determinados pelos ensaios em curto circuito e circuito aberto de
transformador.
Determinação dos parâmetros no ensaio de curto circuito
Para o circuito primário tem-se uma corrente de curto circuito Icc medida e uma tensão de curto
circuito Vcc mede-se também a potência de curto circuito.
Ze 1 =
Vcc
I cc
Impedância equivalente primária calculada a partir dos valores de corrente e tensão
na condição de curto circuito
Pcc = I2cc Re1
Re1 =
=> Da potência de curto circuito podemos calcular Re1
Pcc
I cc2
Ze1 =
Re1  XLe1
XLe1 =
2
2
Z e1  Re1 => Podemos calcular a reatância indutiva primária
2
2
Os parâmetros do transformador em função dos valores obtidos no ensaio de curto circuito e circuito
aberto:
2a2R2 = Re1
2R1 = Re1
2a2XL2 = XLe1
2XL1 = XLe1
60
Determinação dos parâmetros no ensaio de circuito aberto
Como vemos no desenho do modelo de transformador real existe uma corrente de magnetização,
necessária para que o transformador trabalhe, a potência dissipada por esta corrente é chamada de perdidas
de ferro.
Como o fio de cobre apresenta uma resistência ôhmica pura ao circular uma corrente por ela se produz
uma potência por efeito Joule I2Rcu, esta potência perdida no cobre depende da magnitude da corrente que
circula. No entanto a perda de ferro e um valor fixo.
Assim:
Pfe = Potência indicado pelo watímetro quando o transformador esta em aberto e tem um valor fixo.
Pcu = Potência dissipada no fio de cobre em função da magnitude da corrente que circula.
Com a montagem do ensaio em curto-circuito, os instrumentos permitem a obtenção de:
Pcc → Potência fornecida ao transformador em curto;
Vcc → Tensão de curto-circuito medida no enrolamento de AT;
I1n, I2n → Correntes nominais nos dois enrolamentos.
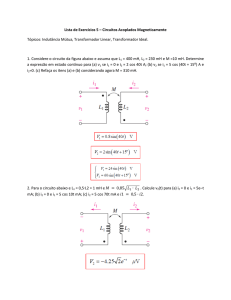
Exercícios
61
1) Calcule a tensão de entrada no primário de um transformador ensaiado a vazio com os seguintes
parâmetros:
r1 = 32 Ω
f = 60 Hz
L1 = 45 mH
I0 = 3,2 + j4,6 A
E1 = 276 - j 49 V
2) Calcule a fem (força eletromotriz) induzida no primário de um transformador ensaiado a vazio,
onde foi aplicada uma tensão de entrada de 127 + j 100 volts, dando os seguintes valores:
r1 = 2,4 Ω
x1 = 32 Ω
I0 = 7,2 – j 5,6 mA
3) Um transformador distribuição de 500kva 2300/208 , 60hz teve seus testes de aceitação constando
de um ensaio a vazio e um de curto circuito, antes de ser colocado em serviço como transformador
abaixador . A partir desses ensaios deve se calcular seus parâmetros:
Ensaio a vazio: Vob = 208V Iob= 85A Po = 1800w
Ensaio de curto circuito Vcc = 95V Icc = 217,5A Pcc=8,2kw
Valores Unitários (sistema por unidade)
O sistema "por unidade", ou, mais brevemente, sistema p.u., consiste na definição de valores de base para
as grandezas (tensão, corrente, potência, etc.), seguida da substituição dos valores das variáveis e constantes
(expressas no Sistema Internacional de unidades) pelas suas relações com os valores de base pré-definidos.
Para uma grandeza G o valor em p.u. numa base Gb obtém-se então através da expressão Gpu=G/Gb.
Exemplo 1:
62
Numa base de corrente Ib=50 A, a corrente I=30 A terá o valor I pu 
I
30

 0,6 pu
I b 50
Os cálculos serão realizados no sistema p.u., e os resultados finais novamente convertidos para o S.I. através
de G=Gpu.Gb, ou seja, multiplicando o valor em p.u. pelo valor da base.
Bases
Dadas as relações existentes entre as unidades só poderão definir-se duas bases independentes a partir das
quais se calculam todas as outras. Num sistema de energia definem-se vulgarmente como bases
independentes a potência aparente total Sb para o sistema e a tensão composta Vb num barramento
determinado.
Por sua vez, as bases de impedância e corrente calculam-se através das expressões:
Zb 
Vb2
S
, I b  b (caso monofásico)
Sb
Vb
Ib 
Sb
3Vb
(caso trifásico)
Mudança de base
O valor em pu que se deseja expressar numa outra base deve-se obter primeiramente seu valor na base atual,
após dividir-se pela base nova.
Uma aplicação imediata da expressão anterior é a transformação dos valores das características das
máquinas elétrica, habitualmente dados em percentagem dos valores nominais da máquina, para valores em
p.u. nas bases do sistema. Os dois exemplos seguintes ilustram essa aplicação.
Exemplo 2:
A reatância transitória de um alternador de 50 MVA, 10 kV é x'=12%. As bases da rede são, na zona
do alternador, Sb=100 MVA e Vb=11 kV.
Calcule seu valor em p.u. na nova base
1- Obtemos o valor na base atual
Vb2
10 2 K 2V 2
=
= 2  => X b1 = 0,12 x 2 = 0,24 
Zb 
50.000KVA
Sb
2- Calcular a nova base
Z b2
112 K 2V 2
= 1,21 

100.000 KVA

3- Expressando o valor na nova base
X b2 
0,24
 0,198 PU
1,21
Exemplo 3:
63
A reatância de fugas (ou tensão de curto-circuito, Ucc) de um transformador de 30 MVA, 60/16 kV, é
xf=8%. A base de potência da rede é Sb=50 MVA, e as bases de tensão nas zonas do primário e
secundário são, respectivamente, Vbp=56,25 kV e Vbs=15 kV.
Encontre a expressão para a reatância em p.u. usando como base a rede
1 Encontrar o valor de base usado
Zb 
Vb2
60 2 K 2V 2
=
= 120  => X f 1 = 0,08 x 120 = 9,6 
30.000KVA
Sb
2- Calcular a nova base
Z b2 
56,25 2 K 2V 2
= 63,28 
50.000KVA

3- Expressando o valor na nova base
X f2 
9,6
 0,152 PU
63,28
(Repare que igual valor se obteria se usassem 60 e 56,25 kV em vez de 16 e 15 kV).
O Autotransformador
O transformador analisado pressupõe isolação entre o primário e o secundário, existe uma outra
combinação entre as polaridades do transformador relacionando o primário com o secundário formando um
único bobinado. Esta outra disposição não só permite outras opções de tensões se não também um aumento
de potência.
Ligações de um transformador como autotransformador abaixador e elevador.
Esta nova disposição de circuitos também segue as equações dos transformadores já vistas.
64
Deve-se tomar cuidado com a corrente nas configurações abaixador e elevador.
Autotransformador como abaixador,
I2= I1 + Ic
Autotransformador como elevador
I1 = I2 + Ic
Autotransformador como elevador
Ex: Para o transformador isolado de 10KVA 1200/120 V, ligado como autotransformador com
polaridade aditiva e subtrativa.
a) A capacidade original do enrolamento de 120V em Amperes.
b) A capacidade original do bobinado do enrolamento de 1200V em Amperes.
c) A capacidade do autotransformador usando na configuração aditiva
d) Acréscimo percentual da capacidade do transformador em relação ao transformador isolado.
Utilizando o autotransformador na configuração subtrativa
a. A capacidade original do enrolamento de 120V em Amperes.
65
b. A capacidade original do bobinado do enrolamento de 1200V em Amperes.
c. A capacidade do autotransformador usando na configuração substrativa .
d. Acréscimo percentual da capacidade do transformador em relação ao transformador isolado
Autotransformador como abaixador
Repita o exemplo anterior, para o transformador isolado de 10Kva 1200/120v, ligado como
autotransformador abaixador, com polaridade subtrativa.
Exercícios:
1- Ao realizar o ensaio de curto-circuito em um transformador:
a) Por que é o lado de baixa tensão que é usualmente curto-circuitado.
c) Por que são consideradas desprezíveis as perdas no núcleo de um transformador.
d) Como se determinam as perdas no cobre na operação em curto-circuito.
e) Qual a tensão necessária para a realização do ensaio em curto-circuito.
f) Desenhe o circuito equivalente de um transformador.
g) Defina: seus parâmetros
k) Qual a influência da polaridade em transformadores monofásicos e trifásicos.
66
Polaridade em transformadores trifásicos
Isolando-se eletricamente cada uma das fases podemos realizar o teste de polaridade do mesmo modo
que para os transformadores monofásicos.
67