IME2005 - Olimpo

2005
IME
FÍSICA
“A matemática é o alfabeto com que Deus escreveu o mundo”
Galileu Galilei
Questão 01
Um canhão de massa M = 200 kg em repouso sobre um plano horizontal sem atrito é carregado com um projétil de massa
m = 1 kg, permanecendo ambos neste estado até o projétil ser disparado na direção horizontal. Sabe-se que este canhão pode ser
considerado uma máquina térmica de 20% de rendimento, porcentagem essa utilizada no movimento do projétil, e que o calor
fornecido a esta máquina térmica é igual 100.000 J. Suponha que a velocidade do projétil após o disparo é constante no interior
do canhão e que o atrito e a resistência do ar podem ser desprezados. Determine a velocidade de recuo do canhão após o
disparo.
Resolução:
Máquina térmica
η = 0,2
ET = 100.000 J
Eutilizada = ET 0,2 (Energia utilizada no projétil)
m ⋅ v2
Eutilizada =
= 20.000
2
v 2 = 40.000 ∴ v = 2 ⋅ 102 m / s (velocidade do projétil)
Durante o tiro há conservação de quantidade de movimento do sistema isolado canhão-projétil:
∑ Q0 = ∑ Q f
m ⋅ V0 + M ⋅ v0 = m ⋅ V + M ⋅ v
0 = 1 ⋅ (2 ⋅ 102 ) + 2 ⋅ 102 ⋅ v
v=
−2 ⋅ 102
= −1 m/s
2 ⋅ 102
Resposta :
v = - 1,0 m/s, sendo que o negativo indica apenas sentido contrário ao do projétil.
Questão 02
Considere um elétron de massa m e carga –e, que se move com velocidade v conforme o indicado na figura abaixo. No instante
t = 0 é ligado um campo B uniforme em todo o espaço. Desprezando a ação da gravidade, determine:
a. o trabalho realizado pela força magnética após um intervalo de tempo Δt.
b. o período do movimento no plano perpendicular a B.
c. a trajetória seguida pelo elétron, graficamente.
Resolução:
Dados:
massa do elétron: m
Carga: - e
Velocidade: v
a) τ = 0, pois a força magnética ( FM ) é sempre perpendicular ao vetor velocidade.
b) Na figura, decompondo o vetor v em v, e v, temos, independentemente, um MRU em z e um MCU no plano xOy. Precisamos calcular o
período desse último movimento:
No MCU, a FM é uma força centrípeta:
FM = Fcp
q ⋅ vy ⋅ B =
m ⋅ vy
m ⋅ v ⋅2
∴ R=
R
q⋅B
A partir de R:
ΔS
2π ⋅ R
∴ vy =
Δt
T
2π ⋅ R 2π ⋅ m ⋅ v y
2π ⋅ m
T=
=
∴ T=
vy
vy ⋅ q ⋅ B
q⋅B
v=
Substituindo q por e:
T=
2π ⋅ m
e⋅B
c)
2
Questão 03
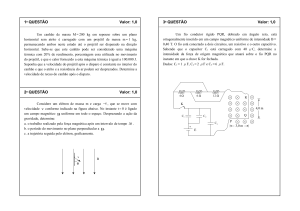
Um fio condutor rígido PQR, dobrado em ângulo reto, está
ortogonalmente inserido em um campo magnético uniforme de
intensidade B = 0,40 T. O fio está conectado a dois circuitos, um
resistivo e outro capacitivo. Sabendo que o capacitor C1 está
carregado com 40 μC, determine a intensidade da força de origem
magnética que atuará sobre o fio PQR no instante em que a chave
K for fechada.
Dados: C1 = 1 μF, C1 = 2 μ F e C1 = 6 μ F
Resolução:
Simplificando o circuito capacitivo, temos:
ε = VAB + VCB
Para o cálculo de VAB, temos:
C1 =
40μ
40μ
∴ VAB =
VAB
1μ
VAB = 40 V
Daí, temos que em C2 em paralelo:
Q2 = VAB. C2 = 80 μC
Para o cálculo de VCB devemos observar que o sistema isolado na figura está neutro. Assim:
Q1 + Q2 = Q3
∴
Q3 = 120 μC
E logo:
VBC =
Q3 120μ
=
= 20V
C3
6μ
Fechada a chave K, o circuito e o fio PQR ficam em série e sujeitos à voltagem total VCB = 20 V, sendo que não foi fornecida a resistência PQR,
que será desprezada.
Simplificando o elemento resistivo:
1
1 1 1
= + +
Req 4 6 12
1
3 + 2 +1
=
∴ Req = 2Ω
Req
12
De onde agora obtemos a corrente que circula em PQR:
i=
VBC 20V
=
= 10 A
Req
2Ω
Calculando agora as forças que atuam nos segmentos RQ
e PQ separadamente e em direções perpendiculares,
encontramos:
FRQ = BiLRQ = 0, 4 ⋅ 10 ⋅ 4 = 16 N
FPQ = BiLPQ = 0, 4 ⋅ 10 ⋅ 3 = 12 N
Dando uma resultante R, tal que:
R 2 = FPQ 2 + FRQ 2 ⇒ R = 20N
3
Questão 04
Uma corda é fixada a um suporte e tensionada por uma esfera totalmente
imersa em um recipiente com água, como mostra a figura. Desprezando o
volume e a massa da corda em comparação com o volume e a massa da
esfera, determine a velocidade com que se propaga uma onda na corda.
Dados: aceleração da gravidade (g) = 10 m/s2;
densidade linear da corda (μ) = 1,6 g/m;
massa da esfera (m) = 500 g;
volume da esfera (V) = 0,1 dm3
massa específica da água (d) = 1000 kg/m3
Resolução:
Para a esfera em equilíbrio podemos escrever:
T+E=P
T = P – E = m.g – d.g.Ve
T = 0,5 ⋅ 10 − 103 ⋅ 10 ⋅ (10−4 ) ∴ T = 4 N .
Cálculo da velocidade de propagação da onda na corda:
v=
T
μ
=
4
102
=
= 50m / s
−4
16 ⋅ 10
2
Questão 05
Um corpo de massa m e volume v = 1 m3, imerso em um líquido de massa
específica ρ0 é solto, inicia um movimento vertical, atinge o anteparo A e
provoca uma deformação máxima x na mola de constante elástica K. Em
seguida, o procedimento é repetido, porém com líquido de massa
específica ρ1 diferente de ρ0. O gráfico abaixo mostra a relação entre a
variação da massa específica do líquido Δρ e variação da deformação
máxima da mola Δx.
a. Construa o gráfico da deformação máxima da mola x em função da
diferença entre as massas específicas do corpo e do líquido ΔρCL.
b. Determine o valor de x para ΔρCL = 1000 kg/m3.
Dado: aceleração da gravidade (g) = 10 m/s2.
Resolução:
Da conservação da energia.
Para o líquido de massa específica ρ0:
ρCV ⋅ g ⋅ h = ρ0 ⋅ V ⋅ g ⋅ h +
Kx 2
2(ρc − ρ0 )Vgh
⇒ x2 =
2
k
I
Para o líquido de massa específica ρ1:
4
ρcVgh = ρ1Vgh +
Kx12
⇒
2
K ⋅ ( x + Δx) 2
⇒
2
2(ρc − ρ0 )Vgh 2ΔρVgh
−
= x 2 + 2 xΔx + (Δx) 2
k
k
ρcVgh = (ρ0 + Δρ)Vgh +
II
De I e II, lembrando que Δx é pequeno ((Δx) 2 → 0) e considerando as deformações em módulo no gráfico dado, vem:
ΔρVgh
500 ⋅ 1 ⋅ 10 ⋅ h
h
x
= xΔx ⇒
= x ⋅ 0,01 ∴ =
K
K
k 5.105
a) Do que já foi exposto vem:
ρcVgh = ρ LVgh +
Kx 2
2
Vgh.2
= x2
K
x
ΔρcL ⋅ 1 ⋅ 10 ⋅ 2 ⋅
= x2
5.105
∴ x = 4 ⋅ 10−5 ⋅ ΔρcL
(ρc − ρ L ) ⋅
Obs.: Caso não fosse feito aproximação (Δx)2 ≅ 0 o gráfico acima seria um arco de parábola.
b) Do item anterior:
x = 4 · 10-5 · 1000 m
∴
x = 4 · 10-2 m.
Questão 06
Determine a ordenada d de um ponto P, localizado sobre a lente
convergente de distância focal 6 cm, no qual deve ser mirado um
feixe laser disparado do ponto A, com o intuito de sensibilizar um
sensor ótico localizado no ponto B. Considere válidas
as
aproximações de Gauss.
Resolução:
Relações encontradas na figura:
I) ΔOMA ' ∼ ΔONB '
x y
=
4 10
II)
x = 1,0 − d
III) ΔVPO ∼ ΔVBB '
d 2, 4 − y
=
= 4d = 6.2, 4 − 6 y
6
4
5
6 y = 2, 4.6 − 4d
y = 2, 4 − 2 d
3
Substituindo II e III em I:
1,0 − d
=
4
2
2, 4 − d
3
10
8
−10d + 10 = 9,6 − d
3
22
d = 0, 4
3
1, 2
d=
= 0,054545...
22
d ≅ 0,055 cm ≅ 5,5.10−2 cm
Questão 07
Um gás ideal encontra-se, inicialmente, sob pressão de 1,0
atmosfera e ocupa um volume de 1,0 litro em um cilindro de raio
R = 5/π m, cujo êmbolo mantém a placa P2 de um capacitor
afastada 10 cm da placa paralela P1. Nessa situação, existe uma
energia de 171,5μJ armazenada no capacitor, havendo entre suas
placas a tensão de 5,0 V. Determine o valor da capacitância
quando o êmbolo for levantado, reduzindo a pressão
isotermicamente para 0,8 atm.
Resolução:
Condições iniciais do capacitor:
E=
2 ⋅ E 2 ⋅ 171,5 ⋅ 10−6
CU 2
⇒C = 2 =
F ⇒∴ C = 13,72 ⋅ 10−6 F
2
52
U
d = 10cm (distância entre as placas)
Analise do gás:
PV
PV
1 1
= 2 2 ⇒ 1 ⋅ 1 = 0,8V2 ⇒ V2 = 1, 25 L
T1
T2
Cálculo da variação da altura da altura do embalo:
πR 2 ⋅ Δh = ΔV
0, 25L
25 ⋅ 10−5 m3
ΔV
=
=
= π ⋅ 10−5 m
2
25
25 2
πR
π ⋅ 2 m2
⋅m
π
π
Δh = 3,14 ⋅ 10−5 m = 3,14 ⋅ 10−3 cm
Δh =
Essa variação de altura diminui a distância entre as placas do capacitor para (10 - 0,003) cm = 9,997 cm
Seja C’ a nova capacitância:
6
A ⎫
dC
10 ⋅ 13,72 ⋅ 10−6
d ⎪⎪ C ' d
∴ C' =
F = 13,72 ⋅ 10−6 F
= ⇒ C'=
⎬
A ⎪ C d'
d'
9,997
C' =ε
d ' ⎪⎭
Levando em consideração a quantidade de algarismos significativos nos dados da questão concluímos que C ' = C = 14μF , ou seja, sua
variação não é significativa.
C =ε
o
o
Questão 08
A Figura 1 mostra um cilindro de raio R = 0,2 m em repouso e um
bloco de massa m = 0,1 kg, suspenso por uma mola de constante
elástica k. Junto ao bloco existe um dispositivo que permite registrar
sua posição no cilindro. Em um determinado instante, o bloco é
puxado para baixo e solto. Nesse mesmo instante, o cilindro começa
a girar com aceleração angular constante γ = 0,8 rad/s2 de tal
maneira que a posição do bloco é registrada no cilindro conforme a
Figura 2. Determine:
a) o período T de oscilação do bloco em segundos;
b) o valor da constante elástica k da mola em N/m;
c) a deformação da mola em metros antes de o bloco ter sido
puxado;
d) a amplitude total em metros do movimento de oscilação,
apresentado no gráfico da Figura 2, sabendo que a energia
potencial elástica máxima do conjunto bloco – mola é de 2,0 J.
Dados: aceleração da gravidade (g) = 10 m/s2;
π2 ≅ 10
Resolução:
a) Em x, a rotação do cilindro durante um ciclo completo cria um deslocamento Δx = 2 ⋅ 10−2 m , e como temos um MUV:
at 2
(sendo a= γ ⋅ R = 16 ⋅ 10−2 m 2 )
s
2
−2
2
16 ⋅ 10 ⋅ t
2 ⋅ 10−2 =
2
t = 0,5 s
Δx =
b) T = 2π
m
k
1
10−1
= 2π
2
k
k = 10−1 ⋅ 16 ⋅ π2 (em que π2 ≅ 10 )
k = 1,6.10 k = 16 N
m
c) Na situação inicial de repouso, podemos fazer
Fr = 0 , e logo
P = Fel
Mg = kx0
x0 =
1
m = 0,063 m
16
7
d) Quando a energia potencial elástica é máxima, a elongação da mola vale x = x0 + A . Sendo X 0 a deformação inicial que equilibrava a
força peso:
k ( x0 + A) 2
=2
2
k ( x0 + A) 2 = 4
Epmol =
( x0 + A) 2 = 1
4
g x ⋅ m = 402 ⋅ 10−2
g x ⋅ 1,005 = 402 ⋅ 10−2
g x = 4 m/s 2
A = 0, 4375 m
Resposta: A ≅ 0, 44 m
Questão 09
Um objeto foi achado por uma sonda espacial durante a exploração de um planeta distante. Esta sonda possui um braço ligado a uma mola
ideal presa a garras especiais. Ainda naquele planeta, observou-se no equilíbrio um deslocamento xP = 0,8 ⋅ 10−2 m na mola, com o objeto
totalmente suspenso. Retornando à Terra, repetiu-se o experimento observando um deslocamento xT = 2,0 ⋅ 10−2 m . Ambos os deslocamentos
estavam na faixa linear da mola.
Esse objeto foi colocado em um recipiente termicamente isolado a 378 K em estado sólido. Acrescentou-se 200 g de gelo a 14 °F. Usando um
termômetro especial, graduado em uma escala E de temperatura, observou-se que o equilíbrio ocorreu a 1,5 °E , sob pressão normal.
Determine:
a) a razão entre o raio do planeta de origem e o raio da Terra;
b) o calor específico do objeto na fase sólida.
Dados: a massa do planeta é 10% da massa da terra;
aceleração da gravidade na Terra (g) = 10 m/s2;
temperatura de fusão da água sob pressão normal na escala E: -12°E;
temperatura de ebulição da água sob pressão normal na escala E: 78 °E;
calor especifico do gelo: 0,55cal/g°C;
calor especifico da água na fase líquida: 1,00 cal/g°C;
calor latente de fusão da água: 80 g/cm3;
massa especifica da água: 1 g/cm3;
constante elástica da mola (k) = 502,5 N/m.
Resolução:
a) Enquanto o objeto está suspenso, a força resultante sobre ele é nula, ou seja, Fel = P :
Então, como Fel = k ⋅ x , temos para ambos planetas:
No planeta distante (X): k ⋅ xx = m ⋅ g x
Na Terra: k ⋅ xT = m ⋅ gT
⇒
⇒
k ⋅ 0,8 ⋅ 10−2 = m ⋅ g x (1)
k ⋅ 2,0 ⋅ 10−2 = m ⋅ gT (2)
E, dividindo-se (1) por (2) obtemos:
g x 0,8 2
=
=
gT 2,0 5
E, lembrando que o campo gravitacional na superfície do é dado por g =
G⋅M
,e que, a massa do planeta é 10% da massa da terra,
R2
obtemos:
gx
=
gT
G ( M x ⋅ 0,1)
Rx 2
2
=
GM T
5
RT 2
8
2
⇒
⎛ RT ⎞
20
=4
⎜ ⎟ =
R
5
⎝ x⎠
Logo,
Rx 1
=
RT 2
b) Primeiro vamos estabelecer uma equação de conversão entre as escalas 0E e 0F:
(1)
gelo
m
c ou L
θ−0
θ + 12
= Ε
100 − 0 78 + 12
⇒
200 g
c=0,55
cal/g0C
(2)
fusão do
gelo
200 g
(3)
(4)
água fundida
objeto
200 g
1005 g
L=80 cal/g
c=1 cal/g C
c
378 K = 105
0
C
15 0C
Ti
-10 0C
-
0oC
Tf
0
-
15 0C
θ
θ + 12
= Ε
100
90
10 ⋅ θΕ + 120 = 9 ⋅ θC
Cálculo da temperatura de equilíbrio
9 ⋅ θº C = 10 ⋅ 1,5 + 120
9 ⋅ θº C = 10 ⋅ 1,5 + 120
θ0C = 15 0C
Temperatura do gelo na escala Celsius:
(θ − 32)
θC = F
⋅5
9
5
θC = (14 − 32) ⋅
9
θC = −10 0C
Temperatura do objeto:
θ = 378 K = 105 0C
Calores trocados
- objeto
0
Q1 = m1 ⋅ c1 ⋅ Δθ1 = 1,005 ⋅ c ⋅ (15 − 105)
Q1 = −90450 ⋅ c
- gelo (aquecimento até 0ºC)
Q2 = m ⋅ c ⋅ Δθ2 = 200 ⋅ 0,05 ⋅ (0 + 10)
Q2 = 1100 cal
- gelo (fusão)
Q3 = m ⋅ L = 200 ⋅ 80 = 16000 cal
- aquecimento da água fundida Q4 = m ⋅ c ⋅ Δθ3 = 200 ⋅ 1 ⋅ (15 − 0 ) ou Δθ4 = 3000
∑Q = 0
−90450 ⋅ c + 1100 + 16000 + 3000 = 0
2
c ≅ 0, 22 cal 0 = cal 0
g C q
g C
9
Questão 10
Um feixe de luz monocromática incide perpendicularmente aos planos da fenda retangular e do anteparo, como mostra a figura. A fenda
retangular de largura inicial a é formada por duas lâminas paralelas de baquelite, fixadas em dois tubos de teflon, que sofrem dilatação linear
na direção de seus comprimentos. Estes tubos envolvem dois filamentos de tungstênio, que estão ligados, em paralelo, a uma fonte de 1,5 V.
Após o fechamento da chave S, uma corrente i = 500 mA atravessa cada tubo de teflon fazendo com que a figura de difração, projetada no
anteparo, comece a se contrair. Considerando que a energia dissipada no filamento de tungstênio seja totalmente transmitida para o tubo de
teflon, determine o tempo necessário para que o segundo mínimo de difração ocupe a posição onde se encontrava o primeiro mínimo.
Dados : calor específico do teflon = 1050 J/kg · k;
coeficiente de dilatação linear do teflon = 216x10-6 °C-1;
massa do tubo de teflon = 10 g;
comprimento inicial da barra de teflon (L0) = 10a, onde “a” é a largura inicial da fenda.
Resolução:
Em uma fenda simples, os mínimos de difração são calculados da forma:
a ⋅ senθ = m ⋅ λ , com m = 1,2,3,...
Logo, para que o segundo mínimo (m = 2) passe a ocupar a posição onde se encontrava o primeiro mínimo (m = 1), ou seja, para que θ não
varie, a abertura a da fenda deve dobrar.
a ⋅ senθ = (1) ⋅ λ
a′ ⋅ senθ = (2) ⋅ λ ⇒ a′ = (2) ⋅ a
Daí o comprimento L0 do tubo de teflon também deve dobrar, ou seja
ΔL = L0
L0 ⋅ α ⋅ Δθ = L0
⇒
Δθ =
1
1
=
ºC
α 216 ⋅ 10−6
Cálculo do tempo gasto para a dilatação:
Q = m ⋅ c ⋅ Δθ
P ⋅ Δt = m ⋅ c ⋅ Δθ
1
º C)
216 ⋅ 10−6
1
m⋅c⋅(
º C)
⋅ 10−6
216
Δt =
U ⋅i
10 ⋅ 10−3 ⋅ 1050 ⎛
1
⎞
Δt =
⋅⎜
⎟s
(1,5 ⋅ 500 ⋅ 10−3 ) ⎝ 216.10−6 ⎠
(U ⋅ i ) ⋅ Δt = m ⋅ c ⋅ (
Δt = 6,5 ⋅ 104 s
10
Comentários
O IME manteve sua tradição. A prova possui conteúdos distribuídos de forma homogênea, com questões em dois níveis: médio e difícil. Uma
prova em que o candidato tem que demonstrar suas habilidades com os cálculos e a capacidade de inter-relacionar conteúdos diferentes. A
prova é longa, como de costume, em que o candidato deve selecionar as questões que ele faz em pouco tempo, deixando as maiores e de
mesmo peso, para o final. Todo o conteúdo cobrado nelas foi trabalhado em sala com nossos alunos, de forma que só coube a eles a
organização dos dados e dissertação e/ou escolha do caminho correto.
Incidência de assuntos:
Física Moderna
0%
Eletricidade
30%
Cinem ática
14%
Dinâm ica
14%
Ondas
7%
Óptica
7%
Hidros tática/Estática
14%
Term ologia
14%
Professores :
Bernadelli
Marcelo Moraes
Colaboradores:
Manfredo
Rodrigo Lacerda
Frederico Furst
Digitação e Diagramação
Diego Bernadelli
Projeto Gráfico
Frederico Bueno
Assistente Editorial
Diego Bernadelli
Supervisão Editorial
Rodrigo Bernadelli
Copyright©Olimpo2004
11