Document

Lista de Exercícios1
Rotações.
Autores: Momotaro Imaizumi
Carlos Alberto Soufen
Carlos Alberto Fonzar Pintão.
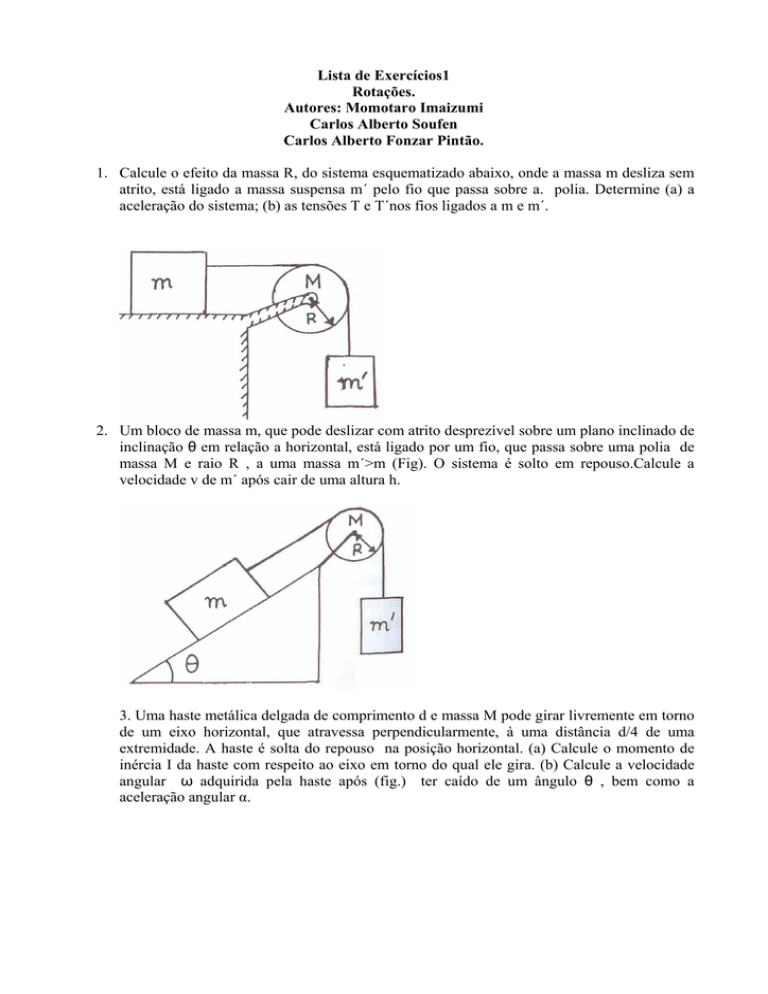
1. Calcule o efeito da massa R, do sistema esquematizado abaixo, onde a massa m desliza sem
atrito, está ligado a massa suspensa m´ pelo fio que passa sobre a. polia. Determine (a) a
aceleração do sistema; (b) as tensões T e T´nos fios ligados a m e m´.
2. Um bloco de massa m, que pode deslizar com atrito desprezível sobre um plano inclinado de
inclinação θ em relação a horizontal, está ligado por um fio, que passa sobre uma polia de
massa M e raio R , a uma massa m´>m (Fig). O sistema é solto em repouso.Calcule a
velocidade v de m´ após cair de uma altura h.
3. Uma haste metálica delgada de comprimento d e massa M pode girar livremente em torno
de um eixo horizontal, que atravessa perpendicularmente, à uma distância d/4 de uma
extremidade. A haste é solta do repouso na posição horizontal. (a) Calcule o momento de
inércia I da haste com respeito ao eixo em torno do qual ele gira. (b) Calcule a velocidade
angular ω adquirida pela haste após (fig.) ter caído de um ângulo θ , bem como a
aceleração angular α.
4.Uma roda cilíndrica, de raio R e massa M , rola sem deslizar sobre um plano horizontal ,
deslocando se com velocidade v e sobe um plano inclinado de inclinação θ, continuando a
rolar sem deslizamento(fig.) Até que altura h o centro da roda subirá sobre o plano
inclinado.
5. Uma bola de boliche esférica uniforme é lançada com velocidade inicial
r
v 0 horizontal e sem rotação inicial sobre uma concha horizontal, com coeficiente de atrti=o
cinético μc . (a) Que distância d a bola percorrerá percorrera sobre a prancha até que comece
a rolar sem deslizar. (b) Quanto tempo t depois do lançamento isso ocorre? (c) Qual é a
velocidade v da bola nesse instante.
6. Duas partículas de massa m estão presas ás extremidades de uma molade massa
desprezível , inicialmente com seus comprimentos l0 > A mola é esticada até o dobro desse
comprimento e é solta depois de comunicar velocidades iguais e opostas (v0 , -v0) as
partículas, perpendiculares à direção da mola. (fig.), tais que kl02 = 6mv02 , onde k é a
constante de mola. Calcule a componentes (vr , vθ ) radial e transverasl da partículas quando
a mola volta a passar pelo comprimento relaxado.
7. No sistema da figura, análogo a um regulador centrífugo , o anel A, de massa desprezível
, pode deslizar ao longo do eixo vertical. Inicialmente, as duas bolas iguais de massa
m=200gestão a uma distância r=15 cm do eixo e o sistema gira com velocidade angular
ω=6rad/s. Pressiona-se para baixo o anel A, até que a distância das bolas ao eixo aumenta
para r=25 cm.(a) Qual é a sua nova velocidade angular de rotação. (b) Qual é o trabalho
realizado sobre o sistema.