Be Ae tx

Física 2 – Atividade 3 -Rotação de corpos rígidos e Dinâmica do Movimento de Rotação - MHS
Torque e Momento Angular - Prof. Dr. Cláudio Sérgio Sartori
2
m
m  r2
3

d


d


I

o
0
  r 2 0
2
r
Io 
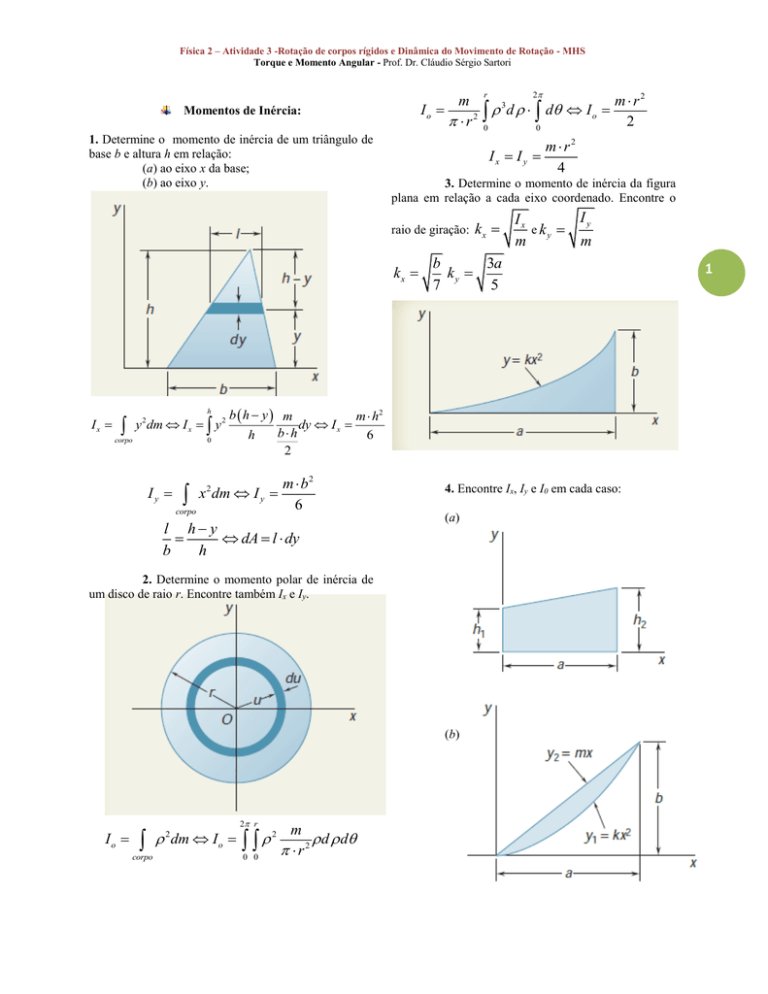
Momentos de Inércia:
1. Determine o momento de inércia de um triângulo de
base b e altura h em relação:
(a) ao eixo x da base;
(b) ao eixo y.
m  r2
Ix  I y 
4
3. Determine o momento de inércia da figura
plana em relação a cada eixo coordenado. Encontre o
raio de giração:
kx 
Ix 
h

y 2 dm  I x   y 2
corpo
0
Iy 

x 2 dm  I y 
m  b2
6
l h y

 dA  l  dy
b
h
3a
b
ky 
5
7
4. Encontre Ix, Iy e I0 em cada caso:
(a)
2. Determine o momento polar de inércia de
um disco de raio r. Encontre também Ix e Iy.
(b)
Io 

corpo
Iy
Ix
e ky 
m
m
bh  y m
m  h2
dy  I x 
bh
h
6
2
corpo
 dm  I o 
2
kx 
2 r
 
0 0
2
m
 d  d
  r2
1
Física 2 – Atividade 3 -Rotação de corpos rígidos e Dinâmica do Movimento de Rotação - MHS
Torque e Momento Angular - Prof. Dr. Cláudio Sérgio Sartori
5. Determine o momento polar de inércia IO e
o raio de giração da figura plana com respeito ao centro
P.
8. Encontre o momento de inércia da figura
composta com respeito ao eixo x.
2
6. Determine o momento polar de inércia IO e
o raio de giração da figura plana com respeito ao centro
O.
9. Determine o momento de inércia com
respeito à um eixo perpendicular à extremidade de uma
barra de massa m e comprimento L.
7. Aplique o teorema dos eixos paralelos ou
teorema de Steiner:
IO  IG  m  OG
2
para encontrar o momento de inércia em relação aos
eixos indicados:
(a)
10. Encontre o momento de inércia das
figuras (triângulo equilátero de lado a) e massa m em
relação ao eixo CC’. (passando pelo centro de massa
G=C).
(a)
(b)
(b)
.
Física 2 – Atividade 3 -Rotação de corpos rígidos e Dinâmica do Movimento de Rotação - MHS
Torque e Momento Angular - Prof. Dr. Cláudio Sérgio Sartori
rampa em relação à horizontal é . Qual é a aceleração
da bola? Considere a bola uma esfera homogênea
sólida, desprezando seus orifícios.
Torque e momento angular. Energia de rotação.
1. Uma casca cilíndrica oca de raio R e massa
M rola sem deslizar com uma velocidade vCM ao longo
de uma superfície plana. Qual a sua energia cinética?
Dado:
K
1
1
2
M  vcm
 I cm   2
2
2
2. Velocidade de um ioiô. Um ioiô é feito
enrolando-se um fio diversas vezes em torno de um
cilindro de massa M e raio R. Mantém-se presa a
extremidade enquanto o cilindro é liberado sem
velocidade inicial. O fio se desenrola, mas não desliza
nem se dilata à medida que o cilindro cai e gira. Use
considerações de energia para achar a velocidade do
centro de massa vCM do cilindro sólido depois que ele
caiu a uma distância h.
3
5. Trabalho e potência no movimento de
rotação. Podemos escrever:
dW  Ftan ds  ds  R  d
dW  Ftan  R  d  dW    d 
2
W     d  dW    d
1
dW  I    d  dW  I 
d
 d
dt
d
 d  dW  I   d
dt
2
1
1
W   I    d  Wtot  I  22  I  12
2
2
1
dW  I 
3. Competição entre corpos girando. Em uma
demosntração durante a aula de física, o professor faz
uma “competição” de vários corpos rígidos redondos:
cicllindro oco, cilindro sólido, aro, esfera oca e esfera
sólida. Deixando-os rolar do alto de um plano inclinado,
qual a forma do corpo que alcança primeiro a parte
inferior ?
dW
d
 
 P   
dt
dt
Um anúncio fazendo propaganda da potência
desenvolvida pelo motor de um automóvel afirma que o
motor desenvolve 1.49.105W para uma rotação de 6000
rpm. Qual é o torque desenvolvido pelo motor?
6. A hélice da turbina de um motor a jato possui
momento de inércia 2.5 kg.m² em torno do eixo de
rotação. Quando a turbina começa a girar, sua
velocidade angular em função do tempo é dada por
  400  t 2 rad s3 
Dados: Conservação da energia mecânica:
K1  U1  K2  U2
Dica:
Icm  c  M  R2
Veja tabela.
4. Aceleração de uma esfera rolando. Uma esfera
de bliche sólida rola sem deslizar para baixo de uma
rampa ao longo de uma guia. O ângulo de inclinação da
(a) Calcule o momento angular da hélice em função
do tempo e ache seu valor em t = 3.0 s.
(b) Determine o torque resultante que atua sobre a
hélice em função do tempo e calcule seu valor para t =
3.0 s.
Física 2 – Atividade 3 -Rotação de corpos rígidos e Dinâmica do Movimento de Rotação - MHS
Torque e Momento Angular - Prof. Dr. Cláudio Sérgio Sartori
7. Uma grandeza análoga ao momento linear p de
uma partícula é o momento angular, que representamos
por L . Definimos como: L  r  p
10. Qualquer um pode ser bailarino. Um professor
de física acrobata está de pé sobre o centro de uma mesa
girante,
mantendo
seus
braços
estendidos
horizontalmente com um haltere de 5.0 kg em cada
mão.
4
Se um corpo de 2 kg possui vetor posição dado por:
r  2  iˆ  3  ˆj  5  kˆ  m
E vetor velocidade:
v  3  iˆ  4  ˆj  2  kˆ  m s 
Determine seu momento angula L .
8. Uma pedra de 2.00 kg possui uma
velocidade horizontal com modulo de 12.0 m/s quando
esta no ponto P na Figura. (a) Nesse instante, qual é o
modulo, a direção e o sentido do seu momento angular
em relação ao ponto O ? (b) Caso a única força que
atue sobre a pedra seja seu peso, qual é a taxa de
variação (módulo, direção e sentido) do momento
angular nesse instante ?
9. Um patinador girando. Podemos
considerar as mãos e os braços esticados para fora de
um patinador que se prepara para girar como uma barra
delgada cujo eixo de giro passa pelo seu centro de
gravidade (Figura 14). Quando suas mãos e braços se
aproximam do corpo e se cruzam em torno do corpo
para executar o giro, as mãos e os braços podem ser
considerados um cilindro oco com parede fina. A massa
total das mãos e dos braços e igual a 8.0 kg. Quando
esticadas para tora, a envergadura é de 1.8 m; quando
torcidas, elas formam um cilindro de raio igual a 25 cm.
O momento de inércia das parles restantes do corpo em
relação ao eixo de rotação é constante e igual a 0,40 kg
m². Se sua velocidade angular inicial é de 0,40 rev/s,
qual é sua velocidade angular final ?
Ele está girando em torno de um eixo vertical
completando uma volta a cada 2.0 s. Calcule a nova
velocidade angular do professor quando ele aproxima os
dois halteres do seu estômago e discuta como isso
modifica a sua energia cinética. Seu momento de
inércia (sem os halteres) é igual a 3.0 kg.m² quando seus
braços estão distendidos para fora, diminuindo para 2.2
kg.m² quando suas mãos estão próximas do seu
estômago. Os halteres estão inicialmente a uma
distância de 1.0 m do eixo e a distância final é igual a
0.20 m. Considere o halteres como partículas.
11. A figura mostra 2 discos, um deles é o volante
de um motor e o outro é um disco ligado a um eixo de
transmissão. Seus momentos de inércia são IA e IB,
respectivamente; inicialmente eles estão girando com a
mesma velocidade angular A e B, respectivamente. A
seguir empurramos os dois discos um contra o outro
aplicando forças que atuam ao longo do eixo, de modo
que sobre nenhum dos dois discos surge torque em
relação ao eixo. Os discos permanecem unidos um
contra o outro e atingem uma velocidade angular final
. Deduza uma expressão para .
Física 2 – Atividade 3 -Rotação de corpos rígidos e Dinâmica do Movimento de Rotação - MHS
Torque e Momento Angular - Prof. Dr. Cláudio Sérgio Sartori
12. No exemplo anterior, suponha que o volante
A tenha massa de 2.0 kg, um raio de 0.20 m e uma
velocidade angular inicial de 200 rad/s. Calcule a
velocidade angular comum final  depois que os discos
ficam em contato. A energia cinética se conserva nesse
processo?
13. Momento angular em uma ação policial.
Uma porta de largura 1 m e massa de 15 kg é articulada
com dobradiças em um dos lados de modo que possa
girar sem atrito em torno de um eixo vertical. Ela
inicialmente não está aberta. Um policial dá um tiro
com uma bala de 10 g e velocidade de 400 m/s
exatamente no canto da porta. Calcule a velocidade
angular da porta imediatamente depois que a bala
penetra na porta. A energia cinética se conserva?
14. Determinar, em cada caso, o momento angular
para as seguintes situações:
(a) um carro de 1200 kg percorre no sentido
anti-horário um círculo com 20 m de raio com
velocidade de 15 m/s.
(b) o carro mencionado desloca-se com
velocidade
v  15  m s   iˆ sobre a reta y = y0 =20m,
paralela ao eixo x.
(c) um disco, no plano xy, com raio de 20 m e a
massa de 1200 kg, girando a 0.75 rad/s em torno do seu
eixo, que coincide com o eixo z.
15. A máquina de Atwood tem dois corpos de
massa m1 e m2 ( sendo m1 maior que m2), ligados por um
cordel de massa desprezível que passa por uma polia
cujos rolamentos não oferecem atrito. A polia é um
disco uniforme, de massa M e raio R. O cordel não
escorrega na polia. Determinar a aceleração angular da
polia e a aceleração dos dois corpos pela equação:
N

i 1
i ,ext

dL
dt
5
16. Um disco gira em torno de um eixo sem atrito,
que coincide com o respectivo eixo de simetria, com
velocidade angular inicial i, como mostra a figura. O
seu momento de inércia em relação ao eixo é I1. Num
certo instante, o disco cai sobre o outro, de momento de
inércia I2, montado sobre o mesmo eixo. Graças ao
atrito entre as duas superfícies em contato, os dois
discos atingem uma velocidade angular comum aos
dois, f. Calcular essa velocidade angular.
17. Um carrossel com 2 m de raio e 500 kg.m2 de
momento de inércia gira em torno de seu eixo, sem
atrito, completando uma volta a cada 5 s. Uma criança,
com 25 kg, está inicialmente no centro do carrossel e
depois caminha até a borda. Calcular a velocidade
angular que terá, então, o carrossel.
18.
A criança mencionada no exemplo anterior
corre com velocidade 2.5 m/s sobre uma tangente à
beira da plataforma do carrossel, que está imóvel, e pula
para a plataforma. Calcular a velocidade angular final
da criança no carrossel.
Física 2 – Atividade 3 -Rotação de corpos rígidos e Dinâmica do Movimento de Rotação - MHS
Torque e Momento Angular - Prof. Dr. Cláudio Sérgio Sartori
19.
Uma partícula de massa m descreve, com
velocidade v0, um círculo de raio r0 sobre a superfície de
uma mesa horizontal sem atrito. A partícula está presa a
um fio que passa por um buraco na mesa, no centro do
círculo. O fio é lentamente puxado para baixo, de modo
que a partícula acaba descrevendo um círculo de raio rf.

Momento de inércia de figuras:
6
(a) Calcular a velocidade final em termos de r0, v0 e
rf.
(b) Calcular a tensão T no fio quando a partícula
descreve um círculo de raio rf em termos de m, r e do
momento angular L0  m  v0  r0 .
(c) Calcule o trabalho feito pela partícula pela tensão
T, integrando T  dr de r0 até rf. Dar a resposta em
termos de r0, rf e L0.
20. Uma barra de massa M e comprimento d pode
girar em torno de um eixo fixo a uma de suas
extremidades. Uma bola de massa plástica, com massa
m e velocidade v, atinge a barra a uma distância x do
eixo e fica grudada na barra.
Achar a razão entre a energia final e a energia inicial
do sistema.
Física 2 – Atividade 3 -Rotação de corpos rígidos e Dinâmica do Movimento de Rotação - MHS
Torque e Momento Angular - Prof. Dr. Cláudio Sérgio Sartori
Lista e Trabalho:
1. Aplica-se uma força de 18 N a uma distância
rs = 7 cm do eixo central da catraca traseira de uma
bicicleta. Considere a roda de momento de inércia I =
M.R2 de raio R = 35 cm e massa M = 2.4 kg. Qual a
velocidade angular da roda após 5 s?
O bloco de massa m1 desliza sem atrito sobre uma
superfície horizontal; o bloco de massa m2 está
suspenso. Encontre a aceleração dos blocos e as tensões
T1 e T2 assumindo que a corda não desliza sobre a polia.
R: a 
2. Uma haste de comprimento L e massa M está
pivotada em sua extremidade esquerda. O engaste está
ausente de atrito. Encontre: (a) a aceleração angular
imediatamente a haste ser solta e (b) a força FA exercida
no pivô nesse instante.
m2
m1  m2 
I
g  T1 
R2
m2
m1  m2 
I
R2
m1  g  T2 
m1 
I
R2
m1  m2 
I
m2  g
R2
5. O máximo torque produzido por um motor
8.0-L V10 de um Dodge Viper 2002 é 675 N.m a 3700
rev/min. Encontre a potência desse carro operando nas
condições de máximo torque. (R: 262 kW).
6. A máxima potência produzida por um Dodge
Viper é 450 hp a 5200 ver/min. Qual é o torque do
motor quando operando na máxima potência?
(R: 616 N.m)
7. Uma bola de raio 11 cm e massa M = 7.2 kg
está rolando sem se deslizar sobre um plano horizontal
com velocidade de 2 m/s. Se ela sobre o plano inclinado
sem se deslizar e para a uma altura h, determine a altura
h atingida.
R:
  32gL  FA  14 Mg
3. Um objeto de massa m está ligado por um fio
a uma polia que possui momento de inércia I e raio R. O
fio se movimenta sem se deslizar pela polia e não há
atrito. Encontre a tensão no fio e a aceleração do objeto.
R: h 
7  vi2
10  g
8. Um taco atinge horizontalmente uma esfera
a uma distância x de seu centro. Encontre o valor de x
para o qual a bola vai rolar sem se deslizar. Expresse
sua resposta em termos do raio R da bola.
R:
T
m g
g
a
2
I
m R
1
1
m  R2
I
4. Dois blocos são conectados por uma corda e
passam por uma polia de raio R e momento de inércia I.
7
Física 2 – Atividade 3 -Rotação de corpos rígidos e Dinâmica do Movimento de Rotação - MHS
Torque e Momento Angular - Prof. Dr. Cláudio Sérgio Sartori
R: x 
2 R
5
9. Uma bola sólida de massa m e raio R rola
sem deslizar-se sobre um plano inclinado de um ângulo
 com a horizontal. Determine a aceleração do centro de
massa e a força de atrito.
R: acm  5 g  sen  Fat  2 m  g  sen
7
7
10. Uma esfera sólida, um cilindro sólido e um
aro são abandonados de uma altura h de um plano
inclinado. Determine a velocidade com que chegam ao
solo. (para cada objeto).
11. Uma máquina de Atwood possui duas
massas m1 = 500 g e m2 = 510 g conectadas por uma
corda de massa desprezível que passa por uma polia
(um disco uniforme de massa 50 g e raio 4 cm). A corda
não se desliza sobre a polia. Encontre a aceleração dos
objetos e as tensões que suportam as massas,
13. Encontre o momento angular L  r  p na
origem de um carro de massa m = 1200 kg que se move
em um círculo de raio 20 m com velocidade de 15 m/s.
O círculo está no plano xy, centrado na origem. Quando
visto de um ponto no eixo z o carro se move no sentido
anti-horário.
14. Um disco está girando com velocidade
angular inicial i em um sistema sem atrito sobre um
eixo de simetria. O momento de inércia em relação a
esse eixo é I1. Ela cai sobre um outro disco de momento
de inércia I2 que está inicialmente em repouso sobre o
mesmo eixo. Devido ao atrito, elas giram juntos.
Determine a velocidade angular comum dos dois discos.
(Aplicação: Os discos girando no eixo de
transmissão de um caminhão fazem colisões
inelásticas.)
12. Uma máquina de Atwood possui duas
massas m1 e m2 (m1 > m2) conectadas por um fio. A
polia é um disco uniforme de massa M e raio R. O fio
não desliza sobre a polia. Aplique a relação:

i
i

dL
para o sistema constituído pelos dois
dt
blocos, a polia e o fio para encontrar a aceleração
angular da polia e a aceleração linear dos blocos.
15. Um carrossel com 2 m de raio e 500 kg.m2
de momento de inércia gira em torno de seu eixo, sem
atrito, completando uma volta a cada 5 s. Uma criança,
com 25 kg, está inicialmente no centro do carrossel e
depois caminha até a borda. Calcular a velocidade
angular que terá, então, o carrossel.
8
Física 2 – Atividade 3 -Rotação de corpos rígidos e Dinâmica do Movimento de Rotação - MHS
Torque e Momento Angular - Prof. Dr. Cláudio Sérgio Sartori
 Trabalho e potência no movimento de rotação
Podemos escrever:
dW  Ftan ds  ds  R  d
dW  Ftan R  d
P      
W     d
6000
Hz
60
f  100 Hz
  2  f    2 100    200
Podemos desenvolver:
dW    d
2
W   I    d
1
1
1
I  22  I  12
2
2
dW
d
 
dt
dt
P   
Wtot 
rad
s
1.49 105

200
1
d
dW  I    d  dW  I 
 d
dt
d
dW  I 
 d
dt
dW  I   d

f  6000rpm 
dW    d
2
P
9
  237N  m
17. Um motor elétrico desenvolve um torque
constante de  = 10 N.m sobre o esmeril montado no
seu eixo motor. O momento de inércia é I = 2.0 kg.m².
Sabendo que o sistema começa a se mover a partir do
repouso, calcule o trabalho realizado pelo motor em 8.0
s e a energia cinética no instante final. Qual a potência
média desenvolvida pelo motor?
 Solução:
  I    

I
10
rad
    2
2
s
   t
rad
  5  8    40
s
1
1
K  I   2  K  2  402  K  1600 J
2
2
1
1
    t 2    5  82    160rad
2
2
W    W  10160 W  1600J
W
1600
P
P
 P  200W
t
8
A potência instantânea P = não é constante,
porque  cresce continuamente. Porém podemos
calcular o trabalho total por:
t2
t2
W   P  dt  W       dt
t1
t1
t2
16. Um anúncio fazendo propaganda da
potência desenvolvida pelo motor de um
automóvel afirma que o motor desenvolve
1.49.105W para uma rotação de 6000 rpm. Qual
é o torque desenvolvido pelo motor?

Solução:
8
W       t  dt   10  5  tdt
t1
W  50
0
2 t 8
t
2
t 0
 W  1600 J
Física 2 – Atividade 3 -Rotação de corpos rígidos e Dinâmica do Movimento de Rotação - MHS
Torque e Momento Angular - Prof. Dr. Cláudio Sérgio Sartori
MHS – Movimento Harmônico Simples
Pêndulo Simples e Energia Mecânica
1. A corda de um piano emite um dó médio
vibrando com uma freqüência primária igual a 220 Hz.
(a) Calcule o período e a freqüência angular,
(b) Calcule a freqüência angular de um soprano
emitindo um "dó alto", duas oitavas acima, que é igual a
quatro vezes a freqüência da corda do piano.
2. Um corpo é deslocado 0,120 m da sua posição de
equilíbrio e libertado com velocidade inicial igual a
zero. Depois de 0,800 s seu deslocamento é de 0,120 m
no lado oposto e ultrapassou uma vez a posição de
equilíbrio durante este intervalo. Ache:
(a) a amplitude, (b) o período, (c) a freqüência.
3. Ao projetar uma estrutura em uma região
propensa à ocorrência de terremotos, qual deve ser a
relação entre a freqüência da estrutura e a freqüência
típica de um terremoto? Por quê? A estrutura deve
possuir um amortecimento grande 01 pequeno?
8. Um bloco de 2,00 kg sem atrito está presa a uma
mola leal cuja constante é igual a 300 N/m. Para t = O a
mola não está imprimida nem esticada e o bloco se
move no sentido negativo com 12,0 m/s. Ache:
(a) a amplitude, (b) o ângulo de fase. (Escreva uma
equação para a posição em função do tempo).
9. Repita o Exercício anterior, porém suponha que
para t = 0s o bloco possua velocidade -4,00 m/s e
deslocamento igual+0,200 m.
10. A extremidade da agulha de uma máquina de
costura se move com MHS ao longo de um eixo Ox com
uma freqüência igual a 2,5 Hz. Para t = 0 os
componentes da posição e da velocidade são +1,1 cm e 15 cm/s.
(a) Ache o componente da aceleração da agulha
para t = 0.
(b) Escreva equações para os imponentes da
posição, da velocidade e da aceleração do ponto
considerado em função do tempo.
11.
4. Um corpo de massa desconhecida é ligado a uma
mola k cuja constante é igual a 120 N/m. Verifica-se
que ele oscila com um com uma freqüência igual a 6,00
Ache:
(a) o período, (b) a freqüência angular, (c) a massa
do corpo.
x
5. Um oscilador harmônico é feito usando-se um
bloco sem atrito de 0,600 kg e uma mola ideal cuja
constante é desconhecida. Verifica-se que ele oscila
com um período igual a 0,150 s. Ache o valor da
constante da mola.
6. Temos um oscilador harmônico possui massa de
0,500 kg e uma mola ideal cuja constante é igual a 140
N/m. Ache (a) o período, (b) a freqüência, (c) a
freqüência angular.
Escreva as equações de x(t), v(t) e a(t).
7. A corda de um violão vibra com uma freqüência
igual a 40 Hz. Um ponto em seu centro se move com
MHS com amplitude igual a 3,00 mm e um ângulo de
fase igual a zero.
(a) Escreva uma equação para a posição do centro
da corda em função do tempo;
(b) Quais são os valores máximos dos módulos da
velocidade e da aceleração do centro da corda? c) A
derivada da aceleração em relação ao tempo pode ser
chamada de "arrancada". Escreva uma equação para a
arrancada do centro da corda em função do tempo e
calcule o valor máximo do módulo da arrancada.
12. Um certo pêndulo simples possui na Terra um
período igual a l,60 s. Qual é o período na superfície de
Marte onde g = 3,71 m/s2?
13. Escreva a equação diferencial do pêndulo
simples da figura e sua solução (t).
10
Física 2 – Atividade 3 -Rotação de corpos rígidos e Dinâmica do Movimento de Rotação - MHS
Torque e Momento Angular - Prof. Dr. Cláudio Sérgio Sartori
11
14.
16. Um bloco de 2,00 kg sem atrito está presa a
uma mola leal cuja constante é igual a 300 N/m. Para t
= O a mola não está imprimida nem esticada e o bloco
se move no sentido negativo com 12,0 m/s. Ache:
(a) a amplitude,
(b) o ângulo de fase
(c) Escreva uma equação para a posição em função
do tempo. (d) Escreva v(t) e a(t) em função do tempo.
2
v 
xm  x   0  ;
 0 
2
0
x  t   xm sen 0t    ;  

v0 
;
  x0 
  arctg  
k
2
;T 
m

17.
Calcule o período, a freqüência angular para um
relógio típico.
15. MHS no motor de um carro. O movimento do
pistão no interior do motor de um carro é
aproximadamente um MHS. (a) Sabendo que o percurso
(o dobro da amplitude) é igual a 0,100 m e que o motor
gira com 3500 rev/min, calcule a aceleração do pistão
no ponto final do percurso, (b) Sabendo que a massa do
pistão é igual a 0,450 kg, qual é a força resultante
exercida sobre ele neste ponto? (c) Calcule a velocidade
e a energia cinética do pistão no ponto médio do
percurso, (d) Qual é a potência média necessária para
acelerar o pistão do repouso até a velocidade calculada
no item (c)? e) Se o motor gira com 7000 rev/min, quais
são as respostas das partes (b), (c) e (d)?
(a) Encontre as expressões para a posição,
velocidade e aceleração instantânea.
Física 2 – Atividade 3 -Rotação de corpos rígidos e Dinâmica do Movimento de Rotação - MHS
Torque e Momento Angular - Prof. Dr. Cláudio Sérgio Sartori
(b) Assumindo a massa do corpo 1 kg encontre
a energia cinética e potencial elástica para x = A e x = A
/2.
(c) Qual o valor da energia mecânica?
(d) Esboce os gráficos de Ec(t), Ek(t) e Em(t)
usando o programa disponível.
Oscilações amortecidas

k
; cc  2m0
m
Amortecimento supercrítico c > cc :
Dados:
0 
x(t )  Ae1t  Be2t ; Com:
2
1. A figura mostra um tipo de oscilação amortecida
e as curvas x(t) para dois casos de subamortecimento.
Discuta quais deles possui maior constante de
amortecimento c.
1,2  
A
c
 c 
2
 
  0
2m
 2m 
v x 
x0 2  v0
; B 0 0 1
2  1
2  1
Amortecimento crítico c = cc :
x(t )  ( A  Bt)e0t ;
A  x0 ;
B  v0  0 x0
Amortecimento subcrítico c < cc
x(t )  e

c
t
2m
 A cos t  Bsent  ou

x(t )  xme
c
t
2m
sen(t   )
 c 

 cc 
2.
2
  q  0 1  
2
c
   q  0 1    ;
 cc 
 2m x0 
;
 2mv0  cx0 
  arctg 
 2mv0  cx0 
xm  x02  

 2m 
Chamamos de
amortecida:   2
período
da
2
vibração

Discuta os casos possíveis de amortecimento em função
da constante de amortecimento crítica cc e construa os
gráficos de posição x(t), velocidade v(t) e aceleração
a(t) para os seguintes osciladores livres, através do
programa do site www.claudio.sartori.nom.br:
12
Física 2 – Atividade 3 -Rotação de corpos rígidos e Dinâmica do Movimento de Rotação - MHS
Torque e Momento Angular - Prof. Dr. Cláudio Sérgio Sartori
Faça uma pesquisa sobre esse caso na
internet comentando sobre a aplicação de
vibrações forçadas.
(i) c = 0.
i
k (N/m)
m(kg)
x(t=0)
(m)
v(t=0)
(m/s)
1
2
3
4
400
1600
200
5000
1
25
5
12
0,50
0,05
0,01
0,25
1,00
0,50
0,35
0,50
Para cada caso, encontre:
(a) A freqüência f, a freqüência angular
0 ,o
400
400
400
1600
200
5000
8
40
80
65
1200
356
0,50
0,50
0,50
0,05
0,01
0,25
v(t=0)=v0
(m/s)
1
1
1
25
5
12
x(t=0)=x0
(m)
c
(N.s/m)
1
2
3
4
5
6
m(kg)
k (N/m)
período T.
(b) A velocidade máxima e a aceleração
máxima.
Construa os gráficos de posição x(t), velocidade
v(t) e aceleração a(t) para os seguintes amortecedores:
1,00
1,00
1,00
0,50
0,35
0,50
Para cada caso, encontre:
(a) A freqüência f, a freqüência angular
0 ,o
período T.
(b) A velocidade máxima e a aceleração
máxima.
3. A figura mostra a ponte de Tacoma
Narrows, destruída 4 meses e 6 dias após sua
inauguração, devido à vibrações de torção e
com
freqüência
de
ressonância
de
aproximadamente 0.2 Hz.
13