? v = ? a = E para o ângulo: ( ) 90,9 2, 42 ( ) 37,5

Problema 12.203
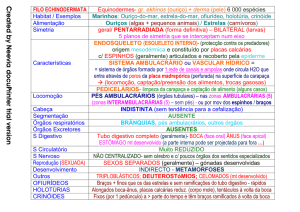
Os carros A e B se movem numa pista circular. Num dado instante,
A tem uma velocidade de 90 pés/s e essa velocidade está crescendo
a uma taxa de 15 pés/s², enquanto B, a 105 pés/s, está diminuindo sua
velocidade a uma taxa de 25 pés/s². Determine a velocidade e a
aceleração de A em relação a B nesse instante.
MECÂNICA - DINÂMICA
Cinemática de uma
Partícula
Cap. 12 - Exercícios
Prof Dr. Cláudio Curotto
Adaptado por:
Prof Dr. Ronaldo Medeiros-Junior
TC027 - Mecânica Geral III - Dinâmica
Problema 12.203 - Solução
vA = 90 pés / s
atA = 15 pés / s
2
Problema 12.203 - Solução
2
vB = 105 pés / s
atB = −25 pés / s
vA/ B = ?
a A/ B = ?
v A = −90i
Velocidade
v B = ( −105cos 60 ) i + (105sen60 ) j 
2
(at)A
y’
(an)A
v A = v B + v A/ B
(at)B
(an)B
a A = aB + a A/ B
x’
vB
y
60o
30o
60o
x
TC027 - Mecânica Geral III - Dinâmica
3
Problema 12.203 - Solução
TC027 - Mecânica Geral III - Dinâmica
4
Problema 12.203 - Solução
v A = v B + v A/ B
v A/ B = {-37,5i − 90,93 j } pés / s
v A = −90i
E para o ângulo:
v B = -105.cos 60°i + 105.sin 60° j
tgθ =
-90i = ( −52,500i + 90,933 j ) + v A/ B
v A/ B = {-37,5i − 90,93 j } pés / s
(v A / B ) y
(v A / B ) x
=
90,9
= 2, 42
37,5
37,5i
θ = 67, 6°
ϴ
90,9j
Para o módulo da velocidade:
v A/ B = 98,36 pés/s
v A/ B = ( −37, 5 )2 + ( −90,93 )2 = 98,36 pés/s
TC027 - Mecânica Geral III - Dinâmica
5
67,4o
TC027 - Mecânica Geral III - Dinâmica
6
1
Problema 12.203 - Solução
Problema 12.203 - Solução
Aceleração a A = a B + a A/ B
a A = atA + anA = −15i − 27 j
a = at + an
aB = atB + anB = ??
Tanto a aceleração do carro A quanto do B têm componentes tangencial e normal.
atA = 15 pés / s
2
atB = −25 pés / s
2
(at)A
(at)A
Carro A
(a A ) n =
y’
v² A
ρ
=
90²
= 27 pés / s ²
300
y’
(at)B
(an)A
(an)B
Carro B
x’
105²
( aB ) n =
=
= 44,1 pés / s ²
ρ
250
(an)A
vB
(at)B
(an)B
60o
x’
30o
v² B
60o
o
60o 60
y
y
x
TC027 - Mecânica Geral III - Dinâmica
7
Problema 12.203 - Solução
anB
atB
x
TC027 - Mecânica Geral III - Dinâmica
8
Problema 12.203 - Solução
atB = {( 25)( 0, 5 )} i + {( −25)( 0,866 )} j
a A = −15i − 27 j
anB = {( −44,1)( 0,866 )} i + {( −44,1)( 0, 5)} j
a B = −25, 69i − 43, 7 j
a B = {( 25 )( 0,5 ) − ( 44,1)( 0,866 )} i + {− ( 25 )( 0,866 ) − ( 44,1)( 0, 5 )} j
a A = a B + a A/ B
a B = −25, 69i − 43, 7 j
−15i − 27 j = −25, 69i − 43, 7 j + a A/ B
vB
a A/ B = 10, 69i + 16, 7 j
a A/ B =
2
(10, 69 ) + (16, 7 )
2
= 19,8 pes / s 2
60o
30o
60o
o
60o 60
atB
anB
TC027 - Mecânica Geral III - Dinâmica
9
Problema 12.203 - Solução
a A/ B = 10, 69i + 16, 7 j
a A/ B =
TC027 - Mecânica Geral III - Dinâmica
10
Problema 12.6
2
(10, 69 ) + (16, 7 )
2
Um trem de carga viaja a uma velocidade v = 60(1− e −t ) pés / s
onde t, medido em segundos, é o tempo decorrido. Determine a
distância que é coberta pelo trem em três segundos, assim como
= 19,8 pes / s 2
E para o ângulo:
16, 7
= 1,56
10, 7
θ = 57,35°
a aceleração nesse tempo.
tgθ =
16,7j
a A/ B = 19,8 pés/s
2
57,35o
ϴ
10,7i
TC027 - Mecânica Geral III - Dinâmica
11
TC027 - Mecânica Geral III - Dinâmica
12
2
Problema 12.6
Problema 12.6 - Solução
• Integração da velocidade para a obtenção da posição:
s
Dados do problema:
v(t ) = 60(1 − e − t )
v = 60(1− e −t )
v=
s = ∫ 60 − 60e − t dt
(
)
s = 60t − ( −60e ) + c
Resultados desejados:
obs : ∫ cte e − t dt = −cte e − t
( )
−t
s(3) = ?
a(3) = ?
t
ds
∴ ds = ∫ vdt
dt ∫0
0
( )
s (t ) = 60t + 60e −t + c
Solução de contorno para determinar a constante c
s (t = 0) = 0;
60 ( 0 ) + 60e −0 + c = 0 ∴ c = −60
TC027 - Mecânica Geral III - Dinâmica
TC027 - Mecânica Geral III - Dinâmica
13
Problema 12.6 - Solução
14
Problema 12.6 - Solução
• Derivação da velocidade para a obtenção da aceleração:
Posição: s (t ) = 60t + 60e −t − 60
v(t ) = 60(1 − e − t )
Para t = 3s
Posição: s (t = 3) = 60 ( 3) + 60e −3 − 60
a=
s(t = 3) = 123 pés
d ( 60 − 60e −t ) v
dt
a (t ) =
dv
dt
= 0 − ( −60e −t )
a = 60e− t
obs :
(
)
d c te ( e −t ) v
dt
(
= − cte ( e −t )
)
Para t = 3s
a ( t = 3s ) = 60e−3 = 2,99 pés / s 2
TC027 - Mecânica Geral III - Dinâmica
TC027 - Mecânica Geral III - Dinâmica
15
Problema 12.26
16
Problema 12.26 - Solução
tA para a posição de 20 pés = tB para a posição de 20 pés
Uma bola A, inicialmente em repouso, é abandonada a uma
altura de 40 pés ao mesmo tempo em que uma segunda bola
B é atirada verticalmente para cima a 5 pés
do solo. Se as bolas se cruzam a 20 pés do
solo, determine a velocidade com que a
40 pés
bola B foi arremessada. Qual a velocidade das duas bolas no
momento do encontro?
+
-g
a aceleração é constante
0
TC027 - Mecânica Geral III - Dinâmica
17
TC027 - Mecânica Geral III - Dinâmica
18
3
Problema 12.26 - Solução
Problema 12.26 - Solução
bola A:
velocidade da bolas no encontro:
bola A:
1 2
s = s0 + v0t + act
2
1
2
20 = 40 + 0 − 32, 2t
2
t = 1,1146 s
v = v0 + act ∴ vA = 0 - 32, 2 (1,1146 ) ∴ vA = -35,89 pés/s
bola B:
v = v0 + act ∴ vB = 31, 4 - 32, 2 (1,1146 ) ∴ vB = -4, 49 pés/s
bola B:
1 2
s = s0 + voB t + ac t
2
20 = 5 + vB (1,1146 ) −
1
2
( 32, 2 )(1,1146 )
2
voB = 31, 4 pés/s
TC027 - Mecânica Geral III - Dinâmica
TC027 - Mecânica Geral III - Dinâmica
19
Problema 12.45
20
Problema 12.45 - Solução
Um avião pousa numa pista a uma velocidade inicial de
110 pés / s na posição s = 0. Se a aeronave está submetida
a uma desaceleração, como indicado na figura, determine
v o =110pés/s, s=0
o tempo t' necessário para ela atingir o repouso. Construa
gráfico v-t
o gráfico v - t e s - t para o movimento. Qual a posição final do avião?
gráfico s-t
posição final?
TC027 - Mecânica Geral III - Dinâmica
t ' = ?( v = 0)
TC027 - Mecânica Geral III - Dinâmica
21
Problema 12.45 - Solução
22
Problema 12.45 - Solução
Tempo para o repouso:
tempo 0 a 5 s:
v = 110 pés/s já que a = 0
120
tempo 5 a 15 s:
100
Velocidade x Tempo
110
v = v0 + a ⋅ t
Velocidade (pés/s)
90
v = 110 pés/s + ( − 3 pés/s) (10 s )
v = 80 pés/s
tempo 15 a 20 s:
v = 80 pés/s + ( − 8 pés/s) ( 5 s )
80
70
60
50
40
30
v = 40 pés/s
tempo 20 a ? s:
0 = 40 p és/s + ( −3 pés/s) ( t )
tempo para o repouso:
20
t ' = 5 + 10 + 5 + 13, 333 s ∴ t ' = 33, 3 s
10
0
0
5
10
TC027 - Mecânica Geral III - Dinâmica
15
20
25
30
33,33
Tempo (s)
t = 13, 3 3 3 s
23
TC027 - Mecânica Geral III - Dinâmica
24
4
Problema 12.45 - Solução
Problema 12.45 - Solução
Dado o Gráfico v - t , o gráfico s - t pode ser construído
⇒ 0 a 5 s:
retângulo = 110 ⋅ 5 = 550 pés
usando-se v = ds / dt escrito na forma integral.
⇒ 5 a 15 s:
ds
v = ∴∆s = ∫ vdt = deslocamento = área do gráfico v-t
dt
trapézio =
(B + b)
(80 + 110)
⋅h =
⋅ 10 = 950 pés
2
2
⇒ 15 a 20 s:
trapézio =
∆s = deslocamento
(80 + 40)
⋅ 5 = 300 pés
2
⇒ 20 a 33,33 s:
40 ⋅ 13,33
triângulo =
= 266, 6 pés
2
∫ vdt = área sob o gráfico v - t
TC027 - Mecânica Geral III - Dinâmica
TC027 - Mecânica Geral III - Dinâmica
25
Problema 12.45 - Solução
Posição final
550 + 950 + 300 + 266, 6 = 2066, 6 pés
26
Problema 12.78
Um ponto material se move numa
Deslocamento x Tempo
2500
curva definida pela parábola
2
Deslocamento (pés)
2000
y = 0,5 x . Se o componente x
266,6
da velocidade é vx = 5t pés/s,
300
1500
onde t é dado em segundos,
950
determine a distância à origem
1000
O e o módulo da aceleração
500
quando t = 1 s.
Em t = 0, x = 0 e y = 0.
0
0
5
10
15
20
25
30
33,33
Tempo (s)
TC027 - Mecânica Geral III - Dinâmica
Problema 12.78 - Solução
y = 0,5x2
d = ? (t = 1s)
t = 0
TC027 - Mecânica Geral III - Dinâmica
27
28
Problema 12.78 - Solução
Posição x:
vx = 5t
a = ? (t= 1s)
vx =
∫
x
0
x = 0
y = 0
v=
dx
= 5t ∴ d x = 5td t
dt
t
d x = ∫ 5tdt ∴ x = 2,5t pés
2
0
Posição y:
(
2
y = 0, 5 x ∴ y = 0, 5 2,5t
d = x2 + y2
ds
∴ S = ∫ vdt
dt
2
a = ax + a y
2 2
) ∴ y = 3,125t
4
Para t = 1 s:
2
2
4
x = 2,5 (1) =2,5 pés; y = 3,125 (1) = 3,125 pés
A distância até a origem:
2
TC027 - Mecânica Geral III - Dinâmica
29
2
2
2
d = x TC027
+ y - Mecânica
= ( 2,5
3,125 ) ∴ d = 4 pés
) III+-(Dinâmica
Geral
30
5
Problema 12.78 - Solução
Problema 12.94
Aceleração:
a x = x=
a y = y=
d
2
A bola chutada em A parte formando um ângulo
( 2,5t ) = d ( 5t ) ∴ a
2
dt
d
2
dt
x
= 5 pés/s
de coordenadas x = 15 pés e y = -9 pés, determine os
(3,125t ) = d (12, 5t ) ∴ a
4
θ A = 30º com a horizontal. Se ela atinge o solo no ponto B
2
módulos da velocidade em A e em B.
3
dt
dt
y
= 37,5t 2 pés/s 2
Para t = 1 s:
2
2
ax = 5 pés/s ; a y = 37,5 (1) ∴ a y = 37,5 pés/s
2
O módulo da aceleração:
a = ax 2 + a y 2 =
2
( 5) + ( 37,5)
2
∴ a = 37,8 pés/s 2
TC027 - Mecânica Geral III - Dinâmica
31
Problema 12.94 - Solução
Ponto B
TC027 - Mecânica Geral III - Dinâmica
32
Problema 12.94 - Solução
x = 15 pés
y = -9 pés
Movimento parabólico Velocidade na direção x constante e
ax = 0
vx = v Ax = vBx
θ A = 30 o
vA = ?
Em y a aceleração é constante = -g = -32,2 pés/s2.
vB = ?
TC027 - Mecânica Geral III - Dinâmica
33
Problema 12.94 - Solução
TC027 - Mecânica Geral III - Dinâmica
Problema 12.94 - Solução
No movimento horizontal:
Decompondo o vetor velocidade em A:
v Ax = vx = v A .cos 30º
(1)
1
s = s0 + v0t + ac t 2
2
v Ay = v A .sen 30º
(2)
xB = x A + vxt AB → 15 = 0 + vx t AB ∴ vx =
vAy
Logo:
v Ay
v Ax
=
v A .sen 30º
= tg30º
v A .cos 30º
v Ay = v Ax tg30º
34
15
t AB
(4)
No movimento vertical:
1
yB = y A + v Ay t AB + ( − g )t AB 2
2
32, 2 2
−9 = 0 + v Ay t AB −
t AB
(5)
2
vAx
(3)
TC027 - Mecânica Geral III - Dinâmica
35
TC027 - Mecânica Geral III - Dinâmica
36
6
Problema 12.94 - Solução
Problema 12.94 - Solução
Substituindo (3) em (5):
vx =
−9 = vx tg 30o t AB − 16,1t AB 2
15
= 14,32 pés / s
1, 047
Substituindo (4):
Substituindo em (1):
15
−9 =
tg 30o t AB − 16,1t AB 2
t AB
vx = v A .cos 30º∴ v A =
t AB 2 =
14, 32
= 16, 5 pés / s
cos 30º
Para determinar vB
9 + 15tg 30o
∴ t AB = 1, 047 s
16,1
vB = vBx 2 + vBy 2
Substituindo tAB em (4):
vx =
Velocidade em x é cte; a = 0
Logo:
15
= 14,32 pés / s
1, 047
vBx = 14,32 pés / s
TC027 - Mecânica Geral III - Dinâmica
37
Problema 12.94 - Solução
2
2
v A = 16,5 pés / s
Substituindo (2):
vB = 29, 2 pés / s
2
vBy 2 = ( v A sen30o ) + 579, 6
o 2
(16,5sen30 )
38
FINAL (Resposta):
vBy 2 = v Ay 2 − 2 ( 32, 2 )( −9 − 0 )
vBy =
TC027 - Mecânica Geral III - Dinâmica
Problema 12.94 - Solução
v = v0 + 2ac ( s − s0 )
Para determinar vBy:
vBx = v Ax = vx
+ 579, 6 = 25, 45 pés / s
Para determinar vB
vB = vBx 2 + vBy 2 =
2
(14,32 ) + ( 25, 45)
2
= 29, 2 pés / s
TC027 - Mecânica Geral III - Dinâmica
39
TC027 - Mecânica Geral III - Dinâmica
40
Problema 12.106
O avião a jato desloca-se na trajetória
parabólica mostrada na figura. Quando
ele passa pelo ponto A, sua velocidade
Exercícios que serão resolvidos na
próxima aula
é de 200 m/s e está crescendo a uma
taxa de 0,8 m/s 2 . Determine o módulo
da aceleração do jato no ponto A.
TC027 - Mecânica Geral III - Dinâmica
41
TC027 - Mecânica Geral III - Dinâmica
42
7
Problema 12.106
Problema 12.206
Um passageiro num automóvel a 60 km/h observa que as gotas de chuva
RESPOSTA
o
formam um ângulo de 30 com a horizontal. Calcule a velocidade da
chuva supondo que ela é constante e cai verticalmente.
a = 0, 92 m/s
2
TC027 - Mecânica Geral III - Dinâmica
43
Uma pessoa deve ser transportada em um elevador até o quarto
andar de um estacionamento que está a 48 pés acima do solo.
Se o elevador pode acelerar a 0,6 pés/s², desacelerar a
0,3 pés/s² e atingir uma velocidade máxima de 8 pés/s,
determine o menor tempo em que o elevador faz o transporte,
partindo do repouso e terminando em repouso.
RESPOSTA
vchuva = 34, 6 km/h
45
Problema 12.9
TC027 - Mecânica Geral III - Dinâmica
46
Problema 12.9 - MODIFICADO
Uma pessoa deve ser transportada em um elevador até o décimo
andar de um estacionamento que está a 180 pés acima do solo.
Se o elevador pode acelerar a 0,6 pés/s², desacelerar a
0,3 pés/s² e atingir uma velocidade máxima de 8 pés/s,
determine o menor tempo em que o elevador faz o transporte,
partindo do repouso e terminando em repouso.
RESPOSTA
t=21,9 s
TC027 - Mecânica Geral III - Dinâmica
44
Problema 12.9
Problema 12.206
TC027 - Mecânica Geral III - Dinâmica
TC027 - Mecânica Geral III - Dinâmica
47
TC027 - Mecânica Geral III - Dinâmica
48
8
Problema 12.9 - MODIFICADO
Problema 12.48
O gráfico mostra a velocidade de um carro em função do tempo.
RESPOSTA
Determine a distância total percorrida até o repouso. Construa o
gráfico a - t.
t=42,5 s
TC027 - Mecânica Geral III - Dinâmica
49
Problema 12.48
TC027 - Mecânica Geral III - Dinâmica
50
Problema 12.190
A menina situada em C puxa a corda horizontalmente a uma velocidade
RESPOSTA
constante de 6 pés/s. Determine a velocidade escalar do bote no instante
em que o trecho AB da corda tem 50 pés.
a (m/s 2 )
−0, 250
TC027 - Mecânica Geral III - Dinâmica
t (s)
51
TC027 - Mecânica Geral III - Dinâmica
52
Problema 12.190
RESPOSTA
vB = x B = −6, 08 pés/s
TC027 - Mecânica Geral III - Dinâmica
53
9