Questão 23.

Questão 23.
Uma mangueira, com bico a 1.5m acima do solo, é apontada para cima, segundo
um ângulo de 30o com o chão. O jato de água atinge um canteiro a 15m de
distância.
a) Com que velocidade o jato sai da mangueira?
b) Que altura ele atinge?
Resolução:
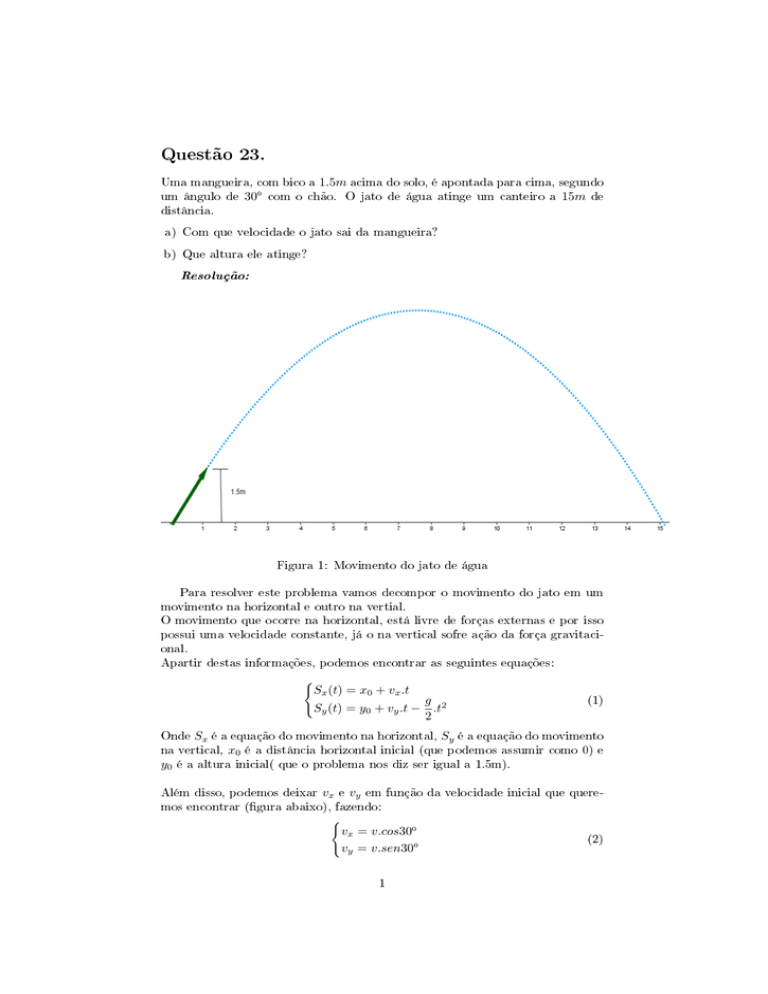
Figura 1: Movimento do jato de água
Para resolver este problema vamos decompor o movimento do jato em um
movimento na horizontal e outro na vertial.
O movimento que ocorre na horizontal, está livre de forças externas e por isso
possui uma velocidade constante, já o na vertical sofre ação da força gravitacional.
Apartir destas informações, podemos encontrar as seguintes equações:
(
Sx (t) = x0 + vx .t
g
Sy (t) = y0 + vy .t − .t2
2
(1)
Onde Sx é a equação do movimento na horizontal, Sy é a equação do movimento
na vertical, x0 é a distância horizontal inicial (que podemos assumir como 0) e
y0 é a altura inicial( que o problema nos diz ser igual a 1.5m).
Além disso, podemos deixar vx e vy em função da velocidade inicial que queremos encontrar (gura abaixo), fazendo:
(
vx = v.cos30o
vy = v.sen30o
1
(2)
Figura 2: Decomposição de v
Substituindo vx = v.cos30o e considerando o espaço nal percorrido horizontalmente pela água como xf = 15 m em (1), encontramos o tempo tf que o
jato de água demora para sair da mangueira e voltar ao chao.
xf = v.cos30o .tf ⇒ tf =
xf
v.cos30o
(3)
Substituindo agora tf na equação do movimento vertical e fazendo vy =
v.sen30o e Sy (tf ) = 0 (jato de água encosta no chão), conseguimos uma expressão para v :
g
v
xf
g
xf
0 = y0 + v.sen30o .tf − .t2f ⇒ 0 = y0 + .
− (
)2 ⇒
2
2 v.cos30o
2 v.cos30o
2.g.x2f
4.g.x20
xf
2.v.x0
√ −
√
⇒
0
=
y
+
−
⇒
0 = y0 +
0
2
3.v 2
2.v.
3
√ 3 2 6.v
2. 3.g.xf
√
v2 =
3.(y0 . 3 + xf )
Substituindo os valores de xf e y0 e considerando g ≈ 10m/s2 temos que
v ≈ 12m/s. (a).
Para encontrarmos a altura máxima, utilizamos a Equação de Torricelli:
vf2 = vi2 + 2.a∆S
Como a velocidade quando a altura é máxima é igual a zero e a velocidade
inicial na vertical é v/sen30o = v/2 = 6m/s, substituindo temos que:
v
0 = ( )2 − 2.g.∆S ⇒ ∆S = 1.8m
2
Como a altura inicial é 1.5m, temos que a altura máxima total é 1.5m +
1.8m = 3.3m (b).
Integrantes:
Thiago Rodrigo Ramos
Guilherme Trajano de Santana
Elizabete Dutra Valle
2