Aula 02 - Centro de Estudos Espaço

Notas de Aula 2 – Dinâmica dos Sólidos – Prof. Dr. Cláudio S. Sartori
M
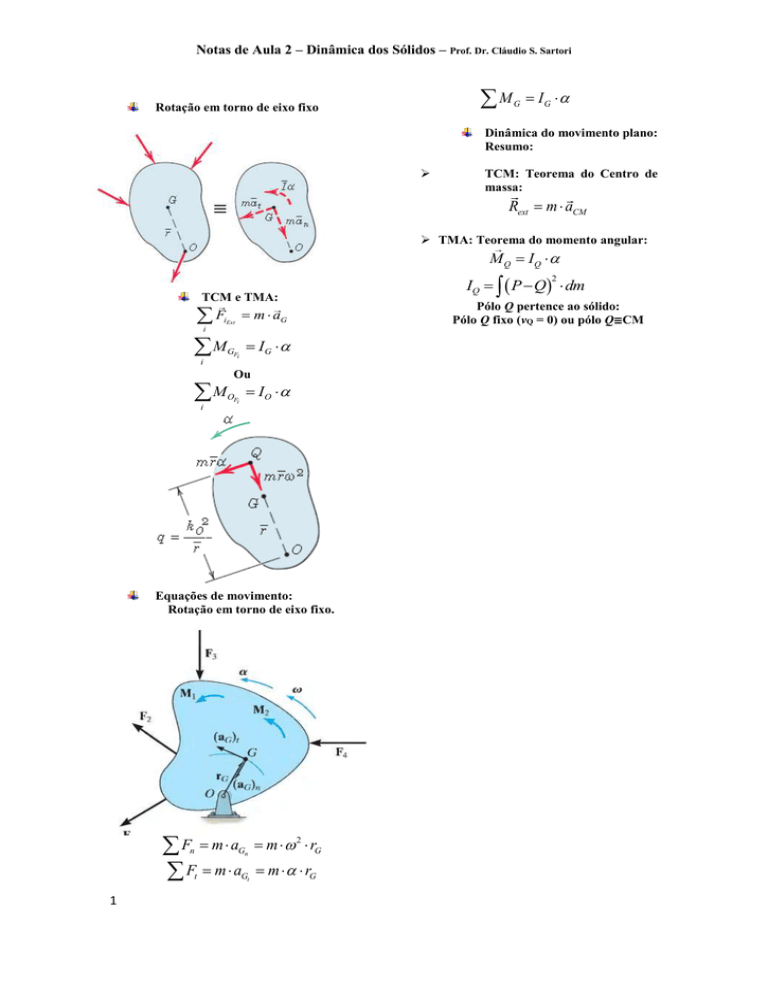
Rotação em torno de eixo fixo
G
 IG 
Dinâmica do movimento plano:
Resumo:

TCM: Teorema do Centro de
massa:
Rext  m  aCM
 TMA: Teorema do momento angular:
M Q  IQ  
IQ    P  Q  dm
2
TCM e TMA:
F
 m  aG
iExt
i
M
i
 IG  
GFi
Ou
 MOF  IO 
i
i
Equações de movimento:
Rotação em torno de eixo fixo.
 F  ma
 F  ma
1
n
Gn
 m   2  rG
t
Gt
 m    rG
Pólo Q pertence ao sólido:
Pólo Q fixo (vQ = 0) ou pólo QCM
Notas de Aula 2 – Dinâmica dos Sólidos – Prof. Dr. Cláudio S. Sartori
m
aA  ac  26  ˆj  2  
s 
1. (Beer Johnston 10a Ed. Pag. 1052) - Um fio é
enrolado em torno de um disco de raio r homogêneo
0.5 m e de massa de 15 kg. Se o cabo é puxado para
cima, com uma força de intensidade T = 180 N,
determinar (a) a aceleração do centro do disco, (b)
a aceleração angular do disco, (c), a aceleração do
cabo.
 F  ma
i
G
2. (Beer Johnston 10a Ed. Pag. 1053) - Uma esfera
uniforme de massa m e raio r é projetada ao longo
de uma superfície horizontal áspera com uma
velocidade linear v0 e sem velocidade angular.
Denotando por k o coeficiente de atrito cinético
entre a esfera e o chão, determine (a) o tempo t1 em
que a esfera vai começar a rolar sem deslizar, (b) a
velocidade linear e a velocidade angular da esfera
no tempo t1.
 m  ay  T  P
i
m g
ay 
TP
180  150
m
 ay 
 ay  2 2
m
15
s
⤹  M
G
 IG 
T  R  IG  
F
iExt
i

m  aGx    N  a    g
 m  aG  

 N  P  0  N  m g
 M O  IG  
i
2
IG  m  r 2
5
 M O  IG  
M  R2
15  0.52
IG 
 IG 
 I G  1.875kg  m2
2
2

T  R
180  0.5
rad
  
   48 2 ↻
IG
1.875
s
aGx  0  aGy  2
m

s2
Inicialmente v =  = 0
aP  aQ     P  Q       P  Q
aA  aG     A  G        A  G 


a A  2  ˆj  48  kˆ  0.5  iˆ  0
aA  2  ˆj  24  kˆ  iˆ  aA  26  ˆj
ˆj
2
i
2
F  r  m  r 2 
5
2
  m  g  r  m  r 2  
5
2
5 g
  g  r      
5
2 r
A esfera começará a rolar sem deslizar
quando o ponto de contato dela com o solo possuir
velocidade nula.
vC  0
t  0  v  v0
v  t   v0  a  t
Notas de Aula 2 – Dinâmica dos Sólidos – Prof. Dr. Cláudio S. Sartori
vG  t   v0    g  t
a aceleração vertical do bloco e a força resultante
sobre o rolamento em O.
vC  vG    GC
0  vG  iˆ    kˆ  r  ˆj
0  vG  iˆ    r  kˆ  ˆj
 iˆ
0  iˆ  vG  iˆ    r  iˆ  vG    r
v0    g  t    r
  t   0    t
5 g
  t   0 
t
0
2 r
5 g
t
2 r
5 g
v0    g  t   
t  r
2 r
5
v0    g  t    g  t
2
2v0
7
  g  t  v0  t  t1 
2
7  g
 t   

I0  k 2  m  I0  k 2 
Velocidade linear
vG  t   v0    g  t
vG  t  t1   v0    g 
2v0
7  g
I0  k 2 
k  18in  k 
7v  2v0
2
vG  t  t1   v0  v0  vG t  t1   0
7
7

5 g
t
2 r
5   g 2v0
  t  t1   

2 r 7  g
5v
  t  t1    0
7 r
Tomando o centro de rotação O:
M
O
 IO  
i
 12 
 24 
T     400     22.5  
 12 
 12 
800 T  22.5
A aceleração do bloco será:
F
iext
3
18
ft
ft  g  32.3 2
12
s
2
 t   
3. (Meriam Kraige pag. 432) - O bloco de concreto de
peso 644 lb é elevado pelo mecanismo mostrado de
içar, onde os cabos estão firmemente enrolados em
torno dos respectivos tambores. Os cilindros, que
são mantidos juntos a girar como uma unidade única
sobre o seu centro de massa, em O, têm um peso
combinado de 322 lb e um raio de giração de cerca
de 18 in. Se uma tensão constante de P = 400 lb é
mantida pela unidade de potência em A, determinar
P
g
 18  322
I0    
 12  32.2
I0  22.5lb  f  s2
5
vG  t  t1   v0
7
Velocidade angular:
P
g
 m  aG  T  P  m  a
i
644 lb
T  644 
P
644
 a  T  644 
a
g
32.2
32.2
ft
s2
 12 
a    r  a    
 12 
Resolvendo:
Notas de Aula 2 – Dinâmica dos Sólidos – Prof. Dr. Cláudio S. Sartori
IG  0.559lb  ft  s2  IG  0.559slug  ft 2
800  T  22.5
T  644 
644
a
32.2
20
800  T

22.5
 800  T 
T  644  20  

 22.5 
22.5T  22.5 644  20 T  20  800
22.5T  20 T  22.5 644  20  800
42.5T  14490 16000
30490
T
 T  717lb
42.5
800  T
800  717

 
22.5
22.5
rad
ft
  3.67 2  a  3.67 2
s
s
Equilíbrio no centro da polia:
F
ix
F
iy
 Ox  400  cos 450  0
Teorema de Steiner ou dos eixos paralelos:
IO  IG  m d 2
50
I O  0.559 
 0.52
32.2
1.5527
IO  0.94719slug  ft 2
M
i
 Oy  822  717  400  sen45  0
0

i
i
Como  = 0: (roda parte do repouso):
Ox  283lb  Oy  1322lb
O  O  O  O  1352lb
2
y
On  0


  Fti  m  at    Fti  m    rG
i
4. (Hibbeler 12a Ed. Cap. 17 pag. 428 ) - Uma
roda desbalanceada de 50 lb possui um raio de
giração kG = 0.6 ft sobre um eixo passando através
de seu centro de massa G. Se a roda parte do
repouso, determine as reações sobre seu pino O.
rad
s2
  Fni  m  an    Fni  m   2  rG
i
2
x
 IO  
50  0.5  0.94719      26.3938

i
OFi
i
Ot  50  m   rG
Ot  50  1.5527   26.39   0.5
Ot  50  20.487  Ot  29.51lb
5. (Hibbeler 12a Ed. Cap. 17 pag. 429 ) - Uma
barra de 20 kg num certo instante possui velocidade
angular  = 5 rad/s. Determinar as reações na
conexão da barra em O e a aceleração angular. Use
g = 9.81 m/s².
Diagrama de corpo livre:
Momento de Inércia:
I G  m  kG2  I G 
IG 
4
P 2
 kG
g
50  lb 
2
 0.62  ft 
 ft 
32.2  2 
s 
Notas de Aula 2 – Dinâmica dos Sólidos – Prof. Dr. Cláudio S. Sartori


  Fni  m  an    Fni  m   2  rG
i
i
On  m   rG
2
On  20  52 1.5  On  750N


  Fti  m  at    Fti  m    rG
i
i
Ot  P  m   rG
Ot  P  m    rG
209.81
20
↺  M F
iG
i
1.5
 IG  
ml2

12
20  32
60  196.2  30    1.5 

12
60  Ot 1.5 
180
60  294.3  45   
  60    354.3
12


  Fxi  m  an    Fxi  m   2  rG
i
15



Equações de movimento para o tambor:

i
Ox  m   rG
2
354.3
rad
   5.905 2
60
s

Ot  196.2  20  5.905 1.5  Ot  372.35N

  Fyi  m  a y    Fyi  m    rG
i
177.15
i
Oy  P  T  m   rG
Usando:
M
i
FiO
Oy  T  P  m    rG
 IO  
609.81
↺  M F
m l2
m l2
l
IO 
 m     IO 
12
3
2
2
20  32
IO 
 I O  60kg  m 2
3
rad
s2
6. (Hibbeler 12a Ed. Cap. 17 pag. 430 ) - O
tambor mostrado possui massa de 60 kg e raio de
giração k0= 0.25 m. Uma corda de massa
desprezível é presa ao tambor e a uma massa de 20
kg. Se o bloco é abandonado, determine a
aceleração angular do tambor.
i
iO
 IO  
Momento de inércia do tambor:
IO  m kO2  IO  60  0.252  IO  3.75kg  m2
T  r  IO  
0.4
T  0.4  3.75     
T
3.75
Se a corda não se desliza sobre a polia, a
aceleração tangencial da polia será a mesma do
bloco: a    rG

Equação de movimento para o bloco:

  Fyi  m  a y  Pb  T  m  a
i
5
0.4
Oy  T  588.6  24 
IO  IG  m d 2
60  20  9.811.5  60      5.905
60
Notas de Aula 2 – Dinâmica dos Sólidos – Prof. Dr. Cláudio S. Sartori
20  9.81 T  20  a 196.2  T  20  a
196.2  T
a
20
a
   
rG
196.2  T
196.2  T
20
 
0.4
8
(a) o momento das forças dissipativas, no
regime de trabalho;
(b) o momento de inércia do ventilador;
(c) o tempo gasto até o ventilador parar,
após ser desligado.
0.4
196.2  T 0.4
T

T
3.75
8
3.75
196.2  T   3.75  8  0.4  T

F
d
196.2  3.75  3.75T  3.2  T
735.75   3.2  3.75  T
T

735.75
 T  105.86 N
6.95
0.4
0.4
T  
105.86
3.75
3.75
  11.29
rad
m
 a    rG  a  4.51 2
2
s
s
0.4
6. (Livro Unip pg. 78 3.10) - 3 hastes finas,
homogêneas, cada qual com massa m e
comprimento L foram utilizadas na construção de
um triângulo, conforme ilustrado. Pede-se o
momento de inércia em relação a um eixo ortogonal
ao plano da figura e que passe pelo CM – Centro de
massa.
Potência transferida pela força resultante F:
Pmotor  F  v
Momento do motor:
Mmotor  F  d
Como v    d
Pmotor  F    d
Pmotor  Mmotor  
Na frequência de regime:
  2  f    2 
L
Pmotor  M motor    M motor 
L
CM
M motor
L
I  3 I _  I _  I /  I \ 
I_ 
1 l 3 
ml
 m  

12
3 2 
2
I CM
2
m l2

2
7. (Livro Unip pg. 83 3.11) - Um ventilador,
ao ser ligado, parte do repouso com aceleração
constante, e atinge frequência f = 3000 rpm em 5 s,
com o motor gerando potência média Pm = 350 W.
Para manter a frequência de regime de trabalho, o
motor desenvolve potência constante Pmotor = 120
W. Considerar que o valor médio, do momento das
forças dissipativas, nos movimentos acelerados,
seja 75% daquele no movimento de regime de
trabalho; pedem-se:
6
3000
rad
   314.16 
60
s
Pmotor

120

 M motor  0.3819N  m
314.16
TMA:
M R  Mmotor  Mdiss  ICM 
No regime de trabalho, a velocidade
angular é constante:  = 0. Logo:
Mmotor  Mdiss  0  Mdiss  Mmotor  0.382N  m
Considerando o movimento inicial, desde
o repouso até a frequência de trabalho:
  0    t  314.16  0    5
314.16
rad
 lig  62.832 2
5
s
2
 t
  0  t 
2
2
62.832  5
  0  5 
   785.4rad
2
Emotor   Pmootor dt

Notas de Aula 2 – Dinâmica dos Sólidos – Prof. Dr. Cláudio S. Sartori
Emotor  350  t  Emotor  1750 J
(a)
5
Energia dissipada:
Ediss   Pdiss dt  Ediss   M diss  dt
Ediss    0.382  0.75  dt
IO  1104 kg  m2
Ediss  0.287   dt  Ediss  0.287  785.38
(b)
Somas

Ediss  225.4J
Potência resultante:

PR  M R  
Energia transferida ao sistema
armazenada na forma de energia cinética:
e
Ec   PR dt  EC   M R  dt
Ec   I    dt
Ec   I 
d
 dt  Ec   Id
dt
L2
L2
 m2
2
2
2
IO  0.01 0.05  0.03 0.052
I O  m1
Massa
(kg)
m1 = 0.01
m2 = 0.03
 mi  0.04
x
(m)
0
0.1
mi.xi (kg.m)
0
0.003
 mi  xi  0.003
m1  x1  m2  x2
m1  m2
0.01 0  0.03  0.1
xCM 
0.01  0.03
0.003
xCM 
 xCM  0.075m
0.04
xCM 
I  2
I  314.162
 Ec 
 Ec  49348.2  I
2
2
Pela conservação da energia:
Ec 
EC  Em  Ediss  49348.2  I  1750  225.4
I
1524.6
 I  0.031kg  m2
49348.25
CM
Pelo TMA, com o motor desligado:
M R  I   0.287  0  0.031
0.287
rad

   9.26 2
0.031
s
  0    t  0  314.16  9.26  t
314.16
t
 t  33.93s
9.26
8. (Livro Unip pg. 67 3.01) - Duas esferas de
massas m1 = 0.010 kg e m2 = 0,03 kg estão
localizadas nas extremidades de uma haste de peso
desprezível, com comprimento L = 0,10 m.
Determinar o momento de inércia (em kg.m2):
(a) em relação a um eixo vertical passando
pelo ponto médio da haste.
(b) em relação a um eixo paralelo do item
anterior que passa pelo centro de massa do
conjunto.
0.075
0.025
ICM  0.01 0.0752  0.03 0.0252
ICM  7.5105 kg  m2
9. (Livro Unip pg. 83 3.04) - Um balão
esférico de raio R é constituído por uma película
fina e homogênea de massa m. Considerando um
eixo radial, pedem-se:
(a) o momento de inércia;
(b) o raio de giração.
(a)
2
ICM  m  R2
3
(Esfera oca)
(b) ICM  2 m  R2  m  k 2  k  2 R
3
3
y
10. (Livro Unip pg. 83 3.11) - Uma barra
homogênea ilustrada a seguir, de massa m e
comprimento L, está articulada pela extremidade A,
girando em um plano vertical, sob ação de um
x
7
Notas de Aula 2 – Dinâmica dos Sólidos – Prof. Dr. Cláudio S. Sartori
momento M. No instante ilustrado a velocidade
angular é  = 8 rad/s; para esse instante, determine:
(a) a aceleração angular da barra (em
rad/s2).
(b) as componentes da reação na
articulação.
Dados: m = 40 kg; L=6 m
M = +120 N.m g = 10 m/s2
11. (Livro Unip pg. 107 3.29) - Os blocos
ilustrados a seguir têm massas m1 e m2. A massa da
polia é mp e seu raio é R. Desprezar a massa da corda
e admitir que não há escorregamento entre a corda
e a polia. Considere a aceleração da gravidade local
igual a 10 m/s2. A aceleração do bloco de massa
m1 vale aproximadamente, em m/s2:
Dados: m1 = 20 kg m2 = 12 kg M = 8 kg
R = 0.3 m
y
y
ax
H
x
x
ay
V

P
TCM.: Teorema do centro de massa:
F
xi
i
F
yi
 m   ax   H  m  ax
 m   a y   V  P  m  a y
i
 TMA: Teorema do momento angular:
M
FiO
yi
i
 P  T  m1  a
 m1  a1   1 1
T2  P2  m`2  a
 TMA: Teorema do momento angular:
M
I O  I CM  m  OG  I O 
m l2
l
 m 
12
2
2
40  62
IO 
 I O  480kg  m2
3
6
120  400   480  
2
rad
↻
s2
m
s2
L2
m
a y    r  a y  2.25  3  a y  6.75 2
s
L2
ax   2  r  ax  82  3  ax  192
H  40   192   H  7680 N
V  400   40  6.75  V  400  270
270
V  130N
 IO  
T1  T2   R 
mp  R 2
2

O=G ; P1 = m1.g = 200N
P2 = m2.g = 120N
Como a corda não escorrega:
a1  a2    R
ml2 ml2
m l2

 IO 
12
4
3
1080  480      2.25
FiO
T1  R  T2  R  IO 
O=A ; P = m.g = 400N
 Teorema dos eixos paralelos:
8
F
i
6
120  400   IO  
2
IO 
TCM.: Teorema do centro de massa:
 IO  
i
2

T1  T2   R 
mp  R 2

2
200  T1  20  a

T2  120  12  a
mp  R2 a

T1  T2   R 
2
R
0.36
T1  T2 
mp
2
 a  a  T1  T2  

T1  T2 
200  T1  20 
4

T  120  12  T1  T2 
 2
4
200  T1  5  T1  5  T2

T2  120  3  T1  3  T2
2
8
Notas de Aula 2 – Dinâmica dos Sólidos – Prof. Dr. Cláudio S. Sartori
6  T1  5  T2  200

 4  T2  3  T1  120
8  1.5 
8  T2  5  T2  200  240
200  5  T2
440
T2 
N  T1 
3
6
6  0.42
6.5 rad
   
2
0.48 s 2
13.54
0.48
    2  
2
F
2
0
402  0  2 13.54     
146.67
T1 
59.08
440
3  T  2800 N
1
6
18

59.08
n
n
 n  9.4
2
2
200  5 
155.56
T1  T2
155.56 146.67
a
4
4
T1  T2
155.56 146.67
a
a
4
4
m
a  2.22 2
s
a
12. (Livro Unip pg. 91 3.14) - Um disco
uniforme, com eixo fixo, possui raio R = 0,4 m e
massa m = 6 kg. Em repouso, o disco é acionado pea
força F = 20 N, através de uma corda enrolada no
mesmo. O atrito nos mancais, gera um binário
(momento) resistente Mres = 1.5 N.m. Pedem-se:
(a) a reação do eixo fixo.
(b) o número de voltas necessária para que
o disco atinja a velocidade angular de  = 40 rad/s.
1600
rad
27.08
13. (Beer Johnston 5 Ed. 16.5 Pag. 551) –
Uma polia pesando 53.4 N e raio de giração 0.203
m está unida a dois blocos como ilustrado.
Supondo-se que não exista atrito no eixo,
determinar a aceleração angular da polia e a
aceleração de cada cilindro.
0.254 m
0.152 m
44.5 N
22.2 N

Sentido do movimento: Para manter a
polia em equilíbrio:
⤹  M
G
 0  PB  0.152  22.2  0.254  0
PB  37.1N
A polia girará no sentido antihorário.

TCM.: Teorema do centro de massa:
H  m  ax


0

V  P  F  m  a y
0

H 0


V  60  20  0  V  80 N
 TMA: Teorema do momento angular:
M
FiO
 IO  
i
F  R  MRes  ICM 
m  R2
20  0.4  1.5 

2
9

Cinemática do movimento:
aA    rA  aB    rB
aA  0.254   aB  0.152  
FRB  mB  aB  PB  TB
TB  PB  mB  aB  TB  44.5  4.536  0.152  
PB g
TB  44.5  0.6895 
FRA  mA  aA  TA  PA
Notas de Aula 2 – Dinâmica dos Sólidos – Prof. Dr. Cláudio S. Sartori
TA  mA  aA  PA  TA  2.2629  0.254    22.2
PA g
TA  0.5748   22.2
 Equações de movimento: momento de
inércia da polia:
I  mk2  I 
I
P 2
k
g
53.4
 0.2032  I  0.224kg  m2
9.81
⤹  M
G
  Fyi  m  a
 IG 
i
100  T  78.48  8  aG
TB  0.152  TA  0.254  IG 
P m g
 44.5  0.6895    0.152
  0.5748   22.2  0.254  0.224 
6.764  0.1048  
0.146    5.6368  0.224  
1.1272  0.2508  0.224
1.1272 rad
 0.2508  0.224   1.1272   
0.4748 s 2
2.37
  2.37
rad
↺
s2
m

s2
m
aB  0.152  2.37  aB  0.360 2 
s
a A  0.254  2.37  a A  0.602
14. (Hibbeler pag.442 17.13) – Determine a
aceleraçãoangular da polia da figuram que possui
uma massa de 8 kg e raio de giração kG = 0.35 m. A
massa da corda é negligenciável.
8 9.81
Para que a polia não escorregue em A:
aG    r  aG    0.5
21.52  T  8 0.5
21.52  T

4
 21.52  T 
T  0.5  20  0.98  

4


4 T  0.5  20   0.98   21.52  T 
2 T  80  21.0896  0.98T
58.91
T
 T  19.76N
2.98
21.52  19.76
rad

   10.32 2
4
s
m
aG  5.16 2
s
15. (Livro Unip pg. 109 3.32) - A figura ilustra
uma barra AB, homogênea , de massa m = 20 kg e
comprimento L = 0.5 m. Na posição definida pelo
ângulo  = 600, a mesma apresenta velocidade
angular  = 4 rad/s. Pede-se a aceleração angular da
barra.
A
s

CM
L/2
L/2
 Equações de movimento: momento de
inércia da polia:
I  m  k 2  I  8  0.352
N
0.98kg m2
⤹  M
G
10
n̂
tˆ
A=O
 IG 
T  0.5 100  0.2  0.98
B
T
L/2
P.cos


CM
L/2
B
Notas de Aula 2 – Dinâmica dos Sólidos – Prof. Dr. Cláudio S. Sartori


Diagrama de corpo livre:
P


P.sen

TCM: Teorema do centro de massa:
 Fni  N  P  sen  m  an
 i

  Fti  P  cos   T  m  at
 i
L
an   2  rG  rG 
2
L
at    rG  rG 
2
TMA: Teorema do Momento Angular
 M Fi  IO 
i
O
L
IO  IG  m   
2
IO 
2
m  L2 m  L2
m  L2

 IO 
12
4
3
L m  L2
 P  cos   

2
3
L m  L2
3  g  cos 

    
2
3
2 L
0
3 10  cos 60
rad
 
   15 2
2  0.5
s
m  g  cos  
F
F
P
Fat
N


 0.5 
    75.96
 0.125 
  90   90 75.96   14.04
  arctg 

TCM: Teorema do centro de massa:
(disco)
  Fxi   F  cos14.04  Fat  m  aGx
 i

 Fyi  F  cos 75.96  N  P  m  aGy
 i
F  cos14.04  Fat  0

 0.245  F  N  40  0
Calcule os valores de N e T agora, carinha....
aT   
L
3  g  cos
 aT 
2
4
L
an   
2
2
16. (Livro Unip pg. 109 3.33) - O disco de raio
r = 0.125 m e massa m = 4 kg, momento de inércia
baricêntrico ICM = 0.052 kg.m², inicialmente em
repouso, é colocado em contato com a esteira, que
move-se com velocidade constante, para a direita, v
= 3 m/s. O coeficiente de atrito entre a esteira e o
disco é  = 0.40, pedem-se:
(a) determinar a aceleração angular do
disco durante o escorregamento;
(b) o ângulo total de rotação do disco,
desde o repouso, até que o escorregamento do disco
e a esteira cesse.

TMA: Teorema do Momento Angular
 M Fi  IO 
i
O
Fat  0.125  IG 
  N  0.125  I G    0.05  N  0.052  
0.4
0.052
N  1.04 
 F  cos14.04  1.04      0

0.97
0.4


 0.245  F  1.04    40  0
0.97  F  0.416    0

 0.245  F  1.04    40
0.97


F

0.416

2.32

0.245

F

1.04
 2.32  F  40

rad

  2.332  F    35 2

s


40 N
0.245  F  2.425  F  40  F 
2.6578

15.05

N  1.04  35  N  36.3N
11
Notas de Aula 2 – Dinâmica dos Sólidos – Prof. Dr. Cláudio S. Sartori
O escorregamento cessa quando
velocidades das superfícies forem iguais:
as
vBordaDisco  vesteira  final  r  3
3 rad
 final  0.125  3   final 
0.125 s
24

2
final

2
inicial
 2    
242  2  35     
576
rad
70
8.23
17. (Livro Unip pg. 102 3.20) - O sistema de
polias duplas tem momento de inércia total ICM =
20.3 kg.m², raio interno Ri = 0.23 m e raio externo
Re = 0.40 m, respectivamente; inicialmente em
repouso,é acionado por um contrapeso de massa m
= 65 kg. Pedem-se:
(a) a aceleração angular do sistema;
(b) a velocidade angular no instante t = 3 s;
(c) a velocidade angular no instante em que o
contrapeso deslocou-se de 0.3 m.

Diagrama de corpo livre:
T  R  20.3    T 
aT  R 
20.3  
R
P  T  m  aG
20.3
R
6510
65
R
20.3  
 65  0.23  
0.23
650  88.26   14.95
650
rad

   6.3 2
88.26  14.95
s
  0    t
rad
  0  6.3  3    18.9
s
2
2
  0  2  
s
s    R   
R
0.3
 
   1.3rad
0.23
2  0  2  6.31.3    16.43
rad
  4.05
s
650 
18. (Livro Unip pg. 94 3.16) - A polia dupla
ilustrada tem raios R1 = 0.6 m e R2 = 1.2 m, massa
mP = 600 kg, raio de giração k = 0.9 m, e é acionada
através de uma corda que faz um ângulo  = 60°
com a horizontal, com tração F = 3600 N. O
movimento da polia, suspende o bloco de massa mB
= 300 kg. Considerar que as cordas não
escorreguem em relação à polia e g = 10 m/s².
Pedem-se:
(a) a aceleração do bloco;
(b) as componentes horizontal e vertical da
reação do eixo.
T
Pp
P


TCM: Teorema do centro de massa:
Contra Peso
F
yi
 P  T  m  aG
R2
R1
mB
i

TMA: Teorema do Momento Angular
 M Fi  IO 
i
12
O
V
H
F
Notas de Aula 2 – Dinâmica dos Sólidos – Prof. Dr. Cláudio S. Sartori
H
TB
PP
TB
Dados: m1 = 10 kg
m2 = 20 kg
M = 50 kg
R = 0,5 m
F

R1
bloco de massa m1 vale aproximadamente, em m/s2:
V
1.82
R2
mB
PB

TCM: Teorema do centro de massa:
 Polia:
F
xi
 H  F  cos  mP  aPx

i
F
H  3600  cos60  0  H  1800N
 Fyi  V  PP  TB  F  sen  mP  aPy
1i
i
F
yi
T1 100  10  a1  T1  100 10  a1
F
2i
Peso B:

massa m2
 P2  T2  m2  a2
i
 TB  PB  mB  aB
200  T2  20  a2  T2  200  20  a2
i
TB  3000  300  aB  TB  3000  300  aB
Como não há escorregamento:
aB  R1   aB  0.6 
TB  3000  300  0.6   TB  3000 180 
TMA: Teorema do Momento Angular
 M Fi  IO 
i
 T1  P1  m1  a1
i
V  6000  TB  3600  sen60  0  V  9117.69  TB

TCM: Teorema do centro de massa:
 massa m1
O
F  R2  TB  R1  mP  k 
2

TMA: Teorema do Momento Angular
 M Fi  IO 
O
i
Polia:
a1
a2
T1
T2
3600 1.2  TB  0.6   600  0.9  
2
486
4320  TB  0.6  486 
4320  TB  0.6  486 
4320   3000  180     0.6  486  
4320 1800 108   486 
2520
2520 108    486     
594
rad
  4.24 2
s
aB  0.6   aB  2.544
m
s2
TB  3000  180    TB  3763.2 N
4.24
V  9117.69  TB  V  12880.89 N
3763.2
18. http://adm.online.unip.br/frmConsultaExercicio.aspx
Os blocos ilustrados a seguir têm massas m1 e m2. A
massa da polia é M e seu raio é R. Desprezar a massa
da corda e admitir que não há escorregamento entre
a corda e a polia. Considere a aceleração da
gravidade local igual a 10 m/s2. A aceleração do
13
P2
P1
T1  R  T2  R  I    
M  R2

2
M  R2 a

T1  T2   R  
2
R
T1  T2   R  
50
M
T1  T2    a
2
100  10  a   200  20  a   25  a
100 10  a  200  20  a  25 a
30  a  100  25  a  a 
100
m
 a  1.82 2
55
s
19. http://adm.online.unip.br/frmConsultaExercicio.aspx
Uma polia dupla, composta por dois discos
solidários entre si, possui momento de inércia total
ICM = 0,30 kg.m2, é acionada a partir do repouso, por
blocos de massas m1 = 1,5 kg, m2 = 2,5 kg, raios R1
= 0,4 m e R2 = 0,7 m, ligados a fios ideais que não
escorregam em relação a polia. Desprezar atritos,
adotar g = 10 m/s2. A tração no fio que sustenta a
Notas de Aula 2 – Dinâmica dos Sólidos – Prof. Dr. Cláudio S. Sartori
massa m2, expressa em N, é aproximadamente:
25.35
F
f
HB
Sentido de giro:
P1  R2  P2  R1  0  P1 
R1
P2
R2
HA
VA N N
0.7
P1 
25  P1  43.75N  15N  horário
0.4
TCM: Teorema do centro de massa:
 massa m1
 F1i  T1  P1  m1  a1  a1  R2 
PA

T1 15  15  0.7   T1  15 1.05 

massa m2
 F2i  P2  T2  m2  a2  a2  R1 
F
i
 VA  F  f  PA  mA  ayA
yi

Engrenagem B
 Fxi  HB  N  mB  axB
i
 Fyi  VB  f  PB  mB  ayB
0.4
O
i
i
25  T2  2.5  R1    T2  25  1 
TMA: Teorema do Momento Angular
 M Fi  IO 
 H A  N  mA  axA
xi
i

i

TMA: Teorema do Momento Angular
M
Polia:
T1  R2  T2  R1  I G    
i
T1  0.7  T2  0.4  0.3
 0.735  0.4  0.3    10  10.5
Engrenagem A:

Engrenagem B:
T2  25  1   T2  25  1  0.3483
F
14
f  rB  I B   B
f  0.1  0.8   B
0.5
rad
   0.3484 2
1.435
s
20. (Livro Unip pg. 89 3.13) - Duas engrenagens
A e B, possuem eixos fixos paralelos, conforme
ilustrado. Soldada coaxialmente ‘a engrenagem A,
uma polia de raio 0.05m é acionada pela força F =
500 N, através de um fio enrolado na mesma. As
engrenagens A e B, possuem, respectivamente, rA =
0.3 m e rB = 0.1 m; os momentos de inércia da
engrenagem A e da polia soldada é IA = 1.2 kg.m2;
o momento de inércia da polia B é IB = 0.8 kg.m2.
Os atritos são desprezíveis. Pedem-se:
(a) a aceleração angular da engrenagem A;
(b) a aceleração angular da engrenagem B;
(c) a força que a engrenagem A aplica na
engrenagem B.
 IO  
f  rA  F  r  I A   A
f  0.3  500  0.05  1.2  A
f  0.3  25  1.2   A
10.5  0.735 10  0.4   0.3
T2  25.3483N
FiO

15  1.05     0.7   25  1    0.4  0.3  
1.435   0.5    
PB
TCM: Teorema do centro de massa:
Engrenagem A
F
i
f
VB
f 

0.8
 B  f  8  B
0.1
Ponto de engrenamento:
vA  vB  A  rA  B  rB
aTA  aTB  A  rA  B  rB
r
0.3
 B   A  A   B    A   B  3   A
rB
0.1
f  8 B  f  24   A
24  A  0.3  25  1.2   A  7.2   A  25  1.2   A
25  7.2   A 1.2   A  25  8.4   A
A  
25
rad
  A  2.97 2
8.4
s
 B  3   A   B  3   2.97    B  8.91
f  8   B  f  71.28 N
8.91
rad
s2
Notas de Aula 2 – Dinâmica dos Sólidos – Prof. Dr. Cláudio S. Sartori
21. (Livro Unip pg. 115 3.35) - A figura ilustra
um cilindro homogêneo, de massa m = 5.0 kg, raio
R = 0.33 m, que abandonado do repouso, apoiado
em plano inclinado de ângulo  = 30° com a
horizontal, rola sem escorregar ao longo do mesmo.
Pedem-se:
(a) a aceleração do centro de massa;
(b) o mínimo valor do coeficiente de atrito
entre o cilindro e o plano inclinado.
25   5  2.5   a
25  7.5  a  a 
25
m
 a  3.333 2
7.5
s
a    R    
a
R
3.333
rad
   10.1 2
0.33
s
m a
5  3.333
f 
f 
 f  8.3325N
2
2
 
fat    N
f
8.3325
  at   
   0.19
N
43.3

y
x
N
f at
22. Um aro de 10 lb ou um anel fino é dada
uma velocidade angular inicial 0 = 6 rad/s quando
é colocado sobre a superfície. Se o coeficiente de
atrito cinético entre o aro e a superfície é k = 0.3
determinar a distância que o aro se desloca antes de
parar o escorregamento.
Dados: g = 32.2 ft/s2; 1 in = 1/12 ft
I = m r2
P
  300

F
TCM: Teorema do centro de massa:
xi
i

P  sen300  f at  m  a
m g  510
F
yi
0.5
25  fat  5  a
 N  P  cos300  0
i
N  P  cos 300  N  50  cos 300

TCM: Teorema do centro de massa:
F
43.3 N
xi
 Fat  m   aG 
i

TMA: Teorema do Momento Angular
M
i
FiO
 IO  
 K  N  m  a   K W  m  a  a   K  g
9.66 ft / s 2
F
Cilindro:
m  R2
 f R 

2
m R
f 
   a  aT    R
2
m R
f 
   a    R
2
f 
25 
15
m R  a 
ma
    f 
2  R
2
m a
5 a
 5  a  25 
 5 a
2
2
yi
 N W  0  N  W
i

TMA: Teorema do Momento Angular
M
i
FiO
 IO  
Aro:
Fat  r  m  r 2   k  m g  r  m r 2 
 
k  g
0.3  32.2
0.5
rad
  19.32 2
s
r
  
Quando parar o escorregamento:
Notas de Aula 2 – Dinâmica dos Sólidos – Prof. Dr. Cláudio S. Sartori
vG    r
0  r
aG  t  0    t   r  t 
aG    r

6  0.5
t
 t  0.1553s
9.66   19.32  0.5
F
xi
  0    t    6 19.32  0.1553
 3
R1
`
TCM: Teorema do centro de massa:
Engrenagem A
 m  aG  22.5  5  aG  aG 
i
4.5m s 2
F
rad
s
yi
 N  P  0  N  P  50N
i
 2  02
32  62
 
  
2 
2   19.32 

TMA: Teorema do Momento Angular
M
i
s  r    s  0.116 ft
23. (Livro Unip pg. 115 3.36) - A figura ilustra
um carretel de massa 5 kg, raio de giração k = 0.09
m e raios R1 = 0.08 m e R2 = 0.16 m que é acionado
por uma força F = 22.5 N, aplicada por uma corda
enrolada no mesmo e que não escorrega. O carretel
apoia-se em superfície horizontal, com coeficiente
de atrito estático e cinético, respectivamente, e =
0.30 e c = 0.25. Pedem-se:
(a) determinar se ocorre ou não
escorregamento;
(b) a aceleração angular do carretel.
22.5
5

FiO
 IO  
Carretel:
F  R1  IG   22.5 0.08  5 0.092 

1.8
0.0405
44.44 rad s 2
Da cinemática dos sólidos:
aP  aG     P  G        P  G  
Onde P é o ponto de contato do carretel
com o piso. Lembrando que  = 0:

aP  4.5  iˆ  44.4  kˆ   R2  ˆj

aP  4.5  iˆ  R2  44.4  kˆ  ˆj
0.12
 iˆ
aP  4.5  iˆ  5.33  iˆ  aP  9.83  iˆ
Ou seja, o ponto P se desloca para a direita;
a força de atrito apontará para a esquerda:
R2
`
F
R1
F
N
P
R2
`
R1

F
TCM: Teorema do centro de massa:
Engrenagem A
F
xi
 m  aG  F  Fat  m  aG
i
Supondo ausência de atrito:
F
yi
22.5  Fat  5  aG
 N  P  0  N  P  50N
i

R2
16
TMA: Teorema do Momento Angular
M
i
F
FiO
 IO  
Notas de Aula 2 – Dinâmica dos Sólidos – Prof. Dr. Cláudio S. Sartori
F  R1  Fat  R2  I O    
22.5  0.08  Fat  0.12  5  0.092    
1.8  0.12  Fat  0.0405  
Como não há escorregamento: o CIR é o
ponto de contato do carretel com o solo:
aG  R2   aG  0.12 
22.5  Fat  5  aG  22.5  Fat  0.6  
0.12
22.5  Fat  0.6  


1.8  0.12  Fat  0.0405  
F
R2
22.5   0.12   1.8  0.6   0.12     0.0405  
0.9  0.1125     
0.9
0.1125
R1
`
rad
s2
Supondo ausência de atrito:
22.5  Fat  0.6  8  Fat  22.5  4.8  Fat  17.7N
 8
15 N
Como
F
0  Fat  e  N
R2
0.350
A força de atrito é maior que a máxima
permitida; portanto, a hipótese que não escorrega é
falsa; logo a relação aG  R2   aG  0.12  
R1
P
`
N
não vale; Assim, teremos que calcular a força de
12.5 N
atrito cinética:
Fat  e  N
0.2550
10

22.5  12.5  5  aG  aG 

5

m
2 2


s

1.8  0.12 12.5  0.0405       0.3

0.405

rad
7.48 2

s

Ou seja, o centro de massa está acelerando
para direita com aceleração de 2 m/s2 e está girando
no sentido horário.
Como a força F é menor que o peso, CM
não se desloca na vertical; como, adotando a força
de atrito Fat nula e  = 0, não tendo forças na
horizontal, teremos:
 TCM: Teorema do centro de massa:
F
xi
F
yi
i

 m  aG  aG  0
i
 F  N  P  0  N  30N
20
50
TMA: Teorema do Momento Angular
M
i

FiO
 IO  
Carretel:
F  R1  IG   20  0.08  5 0.092 

24. (Livro Unip pg. 115 3.37) - A figura ilustra
um carretel de massa 5 kg, raio de giração k = 0.09
m e raios R1 = 0.08 m e R2 = 0.16 m que é acionado
por uma força F = 20 N, aplicada por uma corda
enrolada no mesmo e que não escorrega. O carretel
apoia-se em superfície horizontal, com coeficiente
de atrito estático e cinético, respectivamente, e =
0.30 e c = 0.20. Pedem-se:
(a) a aceleração angular do carretel;
(b) a aceleração do centro de massa.
17
1.6
0.0405
39.51rad s 2
Da cinemática dos sólidos:
aP  aG     P  G        P  G  
Onde P é o ponto de contato do carretel
com o piso. Lembrando que  = 0:

aP  0  39.51  kˆ   R2  ˆj

Notas de Aula 2 – Dinâmica dos Sólidos – Prof. Dr. Cláudio S. Sartori
aP   R2  39.51  kˆ  ˆj
m
aP  6.32  iˆ 2
s
Ou seja, o ponto P se desloca para a direita;
a força de atrito apontará para a esquerda:
F
R2
`
R1
F
aG  0.16  9.52  aG  1.52
 iˆ
0.12
N
m
s2
25. (Livro Unip pg. 134 3.50) - A figura ilustra
um carretel de massa 6 kg, raio de giração k = 0.13
m e raios R1 = 0.08 m e R2 = 0.16 m que é acionado
por uma força F = 20 N, aplicada por uma corda
enrolada no mesmo e que não escorrega. O carretel
apoia-se em superfície horizontal, com coeficiente
de atrito estático e cinético, respectivamente, e =
0.20 e c = 0.15. Pedem-se:
(a) determinar se ocorre ou não
escorregamento;
(b) a aceleração angular do carretel.
(c) a aceleração do centro de
massacarretel.
P

F
xi
i
TCM: Teorema do centro de massa:
Carretel:
 m  aG  Fat  m   aG   Fat  5  aG
F
 F  N  P  0  N  30N
yi
i

TMA: Teorema do Momento Angular
M
i
FiO
 IO  
R2
F  R1  Fat  R2  IO  
20  0.08  Fat  0.16  5 0.092 
F
R1
`
1.6  0.16  Fat  0.0405  
Hipótese 1: não há escorregamento:
aG  R2   aG  0.16 
Supondo ausência de atrito:
1.6  0.16  Fat  0.0405    1.6  0.128    0.04  
5016

1.6
rad
   9.52 2
0.128  0.04
s
R2
0.168
Fat  5  aG  Fat  0.8    Fat  7.61N
9.52
0.16
F
R1
`
Para não haver escorregamento:
9N

0  Fat  e  N
0.330
Como 7.61  Fat  e  N
E
9
A força de atrito é menor que a máxima
permitida; portanto, a hipótese que não escorrega é
verdadeira;
logo
a
relação
aG  R2   aG  0.16  vale; Assim:
rad
  9.52 2
s
18
TCM: Teorema do centro de massa:
Engrenagem A
F
xi
 m  aG  20  6  aG  aG 
i
20
6
3.33m s 2
F
yi
 N  P  0  N  P  60N
i

TMA: Teorema do Momento Angular
M
i

FiO
 IO  
Carretel:
F  R1  IG   20  0.08  6  0.132 
Notas de Aula 2 – Dinâmica dos Sólidos – Prof. Dr. Cláudio S. Sartori

20   0.16   1.6  0.96   0.16     0.1014  
1.6
0.1014
3.2 1.6  0.1536    0.1014     
15.78rad s 2
Da cinemática dos sólidos:
rad
s2
20  Fat  0.96 18.82
  18.82
aP  aG     P  G        P  G  
Onde P é o ponto de contato do carretel
com o piso. Lembrando que  = 0:

aP  3.33  iˆ  15.78  kˆ   R2  ˆj
Fat  20 18.1  Fat  1.9N

12 N
aP  3.33  iˆ  R2 15.78  kˆ  ˆj
Como
0  Fat  e  N
 iˆ
0.16
aP  3.33  iˆ  2.52  iˆ  aP  5.85  iˆ
Ou seja, o ponto P se desloca para a direita;
a força de atrito apontará para a esquerda:
1.9
0.260
A força de atrito é menor que a máxima
permitida; portanto, a hipótese que não escorrega é
verdadeira; logo a relação:
aG  R2    aG  0.16    aG  3
F
R1
F
N
P

TCM: Teorema do centro de massa:
Engrenagem A
F
xi
 m  aG  F  Fat  m  aG
i
F
yi
20  Fat  6  aG
 N  P  0  N  P  60N
26. (Livro Unip pg. 134 3.51) - A figura ilustra
um carretel de massa 6 kg, raio de giração k = 0.13
m e raios R1 = 0.08 m e R2 = 0.16 m que é acionado
por uma força F = 20 N, aplicada por uma corda
enrolada no mesmo e que não escorrega. O carretel
apoia-se em superfície horizontal, com coeficiente
de atrito estático e cinético, respectivamente, e =
0.20 e c = 0.15. Pedem-se:
(a) determinar se ocorre ou não
escorregamento;
(b) a aceleração angular do carretel.
(c) a aceleração do centro de
massacarretel.
i

TMA: Teorema do Momento Angular
M
i
FiO
 IO  
 F  R1  Fat  R2  I O    
20  0.08  Fat  0.16  6  0.132    
1.6  0.16  Fat  0.1014  
Hipótese: se não houver escorregamento:
12 N
0  Fat  e  N
R2
0.260
o CIR é o ponto de contato do carretel com o solo:
aG  R2   aG  0.16 
`
R1
20  Fat  6  aG  20  Fat  0.96  
0.16
20  Fat  0.96  


1.6  0.16  Fat  0.1014  
19
m
s2
Ou seja, o centro de massa está acelerando
para direita com aceleração de 3 m/s2 e está girando
no sentido horário.
R2
`
4.8
0.255
Supondo ausência de atrito:
F
Notas de Aula 2 – Dinâmica dos Sólidos – Prof. Dr. Cláudio S. Sartori
F  R1  Fat  R2  I O    
20  0.08  Fat  0.16  6  0.132 
R2
1.6  0.16  Fat  0.1014  
F
R1
`

Hipótese: se não houver escorregamento:
12 N
TCM: Teorema do centro de massa:
Engrenagem A
F
xi
20
6
 m  aG  20  6  aG  aG 
i
3.33m s 2
F
yi
 N  P  0  N  P  60N
i

TMA: Teorema do Momento Angular
M
i

FiO
 IO  
1.6
0.1014
15.78rad s 2
Da cinemática dos sólidos:
aP  aG     P  G        P  G  
Onde P é o ponto de contato do carretel
com o piso. Lembrando que  = 0:

aP  3.33  iˆ  15.78  kˆ   R2  ˆj

aP  3.33  iˆ  R2 15.78  kˆ  ˆj
 iˆ
0.16
aP  3.33  iˆ  2.52  iˆ  aP  0.81 iˆ
Ou seja, o ponto P se desloca para a direita;
a força de atrito apontará para a esquerda:
R2
F
R1
F
N
P

TCM: Teorema do centro de massa:
Engrenagem A
F
xi
 m  aG  F  Fat  m  aG
i
F
yi
20  Fat  6  aG
 N  P  0  N  P  60N
i

TMA: Teorema do Momento Angular
M
i
20
FiO
 IO  
aG  R2   aG  0.16 
20  Fat  6  aG  20  Fat  0.96  
0.16
20  Fat  0.96  


1.6  0.16  Fat  0.1014  
3.2  1.6  0.1536    0.1014     
F  R1  IG   20  0.08  6  0.132 
`
0.260
o CIR é o ponto de contato do carretel com o solo:
20   0.16   1.6  0.96   0.16     0.1014  
Carretel:
 
0  Fat  e  N
1.6
0.255
rad
s2
20  Fat  0.96  6.27
  6.27
Fat  20  6.02  Fat  13.98N
12 N
Como
0  Fat  e  N
0.260
A força de atrito é maior que a máxima
permitida; portanto, a hipótese que não escorrega é
falsa; logo a relação:
aG  R2  não é valida.
Assim, haverá escorregamento e:
Fat  c  N  Fat  0.15  60  Fat  9N
20  Fat  6  aG


9

1.6  0.16  Fat  0.1014  
9

11
m

aG   aG  1.83 2


6
s

0.16
rad
  
   1.58 2

0.1014
s

Ou seja, o centro de massa está acelerando
para direita com aceleração de 1.83 m/s2 e está
girando no sentido horário com aceleração angular
1.58 rad/s2.
Notas de Aula 2 – Dinâmica dos Sólidos – Prof. Dr. Cláudio S. Sartori
 Movimento combinado de rotação e
translação: Relações envolvendo energia.
Todo movimento de um corpo rígido pode
ser sempre dividido em um movimento de
translação do centro de massa e outro de rotação em
torno do centro de massa. A energia cinética do
corpo possui duas parcelas: uma devida à translação
do centro de massa e outra devida à rotação:
K

1
1
2
M  vcm
 I cm   2
2
2
Condição
para
deslizamento:
vCM  R  
21
rolamento
sem
Notas de Aula 2 – Dinâmica dos Sólidos – Prof. Dr. Cláudio S. Sartori
K2 
1
1 1
v 
2
M  vcm
  M  R 2   CM 
2
2 2
 R 
3
2
K2  M  vcm
4
2
Aplicando a conservação da energia:
K1  U1  K2  U2
3
2
0  M  g  h  M  vcm
0
4
4
vcm 
g h
3
 Exemplo 3 – Competição entre corpos
girando. Em uma demosntração durante a aula de
física, o professor faz uma “competição” de vários
corpos rígidos redondos, deixando-os rolar do alto
de um plano inclinado. Qual a forma do corpo que
alcança primeiro a parte inferior?
 Exemplo 1 – Enrolamento de uma casca
cilíndrica. Uma casca cilíndrica oca de raio R e
massa M rola sem deslizar com uma velocidade vCM
ao longo de uma superfície plana. Qual a sua
energia cinética?

Solução:
1
1
2
M  vcm
 I cm   2
2
2
2
1
1
v 
2
K  M  vcm
  M  R 2    CM 
2
2
 R 
2
K  M  vcm
K
 Exemplo 2 – Velocidade de um ioiô. Um
ioiô é feito enrolando-se um fio diversas vezes em
torno de um cilindro de massa M e raio R. Mantémse presa a extremidade enquanto o cilindro é
liberado sem velocidade inicial. O fio se desenrola,
mas não desliza nem se dilata à medida que o
cilindro cai e gira. Use considerações de energia
para achar a velocidade do centro de massa vCM do
cilindro sólido depois que ele caiu a uma distância
h.
 Solução:
K1  0  U1  M  g  h  U2  0
1
1
2
K2  M  vcm
 I cm   2
2
2
K1  U1  K2  U2
1
1
2
0  M  g  h  M  vcm
 I cm   2  0
2
2
Chamando de:
Icm  c  M  R2
1
1
v 
2
M  g  h  M  vcm
 c  M  R 2   cm 
2
2
 R 
1
1
2
2
M  g  h  M  vcm
 M  vcm
c
2
2
2
1
2 gh
2
M  g  h  M  vcm
1  c   vcm 
2
1 c
 Solução:
1
1
2
M  vcm
 I cm   2
2
2
vCM
1

 I  M  R2
R
2
K
22
Todos os cilindros sólidos possuem a
mesma velocidade no ponto inferior do plano,
mesmo quando possuem massas e raios diferentes,
pois eles possuem o mesmo valor da constante c.
Todas as esferas sólidas possuem a mesma
velocidade na base do plano. Quando menor o valor
de c maior a velocidade do corpo quando ele chega
Notas de Aula 2 – Dinâmica dos Sólidos – Prof. Dr. Cláudio S. Sartori
na parte inferior do plano. Observando a tabela de
momento de inércia, vemos que a ordem de chegada
do plano é: Qualquer esfera maciça, qualquer
cilindro maciço, qualquer esfera oca com parede
fina ou casca esférica e, finalmente, qualquer casca
cilíndrica.
M g 
 Exemplo 4 – Aceleração de um ioiô.
Ache a aceleração de cima para baixo do ioiô e a
tensão no fio.
3
2
M  acm  acm  g
2
3
1
T  M  acm
2
1
2
T  M g
2
3
2
T  M g
3
 Exemplo 5 – Aceleração de uma esfera
rolando. Uma esfera de bliche sólida rola sem
deslizar para baixo de uma rampa ao longo de uma
guia. O ângulo de inclinação da rampa em relação à
horizontal é . Qual é a aceleração da bola?
Considere a bola uma esfera homogênea sólida,
desprezando seus orifícios.
 Solução:
A equação para o movimento de translação
do centro de massa é:
F
y
 M  g  T  M  acm
O momento de inércia em relação a um
eixo que passa pelo centro de massa:
I
1
M  R2
2
Somente a força de tensão possui torque
em relação a um eixo que passa pelo centro de
massa é:
  T  R  I
cm
  T  R 
1
M  R2  
2
Como o fio se desenrola sem se deslizar:
vCM  R  
aCM
a
 R      CM
R
1
T  M  R 
2
acm
1
M  acm
2
M  g  T  M  acm
1
M  g  M  acm  M  acm
2
1
M  g  M  acm  M  acm
2
T
23
 Solução:
A figura mostra o diagrama de corpo livre,
mostrando o sentido positivo das coordenadas.
Usando o momento de inércia da esfera
sólida:
I
2
M  R2
5
Equações de translação e rotação do centro
de massa e chamando de f a força de atrito:
F
x
 M  g  sen  f  M  acm
  f  R  I
cm
Como: aCM
2
M  R2  
5
a
 R      CM
R
  f  R 
Substituindo, teremos:
2
M  acm
5
M  g  sen  f  M  acm
2
M  g  sen  M  acm  M  acm
5
2
M  g  sen  M  acm  M  acm
5
f 
Notas de Aula 2 – Dinâmica dos Sólidos – Prof. Dr. Cláudio S. Sartori
M  g  sen 
f 
7
5
M  acm  acm   g  sen
5
7
2
2
5
M  acm  f  M   g  sen
5
5
7
2
f   M  g  sen
7
Coeficiente de atrito:
 Exemplo 6 – Um anúncio fazendo
propaganda da potência desenvolvida pelo motor de
um automóvel afirma que o motor desenvolve
1.49.105W para uma rotação de 6000 rpm. Qual é o
torque desenvolvido pelo motor?

Solução:
2
 M  g  sen
f
7
 
N
M  g  cos 
2
  tg 
7
 Trabalho e potência no movimento de
rotação
Podemos escrever:
P      
f  100Hz
  2  f    2 100    200
2
  237N  m
1
Podemos desenvolver:
dW  I    d  dW  I 
d
 d
dt
dW  I   d
d
 d
dt
dW  I 
W
 Exemplo 7 Um motor elétrico
desenvolve um torque constante de  = 10 N.m
sobre o esmeril montado no seu eixo motor. O
momento de inércia é I = 2.0 kg.m². Sabendo que o
sistema começa a se mover a partir do repouso,
calcule o trabalho realizado pelo motor em 8.0 s e a
energia cinética no instante final. Qual a potência
média desenvolvida pelo motor?
 Solução:
2
 I    d
1
1
1
I  22  I  12
2
2
dW
d
 
dt
dt
P   
Wtot 
rad
s
1.49 105

200
dW    d
dW    d

6000
f  6000rpm 
Hz
60
dW  Ftan ds  ds  R  d
dW  Ftan R  d
W     d
P
  I    

I
10
rad
    2
2
s
   t
rad
  5  8    40
s
1
1
K  I   2  K  2  402  K  1600 J
2
2
1
1
    t 2    5  82    160rad
2
2
W    W  10 160 W  1600J
P
W
1600
P
 P  200W
t
8
A potência instantânea P =  não é constante,
porque  cresce continuamente. Porém podemos
calcular o trabalho total por:
t2
t2
t1
t1
W   P  dt  W       dt
24
Notas de Aula 2 – Dinâmica dos Sólidos – Prof. Dr. Cláudio S. Sartori
t2
8
W       t  dt   10  5  tdt
t1
0
W  50
2 t 8
t
2
dL

dt
 W  1600 J
t 0
 Momento angular e energia de rotação
Lembremos que uma grandeza análoga ao
momento linear
p
de uma partícula é o momento
angular, que representamos por
como:
L.
Definimos
Lrp
Para um corpo rígido de i partículas, o momento
angular de cada uma será:
Li  mi  vi  ri
L  m  v  r  sen
L  m v  l
Pode-se mostrar que a taxa de variação do
momento angular é igual ao torque da força
resultante:
dL dr
dp
  pr
dt dt
dt
dL dr
mdv
  mv  r 
dt dt
dt
dL
 v  mv  r  ma
dt
0
dL
 r F
dt
25
Li  mi   ri  i   ri
Li  mi  ri2  i
L   Li  L   mi  ri 2  i
L  I 
Notas de Aula 2 – Dinâmica dos Sólidos – Prof. Dr. Cláudio S. Sartori
 Exemplo 1 – A hélice da turbina de um
motor a jato possui momento de inércia 2.5 kg.m²
em torno do eixo de rotação. Quando a turbina
começa a girar, sua velocidade angular em função
do tempo é dada por
  400  t 2 rad s3 
(a) Calcule o momento angular da hélice em
função do tempo e ache seu valor em t = 3.0 s.
(b) Determine o torque resultante que atua sobre
a hélice em função do tempo e calcule seu valor para
t = 3.0 s.

(a)
Solução:
L  I    L  2.5  400  t 2
L  1000  t 2
L  t  3  1000  32  L  9000
kg  m2
s
dL
   1000  2t
dt
  2000  t
  t  3  2000  3    6000 N  m
(b)  

26
Conservação do momento angular
Notas de Aula 2 – Dinâmica dos Sólidos – Prof. Dr. Cláudio S. Sartori
Princípio da conservação do momento angular:
Esse princípio vale em todas escalas, desde o
sistema atômico como o planetário e decorre da
equação:
Quando
dL

dt
dL
i  i  0  dt  0
Podemos escrever também:
I1  1  I2  2
I
13
rad
2  1  1  2 
   2  5
I2
2.6
s
f2 
I1
13
 f1  f 2 
 0.5  f 2  2.5Hz
I2
2.6
K1 
1
1
I1  12  K1  13   2  K1  64J
2
2
K2 
1
1
2
I 2  22  K2  2.6   5   K1  320J
2
2
I1  1  I2  2
 Exemplo 2 – Qualquer um pode ser
bailarino. Um professor de física acrobata está de
pé sobre o centro de uma mesa girante, mantendo
seus braços estendidos horizontalmente com um
haltere de 5.0 kg em cada mão.
 Exemplo 3 – A figura mostra 2 discos, um
deles é o volante de um motor e o outro é um disco
ligado a um eixo de transmissão. Seus momentos de
inércia são IA e IB, respectivamente; inicialmente
eles estão girando com a mesma velocidade angular
A e B, respectivamente. A seguir empurramos os
dois discos um contra o outro aplicando forças que
atuam ao longo do eixo, de modo que sobre nenhum
dos dois discos surge torque em relação ao eixo. Os
discos permanecem unidos um contra o outro e
atingem uma velocidade angular final . Deduza
uma expressão para .
Ele está girando em torno de um eixo
vertical completando uma volta a cada 2.0 s.
Calcule a nova velocidade angular do professor
quando ele aproxima os dois halteres do seu
estômago e discuta como isso modifica a sua
energia cinética. Seu momento de inércia (sem os
halteres) é igual a 3.0 kg.m² quando seus braços
estão distendidos para fora, diminuindo para 2.2
kg.m² quando suas mãos estão próximas do seu
estômago. Os halteres estão inicialmente a uma
distância de 1.0 m do eixo e a distância final é igual
a 0.20 m. Considere o halteres como partículas.

Solução
I  I prof  Ihalteres
I1  3  2  512
I1  13kg  m2
I2  2.2  2  5 0.22
I2  2.6kg  m2
f
27
1
1
rad
 f  Hz    2 f    
T
2
s
 Solução:
O único torque que atua sobre cada disco é o
torque que cada disco exerce sobre o outro disco;
não existe nenhum torque externo. Logo o momento
angular total do sistema dos dois discos é o mesmo
antes e depois de eles serem unidos. No equilíbrio
final eles giram juntos como se constituíssem um
único corpo com momento de inércia:
I  I A  IB
A conservação do momento angular fornece:
I A  A  I B  B  I  
Notas de Aula 2 – Dinâmica dos Sólidos – Prof. Dr. Cláudio S. Sartori


I A  A  I B  B
I
I A   A  I B  B
I A  IB
velocidade de 400 m/s exatamente no canto da
porta. Calcule a velocidade angular da porta
imediatamente depois que a bala penetra na porta.
A energia cinética se conserva?
 Exemplo 4 – No exemplo anterior,
suponha que o volante A tenha massa de 2.0 kg, um
raio de 0.20 m e uma velocidade angular inicial de
200 rad/s. Calcule a velocidade angular comum
final  depois que os discos ficam em contato. A
energia cinética se conserva nesse processo?
 Solução:
1
1
I A  mA  rA2  I A  2  0.22  I A  0.040kg  m2
2
2
1
1
I B  mB  rB2  I B  4  0.12  I B  0.020kg  m2
2
2

I A   A  I B  B
I A  IB
0.04  50  0.02  200
0.04  0.02
rad
  100
s
1
1
K1  I A  A2  I B  B2
2
2
1
1
K1  0.04  502  0.02  2002
2
2
K1  450J
1
K2   I A  I B    2
2
1
K2   0.04  0.02 1002
2
K2  300J

Um terço da energia foi perdida na
“colisão angular”, o análogo rotacional de uma
colisão linear completamente inelástica. Não
deveríamos esperar conservação da energia
cinética, embora a força externa resultante e o
torque resultante sejam nulos, porque existem
forças internas não conservativas (forças de atrito)
que atuam enquanti os dois discos começam a girar
unidos e tendem a girar com uma velocidade
angular comum.
 Exemplo 5 – Momento angular em uma
ação policial. Uma porta de largura 1 m e massa de
15 kg é articulada com dobradiças em um dos lados
de modo que possa girar sem atrito em torno de um
eixo vertical. Ela inicialmente não está aberta. Um
policial dá um tiro com uma bala de 10 g e
28
 Solução:
Considere um sistema formado pela porta
juntamente com a bala em seu interior. Não existe
nenhum torque externo em torno do eixo definido
pelas dobradiças, de modo que o momento angular
em torno desse eixo deve se conservar. O momento
angular da bala é:
L  m v  l  L  0.01 400  0.5
L  2kg  m2 s
O momento angular final é:
L  I 
I  I porta  Ibala
I
I
mp  d 2
3
 mbala  l 2
15 12
 0.010  0.52
3
I  5.0025kg  m2
mv  L
L  I    
I
2
rad

   0.40
5.0025
s
A colisão entre a porta e a bala é inelástica
porque forças não conservativas atuam durante o
impacto da bala. Logo, não esperamos que haja
conservação da energia cinética. Para conferirmos,
calculamos a energia cinética inicial e final:
1
1
K1  m  v2  K1  0.010  4002
2
2
K1  800J
1
K2  I   2
2
1
K2  5.0025  0.42
2
Notas de Aula 2 – Dinâmica dos Sólidos – Prof. Dr. Cláudio S. Sartori
K2  0.40J
A energia cinética final é apenas 1/2000 da
energia cinética inicial.
 Exemplo 6 - Determinar, em cada caso,
o momento angular para as seguintes situações:
(a) um carro de 1200 kg percorre no sentido
anti-horário um círculo com 20 m de raio com
velocidade de 15 m/s.
(b) o carro mencionado desloca-se com
velocidade
v  15  m s   iˆ sobre
a reta y = y0
=20m, paralela ao eixo x.
(c) um disco, no plano xy, com raio de 20 m
e a massa de 1200 kg, girando a 0.75 rad/s em torno
do seu eixo, que coincide com o eixo z.


N

Solução:
i 1
(a) L  r  p  L  r  m  v  kˆ
(b) r  x  iˆ  y  ˆj  r  x  iˆ  y0  ˆj
p  m  v  p   p  iˆ
L  r  p  L  x  iˆ  y0  ˆj   p  iˆ

 

L  y0  p  kˆ
L  3.6 105  kg  m2 s   kˆ
L  I 
1

L   m  R 2     kˆ
2

1

L   1200  202   0.75  kˆ
2

L  1.8 105 kg  m2 s  kˆ
(c)


 Exemplo 7 - A máquina de Atwood tem
dois corpos de massa m1 e m2 ( sendo m1 maior que
m2), ligados por um cordel de massa desprezível que
passa por uma polia cujos rolamentos não oferecem
atrito. A polia é um disco uniforme, de massa M e
raio R. O cordel não escorrega na polia. Determinar
a aceleração angular da polia e a aceleração dos dois
corpos pela equação:
N

i 1
i ,ext

dL
dt
i ,ext

dL
dt
Lz  Lp  L1  L2
L  20 1200 15  kˆ  L  3.6 105  kg  m2 s   kˆ
Lz  I    m1  v  R  m2  v  R
 z,res  m1  g  R  m2  g  R
dL
 z ,res  Z
dt
d
m1  g  R  m2  g  R   I    m1  v  R  m2  v  R 
dt
m1  g  R  m2  g  R  I   m1  a  R  m2  a  R
 m1  m2   g  R 
a
1
a
M  R2    m1  m2   a  R
2
R
m1  m2
1
M  m1  m2
2
g
 Exemplo 8 – Um disco gira em torno de
um eixo sem atrito, que coincide com o respectivo
eixo de simetria, com velocidade angular inicial i,
como mostra a figura. O seu momento de inércia em
relação ao eixo é I1. Num certo instante, o disco cai
sobre o outro, de momento de inércia I2, montado
sobre o mesmo eixo. Graças ao atrito entre as duas
superfícies em contato, os dois discos atingem uma
velocidade angular comum aos dois, f. Calcular
essa velocidade angular.

29
Solução:
Solução:
Notas de Aula 2 – Dinâmica dos Sólidos – Prof. Dr. Cláudio S. Sartori
A velocidade angular final está relacionada
com a inicial pela conservação do momento
angular:
Lf  Li
 I1  I 2    f
f 
 I1  i
I1
 i
I1  I 2
 Exemplo 9 – Um carrossel com 2 m de
raio e 500 kg.m2 de momento de inércia gira em
torno de seu eixo, sem atrito, completando uma
volta a cada 5 s. Uma criança, com 25 kg, está
inicialmente no centro do carrossel e depois
caminha até a borda. Calcular a velocidade angular
que terá, então, o carrossel.
 Solução:
Pela conservação do momento angular:
Momento angular inicial da criança correndo
em relação ao centro da plataforma do carrossel:
Li  m  v  R
Expressão do momento angular final do sistema
criança-carrossel em termos da velocidade angular
final f:
Lf   m  r 2  Im    f
Igualando as expressões:
m R
Lf  Li
2
 Im    f  m  v  R
f 
mv R
m  R2  Im
 f  0.208
rad
s
 Exemplo 11 – Uma partícula de massa m
descreve, com velocidade v0, um círculo de raio r0
sobre a superfície de uma mesa horizontal sem
atrito. A partícula está presa a um fio que passa por
um buraco na mesa, no centro do círculo. O fio é
lentamente puxado para baixo, de modo que a
partícula acaba descrevendo um círculo de raio rf.
L f  Li
I sis, f   f  Isis,i  i
Isis  Im  Ic  Im  m  r 2
I
m
 m  R2    f  I m  i
f 
Im
 i
I m  m  R2
500
 i
500  25  22
5
 f   i
6
5 1
1 rev
f    f 
6 5
6 s
f 
 Exemplo 10 – A criança mencionada no
exemplo anterior corre com velocidade 2.5 m/s
sobre uma tangente à beira da plataforma do
carrossel, que está imóvel, e pula para a plataforma.
Calcular a velocidade angular final da criança no
carrossel.
(a) Calcular a velocidade final em termos de r0,
v0 e rf.
(b) Calcular a tensão T no fio quando a partícula
descreve um círculo de raio rf em termos de m, r e
do momento angular L0  m  v0  r0 .
(c) Calcule o trabalho feito pela partícula pela
tensão T, integrando T  dr de r0 até rf. Dar a
resposta em termos de r0, rf e L0.
 Solução:
(a) A conservação do momento angular
relaciona as velocidades final à inicial e os raios
inicial e final:
L f  L0

30
Solução:
m  v f  rf  m  v0  r0  v f 
r0
 v0
rf
Notas de Aula 2 – Dinâmica dos Sólidos – Prof. Dr. Cláudio S. Sartori
(b) Como
 F  ma
 Solução:
1.
Energia cinética depois da colisão em
termos do momento angular Li e do momento de
inércia I´do sistema bola-massa:
i
i
T  m
v2
r
m v f  rf  m v0  r0  L0
L
v 0
mr
2
 L0 


v2
mr 

T  m  T  m
r
r
L2
T 03
mr
Ef 
L f  Li  L f  Li  m  v  x
3.
Ef 
rf
L20
L20
dW  
 dr  W   
 dr
m  r3
m  r3
r0
W
2
0
L
2 m  r2
r  rf
As expressões de Lf e de I´na equação de Ef
ficam:
L2f
2 I
 Ef 
1


2   m  x2  M  d 2 
3


2
2
2

3  m v  x
Ef  
2
2 
2  3m  x  M  d 
Exercícios de Revisão:
1. O rotor de um motor elétrico tem uma
freqüência de 3600 rpm , quando a carga e a energia
são cortadas. O rotor de 50 kg , que tem um raio de
giração do centro de gravidade de 180 mm , então
começa a parar . Sabendo que a cinética de fricção
devido ao atrito corresponde a um torque de
magnitude 3,5 N ⋅ m exercida sobre o rotor ,
determinar o número de revoluções que o rotor
executa antes de vir a parar.
n

31
2
3  m2  v2  x2 


Ef
2  3m  x 2  M  d 2 

1
Ei
m  v2
2
Ef
3m  x2

Ei 3m  x2  M  d 2
L20  1 1 
W
  
2  m  rf2 r02 
Achar a razão entre a energia final e a energia
inicial do sistema.
m  v  x
5.
A razão entre a energia cinética depois da
colisão e a energia inicial da bola de massa plástica
é então:
r  r0
 Exemplo 12 – Uma barra de massa M e
comprimento d pode girar em torno de um eixo fixo
a uma de suas extremidades. Uma bola de massa
plástica, com massa m e velocidade v, atinge a barra
a uma distância x do eixo e fica grudada na barra.
O momento de inércia I´:
1
I   m  x2  M  d 2
3
(c) O trabalho é:
L2
Tr  0 3
mr
2 I
2.
Conservação do momento angular para
relacionar Li a m, v e x:
4.
dW  T  dr  dW  Tr  dr
L2f
Solução:

i 1
Fi ,O
 IO 
Notas de Aula 2 – Dinâmica dos Sólidos – Prof. Dr. Cláudio S. Sartori
IO  m kO2  IO  50  0.182  IO  1.62kg  m2
rad
3.5  1.62      2.16 2
s
f0  3600rpm  60Hz
rad
0  2  60  0  376.991
s
rad
0  2  60  0  376.991
s
 2  02  2       
 
0.3
P
z

Posição do centro de massa:
L
1 0  1
m1  x1  m2  x2
2
xG 

m1  m2
2
L
xG   xG  0.075m
4
 2  02
2 
02  376.9912
   32891.067rad
2  2.16
n
A
zG 
 32891.067

 n  5234.77
2
2 
zG 
m1  z1  m2  z2
m1  m2
1 0.15  1 0
 zG  0.075m
2
d  xG2  yG2  d  0.0752  0.0752
2. B.J. Cap.16.54 - Uma barra em forma
de L delgada uniforme ABC está em repouso em
uma superfície horizontal quando uma força de
magnitude P = 4 N é aplicada no ponto A.
Desprezando o atrito entre o barra e a superfície e
sabendo que a massa do conjunto de barras idênticas
é de 2 kg , determine:
(a) a aceleração angular inicial da barra;
(b) a aceleração inicial do ponto B.
d  0.106m
Utilizando o Teorema de Steiner para as
duas barras e somando:
m
m
m
m
I G  2 L2  xG2  2 L2  zG2
12
2
12
2
2
2
2
2
I G  2 0.32  d 2  2 0.32  d 2
12
2
12
2
2
IG  2  0.0075  0.106  IG  0.037472kg  m2



n

i 1
Fi ,G
TMA
 IG 
0.3
0.037472
rad
rad
  8 2    8  j 2
s
s
4  0.075  0.037472      
i
j
xG
B

x
yG
d
d
0.15
0.3
G
n
i 1
i 1
 Fiz  m  az   Fix  m  ax
4  k  2  a  aGz  2  k
L/2=0.15
32
TCM:
n
r  GB  B  G
Notas de Aula 2 – Dinâmica dos Sólidos – Prof. Dr. Cláudio S. Sartori
aB  aG    r    v


aB  2  k  8  j  0.075  i  0.075  k  0
 
aB  2  k  0.6  k  0.6  i
aB  2  k  0.6  k  0.6  i
m
aB  0.6  i  2.6  k  2 
s 
3. A polia dupla composta por duas
polias de raios R1 = 0.20 m e R2 = 0.50 m,
rigidamente soldadas entre si com eixo fixo,
em relação ao qual o momento de inércia é I =
0.9 kg.m2. O acionamento da polia dupla é feito
a partir do repouso, por blocos de massas m1 =
25 kg e m2 = 12 kg, ligados a fios ideais que
não escorregam em relação a mesma. A
aceleração linear do bloco 2, expressa em m/s2,
é aproximadamente:
T1  R2  T2  R1  IG  
T1  0.5  T2  0.2  0.9  
a1    R2
 a  0.5  
 1

a2    R1
a2  0.2  
250  T1  25  0.5  
T  251  12.5  
 1

T2  120  12  0.2  
 T2  120  2.4  
 250  12.5     0.5  120  2.4     0.2  0.9  
125  6.25    24  0.48    0.9  
6.25    0.48    0.9    24 125
101
rad
7.63    101   
   13.23 2
7.63
s
m

 a1  6.62 s 2
 a1  0.5  13.23


a2  0.2  13.23
a  2.65 m
 2
s2
T1  251  12.5  13.23
 T  85.63N
 1

 T2  120  2.4  13.23
T2  151.75 N
4. A velocidade angular da polia dupla
após 5 s, expressa em rad/s, é
aproximadamente:
  0    t    0  13.23  5
  0    t    66.15
rad
s
5. A velocidade do bloco 1 após 5 s,
expressa em rad/s, é aproximadamente:

v1    R2  v1  66.15  0.5  v1  33.075
TCM:
 P  T  m1  a1
Fi  m  a   1 1

i 1
T2  P2  m2  a2
n
250  T1  25  a1

T2  120  12  a2

n

i 1
33
Fi ,G
TMA
 IG 
6. Os blocos ilustrados a seguir têm massas
m1 e m2. A massa da polia é M e seu raio é R.
Desprezar a massa da corda e admitir que não há
escorregamento entre a corda e a polia. Considere a
aceleração da gravidade local igual a 10 m/s2. A
aceleração do bloco de massa m1 vale
aproximadamente, em m/s2:
m
s
Notas de Aula 2 – Dinâmica dos Sólidos – Prof. Dr. Cláudio S. Sartori
barra tem zero de aceleração.
Dados: m1 = 10 kg m2 = 20 kg
M = 50 kg R = 0.5 m

TCM: Teorema do centro de massa:
 massa m1
F
1i
 T1  P1  m1  a1
i
T1 100  10  a1  T1  100 10  a1
F
2i

massa m2
W
m  L2
W  L2
m   IG 
 IG 
g
12
12 g
 P2  T2  m2  a2
i
200  T2  20  a2  T2  200  20  a2

TMA: Teorema do Momento Angular
M
i
FiO

a
a2
T1
T2
F
xi
T1  R  T2  R  I    
M  R2

2
2
M R a

T1  T2   R  
2
R
T1  T2   R  

TMA:
M
M
a
2
100  10  a   200  20  a   25  a
100 10  a  200  20 a  25 a
30  a  100  25  a  a 
100
m
 a  1.82 2
55
s
A haste delgada uniforme AB
repousa sobre uma superfície horizontal
sem atrito, e uma força de magnitude Q =
0.25 lb é aplicado a uma numa direção
perpendicular à haste. Sabendo-se que a
haste pesa 1.75 lb, determinar
(a) a aceleração do ponto A,
(b) a aceleração ponto B,
(c) a localização do ponto em que a
7.
34
FiO
L W  L2
Qg

    6
2
12 g
W L
 6
0.25 g
6g
 
1.75 L
7L
6g
 
j
7L

a A  aG  AG        AG
AG 
50
T1  T2  
1
g i
7
 IO  
aG 
Q
P2
W
a
g
Q g
0.25
1
a
g  aG  g
W
1.75
7
i
P1
 m  aG  Q 
i
 IO  
Polia:
a1
TCM:
aA 

L
k
2
1
L
6g
g i  k 
j
7
2
7L
1
3
g i  g i
7
7
4
4
aA  g  i  aA  32.2  i
7
7
aA 
m
aA  18.4  i  2  
s 

aB  aG  BG        BG

Notas de Aula 2 – Dinâmica dos Sólidos – Prof. Dr. Cláudio S. Sartori
BG  
L
k
2
1
L
6g
g i  k 
j
7
2
7L
1
3
aB  g  i  g  i
7
7
2
2
aB   g  i  aA   32.2  i
7
7
aB 
m
aB  9.2  i  2  
s 


aP  aG  PG        PG  0
1
6g
L

g i    zk  
 j0
7
7L
2

1
6 gL

g i 
  zi  0
7
7 L 2

1
6 gL

g
  z  0
7
7 L 2

6 gL 
1
  z   g
7 L 2
7


Haste ABC em equilíbrio:
TMA:
M
i
FiA
0
RAv
R Ah
L
1
L L
z Lz 
2
6
2 6
3L L
2L
z
 z
6 6
3
N
Fat
 N  10  Fat  8  6   P  15  6   0
 N 10  Fat  2  75  9  0
 N  10    N  2  675  0
N 10  0.35  N  2  675  0
10  N  0.7  N  675  0  9.3 N  675
N
675
 N  72.58N
9.3
Fat    N  Fat  0.35  72.58
Fat  25.4 N

8. (Beer & Johnston 16.27 10ª Ed.) O
tambor de 8 in de raio está ligado a um volante maior. O
momento de inércia total do tambor e o volante é de 14
lb.ft2 e o coeficiente de atrito cinético entre o tambor e a
sapata de freio é de 0.35. Sabendo-se que a velocidade
angular do volante é de 360 rpm sentido anti-horário
quando uma força P de grandeza de 75 lb é aplicada ao
pedal de C, determinar o número de revoluções realizadas
pelo volante até atingir o repouso.
35
TMA:
M
i
FiD
 IO  
r  Fat  IO  
r  Fat
rN
 
IO
IO
r  Fat
rN

 
IO
IO

Notas de Aula 2 – Dinâmica dos Sólidos – Prof. Dr. Cláudio S. Sartori
F
8
   0.35  72.58
rad
12
 
   1.209 2
14
s
xi
N  FAB  cos  0
N  FAB  cos
2  02  2    
F
 2  02
2 
0  2  f0
yi
 
 
02   2 f0 
 0  N  FAB  cos  0
i
0
i
2
2 
4 2 f 02
  
2 
2
 360 
4 

60 

  
2   1.209 
  587.76rad

587.76
n
n
2
2
2
n  93.5
9. (Beer & Johnston 16.30 10ª Ed.) O disco
de 180 mm de raio está em repouso, quando ele é
colocado em contacto com uma correia em movimento a
uma velocidade constante. Negligenciando o peso da
ligação AB e sabendo que o coeficiente de atrito cinético
entre o disco e a correia é de 0.40, determinar a aceleração
angular do disco, enquanto ocorre escorregamento.

FAB  sen  P  FAt  0
P  FAt  FAB  sen
P  FAt FAB  sen

N
FAB  cos 
P  FAt
 tg
N
TMA:
M
O
 IO  
i
Fat  r  IO 
  N  r  IO 
IO 
 r
 I  
P     O 
   r   tg
I 
 O
 r
N 
IO  
 I  
 tg    O 
 r
  r 
m  g    r    IO   tg  IO 
P
N
FAt
 tg  IO    IO     m  g    r
m g   r
tg  IO    IO
m g  r

 tg     IO
m g  r
 
m  r2
 tg    
2
2  g
 
tg   r
2  0.4
10
 

0
tg 60  0.4 0.18
 
P

36
TCM:
 
0.8 10

2.132 0.18
Notas de Aula 2 – Dinâmica dos Sólidos – Prof. Dr. Cláudio S. Sartori
  20.84
rad
s2
10. (Beer & Johnston 16.38 10ª Ed.) Os
Discos A e B são aparafusados em conjunto, e os cilindros
D e E são ligados como mostrados para separar os cabos
envolvido nos discos. Um único cabo passa sobre discos
B e C. O disco A pesa 20 lb e os discos B e C pesam 12 lb
cada. Sabendo que o sistema é liberado a partir do
repouso e que nenhum deslizamento ocorre entre os cabos
e os discos, determinar a aceleração (a) do cilindro D, (b),
do cilindro E.
TB
TD
TE
 Cinemática do movimento:
r2 = r3 = 6 in; r1 = 8 in.
No equilíbrio: da polia AB: WD  8  WE  6  0
6
6
WD  WE  WD  18  WD  13.5lb
8
8
Como 15 > 13.5 o sentido de rotação da polia AB é
↺

Cálculo das massas:
mD 
WD
15lb
lb  s2


m

0.46584
D
g 32.2 ft s2
ft
mE 
WE
18lb
lb  s 2


m

0.55901
E
g 32.2 ft s2
ft

aD  aTA  aD  AB  r1
8
aD   AB 
12
aD  0.667   AB
aE  aTC
Cálculo dos momentos de Inércia:
1
1 20  8 
I A  mA  rA2  I A 
 
2
2 32.2  12 
2
r
6
 AB  3 C   AB  C   AB  C
r2
6
I A  0.138026 lb  s  ft 
TCM:

Bloco D:
mD  aD  WD  TA
0.4658  aD  15  TA
2
0.4658  0.667   AB  15  TA
IB  0.046584lb  s2  ft
I AB
R  m  aG   Fext

i
2
1
1 12  6 
I B  mB  rB2  I B 
 
2
2 32.2  12 
aTB  aTC  AB  r2  C  r3
IC  I B  0.046584lb  s2  ft
 I A  I B  0.138026  0.046584
0.3106

Bloco E:
mE  aE  TE  WE
0.559  aE  TE  18
6
0.559   AB   TE  18
12
I AB  0.18461lb  s2  ft 

TMA:
M
O
 IO  
i

Polia AB:
8
6
 TA   TB  I AB   AB
12
12
37
Notas de Aula 2 – Dinâmica dos Sólidos – Prof. Dr. Cláudio S. Sartori
8
6
 TA   TB  0.18641  AB
12
12

Polia C:
6
6
 TB   TE  IC  C
12
12
6
6
 TB   TE  0.04658  C
12
12
6
6
 TB   TE  0.04658   AB   AB  C
12
12

6
12
ft
aE  0.862 2
s
aE  1.7247 
11. O disco circular de massa m e raio r é rolar
através da parte inferior do percurso circular de raio R do
disco tem uma velocidade angular, a determinação da
força exercida pela N caminho no disco.
Equações:
0.3106   AB  15  TA


 0.559   AB  6  TE  18
12


6
8
 12  TA  12  TB  0.18641   AB

 6  T  6  T  0.04658  
B
E
AB

12
12

 0.3106   AB  15  TA
 0.2795    T  18

AB
E

8  TA  6  TB  2.23692   AB

 TB  TE  0.09316   AB
TCM:

Rn  N  Pn  m 
N  m g  m
i
Resolvendo o sistema:
rad
s2
TA  14.46lb
 AB  1.7247
TB  18.64lb
TE  18.48lb
aD  0.667   AB
aD  0.667 1.7247
ft
aD  1.15 2
s
aE  aTC  aE  C  r2  aE  AB  r2
R  m  aG   Fext
i
R  m  aG   Fext
0.3106   AB  TA  15


0.2795   AB  TE  18


2.23692   AB  8  TA  6  TB  0

 0.09316   AB  TB  TE  0
TCM:
v2
 v r
Rr


r2
N  m g 
2 
Rr


12. Um disco uniforme, com eixo fixo,
possui raio R = 0.4 m e massa m = 6 kg. Em repouso,
o disco é acionado pela força F = 20 N, através de
uma corda enrolada no mesmo. O atrito nos mancais
, gera um binário (momento) resistente Mres= 1.5
N.m. Pedem-se:
(a) a reação do eixo fixo.
(b) o número de voltas necessárias para
que o disco atinja a velocidade angular  = 40 rad/s.
M
F

TCM:
R  m  aG   Fext
i
38
v2
Rr
Notas de Aula 2 – Dinâmica dos Sólidos – Prof. Dr. Cláudio S. Sartori
H  m  ax  0
V  P  m  ay  0  V  P  m  g

TMA:
M
V  60N

TMA:
M
G
 IG  
R  F  M  IG  
m  R2

2
6  0.42
0.4  20  1.5 

2
RF  M 
6.5
0.48
rad
  13.54 2
s

 2  02  2       
 2  02  2       
 2  02
2 
40  0
2 13.54
  59.07rad
 
n
2
 2  02
2 
0 2  80 2
2   5.1
  627.45rad

627.45
n
2
2
n  100 voltas

59.07
n
2
2
  0    t  t 
t
13. A figura ilustra um volante, com massa m =
5.00 kg, raio R = 0.20 m, raio de giração k = 0.14 m,
girando com velocidade angular inicial 0 = 80 rad/s. No
instante t= 0s, aciona-se o freio do mesmo, que consiste
em comprimir a sapata do freio contra o volante, através
da fora F = 10 N. O coeficiente de atrito entre as
superfícies é µ = 0.25. Pedem-se.
(a) o instante em que o volante para;
(b) o número de voltas até parar.
F
R
TCM:
R  m  aG   Fext
i
H  F  m  ax  0  H  F
V  P  Fat  m  ay  0  V  P  Fat
39
 
n
n  9.4 voltas

 IG  
R  Fat  m  k 2 
R  Fat
 
m k2
R  N
 
m k2
0.2  0.25 10
 
5  0  0.142
rad
  5.1 2
s
i
2
G
i
80
 5.1
  0

t  15.68s
14. (Hibbeler -19.11 pg. 512) – Um motor
transmite um torque M = 0.05 N.m no centro da
engrenagem A do sistema de engrenagens acoplados,
onda as outras engrenagens são idênticas à engrenagem B
indicada. Determine a velocidade angular das
engrenagens A e B após t = 2s e a força F trocada entre as
engrenagens.
Notas de Aula 2 – Dinâmica dos Sólidos – Prof. Dr. Cláudio S. Sartori
F  0.2137N

TMA:
M
G
 IG  
i
Engrenagens A e B:
3  F  rA  M  I A    A 
F  rB  I B   B  F 
I B  B
rB
15. Um disco uniforme de massa m está
girando com velocidade angular 0 quando é colocado no
chão. Determine o tempo em que ele começa a rolar sem
escorregar. Qual é a velocidade angular do disco nesse
instante. O coeficiente de atrito cinético entre o disco e o
plano é µk. Qual o tempo que leva para adquirir essa
velocidade?
I 
3  B B  rA  M   I A   A
rB
B  rB   A  rA
r
40
 B   A  A   B   A    B  2  A
rB
20
I  2  A
3 B
 rA  M   I A   A
rB
3 2 
3 2 
mB  kB2
 A  rA  M  mA  kA2   A
rB
0.3  0.0152
  A  0.04  M  0.8  0.0312   A
0.02
0.00081 A  0.05  0.0007688   A
0.05
A 
0.00081  0.0007688
0.05
A 
0.0015788
 A  31.669
rad
s2
B  2  A  B  2  31.669
 A  31.669
rad
 B  63.339 2 ⭯
s
B  0  B  t  63.339  2
rad
⭯
s
A  0   A  t  31.669  2
B  126.67
A  63.338
rad
s
I 
F B B
rB
F
F
40
mB  k   B
rB
2
B
0.3  0.0152  63.339
0.02
Dados: g = 32.2 ft/s2;

ID 
1
m  R2
2
TCM:
R  m  aG   Fext
i
Fat  m  aT  Fat  m  ax  ax  k  g
N  P  0  N  m g

TMA:
M
G
 IG  
i
Fat  R  I g     

k  m  g  R
Ig
k  m  g  R
m  R2
2
2k  g

R
Quando o disco rola sem escorregar:
vG    R  vG  vG0  ax  t
vG0  0  vG    R  0  k  g  t  0
t
R
k  g
No movimento de rotação da roda:
  0    t
 g
  0  2 k  t
R
Notas de Aula 2 – Dinâmica dos Sólidos – Prof. Dr. Cláudio S. Sartori
  0  2
k  g   R

R k  g

1
3
  0  2    0
1 0  R
t
3 k  g

  0    t
v  0.375  25.76  t  v  9.66  t
v  v0  aG  t  9.66  t  8  3.864  t
9.66  t  3.864  t  8 13.524  t  8
t
8
13.524
t  0.5915s
a  t2
s  s0  v0  t 
2
3.864  t 2
s  8t 
2
3.864  0.59152
s  8  0.5915 
2
s  4.056 ft
TCM:
R  m  aG   Fext
Fx  m  ax  k  N  m  aG
 N
 N
aG  k
 aG  k
P
m
g
Fy  m  ay  0  N  P  0  N  P  16lb
17. O carretel de massa m = 100 kg possui raio
de giração kG = 0.3 m. Se os coeficientes de atrito estático
e cinético são, respectivamente, µS = 0.20 e µc = 0.15
determine a aceleração angular α do carretel se P = 50 N.
aG  k  g  0.12  32.2
ft
aG  3.864 2
s
TMA:
M
G
 IG  
i
Fat  R  I g     

2 R

k  m  g  R
k  m  g  R
2
m  R2
5
5  k  g

41
v
 0    t
R
v  R   t
2
I E  m  R2
5
i

Para que a bola role sem deslizar:
v R
16. Uma bola de boliche de peso 16 lb está num
plano com velocidade angular inicial nula e velocidade de
seu centro de massa v = 8 ft/s. Se o coeficiente de atrito
cinético entre a bola e a superfície é µk = 0.12, determine
a distância que a bola percorre sem escorregar.
Negligencie os buracos existentes para colocar os dedos
na bola.
Dados: g = 32.2 ft/s2;
5  0.12  32.2 19.32

2  0.375
0.75
rad
  25.76 2 ⭯
s
Ig
TCM:
R  m  aG   Fext
i
Fx  m  ax  P  FAt  m  aG
Fy  m  ay  0  N  W  0  N  W  m  g  1000

TMA:
M
i
G
 IG  
 P  r  Fat  R  I g    
Notas de Aula 2 – Dinâmica dos Sólidos – Prof. Dr. Cláudio S. Sartori
P  31510
P  450N
 P  r  Fat  R  m  k g2  
Se não há deslizamento, a aceleração tangencial
no ponto de contato do solo é a aceleração do centro de
massa:
aG    R
P  FAt  m    R
FAt  m    R  P
FAt  100    0.4  50  FAt  40    50
O
  15
H
 P  r   40    50   R  m  k g2  
50  0.25   40    50   0.4  100  0.32  
12.5  16    20  9  
25    32.5
32.5
25
rad
  1.3 2
s
FAt  m    R  P

FAt  100 1.3  0.4  50
FAt  2N
Como:
FAmax  s  N  0.2 1000  200  2
Observe que se houvesse arrastamento, a força
de atrito seria contrária à indicada, ou seja, para a
esquerda, caso a força de atrito fosse maior que 200 N,
valor da força de atrito de destaque, que é
FA  200N .

rad
s
P
V
TCM:
R  m  aG   Fext
i
Fx  H  m  an  H  m   2  r 
H   45   152 17.5
H  177.1kN
Fy  m  aT  0  V  P  m  r
V  m  g  m   r
V  450  45 817.5
V  450  6300 V  450  6300
V  5.850kN

TMA:
M
A
 I A 
i
IG 
max
Assim, ocorrerá rotação sem deslizamento...
18. Uma turbina heólica leve consiste em um
rotor que é alimentado a partir de um torque aplicado em
seu centro. No instante dado, o rotor está na horizontal
que tem uma velocidade angular de 15 rad/s e uma
aceleração angular no sentido horário de 8 rad/s2.
Determine a força normal interna, a força de cisalhamento
e o momento em uma seção passando pelo ponto A.
Suponha que o rotor é uma haste esbelta de 50 m de
comprimento, com uma densidade de massa de 3 kg/m.
rad
s2
G
Substituindo em:
Fat
  8
r = 7.5 m
MA
45 152
12
843.75
m L
 I O  3375kg  m2
3
M A  m  g  7.5  m    7.5   7.5  3375  8
IO 
2
M A  45 10  7.5  45  8  7.5  7.5  27000
M A  3375  20250  27000
M A  3375  20250  27000
M A  50.625kN  m
19. O sistema dado e abandonado do repouso da
posição mostrada. Determine a aceleração angular e o
momento na junção A. Cada barra tem massa m e
comprimento L.
G: Centro de massa da haste de 15 m à direita da seção A.
O peso dessa seção é:
P   l  g
42
Notas de Aula 2 – Dinâmica dos Sólidos – Prof. Dr. Cláudio S. Sartori

TCM:
R  m  aG   Fext
IG 
i
Fx  H  m  aT  H  m    2  r 
Fy  m  aT  V  2 P  m     r 

TMA:
M
A
 I A 
i
IG 
m  L2
12
(a) Anel:
Vamos calcular na unha o
momento de inércia de uma anel de raio r em
relação ao seu centro de massa G:
2
m
IG   r 2dm   r 2
rd  I G  m  r 2
2

r
corpo
0
IG  m  r 2
Aplicando o Teorema de Steiner e somando os
momentos de inércia das duas barras:
IA 
IA 
IO  IG  m  r 2  IO  2m  r 2
2
2

m  L2
m  L2
L
L 
 m  
 m   L2    

12
12
2
 2  

m L m L m L 5 L m



12
4
12
4
2  m  L2 6  m  L2
IA 

12
4
2
20  m  L
IA 
12
5  m  L2
IA 
3
2
2
M
2
A


 IO  
R  m  aG   Fext
i
m g
2
2
Fn  N  P  m  an  N  mg  m  0  r  N  m  g
Ft  T  m  aT  T  m    r  T  
(b) Disco:
L
5m L
 m g L 

2
3
3L 5  m  L2
m  g 

2
3
9 g
10 L
20. Determinar a aceleração angular e a
força sobre o rolamento em O para:
(a) o anel estreito de massa m;
(b) o disco circular plano de massa m;
imediatamente após que cada um é
libertado a partir do repouso no plano vertical
com OC horizontal.
43
O
TCM:
IG 
2
 
M
m  g  r  2m  r 2  
g
 
2r
i
m  g
TMA:
i
2
 I A 
m  r2
2
m  r2
2
3
IO  IG  m  r 2  IO  m  r 2
2

TMA:
M
O
 IO  
i
3
m  g  r  m  r 2  
2
2g
 
3r
21. Uma chapa uniforme de massa m com
o formato de um quarto de circulo é liberada a partir
do repouso com uma borda em linha reta vertical,
como mostrado. Determinar a aceleração angular
inicial e as componentes horizontal e vertical da
reação no pivô ideal em O.
Notas de Aula 2 – Dinâmica dos Sólidos – Prof. Dr. Cláudio S. Sartori
4b
m  b2
m  g  sen 
2

3
2
8 g 2
 

 2
3 b 2
8 g
 
3 b
Da figura, se você não faltou às aulas de GA:
Ox  N  sen  T  cos


IO 
corpo
2 b
Oy  N  cos  T  sen
m
rdrd
 b2
4
r 2 dm    r 2
0 0

 8 g  4b
T  m
2  m  g  sen450

 3 b  3
r b
2

4m
4m  r 4 

IO  2  r 3dr  d  I O  2       02
b 0
 b  4  r 0
0
b
IO 

4m b 
mb
  IO 
2
b 4 2
2
4
2
TCM:
R  m  aG   Fext
i
Ft  T  PT  m  aT  T  m  g  sen  m    r
T  m    r  m  g  sen
Fn  m  an  N  m  g  cos  m  2  r
  0  N  m  g  cos
2
2
4b
 4b   4b 
r  xG2  yG2        r 
2
3
 3   3 
cos  cos 450 

2
 sen  sen450
2
TMA:
M
O
 IO  
i
IO 
m  b2
2
Pt  r  IO  
m  b2
m  g  sen  r 

2
44
 1 32 
T  m  g 2   2 
 2 9 


 1 32 
Ox  m  g  cos  sen   m  g  2   2   cos 
2
9





2 2
 1 32  2
Ox  m  g 

 m g  2  2 
2 2
 2 9  2
1
 1 32 
Ox  m  g   m  g    2   1
2
 2 9 
1
1
32
Ox  m  g   m  g   m  g  2
2
2
9
32
Ox  m  g 2 
9
Oy  N  cos  T  sen

 1 32  
Oy  m  g  cos  cos   m  g 2   2    sen
 2 9  

2 2
 1 32  2
Oy  m  g 

 m g 2  2 
2 2
 2 9  2
1
 1 32 
Oy  m  g   m  g   2   1
2
 2 9 
1
1
32
Oy  m  g   m  g   m  g 2
2
2
9
32 

Oy  m  g   1  2  
 9 
22. A placa de aço uniforme de 20 kg é
livremente articulada em torno do eixo z, como mostrado.
Calcule a força suportada por cada um dos rolamentos em
A e B após o instante em que após a placa é libertada a
partir do repouso no plano yz horizontal. (Meriam Kraige
Cap.6 pag. 434). g = 9.81m/s2
Notas de Aula 2 – Dinâmica dos Sólidos – Prof. Dr. Cláudio S. Sartori

TMA:
M
O
 IO  
i
b m  b2
m  g  

2
3
3
g  
2b
36.78
Cálculo do momento de Inércia:
I

 
r 2dm
corpo
de uma chapa de comprimento b e altura h,
densidade uniforme m/(bh) em relação ao :
3g rad
2b s 2
147.15
196.2
0.4
20   36.78 
 20  9.81
2
RA 
2
RA  24.525N  RB
(i) Eixo x:
b
2

Ix 
h
2
m
m  h2
h y b  h dydx  12
2
b
 
2 2
(ii) Eixo y:
b
2
h
2

Iy 
b h
 
2 2
x2
m
m  b2
dydx 
bh
12
(ii) Eixo z:
Iz 
b
2
h
2
  x
2
b h
 
2 2
 y2 
m   b2  h2 
m
dydx 
bh
12
No exemplo, h = 250 mm e b = 400 mm
Usando o teorema dos eixos paralelos:
m  b2
m  b2
b
Iz 
 m  
12
3
2
2

TCM:
R  m  aG   Fext
i
Fx  2RA  P  m  ax  m   
RA 
m  
b
2
b
 mg
2
2
b
Fy  2RAy  m  ay  m  02   0
2
45
23. Uma roda de impulso para demonstrações
de dinâmica é mostrada na figura. É basicamente uma
roda de bicicleta modificada com aro, alças, e uma polia
para o arranque do cordão. O contra peso faz com que o
aro raio de giração da roda de 7 lb de peso mude de para
11 in. Se uma força estacionária de 10 lb é aplicada ao
cordão, determinar a aceleração angular da roda.
Despreze o atrito do rolamento.
Notas de Aula 2 – Dinâmica dos Sólidos – Prof. Dr. Cláudio S. Sartori
Podemos escrever:

dW  Ftan ds  ds  R  d
dW  Ftan R  d
dW    d
TCM:
R  m  aG   Fext
i
Fx  H  T  cos300  0
2
W     d
Fy  N  P  T  sen300  0
IG  m  k 2
1
P
7  11 
IG   k 2 
 
g
32.2  12 
2
P 2
7  11 
k 
 
g
32.2  12 
2
IG 
Podemos desenvolver:
dW    d
dW  I    d  dW  I 
d
 d
dt
dW  I   d
dW  I 
IG  0.18266 lb  ft 2

TMA:
M
O
2
 IO  
W   I    d
i
T 
2
 IO  
12
1
1
1
Wtot  I  22  I  12
2
2
dW
d
 
dt
dt
P   
2
 0.18266  
12
rad
  9.12 2
s
10 
24. Cada um dos dois discos de polimento
tem um diâmetro de 6 in, uma espessura de ¾ in, e
um peso específico de 425 lb/ft³. Quando ligada, a
máquina acelera do repouso até sua frequência de
funcionamento de 3450 rot/min em 5 s. Quando
desligado, ele chega ao repouso em 35 seg.
Determinar o torque do motor e momento de
fricção, assumindo que cada um é constante.
Despreze os efeitos da inércia da armadura
do motor rotativo....g = 32.2 ft/s2
d
 d
dt
 Energia do movimento de rotação
1
I  2
2
1
1
I   2  I  02
E
2
P 2
Como: P 
t
t
2     t  I  2  I  02
E
I   2  I  02
2    t
  0


 
2
2
I 

t
D
6
3
1
r   r   r  3in 
ft  ft
2
2
12
4
m g
 V
  e  r2

m
m
V
g
g

 Trabalho e potência no movimento de
rotação
2
m
425  3 1   1 
         m  0.1619667
32.2  4 12   4 
I Dis cos  2
46
m  R2
0.1619667
 I Dis cos 
2
16
Notas de Aula 2 – Dinâmica dos Sólidos – Prof. Dr. Cláudio S. Sartori
Fx  Fat  m  aG  m  g  sen
I Dis cos  0.01012lb  ft 2
f  3450
rot 3450

 f  57.5Hz
min
60
  2 f    2  57.5    361.2831

Fy  N  P  cos  0  N  m g  cos
N  W  cos   N  8  cos 400
N  6.12lb
rad
s
IG 
Ligando:
  0    t  361.281  0    5
rad
s2
I 
f 
t
0.0101229  361.281

5
 f  0.731lb. ft

Desligando:
  0    t  0  361.281    35
rad
s2
I 
f 
t
0.0101229  361.281

35
 f  0.0104lb. ft
  10.322
25. O cilindro sólido homogêneo é liberado a
partir do repouso sobre a rampa. Se  = 40° , s = 0.30 e
k = 0.20, determinar a aceleração do centro de massa G
e a força de atrito exercida pela rampa do cilindro.
Dados:
1 in 
1
ft
ft ; g  32.2 2
12
s
TMA:
M
O
 IO  
i
  72.2566

m  R2 W  R2

2
2g
W  R2
Fat  R 

2g
2  g  Fat
 
W R
Para não ocorrer escorregamento:
aG    R
W
 aG  W  sen
g
W  2  g  Fat 
Fat    
  R  W  sen
g  W R 
Fat  2Fat  W  sen
Fat 
3 Fat  W  sen400
sen400
3
sen400
Fat  8 
3
Fat  1.714lb
Fat  W 
 
2  g  Fat
2  32.2 1.714
 
W R
6
8 
 12 
  27.59
rad
s2
aG    R  aG  27.59
aG  13.8
6
12
ft
s2
26. O carretel tem uma massa de 500 kg e um
raio de giro kG  1.3m . Ele repousa sobre a superfície

TCM:
R  m  aG   Fext
i
Fx  P  sen  Fat  m  aG
47
de uma correia transportadora para a qual o coeficiente de
atrito estático eo coeficiente de fricção cinética é s.= 0.5.
O coeficiente de atrito cinético é s.= 0.4. Se o
transportador acelera com ac = 1m/s2, determinar a tensão
inicial no fio e a aceleração angular da bobina. O carretel
está originalmente em repouso.
Notas de Aula 2 – Dinâmica dos Sólidos – Prof. Dr. Cláudio S. Sartori
1456.25
0.8
Fs  1.82031kN
T  2.32kN
Fsmax  s  N  0.5 4905
Fs 

TCM:
Fsmax  2.452kN  Fs
R  m  aG   Fext
Logo, não haverá escorregamento.
i
n
Rx    Fxi  m  aG  T  Fs

i 1
Ry     Fyi  0  N  m  g
n
i 1
N  m  g  500  9.81
4905 N


TMA:
 M O  IO  
i
IO  m kO2
T  0.8  Fs 1.6  m  kG2    
27. (atividade 4a) - Uma bola de boliche,
considerada uma esfera uniforme de massa m =
2.0 kg e raio R = 0.15 m é lançada sobre uma
pista, uma superfície horizontal áspera com uma
velocidade linear de translação v0 = 12 m/s e sem
velocidade angular. O coeficiente de atrito entre
as superfícies é  = 0.25. Ao tocar o solo, forças
presentes interrompendo o movimento de
translação e impondo movimento plano, que após
algum tempo, torna-se movimento de rolamento
sem escorregamento. Considerando o instante
em que o movimento passa a ser de rolamento
sem escorregamento, pede-se a velocidade do
centro de massa G ou CM da bola.
T  0.8  Fs 1.6   500 1.32  
845

aP  aG    GP      GP



aP  j  aG  i    k  0.8  j  0
aG  0.8   0
aG  0.8  
Para não haver escorregamento:
aC  0.8    1   
1
0.8
rad
s2
aG  0.8   aG  0.8 1.25
m
aG  1 2
s
  1.25
T  0.8  Fs 1.6   845 1.25
1056.25
500 1  T  Fs


1056.25  1.6  Fs  0.8  T
1056.25  500  0.8  1.6  Fs  0.8  Fs
48
F
iExt
i

m  aGx    N  a    g
 m  aG  

 N  P  0  N  m g
M
O
 IG  
i
2
IG  m  r 2
5
M
 O  IG  
i
Notas de Aula 2 – Dinâmica dos Sólidos – Prof. Dr. Cláudio S. Sartori
2
F  r  m  r 2 
5
2
  m  g  r  m  r 2  
5
2
5 g
  g  r      
5
2 r
vG  t  t1   8.6

vC  0
t  0  v  v0
v  t   v0  a  t
vG  t   v0    g  t
vC  vG    GC
0  vG  iˆ    kˆ  r  ˆj
Velocidade angular:
5 g
t
2 r
5   g 2v0
  t  t1   

2 r 7  g
5v
  t  t1    0
7 r
 t   
A esfera começará a rolar sem deslizar
quando o ponto de contato dela com o solo
possuir velocidade nula.
m
s
28. Um cilindro de revolução
homogêneo de massa m = 4.0 kg, raio R =
0.5 m, é abandonada do repouso, apoiada em
plano inclinado de um ângulo  = 30° com a
horizontal, rola sem escorregar ao longo do
mesmo. Pedem-se:
0  vG  iˆ    r  kˆ  ˆj
 iˆ
0  iˆ  vG  iˆ    r  iˆ  vG    r
v0    g  t    r
  t   0    t
5 g
  t   0 
t
0
2 r
5 g
t
2 r
5 g
v0    g  t   
t  r
2 r
5
v0    g  t    g  t
2
2v0
7
  g  t  v0  t  t1 
2
7  g
 t   

inércia do cilindro: IG  1 m  R2 .
2
(b) O mínimo coeficiente de
atrito entre o cilindro e o plano inclinado.
Velocidade linear
vG  t   v0    g  t
2v0
vG  t  t1   v0    g 
7  g
7v  2v0
2
vG  t  t1   v0  v0  vG t  t1   0
7
7
5
vG  t  t1   v0
7
5
vG  t  t1   12
7
49
(a) A aceleração do centro de
massa G do cilindro. Dado: momento de

TCM:
R  m  aG   Fext
i
Fx  P  sen  Fat  m  aG
Fat  m  g  sen  m  aG
Fy  N  P  cos  0  N  m g  cos
m  R2
IG 
2

TMA:
M
i
O
 IO  
Notas de Aula 2 – Dinâmica dos Sólidos – Prof. Dr. Cláudio S. Sartori
m  R2
 Fat  R 

2
2 F
2  Fat
   at  aG    R 
m R
m
 Fat  m  g  sen  m  aG

2  Fat

aG 

m

m  g  sen
3
20
Fat 
N
3
Fat    N    m  g  cos
m  g  sen
  m  g  cos 
3
tg

3
0
tg 30
3


 0.193
3
9
Fat 
aG 
50
2  Fat 10
m
  3.33 2
m
3
s
Dinâmica dos Sólidos – Prof. Cláudio S. Sartori
Notas de aula 02 – 2° Bimestre
Ardeu?
Estuda aí, hein, carinha!?!?
51
 Dados:
g = 32.2 ft/s2 = 9.81 m/s2
1 ft = 0.3048 m
1 mi = 5280 ft = 5280.(0.3048 m) = 1609 m
1 in = 1/12 ft = 0.0254 m
1 ft = 0.3048 m
1 lb = 4.448 N
1 slug = 1 lb.s2/ft = 14.59 kg
g = 32.2 ft/s2 = 9.81 m/s2
1 ft = 0.3048 m
1 mi = 5280 ft = 5280.(0.3048 m) = 1609 m
1 in = 1/12 ft = 0.0254 m
1 ft = 0.3048 m
1 lb = 4.448 N
1 slug = 1 lb.s2/ft = 14.59 kg
Feliz
🎅
Quero ver você não chorar
Não olhar pra trás
Nem se arrepender do que faz
Quero ver o amor crescer
Mas se a dor nascer
Você resistir e sorrir
Se você pode ser assim
Tão enorme assim eu vou crer
Que o natal existe
Que ninguém é triste
Que no mundo há sempre amor
Bom natal
Um feliz natal
Muito amor e paz prá você
Prá você
Valeu ?
Estuda, carinha..
51