construção de maquete com software sketchup no

1
CONSTRUÇÃO DE MAQUETE COM SOFTWARE SKETCHUP NO ENSINO E
APRENDIZADO DE GEOMETRIA
1
2
3
Amanda Ferreira Procek , Aline Ferreira Rodrigues , Ana Cristina Polli , Thadeu Angelo
4
Miqueletto , Anderson Roges Teixeira Góes
1
5
PIBID/UFPR – Subprojeto Matemática 3
e-mail: [email protected]
2
PIBID/UFPR – Subprojeto Matemática 3
e-mail: [email protected]
3
PIBID/UFPR – Subprojeto Matemática 3
e-mail: [email protected]
4
Secretaria Estadual de Educação do Paraná
e-mail: [email protected]
5
Departamento de Expressão Gráfica - UFPR
e-mail: [email protected]
RESUMO
Esta atividade envolvendo a construção de uma maquete foi realizada no Colégio Estadual Padre
Cláudio Morelli com alunos do Ensino Médio, para isto foi utilizado o software Sketchup. O
desenvolvido ocorreuu sob supervisão dos participantes do Programa Institucional de Bolsa de
Iniciação à Docência (PIBID) - Subprojeto Matemática 3 - da Universidade Federal do Paraná
(UFPR). O objetivo foi desenvolver conceitos de geometria de forma prática, investigando uma melhor
forma de obter a altura de grandes paredes. Com isso, foram aplicados conceitos da trigonometria
utilizando um teodolito e trenas. Posteriormente, foram utilizados régua e compasso, materiais para a
confeccção de esboço dos prédios traçando assim retas paralelas e perpendiculares. Com o esboço
pronto, os estudantes realizaram a construção da maquete no software, criando assim a maquete
virtual. Nesta proposta, tivemos como fundamentação a Modelagem Matemática que consiste em
representar a realidade, explicando ou analisando algo motivando a resolução de um problema.
Ainda, dentro desta perspectiva, por termos realizado maquetes (manual e virtual), afirmamos que
esse trabalho está inserido no campo de estudos Expressão Gráfica. Assim, temos a aplicação de
conceitos matemáticos de forma lúdica e interessante para alunos do ensino médio, motivando-os
através de uma aplicação que envolve conceito com realidade. Então, concluimos que é necessário
trazer mais atividades utilizando a Modelagem Matemática, despertando nos alunos um maior
interesse de aprender os conceitos matemáticos.
Palavras-chave: Expressão Gráfica, Modelagem Matemática, Geometria e Software Sketchup.
2
1 INTRODUÇÃO
No Colégio Estadual Padre Claudio Morelli foi realizado pelos alunos da
Universidade Federal do Paraná (UFPR), participantes do Programa Institucional de
Bolsa de Iniciação à Docência (PIBID) - Subprojeto Matemática 3, uma atividade que
consiste em medir todos os prédios da escola para ser construída uma maquete
virtual por meio do software Sketchup.
Tal atividade foi trabalhada com alguns estudantes do Ensino Médio, que
anteriormente foram escolhidos pelo professor de matemática da escola e supervisor
do PIBID nesse projeto, pois estes eram os que mais se interessavam e se
dedicavam na disciplina da matemática. Com isso, planejamos para eles uma
atividade mais lúdica e interessante, mas que envolvesse a investigação de
diferentes formas de resolução de um problema, ou seja, comparar a matemática
com a realidade, e onde e como podemos usá-la para facilitar nosso trabalho.
Uma das tarefas a ser realizada na atividade consistia em medir paredes,
portas, janelas e prédios inteiros, devido a isto foram trabalhados conceitos de
geometria, trigonometria, desenho geométrico, sistemas de medidas e escalas.
Estes conceitos são algumas formas de resolver os problemas obtenção de grandes
alturas facilmente, e, além disso, promove a aprendizagem de forma mais rápida
nesses conceitos, visto que os alunos preferem aulas mais produtivas, ou seja,
aprendem fazendo.
Como a atividade teve como intuito construir uma maquete da escola
virtualmente, isto é, no computador, escolhemos o software Sketchup. Este software
é utilizado geralmente por profissionais engenheiros, arquitetos, designers,
construtores, e entre outros, para a criação de desenhos arquitetônicos, como
casas, edifícios, estruturas e entre outros, com facilidade e rapidez, pois as
ferramentas são simples para criação de formas em terceira dimensão. Com isso, os
alunos podem entender basicamente sobre como esses profissionais trabalham para
construir seus projetos, e de certa forma, contribuindo para as escolhas de
profissões dos alunos.
Desse modo, podemos perceber que a Expressão Gráfica está presente no
decorrer da atividade, visto que
A Expressão Gráfica é um campo de estudo que utiliza elementos de
desenho, imagens, modelos, materiais manipuláveis e recursos
computacionais aplicados às diversas áreas do conhecimento, com a
finalidade de apresentar, representar, exemplificar, aplicar, analisar,
formalizar e visualizar conceitos. Dessa forma, a expressão gráfica pode
auxiliar na solução de problemas, na transmissão de ideias, de concepções
e de pontos de vista relacionados a tais conceitos. (GÓES, 2013, p. 12).
Além de tudo, temos ainda a aplicação do conceito de Modelagem
Matemática, pois é o principal foco da atividade, que
pode ser descrita em termos de uma situação inicial, onde se tem um
problema, e de uma situação final desejada, no qual representa uma
solução para a situação inicial, e de um conjunto de procedimentos e
3
conceitos necessários para passar da situação inicial para a situação final.
(ALMEIDA, SILVA, VERTUAN, 2012, p. 12).
Ainda, outro objetivo da atividade foi ajudar os alunos a terem facilidade de
identificar, compreender e utilizar alguns conceitos da Matemática numa atividade
solução-problema. Além de poderem aprender mais como utilizar materiais
manipuláveis, como por exemplo, do desenho geométrico, sendo alguns deles
esquadros, régua, compasso, trena e um teodolito, que o próprio colégio obtinha que
possibilitou os alunos utilizarem e aprenderem conceitos de trigonometria através
dele, e também a utilização do software voltado para geometria, escala e
construção.
Por fim, durante esse artigo será inicialmente abordada à fundamentação
teórica, apresentando a base e as ideias principais da atividade, também
segundamente terá a apresentação da metodologia de pesquisa, no qual toda a
aplicação da atividade será explicada detalhadamente e finalmente as
considerações finais e referências.
2 DESENVOLVIMENTO
Uma das funções do PIBID é introduzir os alunos das licenciaturas na
escola, para que possam vivenciar sua futura profissão, e através disso podemos
experimentar algumas metodologias que poderão ajudar no planejamento de uma
atividade e também no processo de ensino/aprendizagem dos alunos quando
estivermos à frente de uma sala de aula. Essas metodologias são: o incentivo aos
alunos a investigarem, ou seja, utilizar da ferramenta de Investigação Matemática,
também utilizar materiais manipuláveis e recursos computacionais, isto é, aplicar a
Expressão Gráfica, e ainda utilizar a Modelagem Matemática que engloba todos
esses conceitos e ainda relaciona com a realidade.
Algo que faz com que os alunos se interessem mais pela matemática é a
sua exposição relacionando com a realidade, ou seja, mostrando que a matemática
esta presente no nosso dia-a-dia e que não é somente cálculos e conceitos, mas sim
que se têm diversas aplicações. Dessa maneira, podemos introduzir o conceito de
Modelagem Matemática que
pode ser descrita em termos de uma situação inicial (problemática), e de
uma situação final desejada (representa uma solução para a situação
inicial), e de um conjunto de procedimentos e conceitos necessários para
passar da situação inicial para a situação final. Nesse sentido, relações
entre realidade (origem da situação inicial) e Matemática (área em que os
conceitos e os procedimentos são abordados), servem de subsídio para que
conhecimentos matemáticos e não matemáticos sejam acionados,
produzidos ou integrados. Essa situação inicial problemática se chama de
situação-problema, e a situação final é associada à representação
matemática, ou seja, um modelo matemático. (ALMEIDA, SILVA,
VERTUAN, 2012, p. 12).
A Figura 1 que mostra sobre a situação final e inicial na Modelagem
4
Matemática.
Figura 1: Situação inicial e situação final na Modelagem Matemática
Fonte: ALMEIDA, SILVA, VERTUAN (2012), modificada pelos autores
O problema referido nessa definição quer dizer que ainda não se tem a
princípio um esquema para a sua solução, ou seja, para situações-problemas não se
tem procedimentos pré-definidos, ou conhecidos, segundo Almeida, Silva e Vertuan
(2012). Ainda, segundo autor, um modelo matemático é algo que representa a
realidade, que obtém medidas a fim de representar, explicar ou analisar algo, porém,
não somente visa à representação por si só, mas sim motivar a solução de um
problema através de tal reprodução.
Sobre modelagem, Houaiss (2009), define como dar forma a algo através
de um modelo. Assim, temos que a Modelagem Matemática tem como intuito motivar
soluções para problemas por meio de modelos matemáticos.
Com relação à atividade de Modelagem Matemática
ela envolve etapas relativas ao conjunto de procedimentos necessários para
configuração, estruturação e resolução de uma situação-problema que se
caracterizam como: inteiração, matematização, resolução, interpretação de
resultados e validação”. (ALMEIDA, SILVA, VERTUAN, 2012, p. 15)
Como mostra a figura abaixo sobre as etapas.
Figura 2: Fases da Modelagem Matemática
Fonte: ALMEIDA, SILVA, VERTUAN (2012), modificada pelos autores.
Na figura 2, Inteiração significa “inteirar-se” ou “informar-se” sobre algo, e no
caso da atividade de Modelagem Matemática temos que a inteiração é uma
representação de um primeiro contato com a situação-problema, conduzindo assim
para uma formulação dos problemas e definição de metas para sua resolução. Por
5
mais que seja a etapa inicial, ela pode se estender durante a atividade, pois podem
surgir necessidades de novas informações.
A Matematização indicada na Figura 2, segundo Freudenthal (1973, p.43,
citada por Almeida, Silva e Vertuan, 2012, p.16), se “caracteriza por dar o significado
matemático para a realidade”, ou seja, na fase da inteiração ainda não se tem
explicito a linguagem matemática, mas sim a linguagem natural, que é a realidade.
Com isso é necessário uma transformação da linguagem natural para a matemática,
através de buscas e elaboração de uma representação matemática de acordo com
conceitos, técnicas e procedimentos adequados para representar matematicamente
essas características.
Ainda descrevendo a Figura 2, a Resolução consiste em criar o modelo
matemático a fim de representar a situação, permitindo a analise de aspectos
relevantes e responder as perguntas formuladas sobre o problema. E, por fim, a
Interpretação dos resultados e Validação é o momento em que se realiza a análise
da resposta e valida a representação matemática relacionada ao problema. Essa
fase constitui de procedimentos necessários para a realização da atividade
Modelagem Matemática, ou seja, nesse momento se evidencia as características
desse tipo de atividade. (ALMEIDA, SILVA e VERTUAN, 2013, p.17), isto é,
No início se tem a situação-problema;
Os procedimentos de resolução não são pré-definidos e as soluções
não são conhecidas;
Ocorre a investigação de um problema;
Introdução e aplicação de conceitos matemáticos, e;
Ocorre a análise da solução.
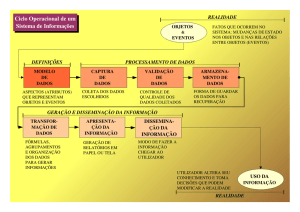
Na figura 3 temos os elementos que caracterizam a atividade de modelagem
matemática.
Figura 3: Os elementos que caracterizam uma atividade de Modelagem Matemática
Fonte: ALMEIDA, SILVA, VERTUAN (2012), modificada pelos autores.
Almeida, Silva e Vertuan (2012) considera que a atividade de Modelagem
Matemática pode ser incluída nas aulas regulares e é uma alternativa pedagógica
que pode ser utilizada não só para situações-problemas de Matemática. Esta
estratégia metodologica envolve um conjunto de ações cognitivas de um indivíduo,
trabalha a análise de objetos manipuláveis de matemática e é direcionada para
objetivos e metas estabelecidas ou reconhecidas pelo aluno. Com isso, desenvolve
a comunicação e argumentação capaz de convencer aos próprios modeladores
6
àqueles aos quais esses resultados são acessíveis de que a solução é verdadeira.
1.2 Metodologia e análise
Inicialmente foi proposta aos alunos a atividade, que consistia em criar uma
maquete da escola virtualmente no software Sketchup, com isso utilizamos um
conceito de Modelagem Matemática. (FIGURA 04)
Figura 4: Situação inicial e situação final da Modelagem Matemática, ou seja, construção da maquete
Fonte: os autores
Medir a escola foi a situação-problema. Um dos procedimentos foi utilizar
trenas para medir toda a escola, ou seja, todas as paredes, prédios, janelas, portas,
alturas, larguras, comprimentos e entre outros. Para registo, os alunos desenharam
cada objeto e anotaram todas as medidas, para se localizarem posteriormente. Para
isto, os alunos foram divididos em trios, onde cada trio ficou responsável por medir
um prédio ou setor, no qual eles puderam trabalhar em equipe fazendo com que as
atividades estivessem divididas para cada aluno. (FIGURA 5)
Figura 5: Etapa em que os alunos estavam medindo o setores da escola
Fonte: Os autores
Aplicando a inteiração, foi proposta uma pesquisa no final de três aulas: na
primeira aula a pesquisa estava realionada a as formas de medir a altura de um
prédio; a segunda pesquisa foi sobre tipos de escalas; e a terceira pesquisa sobre
algum software de design gráfico e construções.
Estas pesquisas auxiliaram nos próximos passos, aparecendo nesse
momento a oportunidade de investigar, pois os alunos estavam se perguntando
como medir a altura dos prédios e que seria difícil medir somente com a trena.
Então, então a pesquisa sobre as formas de medir a altura de um prédio ajudou
7
tanto os alunos a medir como conferir se algumas das alturas que obtiveram com a
trena estavam corretas. Um procedimento encontrado pelos alunos foi utilizando o
teodolito (FIGURA 6). Aliado a este equipamente, foram desenvolvidos conceitos de
trigonometria, que se identifica a matematização da Modelagem Matemática.
Figura 6: Etapa em que os alunos utilizaram o teodolito para medir as alturas
Fonte: os autores.
Após o término das conferências e correções das medidas, foi proposto aos
alunos à reprodução de todos os prédios em papel A3, conforme a separação em
equipes. Os estudantes utilizaram o que aprenderam da pesquisa sobre escalas
nesse passo, pois deveriam desenhar os prédios no papel proporcionalmente as
medidas que conquistaram na realidade. E ainda, tiveram que desenhar utilizando
régua, compasso e esquadros, pois não era para reproduzir um desenho simples,
mas sim aplicando conceitos do desenho geométrico, ou seja, fazendo construção
de perpendiculares e paralelas com compasso e esquadros. Para isso tiveram um
momento de instrução de como fazer e utilizar esses os objetos. (FIGURA 7)
Figura 7: Reprodução das informações em folha A3
Fonte: os autores.
Esses desenhos foram realizados com o intuito de serem aplicados os
conceitos do desenho geométrico, para os alunos terem um contato maior com
esses objetos e também para serem utilizados como base para o próximo passo que
era a construção no software Sketchup.
Nessa etapa da atividade podemos identificar além da matematização, o
8
conceito de Expressão Gráfica, quanto aos objetos geométricos e posteriormente a
utilização de recursos computacionais para a construção da maquete virtual. E
também de modelos matemáticos, pois os desenhos que reproduziram na folha já
representa algo que era real e que utilizou conceitos da matemática para poderem
fazer o desenho.
Por fim, na última etapa foram construídos os prédios da escola no software
Sketchup (FIGURA 8). Para isso, eles tiveram que analisar todos os desenhos que
realizaram na folha A3 e reproduzir para o programa que utilizava outra escala.
Figura 8: Etapa da reprodução do desenho da escola no software
Fonte: os autores
Temos que os alunos estavam construindo um dos prédios da escola,
conforme visto na Figura 8, lembrando que os mesmos estavam separados em
equipes inclusive nessa etapa, e a seguir na Figura 9, temos esse mesmo prédio
sendo desenhado diretamente visto do software Sketchup.
Figura 9: Os alunos executando o desenho
Fonte: os autores
Na Figura 10, temos um dos prédios da escola concluído.
9
Figura 10: Um dos prédios da escola finalizado no software Sketchup
Fonte: os autores
1.3 Análise
Podemos perceber nessa etapa a quarta fase da Modelagem Matemática,
que é a interpretação dos Resultados e Validação, ou seja, as informações que
obtiveram durante a atividade e aplicaram no modelo virtual. Esse passo foi o mais
divertido e interessante, pois além de os alunos construírem todos os prédios de sua
escola usando todas as medidas que obtiveram também aperfeiçoaram com figuras
e cores, para deixar mais parecido ainda com a realidade da escola. Essa etapa foi
realizada mais rapidamente e ajudou os alunos a entenderem basicamente como é o
trabalho de um arquiteto ou engenheiro, tornando assim a atividade mais
contagiante. No fim, das construções no software Sketchup, obtivemos resultados
incríveis, pois foram feitos com cuidado e dedicação, obtendo assim a maquete da
escola. Então, finalmente temos a situação final da atividade, que precisou de vários
procedimentos, adequações e analises para ser finalizado, mas que foi
excepcionalmente diferente e divertido para os alunos.
3 CONSIDERAÇÕES FINAIS
O objetivo dessa atividade foi motivar os alunos em relação à disciplina de
matemática, trazendo a eles aulas com mais aplicações a realidade, mais lúdicas e
que instigasse os alunos a quererem aprender matemática.
No decorrer dessa atividade de Modelagem Matemática, foi possível perceber
que os alunos ficaram mais entusiasmados, pois era uma atividade mais
interessante que trabalhava tanto a teoria da disciplina de matemática quanto a
prática, isto é, mostrava conceitos da matemática na realidade no meio em que os
alunos vivem. Ainda, era uma atividade em que eles deveriam investigar e descobrir
os conceitos e soluções sozinhos tendo os estudantes da UFPR como mediadores,
ou seja, eles identificavam um problema e direcionavam as pesquisas a serem
realizada.
10
Durante a atividade os alunos tiveram certas dificuldades relacionadas a
utilização de objetos geométricos e conceitos do desenho geométrico, pois
atualmente não é trabalhado isso nas escolas, apesar de ser uma atribuição do
professor de Matemática o desenvolvimento de tais conceitos. No entanto, ao
utilizarem os objetos eles se acostumaram e gostaram da facilidade de se executar
as perpendiculares e paralelas, portanto, os obstáculos encontrados foram
superados pela aprendizagem e pela ludicidade da atividade.
Em suma, esse tipo de atividade é muito válido e importante, pois incentiva os
alunos a investigarem mais, isto é, eles resolverem o próprio problema. Isso trabalha
muito no sentido da pesquisa, estudos e interesse em saber mais sobre algo que
eles gostam, e além de tudo, ter a oportunidade de poder ver a matemática ser
aplicada na realidade e num lugar onde eles frequentam, se torna mais lúdica e
contagiante de estudar, e faz com que promova a aprendizagem e soluções de
problemas, da matemática, mais facilmente.
E por fim, para o professor também é importante esse tipo de atividade, pois
faz com que os alunos trabalhem mais e aprendam sozinhos, e o professor fica
como um mediador, fazendo com que os alunos pensem nas soluções e resolvam
os problemas somente sendo instigados e motivados, trabalhando o
ensino/aprendizagem.
REFERÊNCIAS
ALMEIDA, L. W.; SILVA, K. P.; VERTUAN, R. E. Modelagem Matemática na
Educação Básica. São Paulo: Contexto, 2012.
GÓES, H. C. Um esboço de conceituação sobre Expressão Gráfica. Revista
Educação Gráfica, Bauru/SP v. 17, n. 1. 2013.
HOUAISS, A. Dicionário Houaiss de Lingua Portuguesa. Editora Objetiva. 2009.
FREUDENTHAL, H. Mathematics as an education task. Dordrecht: Kluwer, 1973.