As equações de Maxwell para meios não condu

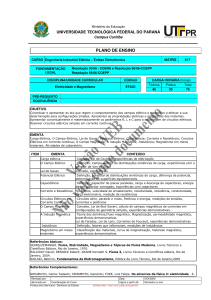
As equações de Maxwell para meios não condutores, lineares, homogêneos e isotrópicos
Mesmo no caso não estático, quando os campos e as fontes podem depender do
tempo, ainda assim as equações de Maxwell macroscópicas podem ser escritas
como
∇ · D = 4πρ,
∇ · B = 0,
∇×E =
−
1 ∂B
c ∂t
e
∇×H
=
4π
1 ∂D
J+
,
c
c ∂t
onde
D = E + 4πP
e
H
= B − 4πM.
Aqui, é claro, P é a polarização e M é a magnetização. Para um meio não
condutor, linear, homogêneo e isotrópico,
P
= χe E
e
M = χm H,
onde χe e χm são as susceptibilidades elétrica e magnética, respectivamente. O
meio é não condutor porque, mesmo havendo campo elétrico aplicado ao meio,
não há corrente livre. O meio é linear porque a polarização e a magnetização
dependem linearmente dos campos elétrico e intensidade magnética, respectivamente. O meio é homogêneo porque as susceptibilidades não dependem da
posição no meio. Como as direções da polarização e da magnetização induzidas
são paralelas, respectivamente, aos campos elétrico e intensidade magnética, o
meio é dito isotrópico; será dito anisotrópico quando a polarização for ao longo
de uma direção não paralela ao campo elétrico ou quando a magnetização for
ao longo de uma direção não paralela ao campo intensidade magnética.
1
Para um meio não condutor, linear, homogêneo e isotrópico,
D = E + 4πP
= E + 4πχe E
= (1 + 4πχe ) E
= εE,
onde definimos a permissividade elétrica do meio como
≡ 1 + 4πχe ,
ε
e
H
= B − 4πM
= B − 4πχm H,
ou seja,
B = H + 4πχm H
= (1 + 4πχm ) H
= µH,
onde definimos a permeabilidade magnética do meio como
µ ≡ 1 + 4πχm .
Substituindo
D = εE
e
H
=
B
µ
nas equações de Maxwell macroscópicas acima, obtemos
∇ · (εE)
= 4πρ,
∇ · B = 0,
∇×E =
e
(
∇×
B
µ
)
−
1 ∂B
c ∂t
4π
1 ∂ (εE)
J+
,
c
c ∂t
=
2
que, como estamos supondo ε e µ constantes na região do meio, também podem
ser escritas como
ρ
∇ · E = 4π ,
ε
∇ · B = 0,
∇×E =
−
1 ∂B
c ∂t
e
∇×B =
µε ∂E
4πµ
J+
.
c
c ∂t
3