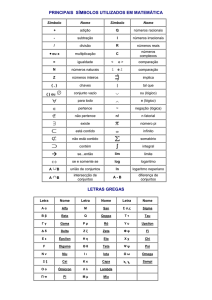
CONJUNTOS NUMÉRICOS 15 [Somente leitura] [Modo de

CONJUNTOS NUMÉRICOS
CONJUNTOS NUMÉRICOS
O conceito de número foi evoluindo ao
longo dos tempos, tendo-se criado novos
números para responder a problemas
entretanto surgidos.
CONJUNTOS NUMÉRICOS
NATURAIS
INTEIROS
RACIONAIS
REAIS
CONJUNTOS NUMÉRICOS
NÚMEROS NATURAIS
7
Estes números foram criados
6
pela necessidade prática de
contar as coisas da natureza,
por isso são chamados de
5
números naturais.
1
2
3
4
CONJUNTOS NUMÉRICOS
NÚMEROS NATURAIS
A representação matemática deste conjunto é:
IN = {1, 2, 3, 4, 5, ... }
NÚMEROS INTEIROS
• Os números naturais não permitiam a
resolução de todas as operações. A subtracção
de 3 - 4 era impossível.
• A ideia do número negativo, aparece na
Índia, associada a problemas comerciais que
envolviam dívidas.
• A ideia do número zero surgiu também nesta
altura, para representar o nada.
NÚMEROS INTEIROS
A representação matemática deste conjunto é:
Z = {..., -3, -2, -1, 0, 1, 2, 3, ...}
NÚMEROS RACIONAIS
Entretanto...surgiu outro tipo de problema:
“ Como dividir 3 vacas por 2 herdeiros? “
Para resolver este tipo de problemas foram
criados os números fracionários. Estes
números juntamente com os números inteiros
formam os racionais.
NÚMEROS REAIS
Os pitagóricos ao determinar a
medida do comprimento da
diagonal de um quadrado de lado
unitário, não conseguiram
encontrar um número racional para
essa medida, surgindo dessa forma
os números reais.
REPRESENTAÇÃO NA RETA NUMÉRICA
• Os números relativos – positivos, negativos ou o zero
– podem ser representados numa recta por meio de
pontos.
• Consideremos uma recta r e marquemos sobre ela um
ponto O, a que chamamos origem.
• Escolhemos uma unidade de medida e um sentido
positivo (por exemplo da esquerda para a direita).
Desta maneira obtemos um eixo ou reta numérica.
O
-
1
r
+
REPRESENTAÇÃO NA RETA
Se quisermos marcar o ponto A correspondente ao número
+5, contamos 5 unidades para a direita de O.
-
O
+1
+5
+
A
Se quisermos marcar o ponto B correspondente ao número
-3, contamos 3 unidades para a esquerda de O.
-
-3
B
O
+1
+
REPRESENTAÇÃO NA RETA
O número que corresponde a um ponto do eixo chamamos
abcissa desse ponto.
-
-3
O
+1
+5
A
B
A abcissa de B é -3
A abcissa de A é +5
A origem tem abcissa zero.
+
ORDENAÇÃO
•Quando dispostos sobre um eixo, os números relativos
encontram-se ordenados.
•Se o eixo é horizontal e orientado da esquerda para a
direita, um número é tanto maior quanto mais para a
direita se encontrar.
-3
-2
-1
0
1
2
Cada vez maior
3
4
5
ORDENAÇÃO
Vemos, por exemplo, que +5 é maior que +2 e para indicar
este facto escrevemos:
+5 >+2
Também se pode dizer que + 2 é menor que + 5 e escrever:
+2 <+5
Isto é, se
-3
-2
então
a> b
-1
0
1
b<a
2
•
3
4
5
•
ORDENAÇÃO
Da observação da posição relativa de dois números num
eixo resultam algumas regras para comparar dois números
diferentes:
•Qualquer número positivo é maior do que zero.
+ 0,012 > 0
•Zero é maior que qualquer número negativo.
0 > - 35
•Qualquer número positivo é maior do que qualquer
negativo.
+1 > - 35
+ 0,5 > ;- 100
VALOR ABSOLUTO (OU MÓDULO)
Consideremos agora os pontos A e B, sendo que A tem
abcissa + 3 e B tem abcissa – 2.
-3
-2
-1
0
1
2
B
3
4
5
A
2
3
A distância do ponto A à origem é 3.
A distância do ponto B à origem é 2.
A essa distância chamamos valor absoluto ou módulo.
VALOR ABSOLUTO (OU MÓDULO)
Assim dizemos que o valor absoluto (ou módulo) de +3 é
igual a 3 e escrevemos:
+3 = 3
Portanto, temos ainda que
-2 = 2
Valor absoluto (ou módulo) de um número é a distância à
origem do ponto que representa esse número.
Naturalmente, temos que o valor absoluto de zero é igual a
zero:
0 =0
NÚMEROS SIMÉTRICOS
Relativamente à origem da reta, é sempre possível encontrar
dois pontos que se encontram à mesma distância.
-4
-3
-2
-1
0
1
2
3
4
Por exemplo, os pontos de abcissas – 4 e 4 têm a mesma
distância à origem, ou seja,
- 4 =
4
Dizemos então que – 4 e 4 são números simétricos.
NÚMEROS SIMÉTRICOS
•Dois números dizem-se simétricos se tiverem sinais
contrários e o mesmo valor absoluto.
Exemplos de números simétricos:
- 0,3 e 0,3
porque
1 e -1
porque
- 0,3 = 0,3
1
= -1
Nota que o simétrico do número zero é o próprio número
zero:
0
=
0
NÚMEROS SIMÉTRICOS
•Observação
1. De dois números positivos o maior é o que tem maior
valor absoluto (está mais longe da origem).
Exemplos:
+ 0,5 > + 0,1
+ 100 > + 40
2. De dois números negativos o maior é o que tem menor
valor absoluto (está mais perto da origem).
Exemplos: - 3 > - 50
- 0,01 > - 10
Números Simétricos
Simplificação da escrita
Na reta também se escreve 1, 2, 3,..., em vez de +1,+2,+3,...
-4
-3
-2
-1
0
1
2
3
Também:
+ (+ 8) = + 8
+ (- 8) = - 8
Não é obrigatório escrever o sinal +
4
NÚMEROS SIMÉTRICOS
Na reta numérica o maior dos números encontra-se à
direita do menor.
-4
-3
-2
0
-1
-2 é maior que - 4
2 é maior que - 1
2 >- 1
1
2
3
- 2> - 4
ou
- 1 é menor que 2
- 1< 2
> maior
4
< menor
Conjuntos numéricos
Formas de representação de um
conjunto numérico.
Extenso: A={2,3,4,5,6}
Algébrica: A={x∈N/1<x<7}
Diagrama:
Conjuntos importantes
• Conjunto vazio: C = {} ou C = ∅
• Conjunto unitário: B = {78}
• Conjunto Universo (U)
– Formado por todos os elementos com os quais
estamos trabalhando numa determinada
situação, ou seja, é o conjunto de todos os
conjuntos considerados em um problema.
Conjuntos/relações
A = {0,1, 2, 3, 4}
B = {1, 2}
C = {} ou C = ∅
1∈ A
{1} ⊂ A
{3} ⊄ B
B⊂ A
A⊄ B
∅⊂B
1 pertence a A
{1} está contido em A
{3} não está contido em B
B está contido em A
A não está contido em B
O conjunto vazio está contido em B
Conjunto das partes
• É formado por todos os subconjuntos de um
conjunto dado.
– B={1, 2, 3}
– P(B)={Ø, {1}, {2}, {3}, {1,2}, {1,3}, {2,3},
{1,2,3}}
Conjunto das partes
• Relação entre o número de elementos do
conjunto e o número de elementos do conjunto
das partes:
– Ø possui 0 elementos e P(Ø)={Ø} possui 1 elemento
– {1} possui 1 elemento e P({1})={Ø, {1}} possui 2
elementos
– {1, 2} possui 2 elementos e P({1,2})={Ø, {1}, {2},
{1,2}} possui 4 elementos
Operações com conjuntos:
Intersecção
• Seja o conjunto A={0, 1 ,2, 3, 4} e o
conjunto B={0, 2, 5, 6}, temos:
• A ∩ B = {x/x∈A e x ∈ B} (Intersecção)
• A ∩ B = {0, 2}
A
0
1
3
4
2
B
5
6
Operações com conjuntos:
União
• Seja o conjunto A={0, 1 ,2, 3, 4} e o
conjunto B={0, 2, 5, 6}, temos:
• A ∪ B = {x/x∈A ou x ∈ B} (União)
• A ∪ B = {0, 1, 2, 3, 4, 5 ,6}
A
0
1
3
4
2
B
5
6
Operações com conjuntos:
Diferença
• Seja o conjunto A={0, 1 ,2, 3, 4} e o
conjunto B={0, 2, 5, 6}, temos:
• A - B = {x/x∈A e x∉B} (Diferença)
• A - B = {1, 3, 4}
A
0
1
3
4
2
B
5
6
Operações com conjuntos:
Complementar
• Caso especial: um conjunto está contido no outro:
• A={0, 1 ,2} e B={0, 1, 2, 5, 6}, temos:
• O complementar de B em relação a A:
A
0
B
1
2
A ∪ B = {0, 1, 2, 5 ,6} = B
A-B={ }
5
C BA = B − A = {5,6}
6
A ∩ B = {0, 1, 2} = A
B-A={5, 6}
Operações com conjuntos:
Produto cartesiano
• Seja o conjunto A={0, 1 ,2, 3, 4} e o
conjunto B={0, 2, 5, 6}, temos:
• A x B = {(x,y)/x∈A e y∈B} (Produto cartesiano)
• AxB={(0,0); (0,2); (0,5); (0,6);
(1,0); (1,2); (1,5); (1,6);
(2,0); (2,2); (2,5); (2,6);
(3,0); (3,2); (3,5); (3,6);
(4,0); (4,2); (4,5); (4,6)}
• Atenção: n(A) = 5 e n(B)=4 e n(AxB)=5 . 4 = 20
• Par ordenado: (2, 0)≠(0, 2)
Representação no plano
cartesiano
A={0, 1 ,2, 3, 4}
B={0, 2, 5, 6}
B
Atenção para:
•AxB: A no eixo horizontal e B
no eixo vertical
• (0,2) e (2,0) são pontos
distintos
A
• Os pontos não estão ligados
por linhas contínuas, isso
depende dos conjuntos e da
relação!
Exercícios/Problemas
Problemas/Exemplo
Numa pesquisa realizada com 52 alunos sobre a preferência
de disciplinas apontou os seguintes dados:
I. 32 alunos gostam de matemática;
II. 30 alunos gostam de português;
III. 10 alunos não gostam de nenhuma dessas disciplinas.
De acordo como o exposto acima, responda:
A) Quantos alunos gostam de matemática e português?
B) Quantos alunos gostam de apenas matemática?
C) Quantos alunos gostam de matemática ou português?
Problemas
A.
B.
C.
D.
E.
Uma pesquisa realizada com professores de matemática sobre suas
referências musicais descobriu que 458 gostam de Sertanejo, 112
gostam de Samba, 62 gostam de ambos e 36 não gostam de
nenhum dos dois gêneros musicais. Sendo assim, o número de
professores que participaram da entrevista foi:
668
544
508
632
N.d.a.
Problemas
a.
b.
c.
d.
e.
– (FCC-BA) Consultadas 500 pessoas sobre as emissoras de TV a
que habitualmente assistem, obteve-se o resultado seguinte: 280
pessoas assistem ao canal A, 250 assistem ao canal B e 70 assistem
a outros canais distintos de A e B. o número de pessoas que
assistem a A e não assistem a B é:
100
150
180
200
210
Problemas
(ENEM – 2003) Os acidentes de trânsito, no Brasil, em sua maior parte são causados por erro do motorista.
Em boa parte deles, o motivo é o fato de dirigir após o consumo de bebida alcoólica. A ingestão de uma
lata de cerveja provoca uma concentração de aproximadamente 0,3 g/L de álcool no sangue.
A tabela abaixo mostra os efeitos sobre o corpo humano provocados por bebidas alcoólicas em função de níveis de
concentração de álcool no sangue:
Concentração de álcool no sangue (g/L)
Efeitos
0,1 - 0,5
Sem influência aparente, ainda que com alterações clínicas.
0,3 - 1,2
Euforia suave, sociabilidade acentuada e queda da atenção.
0,9 - 2,5
Excitação, perda de julgamento crítico, queda da sensibilidade e das reações motoras.
1,8 - 3,0
Confusão mental e perda da coordenação motora.
2,7 - 4,0
Estupor, apatia, vômitos e desequilíbrio ao andar.
3,5 - 5,0
Coma e morte possível.
(Revista Pesquisa FAPESP no 57, setembro 2000)
Uma pessoa que tenha tomado três latas de cerveja provavelmente apresenta
a) queda de atenção, de sensibilidade e das reações motoras.
b) aparente normalidade, mas com alterações clínicas.
c) confusão mental e falta de coordenação motora.
d) disfunção digestiva e desequilíbrio ao andar.
e) estupor e risco de parada respiratória.
Problemas
Num universo de 800 alunos, é sabido que 300 delas gostam de
matemática. 400, de português e 130, de matemática e português.
Quantas não gostam nem de matemática nem de português?
A.800.
B.230.
C.670.
D.430.
E.N.d.a..
Problemas
Problemas
(ENEM) Um fabricante de cosméticos decide produzir três diferentes
catálogos de seus produtos, visando a públicos distintos. Como
alguns produtos estarão presentes em mais de um catálogo e ocupam
uma página inteira, ele resolve fazer uma contagem para diminuir os
gastos com originais de impressão. Os catálogos C1, C2 e C3 terão,
respectivamente, 50, 45 e 40 páginas. Comparando os projetos de
cada catálogo, ele verifica que C1 e C2 terão 10 páginas em comum;
C1 e C3 terão 6 páginas em comum; C2 e C3 terão 5 páginas em
comum, das quais 4 também estarão em C1. Efetuando os cálculos
correspondentes, o fabricante concluiu que, para a montagem dos
três catálogos, necessitará de um total de originais de impressão
igual a:
(A) 135. (B) 126. (C) 118. (D) 114. (E) 110.
Problemas
A.
B.
C.
D.
E.
(UEPA) – A Câmara dos Deputados reuniu-se extraordinariamente para
decidir sobre a instalação de duas CPIs ( Comissões Parlamentares de
Inquérito): a do FUTEBOL e a do CAIXA 2. Dos 320 deputados
presentes, 190 votaram a favor da instalação da CPI do FUTEBOL;
200 pela instalação da CPI do CAIXA 2; 80 votaram a favor da duas
CPIs e X Deputados foram contrários à instalação das duas CPIs. O
número X de Deputados que votaram contra a instalação das CPIs é:
10.
90.
70.
20.
N.d.a.
Intervalos numéricos
(reais)
Intervalos numéricos
(Reais)
-3
(-3, +∞) = ]-3, +∞) ={x ∈ ℜ / x > -3}
-3
[-3, +∞) = [-3, +∞) ={x ∈ ℜ / x ≥ -3}
Intervalos numéricos
(Reais)
-3
4
(-3, 4) = ]-3, 4)=]-3, 4[ ={x ∈ ℜ / -3 < x < 4}
-3
4
(-3, 4] = ]-3, 4] ={x ∈ ℜ / -3 < x ≤ 4}
Operações com intervalos
Exemplo.
(UFV) Sejam os conjuntos A = {x ∈IR 1/ < x < 5 } e B =
{x ∈IR / 2 ≤ x ≤ 6 }. Então A ∩ B é:
a) {2 ,3 4 }
b) {x ∈IR 2/ ≤ x ≤ 5 }
c) {x ∈IR 2/ < x < 5 }
d) {x ∈IR 2/ < x ≤ 5 }
e) {x ∈IR 2/ ≤ x < 5 }
Exemplo
(PUC – MG) Sendo IR o conjunto dos números reais e sendo os conjuntos
A = {x ∈IR /− 5 < x ≤ 4 } e B = {x ∈IR /− 3 < x < 7 }, o conjunto A −
B é:
a) {x ∈IR /− 5 < x ≤ −3 }
b) {x ∈IR /− 3 ≤ x ≤ 4 }
c) {x ∈IR /− 5 < x < −3 }
d) {x ∈IR / 4 < x ≤ 7 }
Exercícios
1. (Mack – SP) Sejam os conjuntos A = {x ∈ IR /0 ≤ x ≤ 3 }, B = {x ∈ IR / x ≤ 3 }
e C = {x ∈ IR /− 2 ≤ x ≤ 3 } O conjunto (B − A) ∩ C é igual a:
a) ∅
b) {x ∈ IR /x < 0 }
c) {x ∈ IR /x > −2}
d) {x ∈ IR/ − 2 ≤ x < 0 }
e) {x ∈IR /− 2 < x ≤ 3 }
2. (PUC – RS) M = ( − ∞ , 3 ), N = [ − 1 ,+ ∞ ) e P = [− 2 ,10 ) são intervalos.
Então P − (M ∩ N) é igual a:
a) [ − 1,2 )
b) [ − 2 , 3 )
c) [− 2 , 10 )
d) ( − ∞, −1]∪ ( 3 , + ∞ )
e) [ − 2 , −1)∪ [ 3 , 10 )
Exercícios
3. Sejam os conjuntos A = {x ∈ IR /-1 < x ≤ 3 }, B = {x ∈ IR / 0 < x ≤ 7 } e C =
{x ∈ IR / x ≤ 3 }, determine:
A∩C
A∩B∩C
AUB
A–B
B–C
(A U B) – C
Exercícios
4. Para os intervalos A = {x ∈ IR /-1 < x}, B = {x ∈ IR / -5 < x < 5 } e C = {x ∈
IR / x ≤ 3 }, determine:
a) A ∩ B ∩ C
b) A – B
c) B – C
d) C – A
EXERCÍCIOS DO LIVRO
1 AO 8 DA PÁGINA 28.