E-mail: Lista de Exercícios

Departamento de Ensino- DE
Coordenação Geral de Ensino – CGE
Curso: AGRICULTURA
Disciplina: Matemática Aplicada a Agricultura
Prof. Ediênio Farias
E-mail: [email protected]
Aluno(a):______________________________________________________________ Módulo I
Turno: ____
Lista de Exercícios – MAA 002
Das questões 01 a 11, as respostas devem pertencer ao
Conjunto dos Números Inteiros.
1 – Imagine que no jogo “Atingindo ao alvo” você
tenha conseguido os pontos abaixo. Escreva o total de
pontos obtidos em cada jogada.
(registre os cálculos)










1ª jogada: - 6 + 3 + ( - 5) + 1
2ª jogada: - 5 + 5+ ( - 2) + 3
3ª jogada: 7 + (- 1) + 7
4ª jogada: - 1+ 3+ (- 6) + 5
5ª jogada: - 3 + 6 + 6
6ª jogada: - 4 + 3 + 4 + (- 4)
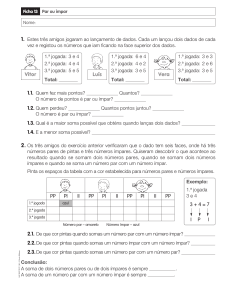
7ª jogada: - 6+ (- 7) + 2
8ª jogada: 1 + 10 + ( - 4)
9ª jogada: - 5 + 3 + ( - 7)
10ª jogada: - 2 + 8 + ( - 3) + 2
a) Qual a jogada de maior pontuação?
b) Qual a jogada de menor pontuação?
c) Qual a soma total dos pontos obtidos nas dez
rodadas?
2 – Seu Adalberto, pai de Célia, comentou que as
contas a pagar deste mês estavam muito altas. Mas
Seu Adalberto tem cheque especial, um tipo de conta
em que o banco permite que o cliente fique devendo
até R$ 200,00, em troca do pagamento de juros.
Acompanhe o extrato bancário e responda:
Saldo do mês anterior
Crédito do salário
Compras do mês
Contas (água, luz e celular)
Prestações em geral
Consulta médica
Gastos extras
R$ 183,00 D
R$ 748,00 C
R$ 180,00 D
R$ 92,00 D
R$ 217,00 D
R$ 171,00 D
R$ 64,00 D
a) Escreva uma expressão numérica onde
apareçam os valores do extrato com os sinais
adequados e resolva-a.
b) O que significa o resultado que você
encontrou? Seu Adalberto vai necessitar do
limite do cheque especial? Caso ele necessite,
quanto faltaria para alcançar o limite total
desse cheque especial?
3) Péricles teve gasto que não estavam previstos no
seu orçamento e acabou contraindo uma dívida de R$
270,00. Combinou pagá-la em três parcelas iguais,
sem acréscimo. Desse modo, Péricles dividiu sua
dívida em três partes iguais. Represente essa situação
com números inteiros e calcule o valor de cada parte
da dívida.
4) Lídia precisava de um empréstimo no valor de R$
940,00 e optou por fazer dívidas de R$ 235,00 em
diferentes bancos. Represente essa situação usando
números inteiros e descubra em quantos bancos ela
ficou devendo.
5) Na escola “Educa Sempre” estavam matriculados,
em janeiro, 1 378 alunos. Em fevereiro, foram
matriculados mais 4 alunos em cada uma das 5 classes
do 1º ano do Ensino fundamental e 23 alunos nas
demais séries. Em maio, 5 alunos de cada uma das
quatro classes de 4º ano pediram transferência para
outras escolas. No final do semestre, mais 12
estudantes pediram transferência. Como no ano
seguinte a escola seria reformada e permaneceria
fechada o ano inteiro, os alunos foram distribuídos,
igualmente, em 3 escolas da região. Quantos alunos
foram transferidos para cada uma dessas escolas?
Represente esse relato com uma expressão numérica e
calcule-a.
6) Indique e efetue as potenciações:
a)
b)
c)
d)
e)
f)
g)
h)
Base – 8 e expoente 3.
20 elevado ao cubo.
– 7 elevado ao quadrado.
Base 0 (zero) e expoente 5.
– 2 elevado à sétima potência.
Base – 1 e expoente 8
– 1 elevado à milésima potência.
+ 30 elevado ao cubo.
7) Registre cinco potenciações diferentes, todas com
resultado + 16.
8) Registre as raízes quadradas com resultados 0, + 1,
+ 2, + 3, até + 10.
Departamento de Ensino- DE
Coordenação Geral de Ensino – CGE
Curso: AGRICULTURA
Disciplina: Matemática Aplicada a Agricultura
Prof. Ediênio Farias
E-mail: [email protected]
9) Indique a expressão correspondente e calcule seu
valor:
a) A soma de – 6 com o dobro de + 5.
b) A metade da diferença entre – 4 e + 8.
c) O produto do quadrado de -3 com o cubo de –
2.
10) Invente e indique a operação:
a) Uma multiplicação com resultado – 20.
b) Uma divisão com dividendo negativo e
resultado + 3.
c) Uma potenciação com base negativa e
resultado + 1.
d) Uma raiz quadrada de número negativo com
resultado negativo.
e) Uma adição com resultado zero.
f) Uma subtração com os dois termos negativos
e resultado + 1.
g) Uma potenciação com base maior que + 10 e
resultado + 1.
11) Se x = - 4, y = - 6 e z = + 12, calcule:
a)
b)
c)
d)
e)
f)
g)
h)
x–y
(-4) . z
z:y
z–y
y+y
y.y
y–y
y:y
Das questões 12 a 41, as respostas devem pertencer ao
Conjunto dos Números Racionais.
14) O pêndulo de um relógio leva 3, 14 segundos para
fazer uma oscilação completa (ida e volta). Em quanto
tempo esse pêndulo fará 8 oscilações completas?
15) Um metro de certo fio tem 0,78 quilograma.
Quantos quilogramas terão 5,5 metros desse fio?
16) Em um terreno foram construídas 12 salas, todas
com 42, 25 metros quadrados de área. Se o terreno
tem 1 000 metros quadrados de área, de quantos
metros quadrados é a área livre desse terreno?
17) Determine o valor de cada uma das expressões
numéricas:
a)
b)
c)
d)
e)
f)
9,05 – 2,5 . 2,5
(6 – 1,07) . 3,1
7. 1,3 + 3,26 . 0,8
(11,1 – 7,99) . (10 – 9,98)
(2 . 1,1 + 3,83) : 0,9
1,2 . (4,8: 0,4 – 3 . 3,6)
18) Se um número x é expresso por 237 multiplicado
por 0,006. O um número y é expresso pelo dobro do
número 1,025 e o número z é expresso pelo quadrado
de 2,05, determine x + y + z.
19) Um pintor já pintou 85% da superfície de uma
parede. A parede toda tem 16,8metros quadrados de
superfície. Nessas condições, determine:
a) quantos metros quadrados da parede já foram
pintados?
b) Quantos metros quadrados ainda restam para
pintar?
20) Qual é o número decimal que representa 8% de
40%?
12) Ana Maria tem 1,63 metro de altura; Paula tem
1,7 metro; Cecília 1,54 metro e Renata 1,68 metro.
a) Escreva os nomes dessas pessoas na ordem
decrescente de altura.
b) Calcule a média aritmética dessas alturas.
21) Sabe-se que 124,5 litros de vinho devem ser
colocados, igualmente, em 15 tonéis. Quantos litros de
vinho serão colocados em cada tonel?
13) Uma caminhão pode transportar, no máximo, 3
000 quilogramas. Se ele deve levar 683, 5
quilogramas de batata, 1 562, 25 de cebola, 428,75
quilogramas de alho e 1050 quilogramas diversos,
seria possível transportar toda essa carga de uma única
vez?
22) Um reservatório tem 6 metros cúbicos de
capacidade total. Em dado instante, o volume da água
existente corresponde à metade da sua capacidade.
Para escoar a água, existe uma válvula localizada na
base do reservatório e que escoa 0,02 metro cúbico de
água por minuto. Quanto tempo a válvula deve
funcionar para escoar toda a água que há no
reservatório?
Se houver excesso de carga, de quantos quilogramas
será esse excesso?
13) Um número x é tal que x = (51,7 + 8,36) – (16,
125 + 7,88). Determine o número x.
23) Calcule o número decimal expresso por (0,8 –
0,15 : 0,3)3 : 5,4 + (0,5)2.
Departamento de Ensino- DE
Coordenação Geral de Ensino – CGE
Curso: AGRICULTURA
Disciplina: Matemática Aplicada a Agricultura
Prof. Ediênio Farias
E-mail: [email protected]
24) Uma pipa de vinho enche 63 garrafas de 0,7 litro
cada uma. Quantas garrafas de 0,9 litro cada uma a
pipa pode encher?
25) Qual o 5 número da sequência: 40; 10; 2,5...?
26) No inicio do mês, Manoel estava com um saldo
devedor de R$ 158,61 e resolveu fazer três saques
seguidos de R$ 45,00 cada um. Logo depois recebeu o
salário, no valor de R$ 985,73. Como ficou o saldo de
Manoel? Represente essa situação com uma expressão
numérica e resolva-a.
27) Conheça os melhores em salto em altura e depois
responda:
29) Dê exemplo, quando existir:
a)
b)
c)
d)
e)
Um número inteiro que não é natural.
Um numero natural que não é racional.
Um número que não é racional.
Um número racional que não é inteiro.
Um número racional que não é real.
30) Indique e calcule:
a) O produto de – 1,2 e + 0,6;
b) O quociente de – 1,2 por + 0,6;
c) A soma de – 1,2 e + 0,6;
Eles têm a fooorça!
d) A diferença entre – 1,2 e + 0,6;
Animais, que conseguem saltar mais que o homem,
concentram maior potência muscular nas patas
traseiras.
31) Descubra o segredo e encontre o valor da
expressão A + B – C + D.
 Puma: salta de uma altura de 9 metros sem se
machucar;
 Canguru: 3,50metros;
 Cavalo: 2,47 metros;
 Homem: 2,45 metros
 Tigre: 1,80 metros;
 Gato: 1,00 metro
 Pulga: 0,25 metro;
a) o salto do canguru é quantas vezes maior que
o salto do gato?
b) Quanto o homem consegue pular a mais que a
pulga?
c) Em um zoológico, o abrigo do tigre tem 2,18
metros de profundidade. Esse tigre
conseguiria pular para fora?
28) Escreva os números seguintes em notação
cientifica:
a) Urano é o sétimo planeta do Sistema Solar e
sua distância média do Sol é de 2 870 000 000
km;
b) Uma molécula chega a ter um diâmetro de
0,00000018 mm;
c) A distância da Terra ao Sol
aproximadamente 150 000 000 km;
é
- 3,12
C
-2,6
- 1,3
D
A
2
B
-1
-0,3
32) Pedro foi ao banco pagar algumas contas: a de
energia elétrica R$ 193,47, a de água de R$ 48,57 e a
de gás de R$ 34,89. Sabendo que Pedro levou ao
banco a quantia de R$ 300,00, quanto Pedro recebeu
de troco após pagar as três contas?
33) Qual 6º número da sequência: 1000; 100; 10...?
34) Que número devemos multiplicar por – 1,908 para
obter o seu oposto?
35) Que número devemos dividir – 15,07 para obter +
1?
36) O que sai mais barato: levar um amigo duas vezes
ao cinema ou levar dois amigos uma vez ao cinema?
de
d) O átomo de hidrogênio tem massa de
0,0000000000000000000000017 g.
37) Qual o oposto do oposto do módulo de – 6?
Departamento de Ensino- DE
Coordenação Geral de Ensino – CGE
Curso: AGRICULTURA
Disciplina: Matemática Aplicada a Agricultura
Prof. Ediênio Farias
E-mail: [email protected]
38) Considerando os valores reais atribuídos às letras
A, B e C, abaixo:
A = 2,54
B=–4
C=2
Tipo de lanche
Determine as operações seguintes:
a) A . B . C
b) AC
41) Calorias (cal) é uma unidade de medida de
energia. Examine o quadro abaixo e responda:
c) A:B – B.C
39) O 1 é o início de tudo!
Você pode escrever qualquer número racional,
“pequeno” ou “grande”, usando apenas o 1. Veja
alguns exemplos:
 5 = 1 + 1+ 1 + 1 + 1
 1 000 = 1 + 1 + ...+ 1 + 1 (um mil de vezes)
 vezes)
 0,5 = ½ ou 1 : (1 + 1)
 0,1 = 1/10 ou 1: (1+ 1+ 1+ 1+ 1 + 1+ 1+1 + 1+ 1)
Agora é com você. Escreva alguns números
racionais usando apenas o 1.
Peito de peru light
Hambúrguer simples
Hambúrguer duplo
X-salada
a) Que lanches diferentes uma pessoa pode comer
em um dia sem ultrapassar 1 200 cal?
b) Cite o nome de dois lanches tal que um deles
tenha, aproximadamente, o dobro de calorias
que o outro.
c) Qual lanche possui quase quatro vezes o número
de calorias que o sanduíche de peito de peru
light?
40) Números cruzados com decimais
(Use cada quadrinho para colocar o número ou a
vírgula)
42) Arroba:
unidade de
medida de massa.
Horizontais:
B: √144
D: 57,3 + 4,8
F: 6 : 5
G: (23)3
1 arroba vale,
aproximadamente,
14, 688 kg
Nos
cálculos,
usaremos: 1 arroba
= 15 kg
(O açougue, obra de Annibale Carracci)
Verticais:
A: 192
B: (1,1)2
C: 37,7 – 16,7
E: 11 : 4,4
A
D
José comprou 18 arrobas de carne para seu açougue e
pagou R$ 375,25 a arroba. Depois vendeu toda a
carne por R$ 30,00 o quilograma (kg). Qual foi o
lucro de José nessa venda?
B
E
F
Quantidade de calorias
(cal)
194
296
587
738
C
42) Velocidade média
Quando dizemos que um carro percorreu 240 km em 3
horas, podemos também dizer que sua velocidade
média foi de 80km/h.
a) Quantos quilômetros percorre um carro com
velocidade média de 90 km/h em 3 h 30min?
G
b) Quanto tempo gasta um carro para percorrer
340 km com velocidade média de 85 km/h?
Bom estudo!