Leis da ótica Experimentos com laser Telescópios

1
Leis da ótica
Experimentos com laser
Telescópios
Jair Barroso Junior/ON/MCT-2010
[email protected]
Introdução [Veja os Adendos no final; eles estão vinculados às figuras com um *]
O objetivo da presente palestra é mostrar/materializar com um laser como a luz se comporta
(propagação retilínea) ao encontrar os componentes óticos de um telescópio e ser utilizada
na região focal do mesmo. Um aquário comum é o veículo inicial onde serão mostradas as
leis básicas da refração e da reflexão da luz. Lentes e espelhos diversos compõem a
apresentação e são destacados os parâmetros essenciais para o entendimento do
funcionamento ótico dos telescópios. Imagens projetadas na tela durante os experimentos
permitem a comparação imediata com a teoria. Para complementar o assunto, é visto como
a difração da luz (propagação ondulatória) opera na formação das “imagens” estelares.
Nota: A primeira apresentação com laser relacionada com o assunto em pauta se deu, em
1983, como atividade paralela à Reunião da SAB em Itajubá. Versões mais recentes foram
apresentadas em mini-cursos para professores da CESAB–2001 (Águas de São Pedro),
2003 (São Pedro) e 2007 (Passa Quatro), as duas últimas com a configuração laser rotativo.
1.Refração da luz/superfície plana
Refração é o desvio que sofre a luz ao atravessar meios (transparentes) diferentes.
Exemplo: ar/água (no aquário), ou vice-versa.
Índice de refração é o parâmetro que mede a capacidade refringente de um meio.
Numericamente é o quociente da velocidade da luz no vácuo e no meio.
Alguns índices de refração: ar (1,00), água (1,33), vidro de janela (1,50), vidro flint (1,75),
diamante (2,50).
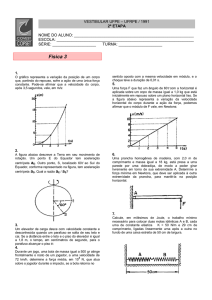
Na figura, N1PN2 é a normal (perpendicular) à
superfície S em P, ponto de incidência. AP é
o raio incidente e PB é o refratado.
O ângulo de incidência APN1= i, medido em
relação à normal, foi adotado arbitrariamente
como~ 45º.
O ângulo de refração BPN2= r é da ordem de
32º
e
foi
obtido
pela
relação
n1 sen i = n2 sen r, conhecida como lei de
Snell, com n1= 1,00 (ar) e n2= 1,33 (água).
(*1)
Fig1. Refração do raio AP ao encontrar a superfície S de separação de meios diferentes.
1
2
2. Reflexão da luz/ superfície plana
É o desvio simétrico que ocorre, num mesmo meio em relação à normal, quando a luz
encontra a superfície refletora.
Na figura, PN é a normal à superfície S no
ponto de incidência P, AP o raio incidente
e PB o refletido.
No caso da separação ar/água parte da luz
(96%) penetra na água e parte é refletida
(4%); a reflexão obedece à lei i=r.
Quando a superfície é polida (vidro, por
ex.) e possui uma finíssima deposição
superficial de alumínio ou prata, não há
refração e a reflexão pode chegar perto de
100%.
(*2)
Fig 2. Reflexão do raio AP ao encontrar a superfície S.
3. Refração da luz em lentes
As lentes mais espessas no centro do que nos bordos têm a propriedade de tornar
convergente um feixe de luz paralelo incidente. São chamadas de convergentes.
As que têm os bordos mais espessos que o centro tornam um feixe paralelo divergente. São
chamadas de lentes divergentes.
a. No exemplo que segue usamos uma
lente plano-convexa, convergente.
O raio AP1 foi traçado paralelo ao eixo
VC da lente L. No ponto P1 vale a lei
da refração em relação à normal CP1N
à superfície da lente. Os índices foram
admitidos n1= 1,00 e n2= 1,50.
P1 P2 sai como P2B, quando se tornou a
aplicar a lei de Snell, aqui, do vidro
para o ar.
C é o centro de curvatura da superfície
curva da lente e P2D, normal à
superfície plana, é paralelo ao eixo.
(*3)
Fig 3a. Caminho do raio AP1 incidindo na lente L.
2
3
b. No exemplo que segue usamos uma lente plano-côncava, divergente.
AP1 foi traçado paralelo ao eixo VC.
AP1 não sofre desvio pois é perpendicular à
superfície plana de entrada. Aplicando-se a
lei de Snell, acha-se r =90º .
P1P2 sai como P2B, afastando-se da normal.
C é o centro de curvatura da superfície curva
da lente e AP1 a própria normal à superfície
plana.
Fig. 3b. Caminho do raio AP1 incidindo na lente L.
4. Reflexão da luz em espelhos curvos
a. Côncavos esféricos.
Como a separação ar/vidro permite uma reflexão parcial, basta inverter o sentido do raio
P2B da figura 3b e teremos caracterizado o comportamento da luz nesse caso. Fica como
exercício a visualização do raio refletido; a normal é P2C .
b. Convexos esféricos
Nesse caso podemos utilizar a figura 3a e refletir AP1 em relação à normal P1N à superfície
convexa da lente. Fica também como exercício.
5. Foco, distância focal e plano focal
Imagens de objetos afastados
a. Lentes convergentes
As lentes reais possuem aberrações não consideradas aqui neste momento.
Numa lente convergente ideal, de espessura desprezível e sem aberrações, raios paralelos
ao eixo, como os provenientes de um objeto muito afastado, concentram-se num ponto do
eixo após atravessarem a lente. Tal ponto é o foco da lente e a imagem daquele objeto.
A distância desse ponto à lente é em primeira aproximação a distância focal da lente.
A figura 4a mostra, além disso, o que ocorre com raios paralelos provenientes de um ponto
afastado, porém incidindo com um ângulo a em relação ao eixo. A nova imagem P estará
num plano perpendicular ao eixo passando pelo foco F, definindo o plano focal da lente.
3
4
Como exemplo prático imagine-se o Sol e sua imagem gerada pela lente. A distância focal,
o tamanho da imagem e o plano focal ficam definidos de modo inequívoco.
(*4a)
Na figura, os raios centrais (paralelos ao eixo)
geram o foco F, enquanto que os inclinados de
um ângulo a com o eixo concentram-se em P no
plano focal.
PF é a imagem de um objeto afastado que
subtende um ângulo a em relação ao eixo.
Se a for da ordem de 30' e o objeto afastado
corresponder ao Sol, p.e., PF será sua imagem.
As imagens formadas nessas condições, no lado
oposto ao objeto em relação à lente, são ditas
reais.
(*4b)
Fig. 4a. Caracterizando alguns parâmetros de uma lente.
b. Espelhos côncavos (esféricos e parabolóides).
Estão representadas na mesma figura as seções planas parciais de dois espelhos. Na parte
superior um esférico de centro C e na inferior um parabolóide (de centro C para raios muito
próximos ao eixo), ambos representados por linha cheia grossa (a linha fina é da esfera).
O foco do esférico é considerado F1, que é
obtido para raios paralelos não muito afastados
do eixo CV1, vindos de um ponto objeto
distante.
Nota-se que, à medida que os raios se afastam
do eixo, o “foco” fica cada vez mais próximo
do vértice V1 do espelho.
Tal caracteriza a aberração esférica,
inconveniente fatal para muitas aplicações
astronômicas.
A seção parabólica goza da propriedade
evidenciada na figura. Qualquer raio paralelo
ao eixo converge sempre num foco único F2.
Fig. 4b. Esfera versus parabolóide.
(*4c)
4
5
Aqui se aplicam da mesma forma as definições anteriores de distância focal, no caso F1V1 e
F 2 V 2 , e a de plano focal (não representado), que, mesmo no parabolóide, é uma
aproximação às superfícies focais reais, em geral curvas.
O exemplo sugerido para o Sol (alto da pág. 4) se aplica aqui, da mesma forma, como no
caso das lentes convergentes.
6. Lupa
No caso mais simples as lupas são constituídas de uma única lente convergente, cuja função
é gerar uma imagem ampliada angularmente em relação à da visão direta do objeto pelo
olho, situado a uma distância convencionada de 25cm (ponto próximo). A imagem formada
é virtual (fica do mesmo lado do objeto em relação à lente), e não é invertida.
Na figura, o olho vê o objeto o sob
um ângulo a a 25cm de distância,
que é considerada a distância
mínima de visão distinta (nítida)
para um adulto de visão normal.
Quando interpomos a lupa entre o
olho e o objeto, com este entre a lupa
e seu foco, passamos a ver sua
imagem sob um ângulo b maior do
que o ângulo a.
O aumento angular é dado por b/a.
Esse aumento é da ordem de 25cm/f
quando a imagem se forma no
infinito e da ordem de 1+(25cm/f)
quando a imagem está no ponto
próximo, sendo f a distância focal da
lupa em centímetros. (*5)
Figs 5 a,b. Como o olho vê angularmente o objeto sem e com lupa.
7. Telescópios
Com o que vimos anteriormente já podemos entender o funcionamento dos telescópios, que
são constituídos de duas partes óticas. A objetiva ou coletor cuja função é receber a luz de
um objeto distante e concentrá-la numa região (focal) na forma de uma imagem real, e
(classicamente) a ocular, que permite o exame dessa imagem por nosso olho.
Usam-se também outros detetores de características diferentes da do olho – emulsões
fotográficas e CCDs, que permitem registrar as imagens de forma mais ampla e eficiente
usando diretamente a imagem focal. Nós os veremos adiante, fisicamente inclusive.
5
6
a. Telescópios refratores (lunetas)
A não ser nos instrumentos muito simples que usam apenas uma lente como objetiva, as
chamadas lunetas astronômicas têm usualmente a objetiva constituída por duas lentes,
uma de crown e a outra de flint, que geram imagens com aberrações reduzidas.
A objetiva convergente desses refratores, na maior parte das vezes, tem a distância focal
grande em relação ao diâmetro, razão da ordem de 15, que se escreve F/D=15.
As oculares, que funcionam como lupas, também são usualmente compostas de duas
lentes para corrigir aberrações, sendo os tipos clássicos as de Huygens e as de Ramsden.
Fig. 6 a. Diagrama simplificado de um refrator.
O trajeto dos raios é da esquerda para a direita.
Na figura 6a a objetiva, de distância focal F, é representada por OB e a ocular, de
distância focal f, por OC. Os raios paralelos ao eixo têm foco em A e os inclinados em
relação ao eixo concentram-se em B, gerando uma imagem focal AB invertida em relação
ao objeto.
A ocular funciona como lupa permitindo a ampliação de AB vista pelo olho, que deve
estar colocado na pupila de saída PS, imagem da objetiva formada pela ocular. A
ampliação angular, aumento do telescópio refrator, é dada por b/a=F/f.
b. Telescópios refletores
b1. Newtoniano
O coletor de luz (objetiva) de um telescópio newtoniano é um espelho côncavo de 1ª
superfície, muitas vezes esférico e nesse caso de razão F/D>10, valor que permite a
presença de aberração esférica não danosa para as imagens próximas do eixo. F/D é a
razão entre a distância focal e o diâmetro do telescópio. (*6)
O foco primário de um espelho côncavo é inaccessível praticamente à observação com o
olho por razões óbvias, daí Newton (1671) ter colocado um pequeno espelho plano
(chamado diagonal) a 45º com o eixo, que desvia lateralmente o feixe de luz tornando-o
utilizável em geral, seja pelo olho ou por outros detetores.
6
7
Fig. 6b1. Trajetos óticos de interesse num telescópio newtoniano.(*7)
Na figura, que repete em parte a 6a, o feixe paralelo ao eixo do espelho principal EP tem
sua imagem primária em A; um feixe inclinado em relação ao eixo de um ângulo a forma
em B uma imagem primária, porém de um ponto infinitamente afastado naquela direção.
O espelho plano secundário de 1ª superfície ES reflete aqueles feixes transferindo a
imagem AB para A'B', imagem real que pode ser utilizada da mesma forma que no
refrator por um detetor conveniente.
Obs. Os espelhos não apresentam aberração cromática como as lentes e, admitindo que o
primário seja um parabolóide, a imagem disponível A'B' poderá ser pouco afetada de
aberrações geométricas significativas.
O espelho secundário provoca uma obstrução do feixe luminoso que atinge o primário,
inevitável nessa configuração.
b2. Cassegrain
O coletor é um espelho côncavo usualmente parabolóide. Diferentemente do newtoniano,
que opera com baixa relação F/D (típico: F/D=6), o Cassegrain é usado comumente a
F/D>10. Para manter curto o instrumento, Cassegrain, por volta de 1672, idealizou uma
forma em que o feixe refletido no espelho côncavo voltasse em sua direção e, através de
um furo central de tamanho conveniente concentrasse a imagem focal fora do primário
côncavo. Tal foi conseguido interpondo um espelho convexo no trajeto do feixe refletido
pelo primário.
7
8
Fig. 6b2. Configuração ótica cassegrain.
A figura apresenta simplificações tendo em vista que algumas partes podem ser tomadas
da 6a e da 6b1. Fica a título de exercício esboçar o trajeto de um feixe inclinado em
relação ao eixo e localizar a imagem do ponto focal desta direção.
Como no newtoniano, a obstrução central traz uma perda inevitável da luz que chega no
telescópio.
8. Detetores
O olho humano é o detetor natural que possuímos e vem sendo usado há milênios nas
observações
do
céu,
inclusive
na
era
telescópica,
desde
Galileu.
Comparação câmara fotográfica/olho, uma pequena digressão.
• a pupila representa o diafragma que controla a quantidade de luz que penetra no olho,
• o cristalino, de distância focal variável, representa a objetiva da máquina, sendo capaz
de ajustar seu foco, ao invés de se movimentar como a objetiva, para pôr a imagem na
retina.
• a retina corresponde ao filme nas máquinas clássicas e ao CCD nas câmaras digitais,
• a resolução espacial, através do mosaico de cones e bastonetes da retina, corresponde à
granulação do filme fotográfico ou à rede de pixels do CCD.
Placas fotográficas e CCDs dispensam em princípio o uso de oculares e registram
diretamente as imagens focais dos instrumentos descritos.
Nota: É apresentada usualmente, ao vivo, aos alunos/professores, além de componentes
óticos usados nas demonstrações:
uma câmara fotográfica de fole, que usa um filme sensível à luz como detetor, e que
serve para a visualização comparada com os componentes do olho .
A figura que segue foi extraída de Basic Optics and Optical Instruments/Dover.
8
9
9. Difração nas objetivas dos telescópios
( leitura opcional )
Considerando a luz como onda pode-se mostrar que a “imagem” de uma estrela no foco
de um telescópio é constituída de um disco brilhante cercado de anéis escuros e claros
que se dissipam à medida que se afastam do centro (fig.7, à direita). Tal é o efeito
produzido quando a frente de onda da luz emitida pela estrela encontra a objetiva. Quase
toda a luz incidente na objetiva se concentra no disco de difração. O disco, visto do
centro da objetiva, subtende um ângulo que, segundo a teoria, depende inversamente do
diâmetro da objetiva. Aumentando então o diâmetro da objetiva, esse ângulo diminui e,
se mantivermos a distância focal do telescópio, o disco físico de difração será menor. Isto
tem conseqüências importantes, mormente quando se estuda o poder separador dos
telescópios, capacidade que têm de mostrar objetos muito próximos angularmente.
9
10
Por outro lado, mantendo o diâmetro mas aumentando a distância focal do telescópio
(F/D maiores), estaremos aumentando o tamanho físico do disco de difração.
Fig. 7. Imagem de difração de uma estrela e distribuição da luz no plano focal.
O perfil superposto à direita do plano focal AB representa a distribuição da luz na figura
de difração. O ângulo a corresponde ao raio do disco e vale aproximadamente 14cm/D
em segundos de grau, com D medido em centímetros, para a luz de λ (comprimento de
onda) = 0,55μm .O raio físico do disco, AB, nas mesmas condições vale 0,67μm x ( F/D).
Esses parâmetros são importantes quando se deseja ver (resolver) duas estrelas
angularmente muito próximas no céu. Se elas estiverem a uma distância angular da
mesma ordem que a (raio angular do disco) poderão ser vistas em princípio separadas.
Na prática quando se tenta ver ou registrar tal situação limite através de detetores
acoplados a um telescópio (baseado na Terra), mesmo provido de uma ótica
excepcionalmente boa, as coisas se complicam. Quem responde por isso em geral é a
atmosfera terrestre devido aos movimentos do ar, principalmente os turbulentos, que
deformam a frente de onda que chega ao coletor. A imagem que se observa ou registra
normalmente está longe do que a teoria da difração prevê. Contorna-se isto colocando,
por exemplo, telescópios em órbita da Terra fora da atmosfera - este é o caso do Hubble e
do Hipparcos. Há ainda outras soluções envolvendo tecnologias específicas, não só para
corrigir as distorções das imagens causadas pela atmosfera antes da luz chegar ao detetor
final (ótica adaptativa), como as que permitem alterações na superfície dos próprios
espelhos dos telescópios para preservar sua forma em operação (ótica ativa).
10. Referências
Impressas
a. Em português (traduções)
• Física do Francis Sears, vol.3, Ed. Ao Livro Técnico.
Conceitos básicos e cálculos envolvendo os principais parâmetros geométricos que se
relacionam com lentes, prismas e espelhos, isoladamente ou combinados.
A luz é tratada como onda também.
10
11
• Física do Paul Tipler, vol.2, Ed. Guanabara Dois
Apesar do enfoque ser o da luz como onda, há um capítulo, o 27, que mostra as principais
equações da ótica geométrica e que permitem os cálculos dos parâmetros de interesse
numa aproximação boa para uma introdução.
b. Em inglês
• Basic Optics and Optical Instruments da U.S. Navy, Ed. Dover Publications
Em parte tem o conteúdo essencial dos anteriores, mas apresenta um número inusual de
excelentes ilustrações, inclusive fotos, mostrando os trajetos da luz nos componentes dos
instrumentos de ótica aqui considerados.
Obs. Aparentemente não há restrições de cópia para uso não comercial. Possuo a obra.
Site na internet
http://www.feiradeciencias.com.br/sala09/index9.asp
Veja os itens Espelhos Planos e Espelhos Esféricos para começar.
Programa de traçado ótico
Optics Lab da Science Lab Software.
È um programa que permite projetar e desenhar na tela o trajeto de raios de luz em
sistemas óticos envolvendo lentes e espelhos.
Interposição de lentes e espelhos esféricos num cilindro de luz laser
Para gerar um tubo de luz laser utilizei uma montagem como a esquematizada em corte
na figura 8, em que T é um cilindro de material leve (alumínio) fixado na bucha B; nela
passa o eixo E de um ventilador M (tipo residencial de mesa) do qual removemos as pás.
O cilindro é sulcado externamente para acomodar e alinhar o laser L e o contra-peso C,
que são presos ao cilindro por braçadeiras. O controle de velocidade do motor é feito por
meio de um dimmer para ventilador fazendo-o girar em baixa rotação (~300 rpm). O
elemento difusor do laser pode ser água dispersada por um atomizador de molhar plantas;
melhor usar uma máquina de fumaça de show. O diâmetro do feixe cilíndrico utilizado
foi da ordem de 75mm, inferior ao diâmetro dos elementos óticos que utilizei no
experimento. Usando lentes convergentes ou espelhos esféricos côncavos interpostos no
feixe cilíndrico é imediato ver a formação do feixe cônico e o foco do elemento.
11
12
Fig. 8. Montagem do laser rotativo.
Adendos ao texto principal: lembretes, comentários, sugestões, exemplos e
experimentos, marcados no texto com (*), são inseridos usualmente durante uma
apresentação aproximada de duas horas.
(*1) Item 1. pág. 1
Refração da luz dos astros na atmosfera terrestre
A atmosfera terrestre pode ser considerada, numa aproximação conveniente, como
constituída por uma série de camadas paralelas de densidade (índice de refração)
crescente de seu exterior até o solo. Cada vez que a luz proveniente de uma estrela, por
ex., passa de uma camada para a seguinte ela sofre um desvio de acordo com a lei de
Snell, aproximando-se da normal, até nós a vermos mais elevada do que está
geometricamente; a única exceção é quando a estrela está no zênite. Com isto, as
observações de altura dos astros precisam ser corrigidas adequadamente, pois suas
distâncias zenitais aparecem menores do que as que teriam sem a presença da atmosfera,
tendo-se então que aplicar uma correção aditiva à distância zenital para situá-los na
posição geometricamente correta; quanto mais baixos maior o desvio, maior a correção.
Exemplo notório de refração diferencial: Sol ou Lua Cheia baixos no horizonte
Bem perto do horizonte, as diferenças de correção devidas à refração da luz na atmosfera
são grandes o bastante para deformar consideravelmente a imagem que vemos do Sol, ou
da Lua Cheia, que ficam parecendo achatados. Considerem-se os extremos de diâmetros
verticais para entender melhor.
(*2) Item 2. pág. 2
Reflexão total. ( laser no aquário)
Nota: Em todas as demonstrações, em ambiente preferencialmente escuro, usamos meios
difusores a fim de obter uma visão melhor do feixe de laser (vermelho, de He-Ne, ou
verde, de Nd). Uma quantidade pequena de maisena caseira na água do aquário e fumaça
(etileno-glicol) ou água atomizada funcionam satisfatoriamente na parte aérea.
12
13
Admitindo a parede do aquário de espessura desprezível, pode-se apreciar bem o
comportamento do raio, encostando o laser quase verticalmente numa parede lateral do
aquário e o apontado de baixo para cima de modo que a luz atinja a superfície líquida.
Veremos inicialmente que o raio sai do aquário, mas, à medida que diminuímos a
inclinação do laser o raio refratado fica cada vez mais rasante à superfície líquida, e, a
partir de um dado ângulo, o raio atinge a superfície e retorna para o interior (fundo) do
aquário, caracterizando a reflexão total.
Desvio lateral em lâminas de faces paralelas. (paredes paralelas no aquário)
As faces opostas do aquário (as maiores de preferência) servem para mostrar que a luz do
laser sofre um desvio ao incidir numa face e, depois de atravessar a água, sai
paralelamente à direção original na face oposta. A experiência é melhor apreciada
fazendo-se a incidência ocorrer horizontalmente, começando-se intencionalmente pela
incidência normal, quando não há desvio. A visão mais conveniente é feita com o aquário
no chão e observada de cima.
(*3) Item 3. págs. 2 e 3
Plano tangente a superfícies curvas, centro de curvatura e reta normal.
Uma folha de papel tocando uma esfera (de isopor, por ex.) caracteriza um plano tangente
à esfera naquele ponto de contato. Se cortarmos diametralmente a esfera por um plano a
seção será um círculo e a interseção desse plano com o plano tangente uma reta tangente
ao círculo (seção da lente), no ponto de contato. Nas figuras 3a e 3b esta reta tangente
está representada pelo traço forte, perpendicular ao raio de curvatura (normal à esfera de
centro C), no ponto de contato. Por simplicidade lidamos aqui com as seções planas.
(*4a) Item 5a. pág. 3
Demonstração prática com o Sol, usando um condensador de projetor fotográfico e
um anteparo para projeção da imagem.
Lupas (lentes de aumento) comerciais servem bem para mostrar a posição do foco. Se
quisermos ver melhor a imagem do Sol, teremos que utilizar uma lente convergente de
distância focal maior. Uma relação prática é de que a imagem do Sol tem diâmetro da
ordem de um centésimo da distância focal da lente. Exemplo: distância focal= 100mm,
imagem= 1mm de diâmetro; distância focal=100cm, imagem= 1cm de diâmetro, que já
dá para se ver bem.
Nunca olhe para o Sol por uma lente ou no foco de um espelho côncavo. Pode cegar!
(*4b) Item 5a. pág.4
Determinação de distâncias focais de lentes convergentes projetando imagens de
objetos distantes em anteparos (na parede da sala, por exemplo).
Melhor fazer a experiência num dia de Sol, com a janela aberta, e algum objeto da
paisagem exterior iluminado.
Coloca-se a lente paralela a uma parede (clara de preferência; senão, prende-se um papel
branco na parede) e se tenta, aproximando ou afastando a lente, obter uma imagem nítida
13
14
do que se visa no exterior (árvore, poste, casa, por ex.). A distância da lente à parede,
que pode ser medida com uma régua, é (em primeira aproximação) a distância focal da
lente. Nota-se que a imagem se mostra completamente invertida.
(*4c) Item 5b. pág. 4
Determinação de distâncias focais de espelhos côncavos projetando as imagens em
folhas de papel branco ou vegetal (espelho de toucador com o Sol, por exemplo).
Como a imagem formada por espelhos côncavos se situa do mesmo lado do objeto, há
que se usar algum expediente para ter acesso à imagem sem bloquear muito a luz
incidente no espelho. Pode-se, por ex., fazer um disco de papel bem menor que o
diâmetro do espelho, colá-lo na ponta de uma haste fina (palito de sorvete), e procurar,
como no caso da lente convergente, a imagem mais nítida (mais intensa) do Sol, que
definirá o foco do espelho. Espelhos de toucador têm usualmente um lado plano e o outro
côncavo, este com distância focal da ordem de 40cm, dando uma imagem do Sol de uns
4mm. Não se surpreenda com as aberrações (cáusticas) do espelho esférico.
(*5) Item 6. pág. 5
Uso do condensador de projetor fotográfico como lupa.
O condensador utilizado nos experimentos tem um diâmetro da ordem de 11cm e
distância focal de 16cm. Como sua área é grande permite um campo de visão grande se
comparado com lupas de pequeno diâmetro.
(*6) Item 7a. pág. 6
Diferença entre espelho comum e de primeira superfície.
O espelho de toucador citado anteriormente bem como a maior parte dos espelhos
comerciais têm a camada refletora (alumínio ou prata) na face posterior do vidro em
relação a quem olha, camada normalmente protegida por tinta ou verniz. Em geral a
reflexão na camada anterior passa despercebida por questão de contraste.
Nos instrumentos óticos que operam com espelhos (telescópios, por ex.) uma segunda
imagem não é aceitável. Nesse caso, usam-se espelhos de primeira superfície onde a
camada refletora se encontra na face anterior do espelho, a que recebe diretamente a luz .
(*7) Item 7b1. pág.7
Uso de prisma diagonal ao invés de espelho.
O desvio lateral necessário para a observação das imagens nos telescópios newtonianos, e
o que se usa próximo às oculares para observar-se mais comodamente em certas posições
dos telescópios, são obtidos por reflexão em espelhos planos. Pode-se obter o mesmo
resultado utilizando prismas de ângulo reto de catetos iguais, em que o eixo do feixe
incidente encontra uma face cateto perpendicularmente, refletindo a seguir na face
hipotenusa, esta a 45º com o eixo do telescópio; após a reflexão total na face hipotenusa o
feixe sai perpendicularmente à outra face cateto, na direção do observador.
Ação combinada reflexão, refração e dispersão da luz – arco-iris (rainbow)
Entre muitos sites na web sobre o asunto, veja, p.e.: http://eo.ucar.edu/rainbows/
14
15
15