LinkRadar

PROE - Radiação
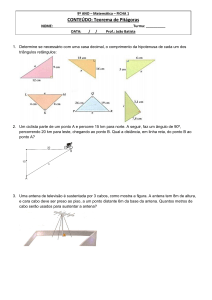
As duas áreas principais de aplicação das antenas são:
Links de comunicação
Radares
Consideremos um link de comunicações
emissor
receptor
Antena 1
Antena 2
P1 – Potência emitida pela antena 1
Qual é a parte da potência emitida P1 que a antena 2 consegue receber?
A potência total incidente na antena de recepção obtém-se integrando a “densidade de
potência” (Vector de Poynting) na “área efectiva” da antena de recepção.
A forma como a antena de recepção converte a potência que sobre ela incide em
potência disponível aos terminais da antena, depende do tipo de antena, da sua
orientação e polarização.
PL  SAeM
PL - potência média no tempo disponível aos terminais da antena 2, supondo que a
antena 2 (recepção) não tem perdas, está alinhada com a antena 1 de modo a
receber a potência máxima radiada pela antena 1 (isto é, tem o seu máximo do feixe
na direcção da onda incidente e a sua polarização está alinhada com a da onda
incidente).
S - valor médio no tempo da densidade da “densidade de potência” da onda incidente.
área / 
PL  SAeM  
2 
 m 


W 
W .m2 
AeM - área efectiva máxima. Mede a capacidade da antena em interceptar a onda
incidente. É uma medida da capacidade que a antena de recepção tem em converter
a potência incidente em potência disponível aos terminais da antena de recepção.
 I2
V 02
I2 
V 02
Z az  Z L
PL 
1 2
I 2 RL
z
ZL
~
Z az
Fig.1 – Circuito equivalente da antena de recepção
Z a 2  Ra 2  jX a 2 - impedância da antena de recepção
AeM - Supõe transferência máxima de potência da onda incidente para os terminais da
antena 2, isto é : Z L  Ra 2  jX a 2
I2 
V 02
V 02
V 02


Z az  Z L 2 Raz 2 Rr
Desprezamos perdas na antena 2:
P
1 V 02
Ra 2  R p  Rr  Rr    r  PL 
Paz
2 4 Rr
2
2
1 V 02
PL 
2 4 Rr
2
P
1 V 02
AeM  L 
S
2 4 Rr S
e
Exemplo DEH
Vamos calcular a abertura efectiva máxima do DEH, que traduz a capacidade máxima
que o DEH tem de intersectar a potência de uma onda incidente e entregá-la a uma
carga.
+l
L = zl << λ
-l
O DEH está orientado paralelamente ao DEH emissor e tem aos seus terminais uma
carga Z L  Z a*2
Tensão em vazio aos terminais do DEH2:
V 02  E 01 hefM  E 01 L
Potência da onda incidente: S 
he DEH  L sin 
2
1 Eoi
2 Z0
2  L 
Resistência de radiação: RrDEH  Z0
 
3 
z
2
2 L2
V02
Eoi
2 Z0
PL
3 2
AeM 




2
S 8 Rr S
8
 2  L 2 Eoi
8 Z0 

 3  
 
Área máxima efectiva:
AeM DEH  0.119 2
A área efectiva máxima do dipolo eléctrico de Hertz é independente do comprimento do
DEH.
Relação entre AeM e D ( directividade )
DDEH 
DDEH 
3 4 3 2


2 2 8
4
2
AeM
A relação anterior entre a directividade e a área (ou abertura) efectiva é uma relação
universal válida para qualquer antena.
Link de comunicação

Antena de emissão isotrópica:
U  r S  S   S   Ur
2
2

Pr
4 r 2
P1 - potência média no tempo radiada pela antena emissora

Antena não isotrópica com o máximo de radiação segundo a antena de recepção:
S
UM
D
r2
4
2

D Pr
4 r 2
AeM
Como se tem:
PL  S AeM 
D Pr
4 r 2
AeM
Supõe-se que a antena de recepção está apontada e tem uma polarização que conduzem
a uma recepção máxima.
AeM - abertura efectiva máxima da antena de recepção.
AeM 2 
D2
42
Como
D P
2
2
PL  1 1  D2
 P1 D1D2
4 r
4
4r 2
A fórmula anterior dá-nos o valor da potência recebida PL em termos da potência
transmitida P1 e das directividades das antenas de emissão D1 e de recepção D2 .
Como D1 
4
2
Ae M 1 tem-se: PL  P1
AeM 1 AeM 2
r 2 2
Fórmulas de
transmissão de Friis
(antenas sem perdas)
Perdas nas antenas
Na prática as antenas têm perdas e a potência radiada pela antena de emissão é reduzida
de  . Na recepção acontece o mesmo e a potência é também reduzida de um factor  .
Por isso utiliza-se o ganho G   D em vez da directividade
4
G  2  AeM
 
Ae
G
4
2
Fórmulas de transmissão
de Friis
(antenas com perdas)
Ae
PL  P1 G1 G 2
2
4r 2
As fórmulas anteriores pressupõem que não há desadaptação de impedância nos
terminais das antenas emissora e receptora e que as antenas de emissão e recepção têm
polarizações idênticas e estão orientadas de modo a haver adaptação de polarizações e
ganho máximo.
Se as condições anteriores de máxima recepção não forem satisfeitas as fórmulas de
Friis têm que ser corrigidas de modo a incluir os efeitos de:
1. desadaptação de polarizações
2. desadaptação aos terminais das antenas
3. desalinhamento entre antenas
As desadaptações vão reduzir a potência que é trasmitida à carga na recepção, o que se
traduz numa redução da abertura efectiva.
Desadaptação de impedâncias
A'e  Cq Ae
Z  Z az
Cq  1  k 2  1  L
Z L  Z az
k – módulo do factor de reflexão na carga
Z a 2 - impedância de entrada da antena 2
2
Cq :0;1
k  0  Cq  1
k  1  Cq  0
Desadaptação de polarizações
''
A  C p Ae
e
C p - Factor de desadaptação de polarizações ou eficiência de polarização
C p = 1 quando a onda incidente e a antena de recepção têm a mesma polarização.
C p = 0 quando as polarizações são ortogonais
Por ex: polarizações horizontal e vertical
Circular direita e circular esquerda
Para determinar C p usamos o conceito de altura efectiva da antena h definida como ;
__
__
~
~
V 02  h*  Ei
V02 - tensão em vazio aos terminais da antena 2 de comprimento efectivo h quando
incide na antena um campo Ei . O comprimento efectivo h contém informação sobre o
campo de radiação da antena e em particular sobre a sua polarização e pode ser ou não
um vector complexo.
No caso, por exemplo, de h e E serem ambos vectores lineares e paralelos, a tensão
aos terminais da antena de recepção é máxima.
Exemplo: DEH à emissão
__
^
Z e  jkr
Ei  j 0
I L sin  e
2 r
~
~
Z e  jkr
 j 0
I he
2 r
~
^
he  L sin  e
~
~
O comprimento efectivo de DEH é a projecção do comprimento físico “visto” segundo
cada ângulo  .
he
he
θ
he
θ
θ
Antena de recepção
A potência recebida é proporcional a:  V 02
2
2
*
h
~ e2
.E
~ i
O coeficiente C p ( 0  C p  1 ) traduz o facto de uma fracção da potência ser perdida
devido à desadaptação de polarizações entre a onda incidente e a antena de recepção.
2
h*  E
~ e2 ~ i
2
Cp 
he 2
Ei
2

h*
~ e2
he 2
__
Ei
 ~
2
Ei
Ei
representa o estado de polarização da onda incidente que coincide com a
Ei
polarização da antena de emissão no caso do meio não alterar esta polarização.
hˆe 2
- vectores complexos unitários do comprimento efectivo da antena de recepção e da
eˆ1
^
onda incidente.
Cp  h
^2
e
~ e2 ~
Aplicação
^
^
^
~
~
 cos 45 o x  j sin 45 o y
h
~ e2
Antena de recepção com polarização circular esquerda :

^
1  ^
x  j y
2  ~ ~ 
__
E
~i
Ei
^
^
~
~
e  y
Antena emissora com polarização vertical:
2
Cp 
^ * ^
1  ^
1
x  j y  y 

2
2  ~
~ ~
Metade da potência é perdida devido a desadaptação de polarizações.
Numa emissão com polarização linear e recepção com polarização circular, ou vice
versa, perde-se sempre metade da potência.
Esta situação é comum na comunicação com satélites por causa da ionosfera que altera a
polarização (Efeito de Faraday) durante o trajecto de propagação. Assim garante-se que
há sempre sinal na recepção embora com metade da potência.
Cálculo da perda de potência devido aos dois tipos de desadaptações:
PL ( dBm )  P1( dBm )  10 log C p  10 log Cq
RADARES
Consideremos que o alvo é um avião.
As antenas de emissão e recepção estão orientadas de modo a que a sua direção de
máxima radiação está apontada em cada instante para o alvo.
S1 
Pa1
PA
G1  12 e21
2
4 r
 r
A potência intersectada pelo alvo (avião) é proporcional à densidade de potência
incidente S1 .
PAlvo   S1
A constante de proporcionalidade tem as dimensões de uma área e designa-se por  secção eficaz do radar.
 é uma área equivalente do alvo (avião) como se este radiasse a potência de forma
isotrópica.
Na realidade, a potência incidente não é re-radiada pelo alvo de forma isotrópica. A
forma como a potência incidente é espalhada (“scattered”) pelo alvo não é importante
porque a recepção recebe apenas potência segundo uma direcção e estamos só
preocupados com o que acontece nessa direcção.
Assim a densidade da potência espalhada S scat surge como
P
S scat  alvo
4 r 2
No receptor a potência disponível será :
PL  Ae2 S scat
Combinando as equações anteriores obtém-se:
PL  Ae 2
PL  Pa1
G 
4
2
PL  Pa1
Como:
 S1
A A 
 Pa1G1 e1 4e 2 2
2
4 r
4 r 
Ae1 Ae 2
4 r 4 2
Ae
2G1 G2
4 3 r 4
Normalmente nos radares as antenas 1 e 2 são iguais, são iguais pelo que: G1 = G2 =G
Cálculo da secção eficaz do radar
PAlvo   S1
S scat 
Palvo
4 r 2
  4 r 2
Scat
S1
Isto é, a secção eficaz do radar é 4 vezes o cociente entre a densidade de radiação que
2
resulta de (potência espalhada) r Sscat na direcção do receptor e a densidade de
potência incidente proveniente da antena de transmissão, segundo a sua direcção de
máximo de radiação.
Alcance máximo do radar
Como a potência recebida cai com r 4 os sinais na detecção têm valores baixos da
relação S/N, o que exige o uso de receptores de elevada sensibilidade. Sendo a potência
mínima que o receptor pode detectar Pmin , o alcance máximo do radar será:
 P G 22 
Rmax   1

3
 ( 4 ) Pmin 
1/ 4
Com o processamento moderno é possível reduzir muito o valor de Pmin . Por exemplo
é usual integrar vários impulsos. Dado que o ruído tem média nula este procedimento
conduz a um factor de melhoria  N (sendo N – nº de impulsos).
Na prática há vários factores que diminuem o desempenho do radar:

Efeitos de propagação;

Interferências externas;

Natureza estatística do processo de detecção.