materiais elastoplásticos

MATERIAIS ELASTOPLÁSTICOS
-
DESCRIÇÃO DO COMPORTAMENTO ELASTOPLÁSTICO
Alguns elementos característicos dos ensaios de tração simples são analisados a
seguir para identificar os fenômenos que devem ser representados por um modelo
matemático de comportamento do material.
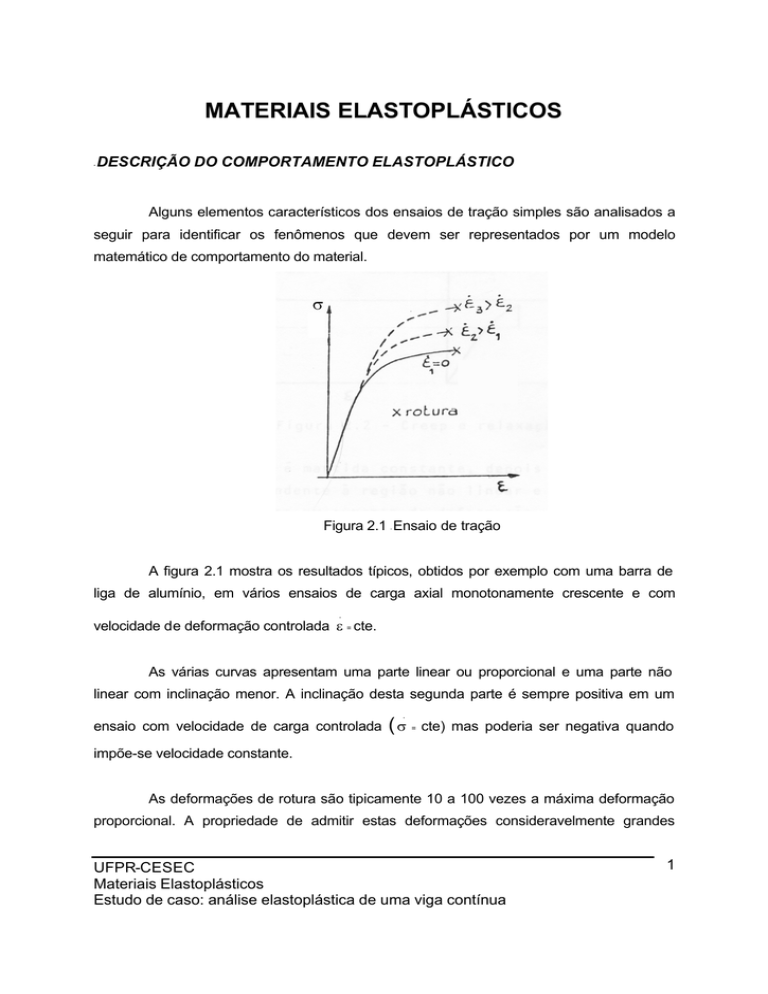
Figura 2.1 Ensaio de tração
-
A figura 2.1 mostra os resultados típicos, obtidos por exemplo com uma barra de
liga de alumínio, em vários ensaios de carga axial monotonamente crescente e com
.
velocidade de deformação controlada ε = cte.
As várias curvas apresentam uma parte linear ou proporcional e uma parte não
linear com inclinação menor. A inclinação desta segunda parte é sempre positiva em um
.
ensaio com velocidade de carga controlada
(σ
=
cte) mas poderia ser negativa quando
impõe-se velocidade constante.
As deformações de rotura são tipicamente 10 a 100 vezes a máxima deformação
proporcional. A propriedade de admitir estas deformações consideravelmente grandes
UFPR-CESEC
Materiais Elastoplásticos
Estudo de caso: análise elastoplástica de uma viga contínua
1
antes da rotura e chamada ductilidade. Quando o material tem pouca ductilidade, isto é,
rompe com pequena deformação, é chamado frágil.
.
A modificação da curva σ − ε com ε é uma característica do comportamento
.
viscoso, conseqüentemente dependente do tempo. Para ε muito pequeno tem-se o
processo de carga “estático”, que será utilizado para definir a relação tensão-deformação na
teoria de plasticidade independente do tempo.
Figura 2.2 Creep e relaxação
-
Se a tensão é mantida constante, depois de considerável deformação
correspondente à região não linear e durante um tempo prolongado, nota-se um aumento
da deformação. Este é o fenômeno de creep. Se em lugar disto, a deformação é mantida
constante apresenta-se a relaxação ou redução das tensões com o tempo.
.
Os fenômenos de alteração da curva σ − ε com ε , o creep e a relaxação são
manifestações do comportamento elastoplástico viscoso dos materiais reais que não serão
representadas nesta teoria restrita de plasticidade.
Se for executada uma série de ensaios de carga monótona até um valor qualquer
σ * seguida de um descarregamento monótono até zero, os resultados obtidos serão dos
dois tipos mostrados na figura 2.3 dependendo do valor da tensão σ * .
UFPR-CESEC
Materiais Elastoplásticos
Estudo de caso: análise elastoplástica de uma viga contínua
2
O valor de tensão σ * que distingue os dois comportamentos e a tensão de
escoamento inicial, ou limite de elasticidade σ Y . Qualquer processo de carga e
descarregamento com tensões (de tração) menores que σ Y é reversível no sentido de que
quando a tensão volta ao valor inicial também se reproduz o valor inicial da deformação.
Figura 2.3 Ensaios de carga e descarregamento
-
O comportamento plástico se distingue do elástico porque produz deformações
permanentes, ou seja, que é irreversível, e não pela falta de linearidade entre tensão e
deformação.
A medição da tensão de escoamento σ Y não é simples como se desprende da sua
definição. Desde o ponto de vista tecnológico σ Y é a carga que produz a menor
deformação permanente capaz de ser medida. A efeito de padronização se define a tensão
de escoamento convencional como a carga que produz uma determinada deformação
permanente pequena, geralmente igual a 0,002 (ou 0,2%).
Os valores de tensão limite de elasticidade, ou de escoamento e do limite de
proporcionalidade são bastante próximos para o aço e outros materiais de ampla aplicação.
Isto tem conduzido, às vezes, a confusões nestes conceitos de linearidade, elasticidade e
plasticidade.
Nos ensaios de carga e descarregamento que produzem deformação permanente
a plastificação somente ocorre durante o aumento de tensão. Apenas começa uma redução
de tensão os incrementos (negativos) de deformação são elásticos, isto é reversíveis ou
UFPR-CESEC
Materiais Elastoplásticos
Estudo de caso: análise elastoplástica de uma viga contínua
3
recuperáveis, aproximadamente proporcionais aos incrementos de tensão e com coeficiente
de proporcionalidade igual ao módulo de elasticidade E observado no início do
carregamento. Uma descrição cuidadosa do comportamento em carga e descarga seguidas
de um novo carregamento (Figura 2.4) apresenta um loop de histerese e uma concordância
suave na segunda carga. Estes detalhes são eliminados em uma descrição simples da
plasticidade.
Figura 2.4- Ensaio de carga, descarga e nova carga
-
Uma observação importante relativa a esta experiência consiste em identificar que
a tensão final do primeiro processo de carga σ * passa a ser o novo limite elástico no
carregamento que segue à descarga. Em outras palavras o processo de deformação
plástica modifica a tensão de escoamento inicial aumentando a faixa de comportamento
elástico em tração. Este é o fenômeno de encruamento ou endurecimento por
deformação plástica (work-hardening ou strain-hardening).
Outra experiência ilustrativa do comportamento de alguns materiais elastoplásticos
consiste em uma solicitação de tração seguida de uma descarga que produz plastificação
em compressão. Aqui fica aparente que a “resistência elástica” em compressão foi reduzida
pelo processo plástico de tração. Isto é, a deformação plástica de tração reduz a tensão de
plastificação em compressão enquanto aumenta a de tração pelo mesmo motivo. Este
fenômeno, chamado efeito Bauschinger implica no aparecimento de anisotropia no material
virgem isotrópico (σ Y + = − σ Y − ) já produzida pelo processo plástico.
0
0
UFPR-CESEC
Materiais Elastoplásticos
Estudo de caso: análise elastoplástica de uma viga contínua
4
Figura 2.5 Efeito Bauschinger
-
A descrição fenomenológica feita até aqui mostra que o comportamento plástico é
dependente do programa de carga mediante o qual se atinge um determinado nível de
carga. A deformação presente no material não é uma função da tensão atual unicamente,
senão que depende da história de carregamento anterior. Por exemplo na figura 2.6 os
pontos 1, 2 e 3 correspondem à mesma tensão mas a diferentes deformações em razão de
que esses estados terem sido alcançados mediante diversas histórias de tensão.
Analogamente os pontos 2 e 4 tem igual deformação com tensões diferentes.
Figura 2.6 Correspondência múltipla entre tensões e deformações
-
UFPR-CESEC
Materiais Elastoplásticos
Estudo de caso: análise elastoplástica de uma viga contínua
5
O material não lembra a parte da história do processo constituída de variações de
tensão e deformação puramente elásticos. Se diz então que a deformação é função da
história lembrada ou gravada. Este é então um material com memória evanescente e cuja
história lembrada deve ser representada pelos valores atuais de alguns parâmetros de
estado, por exemplo a própria deformação, a deformação permanente ou o trabalho plástico
dissipado. Estes parâmetros serão denotados nestas notas pelo símbolo h. O
comportamento depende da história no sentido que o valor destes parâmetros somente é
conhecido quando se tem a história do processo como dado. O valor destes parâmetros de
história lembrada h, somente é modificado em processos plásticos e permanece constante
em processos puramente elásticos.
Desde o ponto de vista puramente mecânico, isto é, sem utilizar conceitos
termodinâmicos não é possível medir deformações absolutas senão relativas a um estado
de referência acessível. Considere-se a experiência realizada por um observador que
recebe um material para ensaio que já foi plastificado anteriormente. Para este observador
o limite de plastificação inicial é diferente daquele que se obteria por exemplo, ensaiando a
peça recém fundida. Se as variáveis de estado termodinâmicas são incluídas poderia-se
definir um estado virgem do material.
Figura 2.7 Ensaio de tração de uma barra anteriormente plastificada
—
UFPR-CESEC
Materiais Elastoplásticos
Estudo de caso: análise elastoplástica de uma viga contínua
6
Outras aleações de alumínio e o aço doce mostram um comportamento diferente
em alguns aspectos ao descrito até aqui. O comportamento mostrado na figura 2.8,
correspondente à parte do processo em que a tensão permanece constante é chamado de
escoamento plástico.
Figura 2.8 Material perfeitamente plástico
—
Em certo sentido esta fase é análoga ao fluxo de um fluído, com a diferença de que
no fenômeno plástico a taxa de deformação não é uma função da tensão como acontece
nos fluídos. Veremos mais adiante que existem em plasticidade relações análogas às
equações
.
ε=
.
1
1
σ ou γ = τ
µ
µ
correspondentes a fluídos newtonianos porém com o parâmetro µ dependente do próprio
processo plástico e não apenas do material como no caso da viscosidade.
Este material que apresenta escoamento plástico tem uma tensão de plastificação
σ Y independente do processo plástico anterior e portanto independente da história
lembrada. Em conseqüência, não apresenta endurecimento por deformação nem efeito
Bauschinger.
O comportamento recém descrito conduz ao modelo de plasticidade ideal ou
perfeita, e aquele apresentado anteriormente ao modelo de plasticidade com
endurecimento ou encruamento.
UFPR-CESEC
Materiais Elastoplásticos
Estudo de caso: análise elastoplástica de uma viga contínua
7
2.2
-
MODELOS DE MATERIAIS ELASTOPLÁSTICOS
A análise das experiências descritas na seção 2.1 permite formalizar modelos para
representar o comportamento dos materiais elastoplásticos. A teoria de plasticidade que
será desenvolvida nas seções seguintes está baseada nas hipóteses restritivas
apresentadas a seguir.
i)
Independência em relação ao tempo - Admite-se que a deformação resultante de
uma história de tensões não depende da velocidade com que este programa se realiza.
Note-se que segundo este conceito o comportamento puramente elástico, em particular, é
independente do tempo pois é independente do próprio programa de tensões e
deformações anteriores.
O comportamento plástico aqui considerado é
então dependente da história
lembrada representada por valores de parâmetros de endurecimento que denotamos por h.
Em conseqüência, os fenômenos viscosos de dependência da curva tensão.
.
deformação com as taxas ε e σ , isto é creep, relaxação, etc., ficam excluídos deste
modelo.
Nesta teoria, o tempo entra nas equações apenas como um parâmetro capaz de
definir a ordem de precedência dos eventos. Se um determinado “tempo” é utilizado então
qualquer outro relacionado com este por uma função monótona crescente é igualmente
apropriado. As equações são então indiferentes a uma mudança de escala no tempo. O
único tipo de fluxo possível nestas condições é o escoamento plástico não viscoso
característico dos materiais idealmente plásticos. Com efeito, uma relação de tipo fluxo
viscoso newtoniano
.
ε=
1
σ
µ
pode ser integrada se µ for independente do tempo, e para σ constante como ocorre no
escoamento plástico, resultando em
ε (t ) = ε 0 +
.
1
σ (t )
µ
UFPR-CESEC
Materiais Elastoplásticos
Estudo de caso: análise elastoplástica de uma viga contínua
8
relação esta que não é indiferente à escala de tempo. No modelo que será desenvolvido, o
nível de tensão determina apenas se é possível que aconteça uma velocidade de
deformação. Em alguns casos particulares (von Mises) serão utilizadas relações do tipo
.
ε =σ µ
porém com µ dependente do processo e do tempo.
ii) Ductilidade ilimitada - As equações do modelo matemático de comportamento
elastoplástico em consideração não conterão informação que evidencie a rotura do material.
iii) Temperatura homogênea - Não serão considerados gradientes de temperatura no
corpo elastoplástico, nem a influência da temperatura na própria equação constitutiva do
material.
Finalmente vamos salientar novamente as características que distinguem a
plasticidade da elasticidade, em particular, a dependência da tensão como processo
plástico anterior e não somente com a deformação, assim como a irreversibilidade da
plastificação que evidencia-se no fenômeno observado de que variações infinitesimais
positivas de tensão (carga com plastificação) ou negativas (descarregamento elástico local)
devem ser relacionadas com as variações infinitesimais de deformação mediante módulos
tangentes diferentes. Conclui-se assim que uma teoria de plasticidade não pode ser uma
“teoria de deformação” que associa valores presentes de tensão e deformação, pois isto só
pode representar materiais elásticos, senão uma “teoria em taxas”, enunciada em termos de
taxas temporais de tensão e deformação.
UFPR-CESEC
Materiais Elastoplásticos
Estudo de caso: análise elastoplástica de uma viga contínua
9