soma 1 -próximo -"com os" -"formula 1"

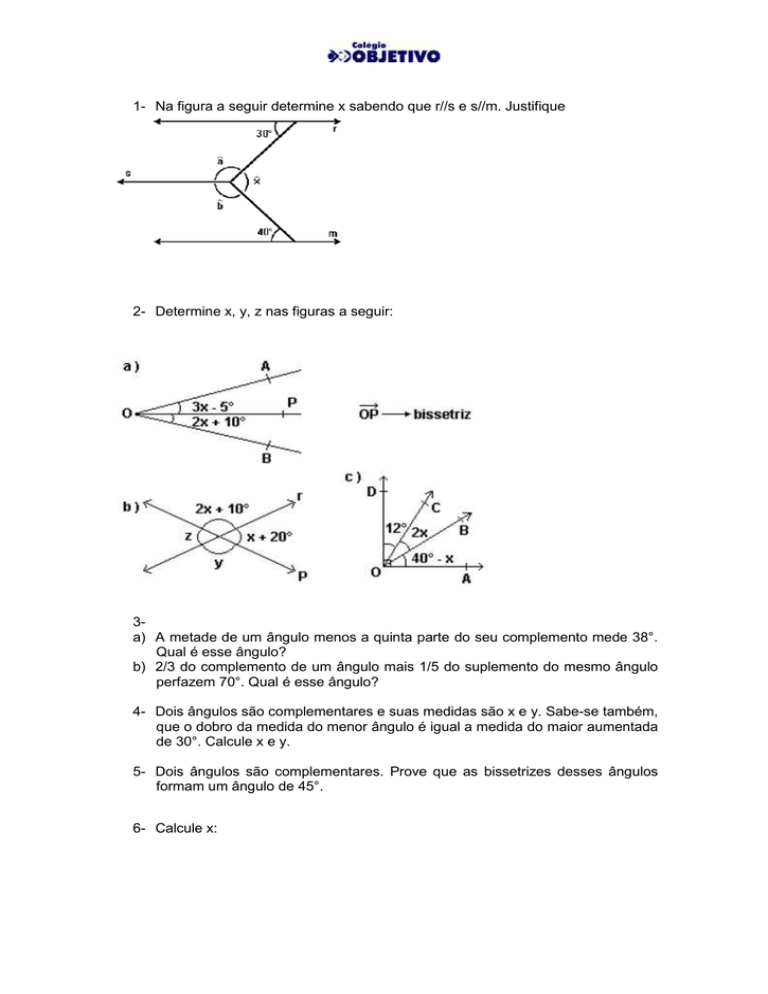
1- Na figura a seguir determine x sabendo que r//s e s//m. Justifique
2- Determine x, y, z nas figuras a seguir:
3a) A metade de um ângulo menos a quinta parte do seu complemento mede 38°.
Qual é esse ângulo?
b) 2/3 do complemento de um ângulo mais 1/5 do suplemento do mesmo ângulo
perfazem 70°. Qual é esse ângulo?
4- Dois ângulos são complementares e suas medidas são x e y. Sabe-se também,
que o dobro da medida do menor ângulo é igual a medida do maior aumentada
de 30°. Calcule x e y.
5- Dois ângulos são complementares. Prove que as bissetrizes desses ângulos
formam um ângulo de 45°.
6- Calcule x:
7- Dois ângulos são suplementares. Os 2/3 do maior excedem os 3/4 do menor
em 69°. Determine os ângulos.
8a) O que é um triângulo escaleno?
b) O que é um triângulo isósceles?
9- Os três ângulos de um triângulo têm para expressões respectivamente, 5x 40°, 2x + 20°, 3x. Verifique se este triângulo é equilátero.
10- (Ufsc) Na figura a seguir O é o centro da circunferência, o ângulo OÂB mede
50°, e o ângulo OïC mede 15°. Determine a medida, em graus, do ângulo OÂC.
11- (Unesp) Considere o triângulo ABC da figura adiante.
Se a bissetriz interna do ângulo B forma com a bissetriz externa do ângulo C um
ângulo de 50°, determine a medida do ângulo interno A.
12- Qual é o polígono convexo em que a soma dos ângulos internos é 1080°?
13- Determine x:
14- (G1) O ângulo interno de um polígono regular é o triplo do ângulo externo. Qual
é esse polígono?
15- A soma dos ângulos internos de um polígono regular é 1440°. Determine a
medida do ângulo central.
16- A medida do ângulo central de um polígono regular é 24°. De acordo com esta
informação, determine as seguintes medidas:
a) do ângulo interno.
b) do ângulo externo.
17- (Cesgranrio) Duas retas paralelas são cortadas por uma transversal, de modo
que a soma de dois dos ângulos agudos formados vale 72°. Então, qualquer
dos ângulos obtusos formados mede:
a)
b)
c)
d)
e)
142°.
144°.
148°.
150°.
152°.
18- (Cesgranrio) As retas r e s da figura são paralelas cortadas pela transversal t.
Se o ângulo B é o triplo de A, então B - A vale:
a)
b)
c)
d)
e)
90°
85°
80°
75°
60°
19- (Fuvest) Na figura adiante, as retas r e s são paralelas, o ângulo 1 mede 45° e
o ângulo 2 mede 55°. A medida, em graus, do ângulo 3 é:
a)
b)
c)
d)
e)
50
55
60
80
100
20- (Fuvest) As retas t e s são paralelas. A medida do ângulo x, em graus, é
a)
b)
c)
d)
e)
30
40
50
60
70
21- (Escola Técnica Federal - RJ) Duas retas paralelas cortadas por uma
transversal formam ângulos alternos-externos expressos em graus por 13x-8° e
6x+13°. A medida desses ângulos vale:
a) 31°
b) 3° ou 177°
c) 30° e 150°
d) 62°
e) 93°
22- Sabendo-se que a soma de dois ângulos é 78° e um deles vale 3/5 do
complemento do outro, os valores são:
a)
b)
c)
d)
10° e 68°
15° e 63°
16° e 62°
18° e 60°
e) 20° e 58°
23- O ângulo cujo suplemento excede de 6° o quádruplo do seu complemento, é:
a)
b)
c)
d)
e)
58°
60°
62°
64°
68°
24- (Pucpr) Dois ângulos complementares A e B, sendo A < B, têm medidas na
razão de 13 para 17. Conseqüentemente, a razão da medida do suplemento do
ângulo A para o suplemento do ângulo B vale:
a) 43/47
b) 17/13
c) 13/17
d) 119/48
e) 47/43
25- (Uel) A medida ‘ de um ângulo é igual ao triplo da medida do seu suplemento.
Nestas condições, tg‘ é igual a
a)
b)
c)
d)
e)
1
Ë2/2
0
- Ë2/2
-1
26- (Uel) Na figura a seguir, tem-se os ângulos XYW, XZW e XTW, inscritos em
uma circunferência de centro O.
Se med do ângulo XOW=80°, então med do ângulo XYW + med do ângulo XTW é
igual a
a) 160°
b) 150°
c) 140°
d) 120°
e) 100°
27- (Uff) O triângulo MNP é tal que ângulo M = 80° e ângulo P = 60°. A medida do
ângulo formado pela bissetriz do ângulo interno N com a bissetriz do ângulo
externo P é:
a)
b)
c)
d)
e)
20°
30°
40°
50°
60°
28- (Ufmg) Observe a figura.
Suponha que as medidas dos ângulos PSQ, QSR, SPR, assinalados na figura, sejam
45°, 18° e 38°, respectivamente. A medida do ângulo PQS, em graus, é:
a) 38
b) 63
c) 79
d) 87
29- (Unaerp) As retas r e s são interceptadas pela transversal "t", conforme a
figura. O valor de x para que r e s seja, paralelas é:
a)
b)
c)
d)
e)
20°
26°
28°
30°
35°
30- (Unirio) As retas r• e r‚ são paralelas. O valor do ângulo ‘, apresentado na
figura a seguir, é:
a) 40°
b) 45°
c) 50°
d) 65°
e) 130°
31- (Cesgranrio) ABCDE é um pentágono regular convexo. O ângulo das diagonais
AC e AD vale:
a)
b)
c)
d)
e)
30°
36°
45°
60°
72°
32- Seja ABC um triângulo isósceles de base BC. Sobre o lado AC deste triângulo
considere um ponto D tal que os segmentos AD, BD e BC são todos
congruentes entre si. A medida do ângulo BÂC é igual a:
a)
b)
c)
d)
e)
23°
32°
36°
40°
45°
33- (Ufc) Na figura a seguir, os segmentos de reta åæ, åè e èî são congruentes, ’ é
um ângulo externo, e ‘ um ângulo interno do triângulo ABD.
Assinale a opção que contém a expressão correta de ’ em termos de ‘.
a) ’ = 3‘.
b) ’ = 2‘.
c) ’ = ‘/2.
d) ’ = 2‘/3.
e) ’ = 3‘/2.
34- (Ufes) Um dos ângulos internos de um triângulo isósceles mede 100°. Qual é a
medida do ângulo agudo formado pelas bissetrizes dos outros ângulos
internos?
a) 20°
b) 40°
c) 60°
d) 80°
e) 140°
35- (Ufmg) Observe a figura.
Nessa figura, AB = BD = DE e o segmento BD é bissetriz de EïC. A medida de AÊB,
em graus, é
a) 96
b) 100
c) 104
d) 108
e) 110
36- (Ufrn) Na figura adiante, o ângulo š mede:
a) 94°
b) 93°
c) 91°
d) 92°
37- (Cesgranrio)
No quadrilátero ABCD da figura anterior, são traçadas as bissetrizes CM e BN, que
formam entre si o ângulo ‘. A soma dos ângulos internos A e D desse quadrilátero
corresponde a:
a) ‘/4
b) ‘/2
c) ‘
d) 2‘
e) 3‘
38- (Faap) A medida mais próxima de cada ângulo externo do heptágono regular
da moeda de R$ 0,25 é:
a)
b)
c)
d)
e)
60°
45°
36°
83°
51°
39- (Universidade São Francisco 95) O polígono regular cujo ângulo interno mede
o triplo do ângulo externo é o
a)
b)
c)
d)
e)
pentágono
hexágono
octógono
decágono
dodecágono
40- (Mackenzie) Os ângulos externos de um polígono regular medem 20°. Então, o
número de diagonais desse polígono é:
a)
b)
c)
d)
90
104
119
135
e) 152
41- (Puc-rio) Os ângulos internos de um quadrilátero medem 3x - 45, 2x + 10, 2x +
15 e x + 20 graus. O menor ângulo mede:
a)
b)
c)
d)
e)
90°
65°
45°
105°
80°
42- (Ueg) Na figura abaixo, para quaisquer que sejam x e y, as medidas dos
ângulos satisfazem a relação
a)
b)
c)
d)
y = 90° - x .
y = 180° - x .
y = 2x .
y = 3x.
43- (Unitau) O polígono regular convexo em que o n¡. de lados é igual ao n¡. de
diagonais é o:
a) dodecágono.
b) pentágono.
c) decágono.
d) hexágono.
e) heptágono.
44- (Fatec) Dada a figura:
Sobre as sentenças
I. O triângulo CDE é isósceles.
II. O triângulo ABE é equilátero.
III. AE é bissetriz do ângulo BÂD.
é verdade que
a) somente a I é falsa.
b) somente a II é falsa.
c) somente a III é falsa.
d) são todas falsas.
e) são todas verdadeiras.
45- (Universidade Federal ES)
Um polígono regular possui a partir de cada um de seus vértices tantas diagonais
quantas são as diagonais de um hexágono. Cada ângulo interno desse polígono mede
em graus:
a) 140
b) 150
c) 155
d) 160
e) 170
46- (Ufscar) Um polígono regular com exatamente 35 diagonais tem
a)
b)
c)
d)
e)
6 lados.
9 lados.
10 lados.
12 lados.
20 lados.
GABARITO
1. Como r//s, os ângulos x + 20° e (x/2) + 70° são
correspondentes. Assim, temos:
x + 20° = (x/2) + 70° => x = 100°
m e x + 20° = 120° são ângulos adjacentes
suplementares, logo
m + 120° = 180° => m = 60°.
2. x = 70°
3. a = 60° b = 120° c = 50° d = 130° e = 50°
4. a) x = 15° b) x = 50° ; y =110° ; z = 70° c) x =
38°
5. a) 80° b) 30°
6. x = 50° y = 40°
7. Observe a figura a seguir.
8. x = 170° 9. 36° e 144°
10. a) É todo triângulo que tem os três lados
diferentes.
b) É todo triângulo que tem dois lados iguais.
11. É eqüilátero 12. 25 13. 100° 14.
Octógono 15. x = 110°
16. Octógono. 17. 36° 18. a) 156° b) 24°
19. octógono e dodecágono
20. [B] 21. [A] 22. [E] 23. [E] 24. [A] 25.
[D]
26. [C] 27. c 28. [E] 29. [E] 30. [D] 31.
[C]
32. [C] 33. [B] 34. [A] 35. [B] 36. [C] 37.
[A]
38. [B] 39. [D] 40. [D] 41. [D] 42. [E] 43.
[C]
44. [D] 45. [B] 46. [B] 47. [B] 48. [E] 49.
[B]
50. [C]