5 lista Tubos e cordas

5º lista-Tubos e Cordas
1. (Ufpr 2017) Num estudo sobre ondas estacionárias, foi feita uma montagem na qual uma
fina corda teve uma das suas extremidades presa numa parede e a outra num alto-falante.
Verificou-se que o comprimento da corda, desde a parede até o alto-falante, era de 1,20 m. O
alto-falante foi conectado a um gerador de sinais, de maneira que havia a formação de uma
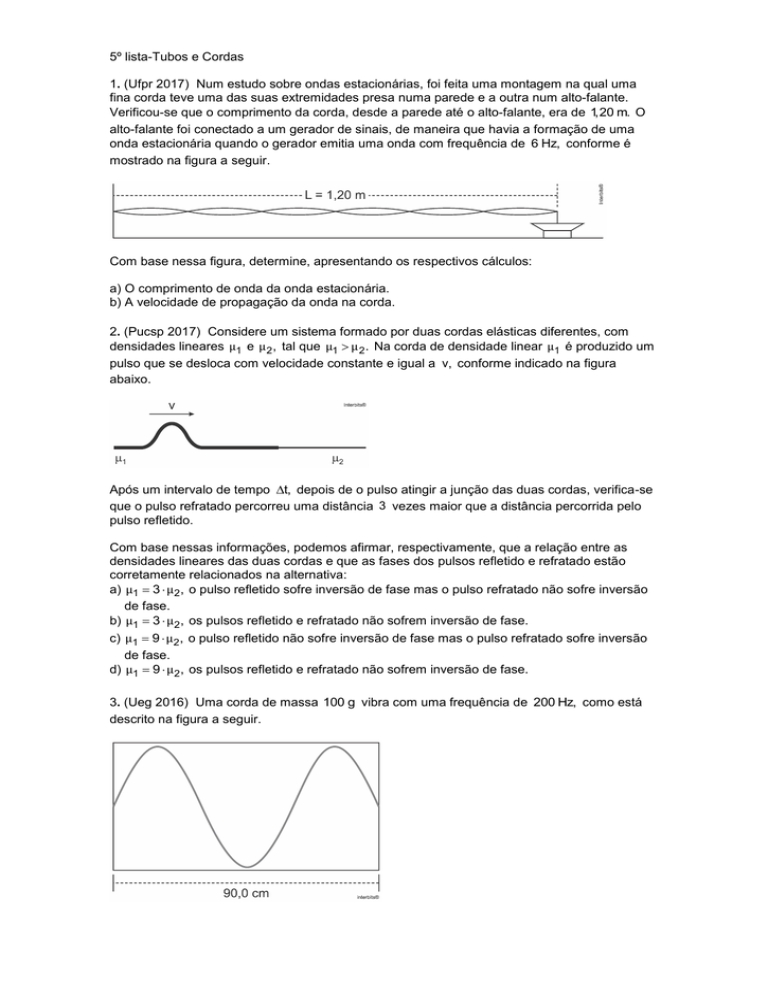
onda estacionária quando o gerador emitia uma onda com frequência de 6 Hz, conforme é
mostrado na figura a seguir.
Com base nessa figura, determine, apresentando os respectivos cálculos:
a) O comprimento de onda da onda estacionária.
b) A velocidade de propagação da onda na corda.
2. (Pucsp 2017) Considere um sistema formado por duas cordas elásticas diferentes, com
densidades lineares μ1 e μ2 , tal que μ1  μ2 . Na corda de densidade linear μ1 é produzido um
pulso que se desloca com velocidade constante e igual a v, conforme indicado na figura
abaixo.
Após um intervalo de tempo t, depois de o pulso atingir a junção das duas cordas, verifica-se
que o pulso refratado percorreu uma distância 3 vezes maior que a distância percorrida pelo
pulso refletido.
Com base nessas informações, podemos afirmar, respectivamente, que a relação entre as
densidades lineares das duas cordas e que as fases dos pulsos refletido e refratado estão
corretamente relacionados na alternativa:
a) μ1  3  μ2 , o pulso refletido sofre inversão de fase mas o pulso refratado não sofre inversão
de fase.
b) μ1  3  μ2 , os pulsos refletido e refratado não sofrem inversão de fase.
c) μ1  9  μ2 , o pulso refletido não sofre inversão de fase mas o pulso refratado sofre inversão
de fase.
d) μ1  9  μ2 , os pulsos refletido e refratado não sofrem inversão de fase.
3. (Ueg 2016) Uma corda de massa 100 g vibra com uma frequência de 200 Hz, como está
descrito na figura a seguir.
O produto da força tensora com o comprimento da corda, em N  m, deve ser de
a) 1200
b) 1440
c) 1800
d) 2400
e) 3240
4. (Fac. Pequeno Príncipe - Medici 2016) A figura mostra esquematicamente uma montagem
utilizada em aulas práticas de física para o estudo de ondas estacionárias em cordas. Um
gerador de sinal elétrico faz com que um oscilador mecânico produza ondas em uma corda
tracionada por uma massa suspensa. A amplitude de oscilação do eixo do oscilador é
independente da frequência e muito menor que a altura dos fusos. A roldana é considerada
ideal.
Sobre esse experimento, analise as seguintes afirmativas:
I. Se a distância entre o oscilador e a roldana for reduzida, a frequência para se obter uma
onda estacionária de mesmo número de fusos (ventres) que o mostrado na figura será maior
e o comprimento de onda será menor.
II. Se a massa suspensa for aumentada, o comprimento de onda do harmônico mostrado não é
alterado e a frequência de ressonância será maior.
III. Se a frequência do quarto harmônico for 600 Hz, a do quinto harmônico será 750 Hz.
IV. Todos os pontos da corda vibram com a mesma frequência e velocidade transversal.
V. A velocidade do deslocamento transversal de um ponto da corda será máxima nas posições
de cristas e vales.
Com relação às afirmativas, assinale a alternativa CORRETA.
a) somente as afirmativas II, III e IV estão corretas.
b) somente as afirmativas I, III e V estão corretas.
c) somente as afirmativas I, II e III estão corretas.
d) somente as afirmativas I, II, IV e V estão corretas.
e) somente as afirmativas II e IV estão corretas.
5. (Uece 2016) Considere duas cordas vibrantes, com ondas estacionárias e senoidais, sendo
uma delas produzida por um violino e outra por uma guitarra. Assim, é correto afirmar que nos
dois tipos de ondas estacionárias, têm-se as extremidades das cordas vibrando com
amplitudes
a) nulas.
b) máximas.
c) variáveis.
d) dependentes da frequência das ondas.
6. (Udesc 2016) A figura abaixo ilustra uma montagem experimental para estudo de ondas
estacionárias em cordas esticadas, retratando um dos harmônicos de onda estacionária
possível de ser gerada pelo experimento.
Para gerar ondas estacionárias, entre os pontos A e B, o experimento permite ajustes na
tensão da corda (controle manual), e na frequência de perturbação periódica (controle via
regulagem do motor).
Considere a montagem experimental retratada na Figura 4, o conhecimento sobre ondas
estacionárias, e analise as proposições.
I. As ondas estacionárias não são ondas de propagação, mas resultam da interferência entre
as ondas incidentes (propagando-se de A para B) e das ondas refletidas pelo ponto fixo B
(propagando-se de B para A). Portanto, em determinadas condições de ajustes de frequência
e tensão na corda, ocorrerá a ressonância e, consequentemente, a formação de harmônicos
de onda estacionária.
II. A densidade linear de massa da corda utilizada no experimento não interfere na geração das
ondas estacionárias, isto é, cordas mais espessas ou menos espessas, submetidas às
mesmas condições de perturbação e tensão, gerarão o mesmo harmônico de onda
estacionária.
III. Fixando a frequência de perturbação da corda, e partindo-se de um estado de ressonância,
é possível atingir um harmônico superior apenas mediante o aumento da tensão da corda.
IV. Ondas estacionárias não são decorrentes de fenômenos de interferência e ressonância.
Assinale a alternativa correta:
a) Somente as afirmativas II e IV são verdadeiras.
b) Somente as afirmativas III e IV são verdadeiras.
c) Somente as afirmativas I e III são verdadeiras.
d) Somente as afirmativas I, III e IV são verdadeiras.
e) Somente a afirmativa II é verdadeira.
7. (Ufrgs 2016) A figura abaixo representa uma onda estacionária produzida em uma corda de
comprimento L  50cm.
Sabendo que o módulo da velocidade de propagação de ondas nessa corda é 40m s, a
frequência da onda é de
a) 40Hz.
b) 60Hz.
c) 80Hz.
d) 100Hz.
e) 120Hz.
8. (Unesp 2016) Um experimento foi feito com a finalidade de determinar a frequência de
vibração de um diapasão. Um tubo cilíndrico aberto em suas duas extremidades foi
parcialmente imerso em um recipiente com água e o diapasão vibrando foi colocado próximo
ao topo desse tubo, conforme a figura 1. O comprimento L da coluna de ar dentro do tubo foi
ajustado movendo-o verticalmente. Verificou-se que o menor valor de L, para o qual as ondas
sonoras geradas pelo diapasão são reforçadas por ressonância dentro do tubo, foi de 10 cm,
conforme a figura 2.
Considerando a velocidade de propagação do som no ar igual a 340 m s, é correto afirmar
que a frequência de vibração do diapasão, em Hz, é igual a
a) 425.
b) 850.
c) 1.360.
d) 3.400.
e) 1.700.
9. (Fac. Albert Einstein - Medicin 2016) Em 1816 o médico francês René Laënnec, durante um
exame clínico numa senhora, teve a ideia de enrolar uma folha de papel bem apertada e
colocar seu ouvido numa das extremidades, deixando a outra livre para ser encostada na
paciente. Dessa forma, não só era evitado o contato indesejado com a paciente, como os sons
se tornavam muito mais audíveis. Estava criada assim a ideia fundamental do estetoscópio [do
grego, “stêthos” (peito) “skopéo” (olhar)].
É utilizado por diversos profissionais, como médicos e enfermeiros, para auscultar (termo
técnico correspondente a escutar) sons vasculares, respiratórios ou de outra natureza em
diversas regiões do corpo.
É composto por três partes fundamentais. A peça auricular tem formato anatômico para
adaptar-se ao canal auditivo. Os tubos condutores do som a conectam à peça auscultatória.
E, por fim, a peça auscultatória, componente metálico colocado em contato com o corpo do
paciente. Essa peça é composta por uma campânula, que transmite melhor os sons de baixa
frequência - como as batidas do coração - e o diafragma, que transmite melhor os sons de alta
frequência, como os do pulmão e do abdômen.
A folha de papel enrolada pelo médico francês René Laënnec pode ser interpretada como um
tubo sonoro aberto. Considerando o comprimento desse tubo igual a 34 cm e que, ao
auscultar um paciente, houve a formação, no interior desse tubo, de uma onda estacionária
longitudinal de segundo harmônico e que se propagava com uma velocidade de 340 m / s, qual
a frequência dessa onda, em hertz?
a) 250
b) 500
c) 1000
d) 2000
10. (Efomm 2016) Um diapasão com frequência natural de 400 Hz é percutido na proximidade
da borda de uma proveta graduada, perfeitamente cilíndrica, inicialmente cheia de água, mas
que está sendo vagarosamente esvaziada por meio de uma pequena torneira na sua parte
inferior. Observa-se que o volume do som do diapasão torna-se mais alto pela primeira vez
quando a coluna de ar formada acima d’água atinge uma certa altura h. O valor de h, em
centímetros, vale
Dado: velocidade do som no ar vSom  320 m s
a) 45
b) 36
c) 28
d) 20
e) 18
11. (Ebmsp 2016)
O canal auditivo da figura representa o órgão de audição humano que mede, em média, cerca
de 2,5 cm de comprimento e que pode ser comparado a um tubo sonoro fechado, no qual a
coluna de ar oscila com ventre de deslocamento na extremidade aberta e nó de deslocamento
na extremidade fechada.
Considerando-se que a velocidade de propagação do som no ar é igual a 340 m s e que a
coluna de ar oscila segundo um padrão estacionário fundamental no canal auditivo, pode-se
afirmar – pela análise da figura associada aos conhecimentos da Física – que
a) o comprimento da onda sonora que se propaga no canal auditivo é igual a 2,5 cm.
b) a frequência das ondas sonoras que atingem a membrana timpânica é, aproximadamente,
igual a 13.600,0 Hz.
c) a frequência fundamental de oscilação da coluna de ar no canal auditivo é igual a 340,0 Hz.
d) a frequência de vibração da membrana timpânica produzida pela oscilação da coluna de ar é
igual a 3.400,0 Hz.
e) a frequência do som transmitido ao cérebro por impulsos elétricos é o dobro da frequência
da vibração da membrana timpânica.
12. (Acafe 2015) Um professor de Física, querendo ensinar ondas estacionárias aos seus
alunos, construiu um experimento com duas cordas, como mostra a figura. Pressionou a corda
1 a 80 cm do ponto fixo e, tocando na corda, criou o primeiro harmônico de uma onda
estacionária. Sabendo que a frequência conseguida na corda 1 e 440 hz, e que a velocidade
da onda na corda 2 é o dobro da velocidade da onda na corda 1, determine a posição que
alguém deverá pressionar a corda 2 para conseguir o primeiro harmônico de uma onda
estacionária com o dobro da frequência conseguida na corda 1.
A alternativa correta é:
a) C.
b) A.
c) B.
d) D.
13. (Udesc 2015) Dois tubos sonoros de mesmo comprimento se diferem pela seguinte
característica: o primeiro é aberto nas duas extremidades e o segundo é fechado em uma das
extremidades. Considerando que a temperatura ambiente seja de 20C e a velocidade do som
igual a 344 m / s, assinale a alternativa que representa a razão entre a frequência fundamental
do primeiro tubo e a do segundo tubo.
a) 2,0
b) 1,0
c) 8,0
d) 0,50
e) 0,25
14. (Enem PPL 2015) Em uma flauta, as notas musicais possuem frequências e comprimentos
de onda (λ ) muito bem definidos. As figuras mostram esquematicamente um tubo de
comprimento L, que representa de forma simplificada uma flauta, em que estão representados:
em A o primeiro harmônico de uma nota musical (comprimento de onda λ A ), em B seu
segundo harmônico (comprimento de onda λB ) e em C o seu terceiro harmônico (comprimento
de onda λ C ), onde λ A  λB  λ C .
Em função do comprimento do tubo, qual o comprimento de onda da oscilação que forma o
próximo harmônico?
L
a)
4
L
b)
5
L
c)
2
L
d)
8
6L
e)
8
15. (Uern 2015) Uma pessoa, ao soprar na extremidade aberta de um tubo fechado, obteve o
som do primeiro harmônico cuja frequência é 375Hz. Se o som no local se propaga com
velocidade de 330m / s, então o comprimento desse tubo é de
a) 20cm.
b) 22cm.
c) 24cm.
d) 26cm.
16. (Ufmg 2013) Uma corda esticada e presa nas duas extremidades pode vibrar em
diferentes frequências, sendo a mais baixa delas denominada frequência do modo
fundamental. Em um violino, a distância entre as extremidades em cada corda é de 0,32 m.
Maria Sílvia coloca esse violino próximo a um autofalante conectado a um dispositivo capaz de
produzir sons com frequências que variam continuamente entre 500 Hz e 1.500 Hz. Ela
observa que uma das cordas oscila apenas quando o dispositivo emite sons com as
frequências de 880 Hz e 1.320 Hz.
a) Na situação dessa corda vibrando em seu modo fundamental, DETERMINE:
1. a frequência da vibração.
2. o comprimento de onda da onda na corda.
b) Com relação ao som emitido por essa corda quando ela vibra em seu modo fundamental,
DETERMINE:
1. a frequência dessa onda sonora.
2. o comprimento de onda dessa onda sonora.
17. (Ufpr 2013) Um instrumento musical de cordas possui cordas metálicas de comprimento L.
Uma das cordas possui diâmetro d, densidade ρ e, quando sujeita a uma tensão T, vibra com
uma frequência fundamental de 420 Hz. Suponha que um músico troque essa corda por outra
de mesmo material e comprimento, mas com a metade do diâmetro da corda original.
Considere que as cordas estão fixas nas suas extremidades. Faça o que se pede, justificando
suas respostas.
a) Encontre a expressão para a velocidade de propagação da onda na corda em função das
grandezas T, d e ρ.
b) Determine a velocidade da onda na nova corda, quando sujeita a uma tensão quatro vezes
superior à primeira, em função da velocidade na corda original.
c) Calcule a frequência fundamental nessa nova situação.
18. (Fuvest 2013) Uma flauta andina, ou flauta de pã, é constituída por uma série de tubos de
madeira, de comprimentos diferentes, atados uns aos outros por fios vegetais. As extremidades
inferiores dos tubos são fechadas. A frequência fundamental de ressonância em tubos desse
tipo corresponde ao comprimento de onda igual a 4 vezes o comprimento do tubo. Em uma
dessas flautas, os comprimentos dos tubos correspondentes, respectivamente, às notas Mi
(660 Hz) e Lá (220 Hz) são, aproximadamente,
(Note e adote: A velocidade do som no ar é igual a 330 m/s.)
a) 6,6 cm e 2,2 cm.
b) 22 cm e 5,4 cm.
c) 12 cm e 37 cm.
d) 50 cm e 1,5 m.
e) 50 cm e 16 cm.
Gabarito:
Resposta da questão 1:
a) Comprimento de onda λ :
O comprimento de onda na corda é obtido através da contagem de cada onda completa na
figura relacionando com o comprimento total da corda.
1,20 m
λ
 λ  0,40 m
3
b) Velocidade de propagação da onda na corda:
v  λ  f  v  0,40 m  6 Hz  v  2,4 m s
Resposta da questão 2:
[D]
Sabendo que a velocidade de propagação de uma onda na corda depende da intensidade da
força de tração T na mesma e da sua densidade linear μ, de acordo com a equação:
v
T
μ
E que a onda refratada na corda de menor densidade linear possui o triplo da velocidade da
corda de maior densidade linear, podemos relacionar as duas equações lembrando que as
trações nas cordas são iguais.
Para a corda 1:
T
v1 
μ1
E para a corda 2:
T
v 2  3 v1 
μ2
Fazendo a razão da corda 2 pela 1:
3 v1

v1
T
μ2
T
μ1
3
μ1
μ2
 μ1  9 μ2
Por fim, o pulso da corda de maior densidade não sofre inversão de fase ao encontrar com a
corda menor, nem para a refração e tão pouco para a reflexão. Ver figura ilustrativa abaixo.
Resposta da questão 3:
[B]
A força tensora na corda é dada por:
T  v 2  μ (1), onde:
v  λf 
μ
2L
2  0,9 m
f 
 200 Hz  v  120 m / s
3
3
m 0,1 kg
1

 μ  kg / m
L
0,9m
9
Substituindo em (1), temos:
2 1
T  120 m / s   kg / m  T  1600 N
9
Logo, o produto da força tensora com o comprimento da corda, em N  m, será de:
T  L  1600 N  0,9 m  T  L  1440 N  m
Resposta da questão 4:
[C]
[I] Verdadeiro. Reduzindo a distância teremos uma frequência maior e um comprimento de
onda menor.
[II] Verdadeiro. Massa e comprimento de onda não são grandezas diretamente relacionadas,
entretanto, a massa e a frequência são diretamente proporcionais.
f
[III] Verdadeiro. A frequência fundamental do 4 harmônico é: f1  4  f1  150 hz, analisando
4
f5
 f1  150 hz, como ambos possuem a
a frequência fundamento do 5 harmônico: f1 
5
mesma frequência fundamental, logo a opção é verdadeira.
[IV] Falso. A velocidade transversal é diferente de velocidade da onda. Logo, teremos pontos
na corda com velocidade transversal maior ou menor que outros.
[V] Falso. A velocidade do deslocamento transversal de um ponto da corda será mínima nas
posições de cristas e vales.
Resposta da questão 5:
[A]
Violino e guitarra são instrumentos de cordas, e as ondas estacionárias em cordas, sempre
começa com um nó e termina com um nó, em todos os harmônicos. E sua amplitude nos
pontos de nó são nulas.
Resposta da questão 6:
[B]
Justificando os itens falsos:
[I] Ondas estacionárias são ondas de propagação.
[II] A Densidade da corda irá influenciar no harmônico.
Resposta da questão 7:
[E]
Para a onda estacionária em questão, tem-se:
3
2
1
L  λ  λ   0,5 m  λ  m
2
3
3
Sabendo que a velocidade da onda em função de sua frequência e de seu comprimento de
onda é dada pela equação:
v  λf
E usando a velocidade dada, obtém-se a frequência pedida.
1
v  λ  f  40 m / s  m  f  f  120 Hz
3
Resposta da questão 8:
[B]
O comprimento L corresponde a meio fuso ou a um quarto do comprimento de onda.
λ
 L  λ  4L  4  10  40 cm  λ  0,4 m.
4
Da equação fundamental da ondulatória:
v 340
v  λf  f  
 f  850 Hz.
λ 0,4
Resposta da questão 9:
[C]
A figura mostra um tubo aberto em seu segundo harmônico.
Como se pode notar nessa figura, no segundo harmônico, o comprimento de onda é igual ao
comprimento do tubo.
λ  34cm;  0,34m; v  340m/s.
Da equação fundamental da ondulatória:
v 340
v  λf  f  

f  1 000 Hz.
λ 0,34
Resposta da questão 10:
[D]
Quando o volume do som do diapasão torna-se mais alto pela primeira vez, a coluna de água
corresponde ao primeiro harmônico obtido na coluna de água.
Logo, de acordo com o desenho, a altura de líquido h é a quarta parte do comprimento da onda
sonora.
λ
h   λ  4h
4
E a expressão da velocidade da onda com a frequência e o comprimento de onda é dada por:
v
v  λ  f  v  4 hf  h 
4f
320 m / s
h
 h  0,2m  20 cm
4  400 Hz
Resposta da questão 11:
[D]
Como no primeiro harmônico há a formação de apenas uma semifusa, logo ele ocupa toda a
λ
extensão do tubo sonoro fechado, ou seja, L  . Isolando o comprimento de onda do primeiro
4
harmônico, vem:
λ
L   λ  4L  λ  4  2,5  λ  10 cm  λ  0,1m
4
v
340
V  λf  f   f 
 f  3.400 Hz
λ
0,1
Resposta da questão 12:
[C]
Analisando o enunciado, temos os seguintes dados:
 f1  440 Hz

 f2  880 Hz

 v 2  2  v1
l  80 cm  0,8 m
1
Sabendo que a frequência de um harmônico é dada por:
nv
fn 
2l
Analisando a 1ª corda, temos:
n  v1
1 v1
f1 
 440 
2  l1
2  0,8
v1  440  1,6
v1  704 m s
Agora, analisando a 2ª corda, temos:
n  v 2 n   2  v1 
1 2  704
f1 

 880 
2  l2
2  l2
2  l2
1408
880
l2  0,8 m
l2 
Resposta da questão 13:
[A]
A velocidade de uma onda expressa em função da frequência e de seu comprimento de onda
é:
v  λf
E sabendo que a velocidade de propagação de ambas são iguais:
v1  v 2  λ1  f1  λ 2  f2
λ
Para o tubo 1: L  1  λ1  2L
2
λ
Para o tubo 2: L  2  λ 2  4L
4
Com isso, a razão das frequências será:
f
λ1  f1  λ 2  f2  2L  f1  4L  f2  1  2
f2
Resposta da questão 14:
[C]
O próximo é o 4º harmônico. No caso a flauta comporta-se como um tudo aberto, sendo a
ordem do harmônico (n  4) igual a do número de fusos. Se o comprimento de um fuso é igual
ao de meio comprimento de onda, tem-se:
λ
L
4 L 
λ .
2
2
Resposta da questão 15:
[B]
Utilizando os conceitos acerca de tubos fechados e sabendo que a frequência no tubo fechado
é dada por:
v
fi  i 
4 L
Onde, i é número do harmônico.
Assim, tratando-se do primeiro harmônico, temos que:
330
f1  1
 375
4 L
330
L
4  375
L  0,22 m
Resposta da questão 16:
Dados: L = 0,32 m; vsom = 330 m/s.
a) 1. A corda somente vibra quando entrar em ressonância com a onda sonora emitida pelo
autofalante. As frequências de ressonância são múltiplas inteiras da frequência fundamental
(fn = n f1). Como temos duas ressonâncias consecutivas, temos também duas frequências
consecutivas ou dois harmônicos consecutivos (n e n + 1). Assim:
fn  880  n f1  880 I
I


fn1  1320   n  1 f1  1320 II II
n
2

 3 n  2 n  1  n  2.
n 1 3
n f1
880

n

1
f
1320
 1

Voltando em (I):
2 f1  880  f1  440 Hz.
2. O comprimento de onda correspondente à frequência é:
λ1  2 L  2 0,32  λ1  0,64 m.
b) 1. A frequência do som emitido é igual à frequência de vibração da corda.
Fsom = f1 = 440 Hz.
2. Aplicando a equação fundamental da Ondulatória:
330
v som  λ som fsom  λ som 
 λ som  0,75 m.
440
Resposta da questão 17:
a) Sendo T a força tensora, a equação de Taylor nos dá que a velocidade de propagação
das ondas numa corda é:
T
v
. I
μ
Supondo que ρ seja a densidade volumétrica da corda, sendo μ a sua densidade linear,
tiremos a relação entre as duas:

m
μ  L


4 m
m
ρ  m 


V π d2
π d2 L

L
4


μ
ρ π d2
.
4
 
μ m π d2 L


ρ L
4 m

(II)
Substituindo (II) em (I):
T
T
v
 v
μ
ρ π d2
 v
4T
ρ π d2

4
v
2 T
.
d π ρ
b) Dados: d’ = d/2 e T’ = 4 T.
Da expressão final do item anterior:

2 T
.
v 
d π ρ


v '  2 T '  v '  2 4 T  v '  2  2  2 T

d
d' π ρ
π ρ
d
π ρ

2
2 T 
 v'  4
.
 d π ρ 


v '  4 v.
c) Dado: f1 = 420 Hz.
Para o som fundamental:

v
f1  2 L


f '  v '  4 v  4  v 


1 2 L 2 L
2 L

 f1'  4 f1  4  420  
f1'  1.640 Hz.
Resposta da questão 18:
[C]
Conciliando a informação do enunciado e a equação fundamental da ondulatória:

λ
λ  4 L  L  4 (I)
v
(II) em (I): L 
.

4 f
λ  v (II)

f
Aplicando a expressão para as duas frequências pedidas:
v
330
1

 LMi 

 LMi  0,125 m 
LMi 
4 fMi
4  660 8

L  12,5 cm.
 Mi
v
330
3

 LLá 

 LLá  0,375 m 
LLá 
4
f
4

220
8

Lá
L  37,5 cm.
 Lá
