Resposta da questão

1)
Em atmosfera de ar calmo e densidade uniforme da, um balão aerostático,
inicialmente de densidade d, desce verticalmente com aceleração constante de módulo
a. A seguir, devido a uma variação de massa e de volume, o balão passa a subir
verticalmente com aceleração de mesmo módulo a. Determine a variação relativa do
volume em função da variação relativa da massa e das densidades da e d.
Resposta da questão
A figura ilustra as duas situações, descida e subida.
Desprezando o atrito com o ar, a resultante das forças sobre o balão é entre o Peso e o
Empuxo. Aplicando o Princípio Fundamental da Dinâmica às duas situações:

Descida : P1  E1  m1 a


Subida : E2  P2  m2 a
I.
II.
Isolando o volume em (I):
m1 g  da V1 g  m1 a  da V1 g  m1  g  a  
V1 
m1  g  a 
da g
III.
Ainda em (I), isolando a aceleração:
d V1 g  da V1 g  d V1 a  V1 g  d  da   V1 d a 
 d  da 
a  g

 d 
IV .
Isolando o volume em (II):
da V2 g  m2 g  m2 a  da V2 g  m2 a  g 
V2 
m2  g  a 
da g
 V .
Dividindo (V) por (III) e substituindo (IV) no resultado obtido:
V2 m2  g  a 

V1 m1  g  a 

 d  d  da
V2 m2 
d


V1 m1  d  d  da

d

V2 m2  2d 

 1 .

V1 m1  da

d  da

V2 m2  g  g d


d  da
V1 m1 
gg
d



 








  d  da  
 g 1

V2 m2  
d  


V1 m1   d  da  
g
1

 

d  
 
V2 m2  2d  da 


 
V1 m1  da 
Mas:
V2  V1  ΔV e m2  m1  Δm .
Então:
V1  V  m1  m   2 d 
V  m   2 d 

 1  1 
 1 
 1 


V1
m
d
V1 
m1   da

1
 a


V  m   2 d 
 1 
 1  1.

V1 
m1  da

2) O GPS (sigla em inglês para sistema global de posicionamento) é composto por uma
malha de 24 satélites que orbitam a Terra a uma altitude fixa e com velocidade
constante. Nesses satélites estão instalados relógios atômicos que podem aferir o tempo
com precisão de nanossegundos. Os satélites emitem ondas eletromagnéticas que se
propagam com a velocidade da luz c. Essas ondas são codificadas de modo a fornecer
as coordenadas do satélite e o instante em que o sinal foi emitido. Num certo instante t,
o receptor capta os sinais de vários satélites e, a partir dos sinais obtidos de quatro
satélites distintos, calcula as coordenadas (x, y, z) do receptor e o instante de tempo da
recepção. A figura a seguir representa uma versão unidimensional de um GPS, na qual
os satélites foram substituídos por duas antenas fixas que emitem sinais informando
suas posições e os instantes da emissão (X1, t1) e (X2, t2). Um veículo equipado com um
GPS, que se move em uma dimensão, pode ter sua localização X e o instante t
conhecidos, obtendo simultaneamente os sinais das duas antenas.
Considerando o exposto, determine as equações que fornecem a posição e o instante de
tempo do veículo (X e t) em função das coordenadas das antenas, dos instantes de
emissão e da velocidade da luz c .
Resposta da questão
Do movimento uniforme: S = vt, sendo v é a velocidade da luz: v = c. Assim:
X  ct
Para a antena 1:
X – X1 = c(t – t1)  X = X1 + c(t – t1) (equação I)
Para a antena 2:
X – X2 = -c(t = t2)  X = X2 – c(t – t2) (equação II)
Somando essas duas equações (I + II), vem:
X + X = [X1 + c(t – t1)] + [ X2 – c(t – t2)]  2X = X1 + X2 + c(t – t1 – t + t2)  X =
X1  X2  c(t 2  t1 )

2
X=
X1  X2 c
  t 2  t1  .
2
2
Subtraindo essas equações (I – II), vem
X – X = [X1 + c(t – t1)] – [X2 – c(t – t2)] 
0 = X1 – X2 + c(t – t1 + t – t2) 
0 = X1 – X2 + 2ct + c(-t1 – t2).
Da figura dada: X1 = X2 – L. Então:
0 = X2 – L – X2 + 2ct – c(t1 + t2) 
L + c(t1 + t2) = 2ct 
t=
L t1  t 2

2c
2
3) Em uma prova de atletismo, um corredor, que participa da prova de 100 m rasos,
parte do repouso, corre com aceleração constante nos primeiros 50 m e depois mantém a
velocidade constante até o final da prova. Sabendo que a prova foi completada em 10 s,
calcule o valor da aceleração, da velocidade atingida pelo atleta no final da primeira
metade da prova e dos intervalos de tempo de cada percurso.
Resposta da questão
- Cálculo da velocidade.
Dados: ΔS1  50m; ΔS2  50m.
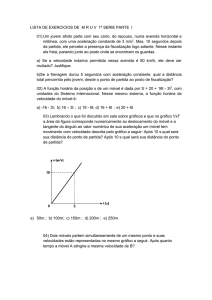
Construindo o gráfico da velocidade em função do tempo para os 10 segundos:
Sabemos que no gráfico da velocidade em função do tempo, a área entre a linha do
gráfico e o eixo dos tempos é numericamente igual ao espaço percorrido. Então:
vt
vt

 50 
 v t  100 I
ΔS1  A1 
2
2

ΔS  A  v 10  t   50  v 10  t   50  10 v  v t
2
 2
II
(I) em (II):
50  10 v  100 
v  15 m/s.
- Cálculo da aceleração.
Aplicando a equação de Torricelli no trecho acelerado:
v2  v02  2 a ΔS1  152  02  2 a 50
 225  100 a 
a  2,25 m/s2.
- Cálculo os tempos.
Voltando em (I):
v t  100  15 t  100  t 
100
20
 t
s.
15
3
Então, conforme mostra o gráfico:
Δt1  t 
Δt1 
Δt2  10  t  10 
20
s.
3
20

3
Δt2 
10
s.
3
4) Para fazer um projeto da barragem de uma usina hidrelétrica de 19,8 m de altura, o
projetista considerou um pequeno volume de água ΔV caindo do topo da barragem a
uma velocidade inicial de 2 m/s sobre as turbinas na base da barragem. Considerando o
exposto, calcule a velocidade do volume de água ΔV ao chegar à turbina na base da
barragem.
Resposta da questão
Dados: v0 = 2 m/s; h = 19,8 m; g =10 m/s2.
Desprezando a ação de forças dissipativas, podemos aplicar a conservação da energia
mecânica:
final
inicial
EMec
 EMec

m v2 m v02

 mgh
2
2
 v 2  v 02  2 g h

v2  42  2 10  9,8   v 2  400 
v  20 m/s .
5) O atleta húngaro Krisztian Pars conquistou medalha de ouro na olimpíada de Londres
no lançamento de martelo. Após girar sobre si próprio, o atleta lança a bola a 0,50m
acima do solo, com velocidade linear inicial que forma um ângulo de 45° com a
horizontal. A bola toca o solo após percorrer a distância horizontal de 80m.
Nas condições descritas do movimento parabólico da bola, considerando a aceleração da
gravidade no local igual a 10 m/s2, 2 igual a 1,4 e desprezando-se as perdas de energia
mecânica durante o voo da bola, determine, aproximadamente, o módulo da velocidade
de lançamento da bola, em m/s.
Resposta da questão
Dados: A = 80 m;
2=
1,4; g = 10 m/s2.
As componentes da velocidade inicial são:
2
vox  voy  v0 cos 45  vox  voy  v0
2
 v ox  v oy  0,7v 0 .
Desprezando a altura inicial do lançamento, a expressão do alcance horizontal (A) é:
v2
v2
A  0 sen  2θ  80  0 sen 90  v0  800  20 2  20  1,4 
g
10
v0  28 m / s.
6) Um corpo esférico, pequeno e de massa 0,1 kg, sujeito a aceleração gravitacional de
10 m/s2, é solto na borda de uma pista que tem a forma de uma depressão hemisférica,
de atrito desprezível e de raio 20 cm, conforme apresentado na figura. Na parte mais
baixa da pista, o corpo sofre uma colisão frontal com outro corpo, idêntico e em
repouso.
Considerando que a colisão relatada seja totalmente inelástica, determine o módulo da
velocidade dos corpos, em m/s, imediatamente após a colisão e a intensidade da força de
reação, em newtons, que a pista exerce sobre os corpos unidos no instante em que, após
a colisão, atingem a altura máxima.
Resposta da questão
Pela conservação da energia mecânica, calculamos a velocidade (v), antes da colisão, do
corpo esférico que é abandonado.
Dados: v0 = 0; H = R = 20 cm = 0,2 m; g = 10 m/s2.
inicial
final
EMec
 EMec
 mgR 
mv2
2
 v  2gR  2 10 0,2   v  2 m / s.
Como o choque é inelástico, pelo teorema do sistema isolado, calculamos a velocidade
(v’) do conjunto após a colisão.
depois
Qantes
 mv  2mv '  v ' 
sist  Qsist
v 2

2 2
 v '  1 m / s.
Usando novamente a conservação da energia mecânica, calculamos a altura (h) atingida
pelo conjunto formado pelos dois corpos esféricos.
inicial
final
EMec
 EMec

mv '2
v '2 12
 mgh  h 

2
2g 20
 h  0,05 m.
Nessa altura, a velocidade se anula. Então a intensidade da forma normal Fn  aplicada
pela pista tem a mesma intensidade da componente radial Pn  da força peso do
conjunto.
Na figura, as medidas estão expressas em cm.
No triângulo hachurado:
cos  
15
 0,75.
20
Fn  Pn  2mgcos   2  0,110  0,75   Fn  1,5 N.