FCM 208 Física (Arquitetura)

Universidade de São Paulo
Instituto de Física de São Carlos - IFSC
FCM 208 Física (Arquitetura)
Estática e dinâmica dos fluidos: Hidraulica
Prof. Dr. José Pedro Donoso
Termas de Pompéia
Por volta de 80 c.C., Caio
Sérgio Orata apresentou uma
idéia para cultivar ostras em
águas cálidas. Sua ideia
consistia em colocar uma série
de tanques sobre pilares de
tijolos e instalar fornalhas para
circular ar quente nos tanques.
Este mesmo princípio foi
aplicado depois para
habitações e para banhos
públicos, que os romanos
chamavam de termas.
O calor emanava de uma fornalha. Uma caldeira fornecia água para o banho,
enquanto o ar aquecido subia pelas paredes ocas e aquecia o recinto.
Coleção História em Revista: Impérios em Ascensão
Editora Cidade Cultural, 1990
Considere um tanque cheio de um líquido (de densidade ρ)
A pressão no fundo do tanque é: P = F/A = mg/A
Se A é a área do tanque e h a altura do líquido, o volume do
líquido é: V = Ah,
a pressão no fundo do tanque é: P = ρVg/A = ρgh
Como a pressão atmosférica Po também atua na superfície do líquido,
a pressão total no fundo do tanque é: P = Po + ρgh
Pressão atmosférica: Po = 1.01 × 105 N/m2 ou 101 k Pa
Densidades:
Água: ρ = 1 g/cm3 = 1000 kg/m3
Ar: 1.2×10-3 g/cm3 = 1.2 kg/m3
Equação de Continuidade
Num líquido em movimento com
velocidade v, a vazão (A•v) é constante:
A1v1 = A2v2
Aplicações: quando a água sai
da torneira, sua velocidade
aumenta enquanto a área da
seção reta diminui.
No caso da mangueira, quando
fechamos parcialmente a sua
extremidade, diminuimos a área
da seção reta, aumentando a
velocidade do líquido.
Halliday, Resnick, Walker, Fundamentals of Physics; Cutnell & Johnson, Physics
Equação de Bernoulli
matemático suizo que
calculou o trabalho
realizado por uma força
para levar um volume de
líquido até uma altura h:
P1 + 12 ρv12 + ρgh1 = P2 + 12 ρv22 + ρgh2
Aplicações
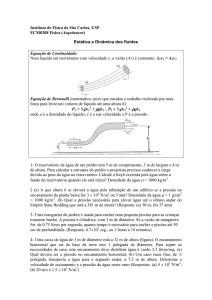
1 - Um tanque de gasolina de 2 m × 2.5 m × 2.5 m esta cheio de gasolina
(densidade ρ = 0.683 g/cm3 ou 683 Kg/m3). Encontre a pressão no fundo do tanque
e a força exercida no fundo.
Respostas: P = Po + Pgasolina = 1.18 × 105 N/m2 ou 118 k Pa; F = 5.9 × 105 N
2- (a) A que altura h se elevará a água pela tubulação de um edifício se a pressão
no encanamento da planta baixa for 3 × 105 N/m2? Densidade da água ρ = 1 g/cm3
= 1000 kg/m3.
Resposta: h = 30.6 m
2(b) Qual a pressão necessária para elevar água até o ultimo andar do Empire
State Building que está a 381 m de altura?
Resposta: P = 37 atm
3(a) - A água entra em uma casa através de
um encanamento com diámetro interno de 2
cm e com uma pressão de 4×105 Pa (cerca
de 4 atm). Um encanamento co diámetro
interno de 1 cm se liga ao banheiro do
segundo andar, a 5 m de altura. Sabendo
que no cano da entrada a velocidade é igual
a 1.5 m/s, ache (a) a velocidade do
escoamento, (b) a pressão e (c) a vazão
volumétrica no banheiro.
Respostas:
(a) 6 m/s (b) 3.3×105 Pa (c) 0.47 litros/seg
Ref: Sears & Zemansky, Física II (10a ed)
3(b) - A água que circula numa residência vem do encanamento no solo. A água
entra na casa através de um cano de 8 cm de diámetro com velocidade v = 0.6 m/s
e pressão de 4 × 105 N/m2. (a) Qual a velocidade da água num cano de 5 cm de
diámetro no 3o andar, a 9 m de altura? (b) Qual a pressão da água no 3o andar?
Respostas: (a) 1.5 m/s, (b) 3.1 × 105 N/m2 = 311 k Pa
4- Uma caixa de água de 3 m de
diámetro está a 32 m de altura. O
encanamento horizontal que sai da base
da torre tem 1 polegada de diámetro.
Para suprir as necessidades de casa,
este encanamento deve distribuir água à
vazão de 2.5 litros/s ou seja, 0.0025 m3/s.
(a) Qual devera ser a pressão no encanamento horizontal
(b) Um cano mais fino, de ½ polegada, transporta a água para o segundo andar,
a 7.2 m de altura. Determine a velocidade de escoamento e a pressão da
água neste cano
Respostas: (a) 4 × 105 N/m2; (b) 20 m/s e 1.5 × 105 N/m2
Halliday, Resnick, Krane, Física, Exemplo 18-2 (Editora LTC)
Aplicações da Eq. de Bernoulli
A forma da asa de avião (aerofólio) tem uma
curvatura maior na parte de cima. Quando o
avião começa a correr na pista, a velocidade do
ar na parte de cima da asa é maior do que na
parte de baixo. De acordo com a Eq. de
Bernouilli, isto significa que a pressão no lado de
cima da asa é menor que a pressão do lado de
baixo da asa e, portanto, existe uma força para
cima, chamada força de sustentação F
(
)
F = ∆P ⋅ A = 12 ρ v22 − v12 ⋅ A
Sears & Zemansky
Física II (10a ed)
Trefil & Hazen
Física Viva, vol. 1
Um esquiador inclina o corpo para a frente
durante um salto para produzir uma força
de sustentação que ajuda a aumentar a
distância percorrida
A lona que cobre a carga do caminhão está
plana (flat) quando o veículo está parado, mais ela
se encurva para cima quando o veículo está em
movimento. A força do vento cria uma diferença
de pressão entre o lado de baixo e o lado de cima
da lona.
J.D. Cutnell & K.W. Johnson
Physics (3rd ed., 1995)
O cano de saída de uma pia possui
um sifão (water trap) que retém um
pouco de água, evitando assim que
o mau cheiro do esgoto (sewer)
chegue ao ralo.
De acordo com o princípio de
Bernouilli, a passagem de água no
cano principal do esgoto faz a
pressão diminuir, o que poderia
remoner a água do sifão. Para evitar
que isto aconteça, o encanamento
dispõe de um suspiro (vent) que
iguala as pressões dos dois lados do
sifão.
Trefil & Hazen. Física Viva
Cutnell & Johnson, Physics
Ar em movimento: ventos
Os ventos em uma cidade podem tomar caminhos
inesperados. Um edifício representa um obstáculo
forçando o vento a se desviar para os lados e por cima,
dividindo-se em correntes de ar descendentes e
obliquas.
Os ventos defletidos por edifícios vizinhos podem
convergir em rajadas. Na cidade de Chicago, há certos
trechos da Michigan Av. com corrimões para os
pedestres se asegurarem quando sopram ventos fortes.
Um vento de 65 km/h pode impedir uma pessoa normal
de caminhar, e uma turbulência de 16 km/h pode
derrubar uma pessoa.
E. Hecht, Physics
(Brooks Cole Publ. 1994)
Coleção Ciência & Natureza
Tempo e Clima
Time – Life e Ed Abril, 1995
Ao soprar em um edifício alto, o vento se divide em várias correntes de ar. Parte do
ar desce pela face do edifício, chega à calçada e se converte em contracorrente.
Ele vai também pela esquerda e pala direita, envolvendo o edifício e avançando
para baixo, em direção à rua. O ar que bate nas laterais do edifício se torna uma
corrente veloz. Os ventos defletidos por altos edifícios vizinhos podem se fundir e
gerar fortes ventos de vale e de rua.
Os arquitetos podem testar os efeitos de um
edifício alto sobre os ventos com uma maquete
em um tunel de vento. A fumaça mostra as
correntes de ar.
Os edifícios altos criam turbulências ao alterar a
rota dos ventos estáveis de superfície. Eles
obrigam o ar a se elevar, no processo
conhecido como ascensão orográfica. Na foto,
várias linhas de fumaça mostram os padrões de
fluxo atmosférico em torno de maquetes de um
edifício pequeno (em cima) e de um edifício alto
(embaixo). Nos dois casos, parte do vento que
chega ao edifício é defletida para o alto
formando torvelinhos e redemoinhos.
B. Walpole, Ciência Divertida: Ar (Melhoramentos, 1991)
Tempestade (furacão). A pressão no
exterior caiú bruscamente, ficando muito
menor que a pressão interna na
residência. A diferença das pressões
arrancou o telhado. Se os ocupantes
tiverem deixado várias janelas abertas,
de forma a igualar as pressões, isso não
teria ocorrido.
E. Hecht, Physics (Brooks & Cole, 1994)
5 -Quando o vento sopra forte sobre um telhado,
a diferença entre a pressão atmosférica Po no
interior de uma casa e a pressão reduzida sobre
o telhado pode arrancar o telhado. Imagine que
um vento de 100 km/h sopre sobre um telhado
de 15 m × 15 m. Qual a diferença de pressão
entre o interior e o exterior da casa que tende a
arrancar o teto? Qual o módulo da força devida
a esta diferença de pressão sobre ele? Compare
esta força com o peso do telhado.
Resposta: F = ½ ρv2 = 1.14 × 105 N
6 – As janelas de um edifício medem 4.3 × 5.2 m. Num dia de tempestade o vento
esta soprando a 100 km/h paralelamente a uma janela do 30o andar. Calcule a
força resultante sobre a janela.
Resposta: aprox. 104 N (equivalente ao peso de 1 tonelada !)
P. Tipler, Física, Volume 1
Resnick – Halliday – Krane, Física 2
Energia cinética de uma coluna de vento:
E = 12 mv 2 = 12 ρVv 2 = ( 12 ρv 2 )V
Fluxo de ar através da coluna:
 Volume  A∆x
∆x
 =
Fluxo = 
=A
= Av
tempo
∆
t
∆
t


A taxa com que a energia é transferida
fornece a potência P:
R.A. Serway, J.W. Jewett,
Princípios de Física (Thomson, 2004)
 Energia  Volume 
 =
P=

 Volume  tempo 
(
1
2
ρv 2 )( Av ) = 12 ρv 3 A
Aplicação
Qual a potência fornecida por um gerador
eólico se a velocidade do vento for 10 m/s. O
comprimento das pás é R = 40 m. Considere
uma eficiência de 17%
Solução:
Área do catavento : A = πR2 = 5×103 m2
Potência:
(
)
P = 12 ρAv 3 = 12 (1.2) 5 ×103 (10) = 3MW
3
Potência disponivel: 0.17(3) ≈ 0.5 MW
Potência gerada por outras fontes de energia:
Uma usina Termoelétrica gera 150 MW. Seriam necessárias 300 geradores
eólicos para competir com a potência gerada por uma Termoelétrica. Um reator
nuclear gera 1 GW e uma tonelada de carvão gera apenas 170 kW.
R.A. Serway, J.W. Jewett, Princípios de Física (Thomson, 2004)