¢ ¡¤ £¦¥¨§ ©¦§

6ROXomR&RPHQWDGD3URYDGH0DWHPiWLFD
TXHVW}HV
O valor da soma 1 +
A)
B)
C)
D)
E)
1 1 1
+ + é:
2 3 6
5
4
3
2
1
4XHVWmRDOWHUQDWLYD'
Esta questão exige do candidato o conhecimento de soma de frações com denominadores diferentes.
1+
1 1 1 6 3 2 1 6 + 3 + 2 + 1 12
+ + = + + + =
=
=2
2 3 6 6 6 6 6
6
6
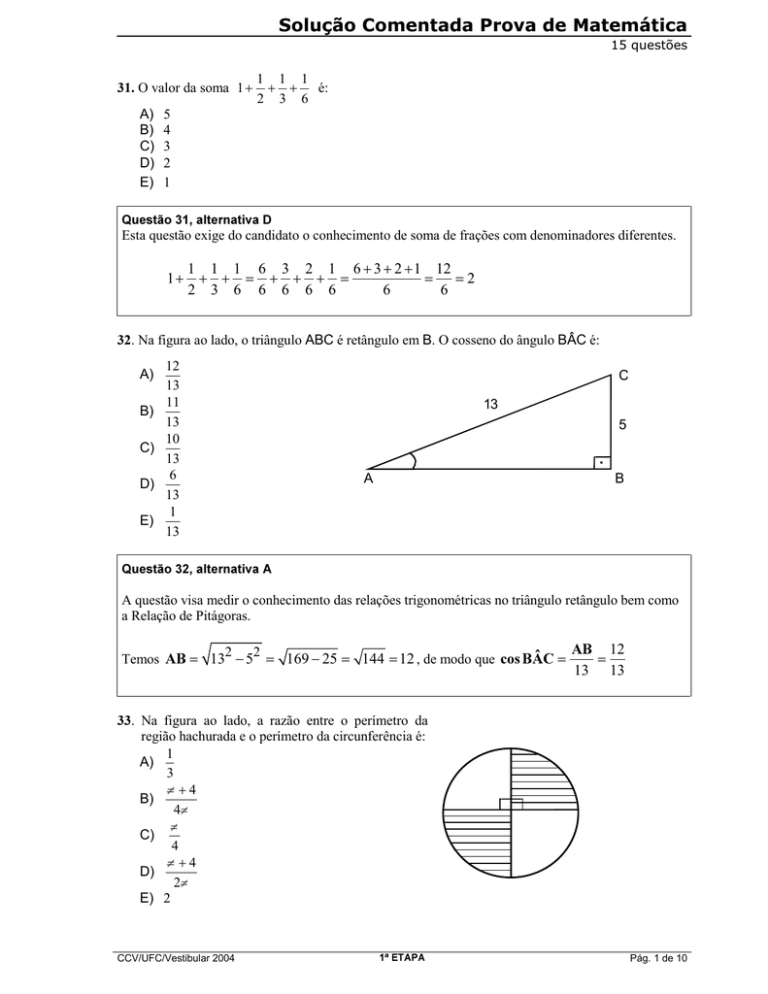
. Na figura ao lado, o triângulo ABC é retângulo em B. O cosseno do ângulo BÂC é:
A)
B)
C)
D)
E)
12
13
11
13
10
13
6
13
1
13
C
13
5
A
B
4XHVWmRDOWHUQDWLYD$
A questão visa medir o conhecimento das relações trigonométricas no triângulo retângulo bem como
a Relação de Pitágoras.
$% 12
Temos $% = 132 − 52 = 169 − 25 = 144 = 12 , de modo que FRV %Æ& =
=
13
13
. Na figura ao lado, a razão entre o perímetro da
região hachurada e o perímetro da circunferência é:
1
A)
3
π +4
B)
4π
π
C)
4
π +4
D)
2π
E) 2
CCV/UFC/Vestibular 2004
Pág. 1 de 10
6ROXomR&RPHQWDGD3URYDGH0DWHPiWLFD
TXHVW}HV
4XHVWmRDOWHUQDWLYD'
Exige do candidato o conhecimento do conceito de perímetro de uma figura e de perímetro de uma
circunferência em função do raio.
O perímetro da região hachurada é 45 + π5 e o perímetro da circunferência é
2π5 , onde R é o raio da circunferência. Logo a razão é
45 + π5 4 + π π + 4
=
=
.
2π
2π5
2π
. Numa sala há 100 pessoas, das quais 97 são homens. Para que os homens representem 96% das
pessoas contidas na sala, deverá sair que número de homens?
A)
B)
C)
D)
E)
2
5
10
15
25
4XHVWmRDOWHUQDWLYD(
Requer do candidato a noção de percentagem bem como a habilidade em traduzir as informações em
equações matemáticas.
Se x homens saem da sala, restam 100 – x pessoas, das quais 97 – x são homens. Então, 97 − [
equivale a 96% de 100 − [ . Logo, 97 − [ =
se conclui que 100 = 4[ ou x = 25.
. O valor exato de
A)
B)
C)
D)
E)
96
100 − [ ou 9700 − 100[ = 9600 − 96[ , donde
100
32 + 10 7 + 32 − 10 7 é:
12
11
10
9
8
CCV/UFC/Vestibular 2004
Pág. 2 de 10
6ROXomR&RPHQWDGD3URYDGH0DWHPiWLFD
TXHVW}HV
4XHVWmRDOWHUQDWLYD&
Visa medir a habilidade do candidato em manipular expressões numéricas envolvendo radicais e o
conhecimento de produtos notáveis fundamentais.
6ROXomR: Pondo x =
[2 =
(
32 + 10 7 + 32 − 10 7 , temos x > 0 e
32 + 10 7 + 32 − 10 7
)
2
[ 2 = 32 + 10 7 + 2 32 + 10 7 32 − 10 7 + 32 − 10 7
[ 2 = 64 + 2 1024 − 700
[ 2 = 64 + 2 324 = 100
Como x é positivo, então, x = 10.
6ROXomR: Observando que 32 = 52 + 7 , então,
(
32 + 10 7 = 52 + 25 7 + 7 = 5 + 7
(
Analogamente, 32 − 10 7 = 5 − 7
Portanto,
)
)
2
2
.
32 + 10 7 + 32 − 10 7 = 5 + 7 + 5 − 7 = 10 .
π
FRV θ + LVHQ θ
. Sabendo que L 2 = −1 e que 0 < θ < , o número complexo
é igual a:
FRV θ − LVHQ θ
2
A) FRV 2 θ + LVHQ 2 θ 1+ L
1−L
θ
θ
C) FRV   + LVHQ  
2
2
1−L
D)
1+ L
E) FRV θ 2 + LVHQ θ 2 B)
4XHVWmRDOWHUQDWLYD$
Requer do candidato o conhecimento de noções básicas sobre números complexos: conjugado de um
número complexo, relação de Euler.
Temos
FRV θ + LVHQ θ HLθ
HLθHLθ HL 2θ
=
=
=
= HL 2θ = FRV 2θ + LVHQ 2θ
−
θ
−
θ
θ
L
L
L
FRV θ − LVHQ θ H
1
H H
CCV/UFC/Vestibular 2004
Pág. 3 de 10
6ROXomR&RPHQWDGD3URYDGH0DWHPiWLFD
TXHVW}HV
. Considere a reta U cuja equação é \ = 3[ . Se 3R é o ponto de U mais próximo do ponto 4 3 3
e G é a distância de 3R a 4 , então G 10 é igual a:
A)
B)
C)
D)
E)
3
4
5
6
7
4XHVWmRDOWHUQDWLYD'
Noções básicas de geometria analítica plana: equação de uma reta, fórmula da distância de um ponto
a uma reta.
A distância de um ponto Q(m, n) à reta ax + by + c = 0) é dada pela fórmula:
G=
G=
DP + EQ + F
D2 + E 2
33 − 3
32 + −12
. O valor da soma ORJ 10
. Aplicada ao ponto Q(3, 3) e à reta 3x – y = 0, obtemos:
=
6
. Portanto G 10 = 6
10
1
2
3
99
+ ORJ 10 + ORJ 10 + + ORJ 10
é:
2
3
4
100
A) 0
B) –1
C) –2
D) 2
E) 3
4XHVWmRDOWHUQDWLYD&
Requer do candidato o conhecimento de noções básicas sobre logaritmos e suas propriedades.
Temos:
6 = ORJ10
1
2
99
+ ORJ10 + + ORJ10
2
3
100
98 99 
1 2 3
= ORJ10  ⋅ ⋅ ⋅ ⋅ ⋅
99 100 
2 3 4
1
= ORJ10
= ORJ10 10 − 2 = −2
100
CCV/UFC/Vestibular 2004
Pág. 4 de 10
6ROXomR&RPHQWDGD3URYDGH0DWHPiWLFD
TXHVW}HV
. Um poliedro convexo só tem faces triangulares e quadrangulares. Se ele tem 20 arestas e 10
vértices, então, o número de faces triangulares é:
A)
B)
C)
D)
E)
12
11
10
9
8
4XHVWmRDOWHUQDWLYD(
A Fórmula de Euler para Poliedros Convexos afirma que V + F = A + 2, onde V é o número de
vértices, F é o número de faces e A é o número de arestas. Como A = 20,
V = 10, então, F = 12. O poliedro tem 12 faces.
Se T é o número de faces triangulares e Q é o número de faces quadrangulares, então,
7 + 4= 12 e A =
37 + 44
, pois cada face triangular contribui com 3 arestas, e cada
2
face quadrangular contribui com 4 arestas e cada aresta é comum a duas faces.
Portanto, temos o sistema de equações:
7 + 4 = 12
cuja solução é 7 = 8 e 4 = 4

37 + 44 = 40
. A soma dos inteiros que satisfazem a desigualdade [ − 7 > [ + 2 + [ − 2 é:
A)
B)
C)
D)
E)
14
0
–2
–15
–18
CCV/UFC/Vestibular 2004
Pág. 5 de 10
6ROXomR&RPHQWDGD3URYDGH0DWHPiWLFD
TXHVW}HV
4XHVWmRDOWHUQDWLYD(
Requer habilidade no trato com desigualdades, função módulo e apreciação de casos.
Consideremos os seguintes casos:
Caso I: x < -2; Caso II: -2 ≤ x < 2; Caso III: 2 ≤ x < 7; Caso IV: 7 ≤ x
No &DVR,
[−7 > [+2 + [−2
−[ + 7 > −[ − 2 − [ + 2
7 > −[
−7 < [
Logo - 7 < x < -2, de modo que as soluções inteiras são -6, -5, -4, -3.
No &DVR,,
[−7 > [+2 + [−2
−[ + 7 > [ + 2 − [ + 2
3>[
A soluções inteiras são -2, -1, 0, 1.
No &DVR,,,
[−7 > [+2 + [−2
−[ + 7 > [ + 2 + [ − 2
7 > 3[
[ < 73
A solução inteira é 2.
No &DVR,9
[−7 > [+2 + [−2
[−7 > [+2+[−2
−7 > [
Não há soluções nesse caso.
A soma de todas as soluções inteiras é −6 − 5 − 4 − 3 − 2 − 1 + 0 + 1 + 2 = −18
. Na figura ao lado, cada quadradinho da
malha tem lado 1. A área do quadrilátero
ABCD é:
A) 18
B) 19
C) 20
D) 21
E) 22
C
B
A
D
CCV/UFC/Vestibular 2004
Pág. 6 de 10
6ROXomR&RPHQWDGD3URYDGH0DWHPiWLFD
TXHVW}HV
4XHVWmRDOWHUQDWLYD$
Área de retângulos e triângulos.
C
Na figura abaixo, considere os•Rpontos adicionais
P, Q, R, S e T. Tem-se:
$%&' = 34%7 + 75&6 − $4% − %5& − &6' − $'3
= 3Q
4•+ 64 −
A
14 3B4 16 27
−
−
−
= 12 + 24 − 2 − 6 − 3 − 7 = 36 − 18 = 18
2
2
2
2
•P
•T
D
•
S
 2 1   1 −1   1 0 

=
 seja verdadeira é:
 1 1   −1 D   0 1 
. O valor de D para que a igualdade matricial 
A)
B)
C)
D)
E)
1
2
0
–2
–1
4XHVWmRDOWHUQDWLYD%
Questão que exige apenas o conhecimento das operações básicas com matrizes.
1 0   2 1  1 −1 1 −2 + D 
=

=
.
0 1  1 1  −1 D  0 −1 + D 
Temos 
Por igualdade de matrizes, obtém-se:
−2 + D = 0 , donde segue que D = 2 .
CCV/UFC/Vestibular 2004
Pág. 7 de 10
6ROXomR&RPHQWDGD3URYDGH0DWHPiWLFD
TXHVW}HV
. O número máximo de pontos de interseção entre 10 circunferências distintas é:
A)
B)
C)
D)
E)
100
90
45
32
20
4XHVWmRDOWHUQDWLYD%
Conceitos básicos de contagem.
Duas circunferências distintas se cortam em, no máximo, dois pontos distintos.
Portanto, o número máximo de pontos de interseção de 10 circunferências distintas é:
10 
109
2&10 2 = 2   = 2
= 90
2
2
F[
, definida para todo número real [ tal que G[ + 3 ≠ 0 , onde F e
G[ + 3
3
G são constantes reais. Sabendo que I I [ = [ e I 5 3 = I I I I I 3 = − , podemos
5
2
2
afirmar que F + G é igual a:
. Considere a função I [ =
A)
B)
C)
D)
E)
5
25
61
113
181
CCV/UFC/Vestibular 2004
Pág. 8 de 10
6ROXomR&RPHQWDGD3URYDGH0DWHPiWLFD
TXHVW}HV
4XHVWmRDOWHUQDWLYD%
Conceitos básicos sobre funções reais de uma variável real: domínio, conjuntos de valores,
composição.
 F[ 
F

2
G[ + 3
 G[ + 3  = [ ou F [ Da condição I I [ = [ , obtemos
=[ ⇒
G[ + 3 GF[ + 3G[ + 9
 F[ 
G
+3
 G[ + 3 
F 2 = GF + 3[ + 9
Como a última igualdade é válida para todo x tal que dx + 3 ≠ 0, temos d(c+3) = 0 e
F 2 = 9. Temos as possibilidades: (I) d = 0 e c = 3 ou (II) c = -3 e d qualquer.
A segunda condição do problema é I 5 3 = − . Como I 2 [ = [ , temos que
3
5
3
I 5 [ = I [ , de modo que I 3 = − . Se fosse d = 0 e c = 3, teríamos I [ = [ e
5
3
− 3 3 − 3
I 3 = − não ocorreria. Logo, dever ser c = - 3. Das igualdades I 3 =
=
5
3G + 3 5
segue que d = 4. Portanto, F 2 + G 2 = −32 + 42 = 25 .
2875$62/8d­2: Da igualdade I I 3 = 3 obtemos I 5 3 = I 3 =
3F
3
=− .
3G + 3
5
(I)
De I 3 = − , obtemos I  −  = I I 3 = 3 . Logo,
 3
 5
3
5
3
− F
5
=3
(II)
3
− G+3
5
15F + 9G = −9
cuja solução F = −3 e G = 4 .
De (I) e (II), obtemos o sistema de equações 
− 3F + 9G = 45
Portanto, F 2 + G 2 = −3 2 + 4 2 = 25
. Se a expressão
2[ + 5
4[ 2 − 1
=
D
E
+
ondeD e E são constantes, é verdadeira paratodo
2[ + 1 2 [ − 1
número real [ ≠ ±1 2 , então o valor de D + E é:
A) –2
B) –1
C) 1
D) 2
E) 3
CCV/UFC/Vestibular 2004
Pág. 9 de 10
6ROXomR&RPHQWDGD3URYDGH0DWHPiWLFD
TXHVW}HV
4XHVWmRDOWHUQDWLYD&
Requer conhecimento de fatoração de expressões algébricas.
Temos
D
E
D 2[ − 1 + E 2[ + 1 2D + E[ + E − D
+
=
=
.
2[ + 1 2[ − 1
2[ + 1 2[ − 1
4[ 2 − 1
Portanto,
2[ + 5
4[ 2 − 1
=
2D + E[ + E − D
4[ 2 − 1
, expressão que é válida para todo x ≠ ±1/2.
Logo, 2[ + 5 = 2D + E[ + E − D , para todo x ≠ ±1/2, donde concluímos que D + E = 1 .
CCV/UFC/Vestibular 2004
Pág. 10 de 10