Exame1a

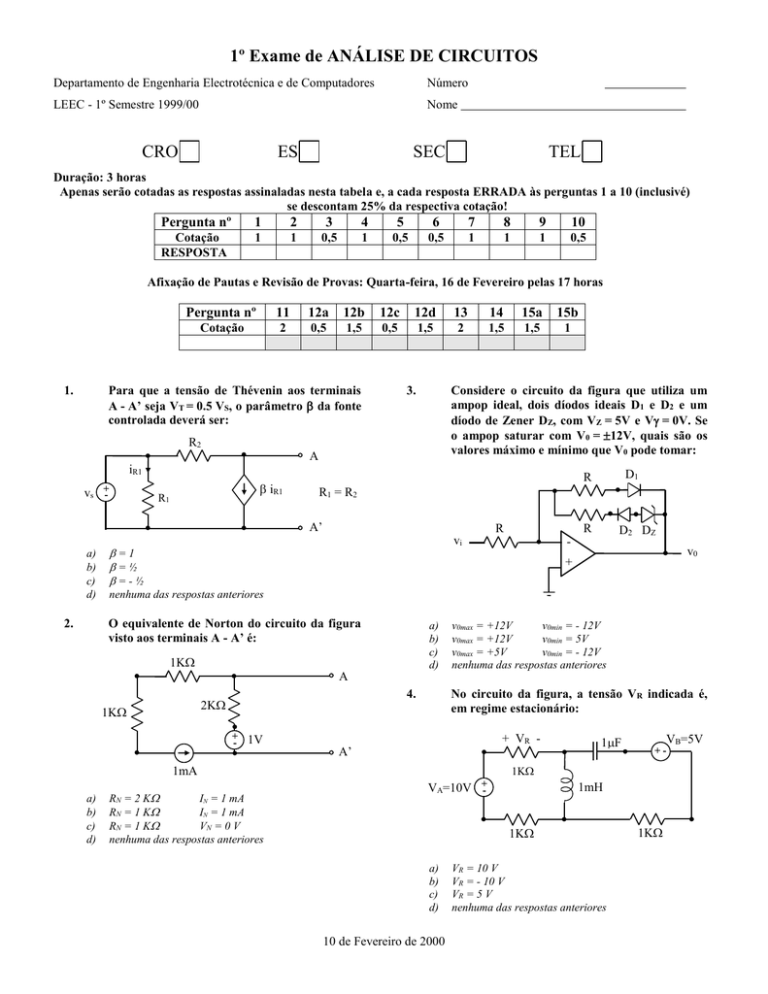
1º Exame de ANÁLISE DE CIRCUITOS
Departamento de Engenharia Electrotécnica e de Computadores
Número
LEEC - 1º Semestre 1999/00
Nome
CRO
ES
SEC
TEL
Duração: 3 horas
Apenas serão cotadas as respostas assinaladas nesta tabela e, a cada resposta ERRADA às perguntas 1 a 10 (inclusivé)
se descontam 25% da respectiva cotação!
Pergunta nº
1
2
3
4
5
6
7
8
9
10
Cotação
RESPOSTA
1
1
0,5
1
0,5
0,5
1
1
1
0,5
Afixação de Pautas e Revisão de Provas: Quarta-feira, 16 de Fevereiro pelas 17 horas
1.
Pergunta nº
11
12a
12b
12c
12d
13
14
15a
15b
Cotação
2
0,5
1,5
0,5
1,5
2
1,5
1,5
1
Para que a tensão de Thévenin aos terminais
A - A’ seja VT = 0.5 VS, o parâmetro  da fonte
controlada deverá ser:
3.
Considere o circuito da figura que utiliza um
ampop ideal, dois díodos ideais D1 e D2 e um
díodo de Zener DZ, com VZ = 5V e V = 0V. Se
o ampop saturar com V0 = 12V, quais são os
valores máximo e mínimo que V0 pode tomar:
R2
A
iR1
vs +-
 iR1
R1
A’
a)
b)
c)
d)
2.
D1
R
R1 = R2
R
R
vi
=1
=½
=-½
D2 DZ
-
v0
+
nenhuma das respostas anteriores
O equivalente de Norton do circuito da figura
visto aos terminais A - A’ é:
a)
b)
c)
d)
1K
v0max = +12V
v0min = - 12V
v0max = +12V
v0min = 5V
v0max = +5V
v0min = - 12V
nenhuma das respostas anteriores
A
4.
No circuito da figura, a tensão VR indicada é,
em regime estacionário:
2K
1K
+
-
1V
+ VR -
A’
1mA
a)
b)
c)
d)
RN = 2 K
IN = 1 mA
RN = 1 K
IN = 1 mA
RN = 1 K
VN = 0 V
nenhuma das respostas anteriores
1F
VB=5V
+-
1K
VA=10V +-
1mH
1K
a)
b)
c)
d)
10 de Fevereiro de 2000
VR = 10 V
VR = - 10 V
VR = 5 V
nenhuma das respostas anteriores
1K
1º Exame de ANÁLISE DE CIRCUITOS
5.
Considere um circuito caracterizado pelo
modelo de estados seguinte
Error! x (t) = Error! x(t) + Error! u(t)
Quando u(t) = 1V, t > 0, a solução particular
do circuito é xp(t):
a)
b)
c)
d)
6.
[½
0] T
[1
½] T
[0
½] T
nenhuma das respostas anteriores
No circuito da pergunta anterior a componente
homogénea da solução é (k1 e k2 são vectores
determinados a partir do circuito):
a)
b)
c)
d)
7.
t
-t
xh (t) = k1 e + k2 e
-t
xh (t) = (k1 + k2) e
-t
-2t
xh (t) = k1 e + k2 e
nenhuma das respostas anteriores
a)
H(s) = Error!
b)
H(s) = Error!
c)
H(s) = Error!
d)
nenhuma das respostas anteriores
10.
Para o circuito da figura, considerando a sua
resposta na frequência, trata-se de um filtro:
L
Pretendendo-se que o sinal de saída v0(t) esteja
desfasado do sinal de entrada vs(t) de /4, o
valor de C necessário é de:
R
vi
C
+
vS= cos (103t)
a)
b)
c)
d)
8.
+
-
v0(t)
R=1K
a)
b)
c)
d)
C = 10 F
C = 1 mC
C = 1 F
nenhuma das respostas anteriores
O diagrama de pólos-zeros da figura pode
corresponder a que função de transferência:
In
1
-5
-1
4
Re
-1
a)
b)
c)
d)
9.
H(s) = Error!
H(s) = Error!
H(s) = Error!
nenhuma das respostas anteriores
O diagrama de Bode de amplitude da figura
corresponde a que função de transferência:
|H|db
10 de Fevereiro de 2000
60
40
Passa-Banda
Passa-Baixo
Passa-Alto
nenhuma das respostas anteriores
v0
1º Exame de ANÁLISE DE CIRCUITOS
11.
Utilizando o método do nós, escreva na forma
matricial as equações de equilíbrio do circuito.
Respeite as convenções da figura.
13.
Considere o circuito seguinte
2R
2R
u2
R
R
+
VA +-
2R
R2
2R
2R
v0
R3
IA
u3
u1
+
 IB
+
vC -
u5
-+
Usando o Teorema da Sobreposição, determine v0 em
função de vA, vB e vC
Sugestão: Comece por determinar a contribuição de vC.
R5
R4
14.
12.
vB -
VB
u4
R1
+
vA -
Considere o circuito da figura
C1
Sabendo que a tensão vs(t) é a representada na
figura
(Tente simplificar o circuito antes de começar a
análise; admita que os condensadores estão
inicialmente descarregados)
+
R3
vs
R1
R2
C2
-
vs(t)
1V
Determine a função de transferência v0(s)/vs(s) do
circuito
t
T=1s
15.
R1=2.5K
+
-
vs(t)
v1(t)
100F=C1
F
400F=C2
F
R2=4K
+
R3
6K v0(t)
-
C3=20F
F
a)
Determine o valor de v1(0+)
b)
Calcule e esboce v1(t) e v0(t) no intervalo [0, T]
c)
Determine os valores de v1(T) e v0(T)
d)
Calcule e esboce v(t) e v0(t) no intervalo [T, +[
Sendo H(s) = Error!
a)
Represente os diagramas de Bode do ganho e fase reais
e assimptóticos de H(s).
b)
Se H(s) representar um ganho de tensão, determine a
tensão de saída v0(t) para uma entrada
vs(t)=5 cos ( t) e  =10 rad s-1
10 de Fevereiro de 2000
v0