Exame2a

2º Exame de ANÁLISE DE CIRCUITOS
Departamento de Engenharia Electrotécnica e de Computadores
Número
LEEC - 1º Semestre 1999/00
Nome
CRO
ES
SEC
TEL
Duração: 3 horas
Apenas serão cotadas as respostas assinaladas nesta tabela e, a cada resposta ERRADA às perguntas 1 a 10 (inclusivé)
se descontam 25% da respectiva cotação!
Pergunta nº
1
2
3
4
5
6
7
8
9
10
Cotação
RESPOSTA
1
1,5
1
1
0,5
1
0,5
1
1
1,5
Afixação de Pautas e Revisão de Provas: Quinta-feira, 2 de Março pelas 17H30
1.
Pergunta nº
11
12
13
14a
14b
14c
15a
15b
Cotação
2,5
1,5
2
0,5
1
1
1
0,5
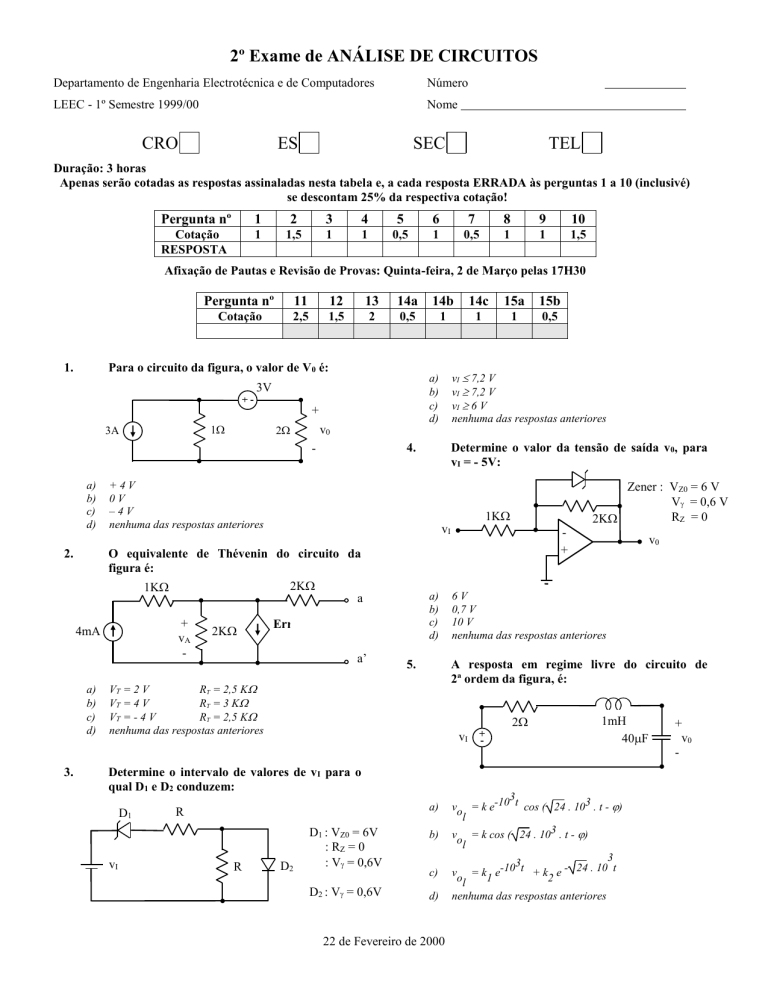
Para o circuito da figura, o valor de V0 é:
+-
+
1
3A
v0
2
4.
a)
b)
c)
d)
2.
+
vA
-
3.
2K
1K
a)
b)
c)
d)
Error!
a’
5.
2
D2
1mH
40F
a)
3
vo = k e-10 t cos ( 24 . 103 . t - )
l
D1 : VZ0 = 6V
: RZ = 0
: V = 0,6V
b)
vo = k cos ( 24 . 103 . t - )
l
c)
D2 : V = 0,6V
3
3
vo = k1 e-10 t + k2 e - 24 . 10 t
l
d)
nenhuma das respostas anteriores
R
R
v0
6V
0,7 V
10 V
nenhuma das respostas anteriores
vI +-
Determine o intervalo de valores de vI para o
qual D1 e D2 conduzem:
vI
+
A resposta em regime livre do circuito de
2ª ordem da figura, é:
VT = 2 V
RT = 2,5 K
VT = 4 V
RT = 3 K
VT = - 4 V
RT = 2,5 K
nenhuma das respostas anteriores
D1
Zener : VZ0 = 6 V
V = 0,6 V
RZ = 0
2K
vI
O equivalente de Thévenin do circuito da
figura é:
2K
1K
a
a)
b)
c)
d)
Determine o valor da tensão de saída v0, para
vI = - 5V:
+4V
0V
–4V
nenhuma das respostas anteriores
4mA
vI  7,2 V
vI  7,2 V
vI  6 V
nenhuma das respostas anteriores
a)
b)
c)
d)
3V
22 de Fevereiro de 2000
+
v0
-
2º Exame de ANÁLISE DE CIRCUITOS
6.
As equações de estado para um dado sistema
de 2ª ordem são
9.
O circuito da figura comporta-se como um
filtro:
Error!= Error! x + Error! u
y = [5
vI
+
-
0] x + 1 . u
v0
Calcule a saída y, para uma entrada u=10:
a)
b)
c)
d)
7.
L
23,5
235
470
nenhuma das respostas anteriores
Determine as potências activa e reactiva em RL
para o circuito da figura:
a)
b)
c)
d)
1
3
6 cos (10 t)V
+
-
100F
1
10mH
8.
Determine
uma
possível
função
de
transferência H(s) a que corresponde o seguinte
diagrama de amplitude de Bode:
4,5 W ; 0 VA
9 W ; 0,2 VA
4,5 W ; 0,2 VA
nenhuma das respostas anteriores
|H|dB
Supondo o circuito da figura inicialmente
(t=0-) estabilizado, calcule os valores da tensão
de saída, v0, em t=0+ e t=:
1
vI
+
-
20
0
2
vI
6V
+
v0
-
a)
b)
c)
d)
10
102
a)
H(s) = Error!
b)
H(s) = Error!
c)
H(s) = Error!
d)
nenhuma das respostas anteriores
3V
0
1
-20
0,1F
1H
Passa-Baixo
Passa-Alto
Passa-Banda
nenhuma das respostas anteriores
RL
10.
a)
b)
c)
d)
99R
R
t
v0(0+) = 1 V ; v0() = 0 V
v0(0+) = 2 V ; v0() = 0 V
v0(0+) = 0 V ; v0() = 2 V
nenhuma das respostas anteriores
22 de Fevereiro de 2000
103
104

2º Exame de ANÁLISE DE CIRCUITOS
11.
Escreva, sob forma matricial, as equações do
circuito derivadas do método nodal. Respeite
as convenções do enunciado.
VI
C
u4
u2
vI
 vA
G4
I1
+
-
+
v0
A função de transferência H(s) = Error!
b)
O respectivo diagrama de amplitude de Bode
c)
O ganho de tensão para  = 0;  = 1 krad/s;
 = 10 krad/s e  = 
Sendo H(s) = Error!
Em relação ao circuito da figura, determine as
tensões vX e u2, utilizando o teorema da
sobreposição
a)
Construa um circuito, utilizando 2 AMPOP’s, que
sintetize a função de transferência indicada.
u2
b)
Calcule o ganho do circuito para as frequências
 = 2 rad/s e  = 20 rad/s.
R1
R2
iX
+ vX  iX
E +-
I
Para o circuito da figura, determine as
condições iniciais, iL(0+), vC (0+) e iR2(0+), e as
condições finais para as mesmas grandezas,
iL(), vC(), iR2()
t=0
10V +-
R1 = 1 k
R2 = 100 k
C = 1 F
a)
15.
13.
R2
iB
G2
u3
12.
R1
G3
G1
+
-
Para o circuito da figura, calcule:
 iB
+ vA -
u1
14.
L
R1=10
R2
10
C
22 de Fevereiro de 2000