Lista1: Cinemática Unidimensional

Lista2: Cinemática Unidimensional
Lista 2: Cinemática Unidimensional
NOME:______________________________________________________________________
Matrícula:
Turma:
Prof. :
Importante:
i. As cinco páginas seguintes contém problemas para serem resolvidos e entregues.
ii. Ler os enunciados com atenção.
iii. Responder a questão de forma organizada, mostrando o seu raciocínio de forma coerente.
iv. Analisar a resposta respondendo: ela faz sentido? Isso lhe ajudará a encontrar erros!
1.
Um carro trafegando à velocidade de 30 km/h, está à distância de 50 m de uma avenida cuja largura é
de 30 m quando o sinal de cruzamento com a avenida fica amarelo. Sabe-se que o sinal fica amarelo
durante 6,0 s. A aceleração máxima do carro é de 2,3 m/s², e o motorista tem um tempo de reação de
0,60 s antes de acelerá-lo. Conseguirá o veículo cruzar a avenida antes do sinal ficar vermelho?
1
Lista2: Cinemática Unidimensional
2. No laboratório foi realizada uma medida da aceleração de queda livre g lançando-se uma bola de vidro
para cima em um tubo evacuado e deixando-a retornar. Seja TL na figura o intervalo de tempo entre
duas passagens da bola através de certo nível inferior, TU o intervalo de certo tempo entre as duas
passagens por um nível superior e H a distância entre os dois níveis. Mostre que g = 8 H/(T2L-T2U) .
2
Lista2: Cinemática Unidimensional
3. Um objeto é jogado verticalmente e tem velocidade ascendente de 25 m/s quando atinge um quarto de
sua altura máxima acima do ponto de lançamento. Qual é a velocidade escalar inicial (de lançamento)
do objeto?
3
Lista2: Cinemática Unidimensional
4. Para medir a aceleração da gravidade na Lua, onde não existe atmosfera, uma equipe de exploradores
usa o experimento ilustrado na figura. Um dispositivo atira uma esferinha verticalmente para cima a
partir da altura y = 0, e envia um sinal a um relógio para iniciar a contagem do tempo. Na altura y = h,
um feixe de laser é interceptado pela esferinha, no instante t1 quando ela sobe e no instante t2 quando
ela desce. A interrupção da luz no detector gera um sinal enviado ao relógio, que registra os tempos t1
e t2. Calcule o valor de g a partir dos dados obtidos no experimento.
4
Lista2: Cinemática Unidimensional
5. Você joga um balão d’água da janela de seu quarto, 80,0 m acima da cabeça de seu amigo. Em 2,00 s
após jogar o balão, sem perceber que tem água dentro, seu amigo dispara um dardo de uma pistola,
que está na mesma altura que sua cabeça, diretamente para cima em direção ao balão com uma
velocidade inicial de 20,0 m/s.
(a) Em quanto tempo o dardo explodirá o balão após ele ser solto?
(b) Quanto tempo após o dardo atingir o balão seu amigo terá que sair do caminho da água que cai em
sua direção? Presuma que o balão freia instantaneamente no contato com o dardo.
5
Lista2: Cinemática Unidimensional
Questões:
(A) A figura mostra o gráfico da posição versus tempo para o movimento dos objetos A e B que se movem
sobre o mesmo eixo.
(a) No instante t = 1 s, a velocidade de A é maior, menor ou igual à velocidade de B? Explique
(b) Em algum instante A e B possuem a mesma velocidade? Em caso afirmativo em que instante ou
instantes? Explique.
(B) Um carro trafega para o norte. Seu vetor aceleração pode apontar para o sul? Explique.
(C) Um objeto é lançado com velocidade vo para cima de uma altura h. Mostre que a velocidade com que
ele passa, no retorno, pela posição de lançamento é a mesma em módulo.
(D) Um objeto é lançado para cima de uma altura h. Mostre que o tempo para que ele retorne à sua posição
inicial de lançamento é igual ao dobro do tempo que o objeto leva para atingir sua posição máxima.
(E) Uma pessoa em pé borda de um penhasco, a uma certa altura acima do solo, lança uma bola
verticalmente para cima com velocidade escalar inicial v0; depois lança outra bola verticalmente para
baixo, com a mesma velocidade inicial. Que bola terá maior velocidade escalar ao atingir o solo.
Despreze a resistência do ar.
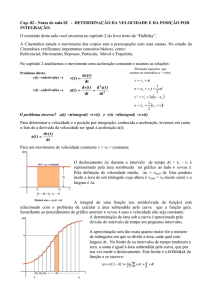
Exercícios e Problemas
Exercício corrigido em aula de monitoria.
1) A posição de uma partícula movendo-se ao longo do eixo x depende do tempo de acordo com a
expressão,
, onde x é dado em metros e t em segundos.
(a) Quais as unidades dos coeficientes 3,0 e 1,0 da equação x(t)?
(b) Para que instante t a partícula atinge a posição máxima?
(c) Qual é a velocidade média durante os primeiros 2,5s? É possível conhecer o sentido do
movimento? Explique.
(d) Qual é a velocidade instantânea v(t) em 2,5s? É possível conhecer o sentido do movimento?
Explique.
(e) Trace o gráfico de x versus t para t = 0 a t= 4,0 s e indique como as respostas de (c) e (d) podem
ser encontradas no gráfico.
6
Lista2: Cinemática Unidimensional
2) Uma partícula parte da origem em t = 0 e se move ao longo eixo x. O gráfico da velocidade da
partícula em função do tempo é mostrado na figura. (a) Em que intervalo de tempo a aceleração é
positiva, negativa ou nula? (b) Qual é a distância percorrida pela partícula em 16s?
3) Uma pedra é atirada diretamente para cima com velocidade de 20 m/s. Ao retornar ela cai em um
buraco com 10 m de profundidade.
(a) Qual é a velocidade da pedra no fundo do buraco?
(b) Que distância ela percorreu no ar desde o instante em que foi liberada até bater no fundo do
buraco?
4) Em t=0, um alpinista, de forma acidental, deixa um grampo cair livremente em um ponto alto de um
paredão de rocha até um vale abaixo. Após um curto intervalo de tempo, seu companheiro de
escalada, que está 10 m acima dele no paredão, lança
outro grampo para baixo. As posições y dos grampos
versus t durante as quedas são dadas na figura. Com que
velocidade o segundo grampo foi lançado?
5) Uma estudante lança um jogo de chaves verticalmente
para cima para sua colega de república, que está em uma
janela 4,00 m acima. A segunda estudante pega as chaves 1,50 s depois. (a) Com que velocidade
inicial as chaves foram lançadas? (b) Qual era a velocidade das chaves imediatamente antes de
serem pegas?
Exercício corrigido em aula de monitoria.
6) A velocidade de uma partícula em movimento ao longo do eixo x varia no tempo de acordo com a
expressão
, em que t está em segundos.
(a) Encontre a aceleração média no intervalo de tempo de t = 0 até t = 2,0 s.
(b) Determine a aceleração em t = 2,0 s.
7) Um esquiador está deslizando a 3,0 m/s sobre uma pista de neve horizontal e sem atrito.
Subitamente ele começa a descer uma rampa com inclinação de 10º. Na base da mesma, sua
velocidade é de 15 m/s.
(a) Qual é o comprimento da rampa?
(b) Quanto tempo ele leva para chegar à base da rampa?
7
Lista2: Cinemática Unidimensional
8) Uma partícula move-se ao longo do eixo x e tem sua velocidade descrita pela função
m/s,
onde t está em segundos. A posição inicial é
em
. Em t = 1 s, qual é (a) a posição,
(b) a velocidade e (c) a aceleração da partícula?
9) Uma patinadora veloz move-se sem atrito sobre o gelo liso a 8,0 m/s quando passa para um trecho
de 5,0 m com gelo rugoso. Ela desacelera uniformemente, depois prossegue a 6,0 m/s. Qual é sua
aceleração no trecho rugoso.
10) Três partículas se movem ao longo do eixo x, cada uma tendo partido com v0 = 10 m/s em t0 = 0 s. O
gráfico A é de posição versus tempo; o gráfico B da velocidade versus tempo; e o C, da aceleração
versus tempo. Determine a velocidade de cada partícula no instante t = 7,0 s. Trabalhe com a
geometria dos gráficos, e não com as equações cinemáticas.
8
Lista2: Cinemática Unidimensional
RESPOSTAS:
1) (a) [3,0] = [m/s2]; [1,0] =[m/s3]; (b) 2 s; (c) 1,3 m/s; (d) – 3,8 m/s
2) (a) 0 – 2 s: positiva, 2 s – 10 s: nula; 10 s – 12 s: negativa, 12 s – 16 s: nula, (b) 68 m.
3) (a) 24 m/s; (b) 4,5 s
4) 17 m/s
5) (a) 10,0 m/s para cima; (b) 4,68 m/s para baixo.
6) (a) – 10 m/s²; (b) – 20 m/s²
7) (a) 64 m; (b) 7,1 s.
8) (a) 1,7 m; (b) 2,0 m/s; (c) 4,0 m/s².
9) -2,8 m/s²
10) vA = - 10 m/s; vB = - 20 m/s; vC = 75 m/s.
9