Física 3 - Cobertura Máxima GGE

Gabaritos e Justificativas
Segunda Etapa
Física 3 
COMISSÃO DE PROCESSOS
SELETIVOS E TREINAMENTOS
Fone: (81) 3231-4000
Fax: (81) 3231-4232
Física 3
Valores de Algumas Grandezas
Aceleração da gravidade: 10 m/s2
Velocidade das ondas eletromagnéticas no vácuo: 3 x 10 8m/s
K=
1
= 9 x 109
4  o
N.m2
C2
Calor específico do gelo: 0,5
cal
gC
Calor latente de fusão do gelo: 80 cal/g

0°
30°
45°
60°
90°
sen 
0
1
2
2
2
3
2
1
cos 
1
3
2
2
2
1
2
0
01. Um estudante numa janela de um edifício observa que um objeto lançado para
cima gasta 4,0 s para retornar a passar pela janela. Calcule a altura máxima
atingida pelo objeto, em m, acima da janela de observação do estudante.
Despreze o atrito do objeto com o ar.
Resposta: 20
Justificativa:
Com o eixo vertical y, orientado para cima e com origem na altura da janela,
tem-se
v = vyo – gt. O tempo de subida é igual ao tempo de descida portanto,
0 = vyo – 10  2  vyo = 20 m/s.
Por outro lado, usando a equação de Torricelli tem-se que
v2 = vyo2 – 2 g y  02 = 202 – 2  10  (y – 0). Logo, y = 20 m.
02. A figura mostra a variação da velocidade escalar de dois pequenos blocos que
se movem em sentidos opostos, na direção vertical. No instante em que o bloco
A cai do alto de um edifício de 94 m de altura, o bloco B é lançado a partir do
solo, ao longo da mesma linha vertical. Qual é a distância entre os blocos, em
m, no instante em que as suas velocidades escalares têm o mesmo valor?
Despreze a resistência do ar.
Resposta: 14
Justificativa:
O instante em que vA = vB = v = 20 m/s é t = 2,0 s
Distância percorrida por A  Área = (1/2)  20  2 = 20 m = xA
Distância percorrida por B  Área = (1/2)  (40 + 20)  2 = 60 m = xB
Distância entre A e B = H – (xA + xB) = 94 – 80 = 14 m
03. Uma brincadeira de tiro ao alvo consiste em acertar, a partir do ponto O, uma
pequena esfera de ferro presa por um ímã, em P, como mostra a figura. No
instante em que é feito um disparo, a esfera se desprende, sendo
eventualmente atingida durante a queda. Se um projétil é disparado a 100 m/s e
acerta o alvo, qual é a distância percorrida pelo alvo, em cm, antes que ele seja
atingido? Despreze a resistência do ar.
PQ  H  6 m
OQ  D  8 m
P
H
Vo
O
D
Q
Resposta: 5
Justificativa:
Com a origem do sistema de coordenadas em O, temos:
Alvo  XA = D; YA = H – 1/2 gt2
Projétil  XP = (Vo cos ) t; YP = (Vo sen) t - 1/2 gt2
Fazendo XP = XA e YP = YA, obtemos t =
(D 2  H2 )
para o tempo de queda.
Vo
Portanto, distância de vôo do alvo = 1/2 gt2 = 1/2 x 10 x
(D 2  H2 )
Vo2
= 5 cm
04. Um bloco de massa igual a 6,3 kg é pendurado por uma corda como mostrado
na figura. Calcule a força máxima, em N, que pode ser aplicada na corda
inferior tal que a corda superior não rompa. As cordas utilizadas suportam uma
tensão máxima de 100 N. Considere as massas das cordas desprezíveis em
comparação com a massa do bloco.
cordas
Resposta: 37
Justificativa:
A tensão que atua na corda superior é dada por Tsuperior = P + Tinferior,
onde P é o peso do bloco.
Portanto, o valor máximo de Tinferior corresponderá a Tsuperior = 100 N
ou seja, Tinferior = Tsuperior - P = 100  6, 3  10 = 37 N
05. Um objeto desliza sobre um plano horizontal com atrito. Observa-se que o
objeto desliza 8,0 m em 2,0 s, desde o lançamento até parar. Calcule o
coeficiente de atrito cinético entre o objeto e o plano, em potência de 10 -1.
Considere constante a força de atrito entre o objeto e o plano, e despreze o
atrito do objeto com o ar.
Resposta: 4
Justificativa:
Tem-se um movimento uniformemente variado logo y = yo + vot – at2/2.
Logo,  y = 8 = 2 vo – 2 a
(1)
Além disto, v = vo – at  0 = v o – 2a (2)
Resolvendo o sistema de equações (1) e (2) tem-se que:
a = 4 m/s2 e vo = 8 m/s.
Fresultante = ma = Fatrito = c mg  c = a/g = 0,4 = 4  10-1
06. Um pequeno corpo A, de massa mA = M, inicia seu movimento a partir do
repouso, de uma altura H, e desliza em uma pista sem atrito como indicado na
figura. Na parte horizontal da pista, ele colide com outro pequeno corpo B, de
massa mB = 6 M, que se encontra em repouso no ponto P. Se a colisão é
completamente inelástica, os dois corpos aderem um ao outro e se elevam até
uma altura h. Qual é a razão H/h ? Despreze a resistência do ar.
mA
H
mB
h
P
Resposta: 49
Justificativa:
Velocidade de A, antes da colisão:
1
m VA2 = mgH  VA = 2gH
2
Velocidade de (A + B) depois da colisão:
2gH
V
(mA + mB) V = mAVA  V = A =
7
7
Altura final de (A + B): (mA + mB)gh = 1/2 (mA + mB) V2  V = 2gh
Portanto:
2gH
H
 2gh   49
7
h
07. O eixo de um motor que gira a 3600 rotações por minuto é frenado,
desacelerando uniformemente a 20  rad/s2, até parar completamente. Calcule
quanto tempo foi necessário, em s, para o motor parar completamente.
Resposta: 6
Justificativa:
A equação para a velocidade angular é dada por
 = o  t = 60  (2 )  20 t = 0  t = 6 s
08. Uma esfera homogênea de massa m = 400 g e raio r = 6 cm é colocada no
interior de uma esfera oca de massa M = 200 g e raio R = 12 cm. O sistema
está inicialmente em repouso sobre uma superfície horizontal, na posição
indicada na figura abaixo. Quando a esfera menor é solta, ela rola no interior da
esfera oca até parar. Determine, em cm, a altura final do centro de massa do
sistema em relação à superfície horizontal.
r
R
Resposta: 8
Justificativa:
O centro de massa é dado por YCM = (m1  y1 + m2  y2 )/(m1 + m2).
Após um período de tempo em que o conjunto oscila, a esfera no interior
encontra o repouso na posição mais baixa da esfera maior.
Nesta situação, YCM = (400  6 + 200  12)/(400 + 200)
YCM = 8 cm.
09. Uma caixa cúbica metálica de 10  está completemente cheia de óleo, quando a
temperatura do conjunto é de 20°C. Elevando-se a temperatura até 30°C, um
volume igual a 80 cm3 de óleo transborda. Sabendo-se que o coeficiente de
dilatação volumétrica do óleo é igual a 0,9 x 10-3°C-1, qual é o inteiro mais
próximo do valor do coeficiente de dilatação linear do metal, em unidades de
10-6 °C-1?
Resposta: 33
Justificativa:
Dilatação do recipiente = VoT - Volume do óleo derramado.
Dilatação do recipiente = 10 4 x 0,9 x 10-3 x 10 - 80 = 10 cm3.
Portanto, 10 cm3 = 3 metal.Vcaixa. T
3  = 10-4  33,3 x 10-6°C-1
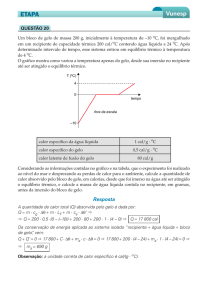
10. Em um experimento, um estudante coloca num recipiente um cubo de gelo, de
massa igual a 1000 g e temperatura de –10°C. Aquecendo o conjunto, o
estudante observou que em um dado instante havia uma mistura de 900 g de
gelo e 100 g de água, tudo à temperatura de 0 °C. Calcule a energia térmica,
em kcal, necessária para fundir as 100 g de gelo, partindo das1000 g iniciais.
Resposta: 13
Justificativa:
O calor absorvido pelo gelo para levá-lo de –10ºC até 0ºC é dado por
Q = mcT = 1000  0, 5  (0 – (–10)) = 5000 cal.
O calor absorvido pelo gelo a 0ºC para fundir a massa de 100 g a 0 ºC é dado
por Q = mLf = 100  80 = 8000 cal.
O calor total absorvido pela substância é a soma das quantidades de calor
calculados acima, Q = 13000 cal = 13 kcal.
11. Duas lentes biconvexas delgadas, de distâncias focais 1 = 20 cm e 2 = 30 cm,
são postas em contato, como indicado na figura. O conjunto se comporta como
uma única lente convergente, cuja distância focal depende de 1 e 2. Calcule a
distância focal do conjunto, em cm.
1
Resposta: 12
Justificativa:
2
Uma imagem formada pela lente 1 serve como objeto para a lente 2.
Escrevendo a equação de formação de imagens para cada lente verificamos
que tudo se passa como se tivéssemos uma única lente cuja distância focal
1
1
1
satisfaz a 

 1  2
Portanto,
1
1
1
  = 12 cm


 20 30
12. Um gerador de microondas emite ondas planas que se propagam no vácuo,
para a direita, sendo 100% refletidas de volta para o gerador, como mostrado
na figura. Estas ondas interferem, formando um padrão de onda estacionária.
Se as posições de mínimos sucessivos estão separadas por 5 cm, qual é a
freqüência da microonda, em unidades de 109 Hz?
Ondas
propagantes
~
Antena do gerador de
microondas
Refletor perfeito
Resposta: 3
Justificativa:
Dois pontos de mínimos sucessivos distam de /2;
portanto,  = 10 cm

3x108
10x10 2
 3x109 Hz
13. Duas cargas puntiformes no vácuo, de mesmo valor Q = 125 C e de sinais
opostos, geram campos elétricos no ponto P (vide figura). Qual o módulo do
campo elétrico resultante, em P, em unidades de 107 N/C?
3 cm
-Q
3 cm
P
4 cm
+Q
Resposta: 54
Justificativa: O campo terá resultante na direção paralela à linha que une as
cargas
ER


+
ER = 2 Esen
sen = 3/5 = 0,6

125x10 6
ER = 2x  9 x 109
2

5x10 2





7
 x 0,6 = 54 x 10 N/C

14. Uma nuvem eletrizada está situada a 1000 m de altura, paralelamente à
superfície da Terra, formando com esta um capacitor plano de 15 nF. Quando o
campo elétrico no ar (entre a nuvem e a Terra) atinge o valor de 3,0 x 106 N/C,
ocorre um relâmpago. Calcule a carga elétrica, em C, que se encontrava
armazenada na nuvem, no instante da descarga elétrica.
Resposta: 45
Justificativa:
Quando ocorrer o relâmpago a diferença de potencial será
V = E.d = (3x106) x 1000 = 3 x 10 9 V
A carga será então Q = CV = 15 x 10-9 x 3 x 109 = 45 C.
15. Uma bateria foi ligada a um resistor X de resistência ajustável, como indicado
na figura. Para diferentes valores da resistência, os valores medidos para a
diferença de potencial VAB, entre os pontos A e B, e para a corrente i no
circuito, são indicados no gráfico abaixo. Determine o valor da resistência
interna r da bateria, em .

A
r
B
A
X
Resposta: 5
Justificativa:
VAB =  - ri
Quando i = 0  VAB =  = 6,0 V (obtida do gráfico)
Usando o gráfico, vemos que quando i = 0,4A temos VAB = 4,0 V.
Portanto, 4 = 6 – r x 0, 4  r = (6-4)/(0,4) = 5 
16. Um fio MN, de 40 cm de comprimento e massa igual a 30 g, está suspenso
Linhas do campo
magnético
horizontalmente por uma mola ideal de constante elástica k = 10 N/m. O
conjunto encontra-se em uma região de campo magnético uniforme B =
0,1 Wb/m2, como indicado na figura. Quando a corrente no fio for 10 A, dirigida
de N para M, atuará sobre o fio uma força magnética dirigida verticalmente para
baixo. Determine a elongação total, devido à força magnética e à força
gravitacional, sofrida pela mola, em cm.
i = 10 A
M
N
Resposta: 7
Justificativa:
Força magnética sobre o fio MN = Bil = 0,1 x 10 x 0,4 = 0,4 N
Peso do Fio: mg = 30 x 10-3 x 10 = 0,3 N
x
mg  Bil 0,3  0,4

 7 cm
k
10