setor 1201

setor 1201
12010508
Aula 39
CHOQUE CONTRA OBSTÁCULO FIXO
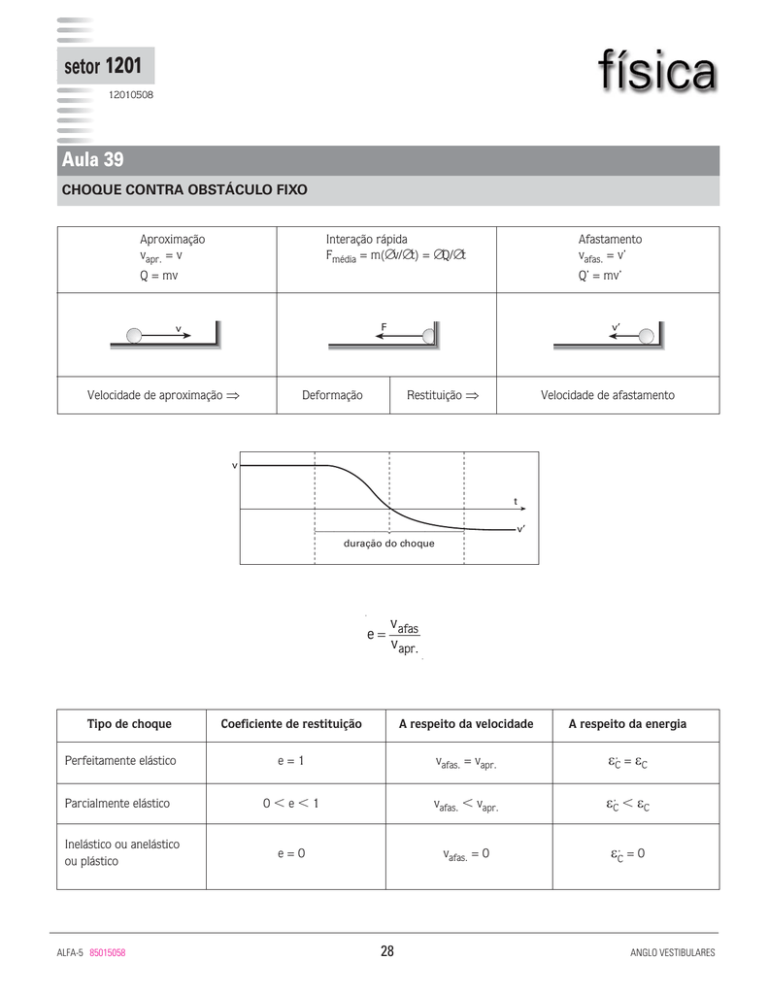
Aproximação
vapr. = v
Interação rápida
Fmédia = m(∆v/∆t) = ∆Q/∆t
Afastamento
vafas. = v’
Q = mv
Q’ = mv’
F
v
Velocidade de aproximação ⇒
v’
Restituição ⇒
Deformação
Velocidade de afastamento
v
t
144444424444443
duração do choque
v’
v
e = afas
v apr.
Tipo de choque
Coeficiente de restituição
A respeito da velocidade
A respeito da energia
Perfeitamente elástico
e=1
vafas. = vapr.
εC’ = εC
Parcialmente elástico
0e1
vafas. vapr.
εC’ εC
e=0
vafas. = 0
εC’ = 0
Inelástico ou anelástico
ou plástico
ALFA-5 85015058
28
ANGLO VESTIBULARES
Exercício
Uma bola de bilhar de massa 0,4 kg, movimentando-se a
uma velocidade 10m/s, choca-se frontalmente contra a tabela da mesa. A respeito dessa colisão sabe-se que teve um centésimo de segundo de duração e apresenta um coeficiente de
restituição 0,8.
Determine:
a) A velocidade da bola imediatamente após a colisão.
b) A força média durante o choque.
c) A energia dissipada durante o choque.
d) Esboçar os gráficos da velocidade e da energia cinética
durante o choque.
v1
a) e = –
v’1
v’1
⇒ v’1 = –ev1 = – 8 m/s
v1
b)
F
+
– FM = ∆Q/∆t
FM = –
m(v’1 – v1)
∆t
⇒ FM = 720 N
c) εc = 1 mv2 = 20 J
2 1
εc = 1 mv’ 2 = 12,8 J
1
2
εdiss = Iεc – ε’ci = 7,2 J
ORIENTAÇÃO DE ESTUDO
d)
v(m/s)
Livro 1 — Unidade IV
10
Caderno de Exercícios — Unidade IV
t
–8
Tarefa Mínima
εC (J)
• Resolva o exercício 1, série 4.
20
Tarefa Complementar
12,8
• Resolva os exercícios 2, 3 e 4, série 4.
ALFA-5 85015058
29
ANGLO VESTIBULARES
Aulas 40 a 42
CHOQUE FRONTAL
Aproximação
vapr. = vA – vB
Q = mAvA + mBvB
vA
Interação rápida
Fmédia = m(∆v/∆t) = ∆Q/∆t
(para qualquer um dos corpos)
mAvA + mBvB = mAv’A + mBv’B
vB
F
Velocidade de aproximação ⇒
Afastamento
vafas. = v’B – v’A
Q’ = mAv’A + mBv’B
F
v’A
Restituição ⇒
Deformação
v’B
Velocidade de afastamento
vA
v’B
vapr.
vafas.
vB
144444424444443
duração do choque
v’A
t
v
e = afas
v apr.
Tipo de choque
Coeficiente de restituição
A respeito da velocidade
A respeito da energia
Perfeitamente elástico
e=1
vafas. = vapr.
ε’C = εC
Parcialmente elástico
0e1
vafas. vapr.
ε’C εC
e=0
vafas. = 0
ε’C εC
Inelástico ou anelástico
ou plástico
ALFA-5 85015058
30
ANGLO VESTIBULARES
2. Uma esfera A de massa m desliza sobre uma superfície lisa
e horizontal com velocidade vA. Choca-se, então, frontalmente com outra esfera B, idêntica a ela, que se encontra
em repouso. Sabendo-se que o choque é perfeitamente
elástico determine as velocidades v’A e v’B das esferas após
a colisão.
Exercícios
1. Uma esfera A de massa 2 kg e velocidade 10 m/s, choca-se
frontalmente com outra esfera B de massa 3 kg e velocidade 5 m/s em sentido contrário. Sabendo que o coeficiente de restituição desta colisão vale 1/6, determinar as velocidades finais das esferas.
m ⋅ vA + m ⋅ vB = m ⋅ v’A + m ⋅ v’B
vA + vB = v’A + v’B (1)
vB = – 5 m/s
e=
mA ⋅ vA + mB ⋅ vB = mA ⋅ v’A + mB ⋅ v’B
2 ⋅ 10 + 3(– 5) = 2 v’A + 3 v’B
2 v’A + 3 v’B = 5 (1)
e=
v’A – v’B
=1
vB – vA
v’A – v’B = vB – vA (2)
(1) + (2)
v’A + v’B = vA + vB (1)
v’A – v’B = vB – vA (2)
2v’A = 2 vB
v’A – vB = 0
v’A – v’B
1
=
⇒
vB – vA
6
vB – vA = 6(v’A – v’B)
6(v’A – v’B) = – 15 (2)
Substituindo em (1)
vB + v’B = vA + vB
v’B = vA
Resolvendo o sistema constituído pelas equações 1 e 2
v’A = 0,5 m/s
v’B = 2 m/s
CONCLUSÃO
frontal
elástico
mesma massa
v(m/s)
10
123
vA = 10 m/s
mA ⋅ vA + mB ⋅ vB = mA ⋅ v’A + mB ⋅ v’B
permuta de velocidade
2
v(m/s)
– 0,5
vA
5
vB = 0
ALFA-5 85015058
31
v’B = vA
v’A = vB = 0
ANGLO VESTIBULARES
3. Um corpo A é lançado em um plano horizontal sem atrito
com velocidade vA = 4,0 m/s. O corpo A, cuja massa é
mA = 2,0kg, colide com a esfera B, de massa mB = 5,0kg.
Inicialmente a esfera encontra-se parada e suspensa por
um fio flexível e inextensível de comprimento L e fixo em
O, e atinge a altura hB = 0,20 m, após a colisão.
a) Qual a velocidade v’B, da esfera B, imediatamente após
a colisão?
b) Qual o módulo e o sentido da velocidade v’A do corpo A
após a colisão?
c) Qual a diferença entre a energia mecânica do sistema
antes e depois da colisão?
d) A colisão foi perfeitamente elástica? Justifique.
O
hB
A
vA
B
a) Imediatamente após a colisão a esfera B sobe até hB.
O sistema não é isolado (o peso e a tração não se
equilibram e são forças externas), porém é conservativo, pois só forças conservativas realizam trabalho:
MB ⋅ v’B2 + 0 = 0 + MB ⋅ g ⋅ hB
(1/2) v’B2 = 10 ⋅ 0,20
v’B = 2 m/s
ORIENTAÇÃO DE ESTUDO
b) Na colisão as forças trocadas são internas, conseqüentemente o sistema é isolado:
MA ⋅ vA + MB ⋅ vB = MA ⋅ v’A + MB ⋅ v’B
Livro 1 — Unidade IV
Caderno de Exercícios — Unidade IV
2 ⋅ 4 + 0 = 2 ⋅ v’A + 5 ⋅ v’B
v’A = – 1 m/s
|v’A| = 1 m/s em sentido contrário ao inicial.
c)
(εMEC)ANTES = 1/2 MAv2A = 16J
(εMEC)DEPOIS = 1/2 MAv’ A2 + 1/2
(∆εMEC) = 5J
Tarefa Mínima
AULA 40
•
•
MB v’ B2 = 11 J
Leia os itens 1 a 8, cap. 2.
Resolva os exercícios 13 a 16, série 4.
AULA 41
•
Resolva os exercícios 17 a 19, série 4.
d) Não, pois houve variação da energia mecânica.
AULA 42
•
Resolva os exercícios 20 e 27, série 4.
Tarefa Complementar
AULA 42
•
ALFA-5 85015058
32
Resolva os exercícios 10 a 12 e 21 a 24, série 4.
ANGLO VESTIBULARES
Aulas 43 a 45
CONDIÇÕES DE EQUILÍBRIO DE UM CORPO
MOMENTO DE UMA FORÇA
→
Uma→força F está aplicada a um ponto P de um corpo. O momento
(M)O de F em relação a um ponto (O) é definido pela expressão:
Fy
F
(MF)O = (Fy) ⋅ (OP)
P
sendo:
0
→
Fy: a componente de F perpendicular à OP
→
+ se, sob ação exclusiva de F , o corpo adquirir movimento de rotação
no sentido anti-horário; →
– se, sob ação exclusiva de F , o corpo adquirir movimento de rotação
no sentido horário.
F
Podemos deslocar uma força ao longo de sua la. Portanto o momento
também pode ser calculado por:
Q
P
(MF)O = (F) ⋅ (OQ)
0
sendo:
la
OQ a distância entre o ponto O e la (braço do momento).
→
→
→
→
ROTAÇÃO EM TORNO DE UM EIXO FIXO DE UM CORPO SOB AÇÃO DE VÁRIAS FORÇAS ( F, G, H, T …)
Tomando-se os momentos em relação ao ponto O:
ΣM = MF + MG + MH + MT...
→
→
F
Podem acontecer 3 casos:
T
→
ΣM 0: o corpo gira no sentido anti-horário;
ΣM 0: o corpo gira no sentido horário;
ΣM = 0: o corpo NÃO GIRA.
G
O
→
H
CONDIÇÕES DE EQUILÍBRIO DE UM SÓLIDO:
ΣF = 0 (para que não haja translação) (1)
ΣM = 0 (para que não haja rotação) (2)
ALFA-5 85015058
33
ANGLO VESTIBULARES
2. A barra da figura tem peso desprezível e pode girar livremente em torno da articulação S. Supondo g = 10 m/s2,
que a barra esteja na posição horizontal, que o dinamômetro esteja na vertical e que M = 100kg, determinar:
a) a indicação do dinamômetro;
b) a força exercida pela articulação na barra.
Exercícios
1. A barra AB tem peso desprezível e pode girar livremente
em torno da articulação O. Sabendo-se que o peso do corpo 1 é 600 N e que y = 3x, determinar:
a) o peso do corpo 2 para que a barra fique em equilíbrio;
b) a força que a articulação exerce na barra.
y
x
A
B
O
S
P2
10 cm
R
40 cm
P1
M
F
x
y
A
B
T
P2
S
P1
10 cm
F
a) P1 ⋅ x – P2 ⋅ y = 0
600 ⋅ x = P2 ⋅ y
600 ⋅ (x/y) = P2
P2 = 200N
M
a) – (Mg 50) + T ⋅ 10 = 0
T = 5 Mg
T = 5000 N
b) T = F + Mg
F = T – Mg
F = 4000 N
b) F = P1 + P2
F = 800N
ALFA-5 85015058
R
40 cm
34
ANGLO VESTIBULARES
→
4. (UFPE) Uma menina de 50kg (peso 500N) caminha sobre
uma prancha com 10m de comprimento e massa desprezível. A prancha está apoiada em suas extremidades, nos pontos A e B, como mostra a figura. Pede-se construir os gráficos das forças verticais exercidas sobre a barra pelos apoios
A e B em função da distância x entre a menina e o ponto A.
3. Um bloco de peso P é suspenso por fios, como se indica
na figura. Determinar:
→
a) A intensidade da força F , horizontal.
b) A intensidade da força de tração no fio AB.
c) Supondo que os 3 fios sejam idênticos, qual deles seria
o mais provável de se romper?
A
θ
→
B
NA
F
NB
A
B
10 m
Se as la de todas as forças que agem em um corpo
inicialmente em repouso, passam por um único ponto,
esse corpo não pode adquirir movimento de rotação.
Portanto pode ser tratado como um ponto material. A
condição de equilíbrio é somente que:
ΣF = 0 (para não haver translação).
Para que a resultante das forças que agem no corpo
seja nula:
NA + NB = P
NA + NB = 500 (1)
A soma dos momentos em relação ao ponto A (ou em
relação a qualquer ponto) tem de ser nula.
– P(x) + NB ⋅ 10 = 0
NB = 50x (2)
T
F
P
500
NA; NB (N)
a) F
NB = 50x
b) cos θ = P/T
T = P/cos θ
5
T
P θ
NA = 500 – 50x
250
c) O que suportar maior força, que é o fio AB
Observe que T é a hipotenusa do triângulo. Portanto T
é a maior das forças.
x (m)
10
F
ALFA-5 85015058
35
ANGLO VESTIBULARES
5. No sistema esquematizado nas figuras a seguir, o peso da
barra é desprezível. Nessas condições:
a) Determinar x, em função de m1, m2, x1 e x2 para que
o sistema da figura a permaneça em equilíbrio.
b) O sistema da figura b está em equilíbrio?
c) Preencher:
Centro de massa de um sistema (ou de um corpo) é o
ponto onde se pode imaginar concentrada toda a
massa do sistema (ou do corpo).
6. (FUVEST/2002) Um avião, com massa M = 90 toneladas,
para que esteja em equilíbrio em vôo, deve manter seu centro de gravidade sobre a linha vertical CG, que dista 16 m
do eixo da roda dianteira e 4,0 m do eixo das rodas traseiras, como na figura abaixo. Para estudar a distribuição de
massas do avião, em solo, três balanças são colocadas sob
as rodas do trem de aterrisagem. A balança sob a roda dianteira indica MD e cada uma das que estão sob as rodas traseiras indica MT.
ND
figura a
2NT
CG
x2
x=?
g
x1
m1 + m2
m1
16 m
m2
Uma distribuição de massas, compatível com o equilíbrio do
avião em vôo, poderia resultar em indicações das balanças,
em toneladas, correspondendo aproximadamente a:
a) MD = 0 MT = 45
b) MD = 10 MT = 40
c) MD = 18 MT = 36
d) MD = 30 MT = 30
e) MD = 72 MT = 9,0
figura b
O
x
m1 + m2
4,0 m
C
x
m1 + m2
As condições de equilíbrio para um corpo extenso são:
ΣMO = 0 e ΣFy = 0
a) m1g x1 + m2g x2 = (m1 + m2) gx
m1 x1 + m2 x2 = (m1 + m2) x
x = (m1 x1 + m2 x2) / (m1 + m2)
Adotando-se o pólo em D e convencionando-se o sentido
anti-horário como positivo para o momento das forças:
ΣMD = 0: –P ⋅ 16 + 2NT ⋅ 20 = 0
b) SIM. Portanto podemos imaginar as massas m1 e m2
concentradas no ponto C, que dista x do ponto O tal
que:
x = (m1 x1 + m2 x2) / (m1 + m2)
ΣFy• = 0: ND + 2NT = P
ND + 2 ⋅ 360000 = 900000
ND = 180000 N
Como NT = 360000 N e ND = 180000 N, as indicações
correspondem às massas de 36 toneladas e 18 toneladas.
ALFA-5 85015058
36
ANGLO VESTIBULARES
ORIENTAÇÃO DE ESTUDO
Livro 1 — Unidade IV
Caderno de Exercícios — Unidade V
Tarefa Mínima
AULA 43
•
•
Leia os itens 1 a 5, cap. 3.
Resolva os exercícios 3, 4, e 10, série 1.
AULA 44
•
•
Leia os itens 6 a 12, cap. 3.
Resolva os exercícios 14 a 16 e 21, série 1.
AULA 45
•
Resolva os exercícios 25, 27 e 29, série 1.
Tarefa Complementar
AULA 45
•
ALFA-5 85015058
37
Resolva os exercícios 19, 22 a 24, 28 e 30 a 33, série 1.
ANGLO VESTIBULARES