LISTA 30º cap 11 Exercícios Adicionais

Universidade Tecnológica Federal do Paraná UTFPR
Disciplina de Física I
Prof. Nelson Elias
37ª Lista de Exercícios: Cap. 10 Rotação e Momento de Inércia. Exercícios Adicionais.
Aluno: _________________________________________ Turma: _______ Data: ______/_____/______.
1) Para t = 0 a corrente de um motor elétrico de corrente contínua (dc) é invertida, produzindo um deslocamento angular
do eixo do motor dado por:
θ(t) =(250 rad/s)t – (20.0 rad/s2)t2 – (1.50 rad/s3)t3
a) Em que instante a velocidade angular do eixo do motor se anula?
b) Calcule a aceleração angular no instante em que a velocidade angular do eixo do motor é igual a zero.
c) Quantas revoluções foram feitas pelo eixo do motor desde o instante em que a corrente foi invertida até o momento
em que a velocidade angular se anulou?
d) Qual era a velocidade angular do eixo do motor para t = 0s, quando a corrente foi invertida?
e) Calcule a velocidade angular média no intervalo de tempo desde t = 0s até o instante calculado no item (a).
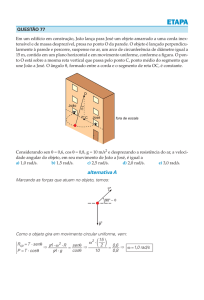
2) Uma corda leve e flexível é enrolada diversas vezes na periferia de uma casca cilíndrica com raio de 0,25 m e massa
igual a 40,0 N, que gira sem atrito em torno de um eixo horizontal fixo. O cilindro é ligado ao eixo por meio de raios
com momento de inércia desprezíveis. O cilindro está inicialmente em repouso. A extremidade livre da corda é puxada
com uma força F constante até uma distância de 5,00 m, e nesse ponto a extremidade da corda se move a 6,00 m/s.
Sabendo que a corda não desliza sobre o cilindro, qual é o valor da força F?
3) Uma roda de bicicleta com raio igual a 0,33 m gira com aceleração angular dada pela expressão:
α(t) = γ - βt , onde γ = 1,80 rad/s2 e β = 0,25 rad/s3. Ela está em repouso para t = 0 s.
a) Determine as expressões para a velocidade angular e deslocamento angular em função do tempo.
b) Calcule a velocidade angular positiva máxima e o deslocamento angular positivo máximo da roda.
4) A polia indicada na figura possui raio 0,160 m e momento de inércia de 0,480 kg.m2. A corda não desliza sobre a
periferia da polia. Use métodos de conservação da energia para calcular a velocidade do bloco de 4,00 kg
no momento em que ele atinge o solo.
4,00 kg
5,00m
2,00 kg
5) Um pneu, com raio R = 25 cm e massa M = 900 g, gira em torno de um eixo central fixo, à velocidade de 600
rev/min. Qual a energia cinética de rotação deste pneu em joules ? (*considere um aro para uma aproximação do momento de inércia
do pneu). Resp. K = 110,42 J
6) A figura abaixo apresenta um bloco de massa M = 500 g, e outro de massa m = 460 g,
a roldana que está montada em mancais sem atrito, tem um raio de 5,00 cm.
Considere que o sistema começa na se mover na posição indicada pela figura.
Sabendo que o bloco mais pesado atinge o solo 5,0 s após iniciado o movimento.
Determine:
a) qual a aceleração dos blocos?
b) qual a tração na parte que sustenta o bloco mais pesado? e qual a tração na corda na parte que
sustenta o bloco mais leve?
c) qual a aceleração angular da roldana?
d) qual o momento de inércia da roldana?
m
M
75 cm
Respostas:
a) a= 0,06 m/s2, b) T1= 4,53 N, c) T2 = 4,87 N, d) α = 1,2 rad/s2 e e) I = 1,4.10-2 kg.m2
Resolução para o exercício 1.
ω =(250 rad/s) – (40.0 rad/s2)t – (4.50 rad/s3)t2,
α = -(40.0 rad/s2) – (9.00 rad/s3)t.
Fazendo-se ω = 0 resulta em uma equação quadrática em t;
o único valor de tempo positivo para o qual ω = 0 é t = 4,23 s.
Em t = 4,23 s, b) Em t = 4,23, α = -78.1 rad/s2. c) Em t = 4,23 s, θ = 586 rad = 93.3 rev.
a)
d) Em t = 0, ω = 250 rad/s.
ωm = 586 rad = 138 rad / s.
e)
4.23 s
Resolução para o exercício 2.
O trabalho realizado sobre o cilindro é PL, onde L é o comprimento da corda. Combinando as Equações (v = w.r), (K
=1/2 Iw2 ) e a expressão para I , ver Tabela casca cilíndrica (I = mr2),
temos: WFR = ΔK
W = trabalho = F . L
com v0 = 0
1
v2
1
FL = Iω 2 = FL = mR 2 2
2
R
2
ou
F=
1 Peso v 2 (40.0 N )(6.00 m / s) 2
=
= 14.7 N.
2 g L 2(9.80 m / s 2 )(5.00 m )
t
Resolução para o exercício 3.
a) Por integrações sucessivas das Equações ( v − v0 = ∫ a (t ) dt
t
)
t0
e ( x − x0 = ∫ v (t ) dt ),
β 2
t = (1.80 rad / s 2 )t − ( 0.125 rad / s 3 )t 2 .
2
γ
β
θ( t ) = t 2 − t 3 = ( 0.90 rad / s 2 )t 2 − ( 0.042 rad / s 3 )t 3 .
2
6
γ
t0
ω( t ) = γ t −
b) A velocidade angular positiva máxima ocorre quando (dω/dt =0) α = 0, ou t =
2
O deslocamento angular máximo ocorre quando(dθ/dt = 0)
2γ
β
; a velocidade angular para este
⎛ γ ⎞ β ⎛ γ ⎞ 1 γ 2 1 (1.80 rad / s 2 ) 2
ω = γ ⎜⎜ ⎟⎟ − ⎜⎜ ⎟⎟ =
=
= 6.48 rad / s .
3
⎝ β ⎠ 2 ⎝ β ⎠ 2 β 2 ( 0.25 rad / s )
tempo é:
t=
β
ω = 0,
para o tempo
(t = 0 é um ponto de inflexão e θ(0) não é um máximo) e o deslocamento angular para
este tempo é:
2
3
γ ⎛ 2γ ⎞ β ⎛ 2γ ⎞
2 γ 3 2 (1 .80 rad / s 2 ) 3
⎟ − ⎜⎜
⎟⎟ =
θ = ⎜⎜
=
= 62 .2 rad .
⎟
2⎝ β ⎠
6⎝ β ⎠
3 β 2 3 ( 0 .25 rad / s 3 )
Resolução para o exercício 4.
A energia potencial gravitacional que se transformou em energia cinética é:
K = (4.00 kg – 2.00 kg)(9.80 m/s2)(5.00 m) = 98.0 J.
Em termos da velocidade comum dos blocos, a energia cinética do sistema é:
1 ⎛v⎞
1
K = (m 1 + m 2 ) v 2 + I ⎜ ⎟
2 ⎝R⎠
2
2
1⎛
( 0.480 kg ⋅ m 2 ) ⎞
⎜
⎟⎟ = v 2 (12.4 kg.)
= v ⎜ 4.00 kg + 2.00 kg +
2
2⎝
(0.160 m ) ⎠
2
Resolvendo para v, temos:
v=
98.0 J
= 2,81 m / s.
12.4 kg