O Movimento Circular

O Movimento Circular
Prof. Rodrigo
O movimento circular está sempre presente em nossa vida
O conhecimento preciso sobre movimento circular
permitiu a construção dos satélites de comunicações
(artificiais) que giram em movimento circular e uniforme
em torno da Terra.
Sistema de Posicionamento global (GPS)
 rad  180
rad
  graus 

   rad
 180

Podemos fazer uma equivalência entre radianos e graus
para que o aluno se habitue a trabalhar com medida de
ângulo em radianos.
Exemplos:
Clique para apresentar conteúdo.
Por definição, o deslocamento angular Δθ (ângulo) é dado
pela razão entre o deslocamento escalar ΔS e o raio de
curvatura r.
 rad
S

r
S   rad   r
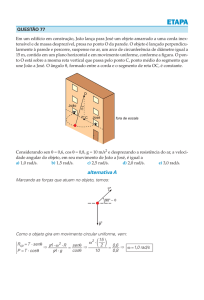
Consideremos um móvel que descreve um movimento
circular e uniforme (com velocidade constante) entre os
pontos P1 e P2 da trajetória abaixo, no sentido anti-horário.
 rad
S
V

t
t
Podemos definir a chamada velocidade angular média ωm
(ω = letra ômega) como sendo a razão entre o
deslocamento angular do móvel e o intervalo de tempo
desse deslocamento.
Clique para apresentar conteúdo.
No SI, a velocidade angular (ou pulsação) é dada em rad/s.
Em outros sistemas, pode ser uma unidade qualquer de
ângulo dividido por uma unidade de tempo.
Vamos relacionar as velocidades linear e angular:
 rad
S
S   rad   r  
V
t
t
 rad   r

S
V
V 

t
t
V r
Chamamos de período de um movimento circular e
uniforme ao intervalo de tempo necessário para que o
móvel complete uma volta na circunferência.
t
T
n
T  Período

t  interalo de tempo
n  número de voltas

Clique para apresentar conteúdo.
Chamamos de frequência de um movimento circular o
número de rotações realizadas por unidade de tempo.
No SI:
1
f 
T
n
f 
t
 f  frequência [hertz (Hz)] Hz = s 1

t  interalo de tempo [segundo (s)]
n  número de voltas

Todo objeto que descreve um movimento curvilíneo
apresenta um tipo muito especial de aceleração: a
centrípeta. Essa aceleração sempre aponta para o
centro
de
curvatura da trajetória e sempre é
perpendicular à reta tangente que passa pela posição que
o corpo ocupa.
2
V
ac 
r
ac    r
2
B
A
A
B
A
Observe que:
VA  VB
Logo:
 A  RA  B  RB
B
A
B
Observe que:
 A  B
Conclusão:
VA VB

Logo:
RA RB
f A  fB