Exercícios de Método das Forças (gab) - PDF

Lista de Exercícios
Método das Forças
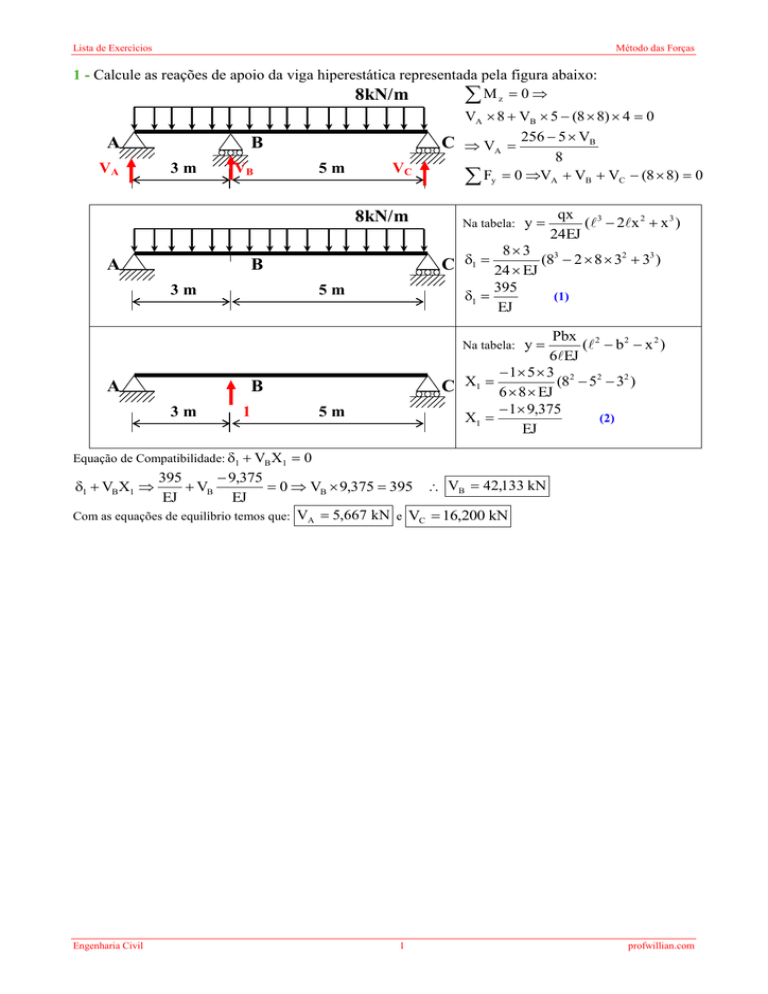
1 - Calcule as reações de apoio da viga hiperestática representada pela figura abaixo:
8kN/m
Mz  0 
A
VA
B
3m
VB
C
5m
VC
8kN/m
A
Na tabela: y 
83
qx
(3  2x 2  x 3 )
24EJ
3
2
3
C 1  24  EJ (8  2  8  3  3 )
B
3m
VA  8  VB  5  (8  8)  4  0
256  5  VB
 VA 
8
 Fy  0 VA  VB  VC  (8  8)  0
5m
1 
395
EJ
(1)
Pbx 2
(  b 2  x 2 )
6EJ
 1 5  3 2 2 2
C X1  6  8  EJ (8  5  3 )
 1 9,375
(2)
X1 
EJ
Na tabela: y 
A
B
3m
1
5m
Equação de Compatibilidade: 1  VB X1  0
395
 9,375
 VB
 0  VB  9,375  395  VB  42,133 kN
EJ
EJ
Com as equações de equilíbrio temos que: VA  5,667 kN e VC  16,200 kN
1  VBX1 
Engenharia Civil
1
profwillian.com
Lista de Exercícios
Método das Forças
2 – Trace os digramas de esforços solicitantes da viga contínua abaixo:
5 kN
8 kN/m
A
B
3,0m
C
2,5m
4,5m
VA
VB
VC
8 kN/m
C
8  5,5
[10 3  2  10  5,5 2  5,53 ]
24  EJ
1029,1875
q 
EJ
C
p 
5  3  4,5
[10 2  3 2  4,5 2 ]
6  10  EJ
p 
79,59375
EJ
1 
 1  4,5  5,5 2
[10  4,5 2  5,5 2 ]
6  10  EJ
1 
- 20,41875
EJ
q 
q
A
3,0m
2,5m
4,5m
5 kN
p
A
3,0m
2,5m
y
4,5m
Pbx 2
(  b 2  x 2 )
6EJ
1
A
3,0m
C
2,5m
4,5m
1
( q   p )  VB  1  0  VB  
VA  19,064 kN
e
( q   p )
1
 VB  
VC  11,634 kN
Diagrama de Momentos Fletores
Diagrama de Cortantes
-+19,064
2,383 m
(1029,1875  79,59375)
 VB  54,302 kN
 20,41875
-28,648
+24,366
2,383 m
3,046 m
3,046 m
-11,634
8,459
-29,936
22,714
Engenharia Civil
2
profwillian.com
Lista de Exercícios
Método das Forças
3 - Calcule as reações de apoio do pórtico hiperestático representado pela figura abaixo. Considere
todas as barras de mesma inércia EI e trabalhando fundamentalmente à flexão. A barra 1 tem 3 m e
a barra 2 tem 5 m. As equações de momentos fletores são fornecidas para a redundante de primeiro
gênero, apoio na extremidade da barra 3, que tem 1,5 m de comprimento.
0,6 kN/m
2
3
1,2 kN
1
0,6 kN/m
2
x
2
x
3
3
x
1
M1 ( x )  1,2 x  9,3
x
1
M2 (x)  x
1
0
M 2 ( x )  0,3x 2  1,8
M 3 ( x )  1,2 x
x
M1 ( x )  5
1,2 kN
M3 (x)  0
x
1
Solução:
3
5
EI  0   (1,2x  9,3)(5)dx   (0,3x 2  1,8)( x )dx  112,5  24,375  136,875
0
0
3
5
0
0
EI 1   (5)(5)dx   ( x )( x )dx  75  41,6667  116,6667
 136,875

EI
Equação de compatibilidade:  0  VB 1  0  VB   0  
 1,173 kN
116,6667
1
EI
Resposta:
 VB  1,173 kN
Através das equações de equilíbrio estático temos:
 F  0  H  1,2 kN
 F  0  V  1,827 kN
 M  0  M  3,435 kN.m
x
A
y
A
z
Engenharia Civil
VB
HA
VA
MA
A
3
profwillian.com
Lista de Exercícios
Método das Forças
4 - Utilize o Método das Forças para calcular as reações de apoio do quadro hiperestático representado pela figura
abaixo. As barras AC e BD possuem inércia à flexão EI e a barra CD tem inércia 2EI. Considere todas as barras
trabalhando fundamentalmente à flexão.
D
C
2m
8 kN
B
2m
A
HA
MA
VB
VA
6m
Solução:
Escolhendo VB como redundante:
D
C
2m
8 kN
∑
∑
∑
B
2m
A
HA



MA
VA
6m
Equações de esforços de cada uma das barras para o carregamento original.
Mx
Mx
Nx
Nx
Vx
Vx
Barra AC
D
x
B
16
A
Nx
Vx
x
8
Mx
x
8 kN
B
8 kN
Barra CD
Barra BD
∑
∑

∑


Equações de esforços de cada uma das barras para a carga unitária.
Retornando uma carga unitária no lugar de VB:
D
C
2m
B
2m
HA
VA
Engenharia Civil
1
A
MA
∑
∑
∑



6m
4
profwillian.com
Lista de Exercícios
Método das Forças
Equações de esforços de cada uma das barras para o carregamento original.
Barra AC
Barra BD
Mx
Mx
Nx
Nx
Vx
Vx
D
x
6
x
B
B
A
Barra CD
Nx
Vx
x
1
1
1
∑
Mx
∑

∑

Assim, o deslocamento devido ao carregamento original, 0, é:
∫
∫
Assim, o deslocamento devido a carga unitária, 1, é:
∫
∫
Portanto:
As demais reações são calculadas através das equações de equilíbrio estático:
D
C
2m
8 kN
B
2m
HA
VA
∑

∑

∑

A
MA
VB
6m
Resposta: As reações são (de acordo com os sentidos dos vetores vistos no desenho acima):
8,00 kN
HA=
0,80 kN
VA=
20,80 kN.m
MA=
-0,80 kN
VB=
Engenharia Civil
5
profwillian.com
Lista de Exercícios
Método das Forças
5 - Calcule a reação de apoio em B do pórtico hiperestático representado pela figura abaixo.
Considere a barra 1 de inércia EI e a barra 2 de inércia 8EI, todas trabalhando fundamentalmente à
flexão. Considere q = 10 kN/m.
q
C
B
2
2,5 m
VB
1
A
5m
Solução:
Equações de momentos fletores pra carregamento original e carregamento unitário:
q
0
2
x
1
x
M1 ( x )  125
M 2 ( x )  5 x 2
1
x
2
x
1
1
M1 (x )  5
M 2 (x)  x
(125)(5)
(5x 2 )( x )
 1660,16
dx

0 EI
0 8EI dx  EI
2,5
0 
2,5
1 
5
5
(5)(5)
( x )( x )
67,7083
0 EI dx  0 8EI dx  EI
 1660,16

EI
Equação de compatibilidade:  0  VB 1  0  VB   0  VB  
67,7083
1
EI
Resposta: VB  24,5192 kN
Engenharia Civil
6
profwillian.com
Lista de Exercícios
Método das Forças
6 - Através do Método das Forças, calcular as reações de apoio do pórtico da questão 1. Substitua o
apoio B por uma mola (na direção vertical) com constante de mola k = 8×103 kN/m, módulo de
elasticidade longitudinal E = 2×108 kN/m2 e momento de inércia I = 8×10-5 m4.
 0  VB 1  
0
VB
 VB  
1
k
 1
k
Solução:
Deslocamento vertical de B devido ao carregamento original:
0 
 1660,16
 1660,16

 0,10376
EI
2  108  8  10 -5
Deslocamento vertical do nó 4 devido ao carregamento unitário:
67,7083
67,7083

 0,0042318
EI
2  108  8  10 -5
1 
Equação de compatibilidade: a soma dos deslocamentos deve ser o deslocamento do nó 4 com a
mola.
0
V
 0,10376
 0  VB 1   B  VB  

 23,8158 kN
1
1
k
 1
 0,0042318
k
8000
Resposta:
q
 VB  23,8158 kN
C
2
B
Através das equações de equilíbrio estático temos:
 F  0  H  0 kN
 M  0  M  5,921 kN.m
 F  0  V  26,1842 kN
x
1
A
z
y
A
HA
A
A
VA
Engenharia Civil
VB
7
MA
profwillian.com
Lista de Exercícios
Método das Forças
7 - Através do Método das Forças, calcular a reação de apoio do nó 4 da treliça abaixo. Considere
os nós como rótulas perfeitas. Todas as barras têm inércia EA. A redundante escolhida foi a reação
vertical do nó 4. Note que os esforços normais nas barras foram fornecidos. As barras são
identificadas pelos seus nós iniciais Ni e nós finais Nf. Na tabela abaixo: N0 são os esforços nas
barras para os carregamentos originais e N1 são os esforços para uma força unitária para cima
aplicada no nó 4.
3 kN
6
7
1,5 m
5
4 kN
1
2
2m
3
2m
4
2m
V4
Solução:
Ni Nf
1 2
2 3
3 4
5 6
6 7
1 5
2 6
3 7
2 5
3 6
4 7
N0
-14,66667
-5,33333
0,00000
5,33333
0,00000
0,00000
-7,00000
-4,00000
11,66667
6,66667
0,00000
N1
4,00000
2,66667
1,33333
-2,66667
-1,33333
0,00000
1,00000
1,00000
-1,66667
-1,66667
-1,66667
L
2,0
2,0
2,0
2,0
2,0
1,5
1,5
1,5
2,5
2,5
2,5
N0× N1×L
-117,333
-28,444
0,000
-28,444
0,000
0,000
-10,500
-6,000
-48,611
-27,778
0,000
-267,111
Ni Nf
1 2
2 3
3 4
5 6
6 7
1 5
2 6
3 7
2 5
3 6
4 7
N1
4,00000
2,66667
1,33333
-2,66667
-1,33333
0,00000
1,00000
1,00000
-1,66667
-1,66667
-1,66667
N1
4,00000
2,66667
1,33333
-2,66667
-1,33333
0,00000
1,00000
1,00000
-1,66667
-1,66667
-1,66667
L
2,0
2,0
2,0
2,0
2,0
1,5
1,5
1,5
2,5
2,5
2,5
N0× N1×L
32,000
14,222
3,556
14,222
3,556
0,000
1,500
1,500
6,944
6,944
6,944
91,389
Deslocamento vertical do nó 4 devido ao
carregamento original:
0 
N
0
N1 L
EA

- 267,111
EA
Deslocamento vertical do nó 4 devido ao
carregamento unitário:
1 
 N N L  91,389
1
EA
1
EA
Equação de compatibilidade: a soma dos deslocamentos deve ser o deslocamento do nó 4 com o
apoio, ou seja, igual a zero.
- 267,111
0
 0  V4 1  0  V4  
  EA
 2,923 kN
91,389
1
EA
Resposta: A reação de apoio do nó 4 é de 2,923 kN.
Engenharia Civil
8
profwillian.com
Lista de Exercícios
Método das Forças
8 - Através do Método das Forças, calcular as reações de apoio da treliça da questão 2. Retire o
carregamento original e aplique um aumento uniforme de temperatura de 8ºC nas barras do banzo
superior (barras 5-6 e 6-7), sendo que a área A = 8×10-4 m2, módulo de elasticidade longitudinal
E = 2×108 kN/m2 e coeficiente de dilatação térmica =1,2×10-5 ºC-1.
 0    L T N
Solução:
Deslocamento vertical do nó 4 devido ao carregamento unitário:
 N N L  91,389 
1 
1
1
EA
EA
91,389
 5,7118  10 -4
8
-4
2  10  8  10
Deslocamento vertical do nó 4 devido ao aumento uniforme de temperatura na barra 2-4:
Ni Nf
5
6
6
7

0,000012
0,000012
L
T
2,0
2,0
8
8
 L T N1
N1
-2,66667
-1,33333
-0,000512
-0,000256
-0,000768
 0    L T N  0,000768
Equação de compatibilidade: a soma dos deslocamentos deve ser o deslocamento do nó 4 com o
apoio, ou seja, igual a zero.

 0,000768
 0  V4 1  0  V4   0  
 1,3446 kN
1
5,7118  10 -4
Resposta:
 V4  1,3446 kN
H5
V5
6
7
Através das equações de equilíbrio
estático temos:
M  0 
F  0  H
F  0  V
H 1  5,378 kN
z (5)
x
5
 5,378 kN
y
5
 1,3446 kN
Engenharia Civil
H1
1
2
3
V4
9
profwillian.com
Lista de Exercícios
Método das Forças
9 - Através do Método das Forças, calcular a reação de apoio do nó 3 da treliça abaixo. Considere
os nós como rótulas perfeitas. As diagonais têm inércia EA e os banzos têm inércia 4EA. A
redundante escolhida foi a reação vertical do nó 3. Note que os esforços normais nas barras foram
fornecidos. As barras são identificadas pelos seus nós iniciais Ni e nós finais Nf. Na tabela abaixo:
N0 são os esforços nas barras para os carregamentos originais e N1 são os esforços para uma força
unitária para cima aplicada no nó 3. A altura da viga é de 1 m (distância entre os banzos inferiores e
superior).
1 kN
1m
2 kN
1m
1m
2
1m
Ni
1
2
3
4
1
3
2
4
1
3
Nf
2
3
4
5
3
5
4
N0
-1,7678
0,3536
-0,3536
-2,4749
1,2500
1,7500
-1,5000
N1
0,7071
-0,7071
-0,7071
0,7071
-0,5000
-0,5000
1,0000
5
Solução:
Deslocamento vertical do nó 3 devido ao carregamento original:
Ni Nf
N0
N1
L
N0.N1.L EA N0.N1.L/EA
1
2
-1,7678
0,7071 1,41 -1,7678
1
-1,7678
2
3
0,3536 -0,7071 1,41 -0,3536
1
-0,3536
3
4
-0,3536 -0,7071 1,41 0,3536
1
0,3536
4
5
-2,4749
0,7071 1,41 -2,4749
1
-2,4749
1
3
1,2500 -0,5000 2,00 -1,2500
4
-0,3125
3
5
1,7500 -0,5000 2,00 -1,7500
4
-0,4375
2
4
-1,5000
1,0000 2,00 -3,0000
4
-0,7500
=
-5,7427
0 
N
0
N1 L
EA

- 5,7427
EA
Deslocamento vertical do nó 3 devido ao carregamento unitário:
Ni Nf
N1
N1
L
N1.N1.L EA N1.N1.L/EA
1
2
0,7071
0,7071 1,41 0,7071
1
0,7071
2
3
-0,7071 -0,7071 1,41 0,7071
1
0,7071
3
4
-0,7071 -0,7071 1,41 0,7071
1
0,7071
4
5
0,7071
0,7071 1,41 0,7071
1
0,7071
1
3
-0,5000 -0,5000 2,00 0,5000
4
0,1250
3
5
-0,5000 -0,5000 2,00 0,5000
4
0,1250
2
4
1,0000
1,0000 2,00 2,0000
4
0,5000
=
3,5785
1 
 N N L  3,5785
1
EA
1
EA
Equação de compatibilidade: a soma dos deslocamentos deve ser o deslocamento do nó 3 com o
apoio, ou seja, igual a zero.
- 5,7427

 0  V3 1  0  V3   0   EA  1,605 kN
3,5785
1
EA
Resposta: A reação de apoio do nó 3 é de 1,605 kN.
Engenharia Civil
10
profwillian.com
Lista de Exercícios
Método das Forças
10 - Através do Método das Forças, calcular as reações de apoio da treliça da questão 2 em apenas
um dos dois casos seguintes:
a) retire o carregamento original e aplique um aumento uniforme de temperatura de 20ºC na barra
2-4, sendo que A = 0,02 m2, E = 2×108 kN/m2 e =10-5 ºC-1.
Solução:
Deslocamento vertical do nó 3 devido ao carregamento unitário:
1 
 N N L  3,5785 
1
1
EA
EA
3,5785
 8,95  10 -7
8
2  10  0,02
Deslocamento vertical do nó 3 devido ao aumento uniforme de temperatura na barra 2-4:
 0   L T N 24  10 5  2,0  20  1,0  4  10 4 m
Equação de compatibilidade: a soma dos deslocamentos deve ser o deslocamento do nó 3 com o
apoio, ou seja, igual a zero.

4  10 4
 0  V3 1  0  V3   0  
 447,1 kN
1
8,95  10 -7
Resposta:
2
4
 V3  447,1 kN
Através das equações de equilíbrio estático temos:
 F  0  H  0 kN
 M  0  V  223,6 kN
 F  0  V  223,6 kN
x
H1
1
z
1
3
5
1
y
V3
V1
5
V5
b) substitua o apoio do nó 3 por uma mola com k = 2000 kN/m, A = 0,02 m2, E = 2×108 kN/m2.
Solução:
Deslocamento vertical do nó 3 devido ao carregamento original:
0 
N
0
N1L
EA

- 5,7427
- 5,7427

 1,436  10 -6 m
EA
2  10 8  0,02
Deslocamento vertical do nó 3 devido ao carregamento unitário:
1 
 N N L  3,5785 
1
1
EA
EA
3,5785
 8,946  10 -7
2  10 8  0,02
Equação de compatibilidade: a soma dos deslocamentos deve ser o deslocamento do nó 3 com a
mola.
V
0
 1,436  10 6
 0  V3 1   3  V3  

 0,00286 kN
1
1
k
-7
 1
 8,95  10
k
2000
Resposta:
1 kN
 V3  0,002866 kN
2
Através das equações de equilíbrio estático temos:
 F  0  H  0 kN
 M  0  V  1,248567 kN
 F  0  V  1,748567 kN
x
2 kN
4
1
z
y
Engenharia Civil
H1
1
1
3
5
V1
11
5
V3
V5
profwillian.com