estudo da variação da capacitância de capacitores

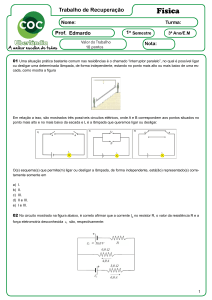
ESTUDO DA VARIAÇÃO DA CAPACITÂNCIA DE CAPACITORES COMERCIAIS
Carolina R. Ramos Pinto1, Rafael H. Mota de Siqueira2,4, Jose R. A. Guede3,
José O. Rossi4
1
UNIVAP/FEAU, São José dos Campos – SP, [email protected]
UNESP/Dep. Materiais e Tecnologia, Guaratinguetá – SP, [email protected]
3
UNIVAP/FEAU, São José dos Campos – SP, [email protected]
4
INPE/Lab. Associado de Plasma, São José dos Campos – SP, [email protected]
2
Resumo – Neste trabalho, pretende-se mostrar que a capacitância de capacitores comerciais com
dielétricos são dependentes da tensão aplicada e da taxa de repetição de carga e descarga. Os estudos
destas propriedades são de vital importância para o uso de capacitores cerâmicos em sistemas de
armazenamento de alta energia e nas aplicações não-lineares de redes LC para a geração de RF. Para isto,
são propostos dois circuitos para medição da capacitância em condições estáticas (variação da tensão
aplicada DC) ou dinâmicas (variação da frequência de carga e descarga do capacitor). Por último, alguns
resultados experimentais são mostrados neste artigo para ilustrar o estudo destas propriedades dos
materiais dielétricos cerâmicos.
Palavras-chave: Constante dielétrica; Capacitor; Materiais cerâmicos
Área do Conhecimento: Engenharia Elétrica; Propriedades de Materiais Elétricos
Introdução
A idéia de medir a capacitância de capacitores
comerciais em função da tensão aplicada está
relacionada com duas aplicações básicas em
engenharia de potência pulsada: redes LC
formadoras de pulso e redes LC não-lineares.
Na primeira aplicação, deseja-se produzir
pulsos retangulares para alimentar cargas lineares
numa certa taxa de repetição de pulso como na
alimentação de tubos para RF (klystrons ou
magnetrons). Neste caso, a linha LC formadora de
pulso casada a carga de saída é descarregada
para a produção do pulso com formato retangular.
E como a impedância característica da linha e o
tempo de propagação são dados respectivamente
por
L / C e n× LC (onde n é o número de
células LC) é óbvio que a dependência da
capacitância com a tensão ou a freqüência de
repetição implicaria na distorção do pulso de
saída. Por outro lado, na segunda aplicação há um
grande interesse em explorar este efeito não-linear
(WILSON et. al., 1991 – SMITH, 2002). Por
exemplo, em circuitos de compressão de pulso
para a produção de pulsos extremamente rápidos
(normalmente na faixa de ns) a variação de C com
V leva a uma redução do tempo de subida do
pulso na saída, uma vez que a velocidade de
propagação é inversamente proporcional a raiz
quadrada de LC, isto é
LC(V ) . Para um pulso
se obter um pulso de saída mais rápido a partir de
um pulso mais lento injetado na entrada de uma
rede LC. Circuitos de compressão operam
normalmente em modo disparo único ou com
baixa taxa de repetição (algumas dezenas de Hz),
porém com o aumento da freqüência espera-se
uma redução do valor da capacitância em função
do aumento de temperatura e de perdas do
dielétrico. Para aplicações lineares, geralmente
utilizam-se capacitores contendo dielétricos de
mica ou plásticos (poliéster, polipropileno, etc) que
são mais estáveis em termos de capacitância
(STRYDOM et. al., 1999). Já para aplicações nãolineares capacitores cerâmicos são mais usados
porque cerâmicas a base de titanato de bário ou
estrôncio deixam de ser materiais ferroelétricos
lineares acima da Temperatura de Courier (sendo
conhecidos nesta fase como paraelétricos).
O objetivo desta proposta é o de medir a
capacitância de diversos capacitores comerciais
em função da tensão aplicada ou da frequência de
repetição de pulso com a finalidade de estudar
melhor a aplicabilidade destes dispositivos tanto
em circuitos lineares como não-lineares.
Metodologia
Para os estudos foram comprados três
capacitores cerâmicos de diferentes fabricantes,
segue abaixo os valores comerciais dos
componentes na Tab. 1.
propagando nesta rede não-linear, o pico de
tensão chega à saída antes que as partes iniciais
de mais baixa amplitude do pulso, comprimindo o
mesmo através da redução do seu tempo de
subida. Portanto, esta é uma excelente maneira de
XIII Encontro Latino Americano de Iniciação Científica e
IX Encontro Latino Americano de Pós-Graduação – Universidade do Vale do Paraíba
1
Tabela 1 - Características e dimensões dos
capacitores utilizados.
Capacitores
Voltagem
(kV)
Fabricante
1
Fabricante
2
Fabricante
3
Capacitância
(nF)
Diâmetro
(mm)
Espessura
(mm)
3,0
2,0
15
1,5
2,0
10
12
1,0
1,0
4,7
7,5
0,5
Na segunda aplicação, onde se deve medir a
dependência de C com a taxa de repetição numa
determinada tensão de carga V. Neste caso, uma
fonte DC carrega o dispositivo sob teste (C2) via
resistores R1 e R2 e a chave de estado sólido
IGBT descarrega o capacitor em cada ciclo de
repetição como mostrado na Fig. 2.
R1
2Meg
L1
0.1uH
L3
0.1uH
L2
0.1uH
+
Primeiramente foram executados os testes
elétricos para a medição das capacitâncias. Os
testes foram feitos em duas partes, no circuito 1
pretende-se medir a capacitância (C) variando a
tensão DC aplicada V entre os terminais do
capacitor, já no circuito 2 aspira-se obter valores
para a capacitância (C) com a freqüência de
repetição de pulso numa determinada tensão de
carga V.
Na execução do circuito 1 foi utilizada uma
fonte DC de alta tensão (AT), que polariza o
capacitor sob teste. Para isolar o potencial de AT
da fonte DC, foi colocada uma ponte em série com
capacitores lineares de 1µF-400 V. Portanto com a
ponte obteve-se um valor final para C2=200 nF , o
que é uma alta capacitância para proteger a
entrada do capacímetro, já os dois resistores de
10 MΩ são utilizados para carga e descarga de
ambos capacitores conforme a Fig. 1.
Com o mesmo circuito foram executados os
ensaios com os três capacitores cerâmicos não
lineares (C1).
C2
R1
10M
+
Vs1
1200v
R2
10M
C1
-
Figura 1 - circuito utilizado para o primeiro teste.
R2
Vs1
800V
-
100k
R3
1
C2
1nF
V1
0/15V
100 Hz
R5
47
Q1
IRGB420U
D3
1N5248B
D2
1N4007
R4
1
C1
10nF
D1
1N4007
Figura 2 - Circuito utilizado para o segundo teste.
Para a implementação do circuito 2 foi utilizado
uma fonte DC de alta tensão 1000 V, cinco
resistores (R1=2 MΩ; R2=100 kΩ; R3=47 Ω; R4=1
Ω; R5=1 Ω), dois capacitores, C2=1 nF e o
capacitor sob teste C1 do Fabricante 2 de 10 nF.
Na saída do gerador de pulsos (5 V – 100 Hz)
foram conectados um diodo zenner (1N5248B) e
um diodo (1N4007) na base do transistor IGBT
(IRGB42OU) para proteger a saída do gerador de
pulsos de baixa tensão. Para a proteção do
transistor contra transientes, um circuito snubber
do tipo RCD foi colocado entre coletor e emissor.
Para efeito de comparação com resultados
experimentais, foi feita uma simulação num
simulador SPICE para verificar a tensão de carga
e descarga no capacitor sob teste. O programa
SPICE utilizado foi o circuitMaker2000 o
circuitMaker
é
um
software
(simulador)
relativamente fácil de usar,com interface gráfica
para captura de diagramas esquemáticos de
eletrônica e uma ferramenta de simulação. A
forma de onda de voltagem do capacitor obtida na
simulação, com tensão DC da ordem de 800V e
com taxa de repetição de 100 Hz, encontra-se
mostrada na Fig. 3 abaixo.
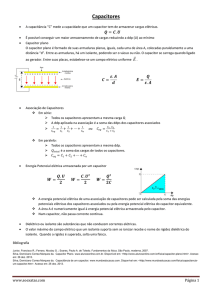
As curvas das constantes dielétricas relativas
foram obtidas na prática. Através da fórmula da
capacitância C = (ε A)/d (BARSOUM, 2003) , onde
C é o valor das capacitância medida para C1 na
Fig.1 e A e d são respectivamente a área
transversal e a espessura da cerâmica dielétrica
dos capacitores, encontra-se ε, que é a constante
dielétrica do material. Com ε e com o auxílio da
equação da constante dielétrica relativa k = ε/ ε0
(BARSOUM, 2003) onde ε0 é a constante dielétrica
-12
F/m)), determina-se as
no vácuo (8,85 X 10
constantes dielétricas relativas da cerâmica.
XIII Encontro Latino Americano de Iniciação Científica e
IX Encontro Latino Americano de Pós-Graduação – Universidade do Vale do Paraíba
2
Figura 3 – Simulação SPICE da tensão do
capacitor C1 sob teste em condições dinâmicas.
Analisando a forma de onda da tensão do
capacitor, pode-se calcular a capacitância de C1
tanto na carga como na descarga. Fazendo-se
uma aproximação linear durante o tempo de carga
do capacitor, pode-se calcular a capacitância na
carga em função da variação da tensão nos
terminais do capacitor ∆V e do tempo de carga tC
como:
Cc (V , t ) ≈
VDC t c
∆VRc
(1)
onde VDC é a tensão DC da fonte e Rc=R1 é o
resistor de carga (STRYDOM et. al., 1999). Por
outro lado, a capacitância na descarga, pode ser
calculada pelo decréscimo exponencial da
voltagem do capacitor ∆V durante o tempo de
descarga td como:
C d (V , t ) ≅
td
R d ln( ∆ V )
(2)
onde Rd=R2 é o resistor de descarga (STRYDOM
et. al., 1999). Se calcularmos as capacitâncias
levando em consideração as características da
Fig. 3 usando (1) & (2), temos respectivamente
uma capacitância de carga da ordem de 13 nF e
uma capacitância de descarga da ordem de 10 nF,
como esperado neste último caso, uma vez que a
capacitância C1 é fixa na simulação. Para o
primeiro caso, no caso da carga, a discrepância
maior do valor calculado deve-se ao fato de que a
Eq. (1) é uma aproximação matemática bastante
grosseira. Já no caso de (2), a aproximação é
muito mais precisa. Usando osciloscópio e um
termopar Tipo K (Cromel / Alumel) engastado no
corpo do capacitor sob teste, obtém-se
respectivamente as constantes de tempo para a
carga e descarga RC, a partir da forma de onda de
tensão do capacitor, e a temperatura do
componente a fim de determinar o efeito das
condições
dinâmicas
em
freqüência
na
capacitância do componente. Caso a operação em
frequência do componente aumente a temperatura
do dielétrico do capacitor, a forma de onda de
carga & descarga RC da voltagem do capacitor irá
se alterar, indicando que houve variação da
capacitância do dispositivo e, por conseguinte, da
constante dielétrica do material dielétrico do
componente.
Por último foi realizado uma microanálise da
composição química do dielétrico dos três
fabricantes, no microscópio eletrônico de
varredura (MEV - Jeol modelo JSM 5310)
equipado com detectores de energia dispersiva de
raios X (EDS). A preparação dos capacitores para
a análise em EDS consistiu em seccioná-los nos
diâmetros médios e lixados em lixas de carbeto de
silício, partindo de uma lixa com granulação
grossa para uma fina. Após o lixamento, as
amostras foram limpas em banho ultrassônico com
álcool isopropílico por 15 minutos.
Resultados & Discussões
Nos testes da Fig.1, obteve-se a curva da
capacitância versus a tensão (C×V) em linha
sólida para cada capacitor da Tab. 1, conforme os
resultados das Figs. 4, 5 & 6. Usando as
dimensões de cada capacitor dadas na Tab. 1,
calcula-se a correspondente constante dielétrica ε
para cada tensão aplicada e a correspondente
constante dielétrica k relativa a partir de ε/ε0, onde
as correspondentes curvas C×ε para os mesmos
capacitores
são mostradas
pelas
curvas
tracejadas nas Figs. 4, 5 & 6. Observe que as
formas das curvas C×ε são bastante similares às
de C×V como esperado. A partir disto, pode-se
analisar o comportamento de cada componente
com a variação da tensão aplicada. Normalmente,
para capacitores com dielétricos cerâmicos
espera-se uma diminuição da capacitância com o
aumento da tensão, conforme ilustrado pelo
gráfico da Fig. 6 para o capacitor do fabricante 3,
em função da saturação do alinhamento dos
dipolos a partir de um determinado valor de campo
elétrico. Dependendo do composto cerâmico do
dielétrico, às vezes ocorre um aumento da
capacitância no início para valores maiores de
tensão, tendo em vista que os dipolos apresentam
um comportamento linear em baixa tensão. Assim
que ocorre um alinhamento total, ocorre a
saturação e C decai com a tensão aplicada. Este
efeito é claramente mostrado pelo capacitor do
fabricante 2 na Fig. 5. Entretanto, no caso da Fig.
4, observamos apenas o aumento da capacitância
em função da tensão, pois a tensão máxima do
componente do fabricante 1 é de 3 kV e a máxima
tensão aplicada foi aproximadamente de 1 kV por
limitação da fonte de tensão DC, impedindo uma
medida completa do componente em sua inteira
utilização. Portanto, nesta situação ocorreu
apenas o alinhamento inicial dos dipolos do
dielétrico em sua faixa linear não atingindo o ponto
de saturação.
XIII Encontro Latino Americano de Iniciação Científica e
IX Encontro Latino Americano de Pós-Graduação – Universidade do Vale do Paraíba
3
Figura 4 - Capacitância versos tensão e constante
dielétrica fabricante 1.
Figura 5 - Capacitância versos tensão e constante
dielétrica fabricante 2.
Figura 6 - Capacitância versos tensão e constante
dielétrica fabricante 3.
Quanto aos testes dinâmicos da Fig. 2,
observou-se a seguinte forma de onda da tensão,
ilustrada na Fig. 7, para o capacitor do fabricante 2
de 10 nF-2 kV com as mesmas condições da
simulação (tensão da fonte da ordem de 800 V
com taxa de repetição de 100 Hz). Esta tensão foi
armazenada num osciloscópio digital Tektronix de
100 MHz e transferida para um PC. Observe que
há uma boa concordância da curva da Fig. 7 com
o resultado da simulação SPICE na Fig. 3. Após
um determinado tempo de 30 minutos, verificou-se
no osciloscópio que não havia alteração das
formas de ondas de carga & descarga RC,
indicando que não houve variação da capacitância
ou da constante dielétrica. Isto foi confirmado pela
medida de temperatura, dada pelo termopar ligado
ao corpo do componente, que permaneceu
inalterada na faixa de 20°C. Uma das razões para
esta estabilização da temperatura do dielétrico
com o capacitor em operação está ligada à baixa
taxa de repetição e a elevada tensão nominal do
capacitor que é muito superior ao pico de carga da
ordem de 130 V.
Figura 7. Tensão de carga & descarga do
capacitor do fabricante 2 sob teste em freqüência.
As análises de EDS das Figs. 8, 9 & 10
forneceram espectros da composição química das
cerâmicas dielétricas para os respectivos
capacitores dos fabricantes 1, 2 & 3. O dielétrico
do Fabricante 1 (Fig. 8) é composto de carbono
(C), titânio (Ti), estrôncio (Sr), chumbo (Pb), cálcio
(Ca) e bário (Ba) e os dielétricos dos Fabricantes 2
(Fig. 9) e 3 (Fig. 10) são compostos de titânio (Ti),
estrôncio (Sr), cálcio (Ca) e bário (Ba). A partir dos
resultados de EDS estima-se que os dielétricos
possam ser de titanato de bário (BaTiO3), ou
titanato de estrôncio (SrTiO) e ou um compósito
de titanato de bário e estrôncio (BaxSr1-xTiO3).
Como as cerâmicas estudadas apresentaram
constantes dielétricas extremamente elevadas,
pode-se inferir que se trata de um dos compostos
acima citados. Esta propriedade apresentada
pelas
cerâmicas
comerciais
as
torna
especialmente úteis para algumas aplicações em
capacitores (CALLISTER, 2000). O elemento
chumbo (Pb) encontrado no dielétrico do
Fabricante 1, na forma de óxido de chumbo
(litargírio – PbO), melhora as propriedades
XIII Encontro Latino Americano de Iniciação Científica e
IX Encontro Latino Americano de Pós-Graduação – Universidade do Vale do Paraíba
4
dielétricas do bário (ICZ, 2009). Já os elementos
carbono (C), encontrado na cerâmica do
Fabricante 1, e cálcio (Ca), encontrado no
dielétrico nos três fabricantes, são impurezas
presentes nos óxidos.
Figura 8 - EDS da cerâmica dielétrica do capacitor
do Fabricante 1.
Figura 9 - EDS da cerâmica dielétrica do capacitor
do Fabricante 2.
Os resultados mostraram que sob condições
estáticas há um decréscimo da constante
dielétrica de capacitores cerâmicos com o
incremento da tensão (CxV). Estes resultados são
de suma importância no projeto de circuitos que
utilizam tais tipos de capacitores, nos quais não se
espera que haja variação da capacitância com a
tensão aplicada. Já para aplicações não-lineares,
estes dados podem contribuir para o projeto de
redes LC que utilizam tais capacitores nãolineares, uma vez que para cada capacitor a curva
CxV pode ser traçada. Já os testes sob condições
dinâmicas, os resultados ainda não foram
conclusivos, já que não houve aumento da
temperatura do dielétrico por causa da baixa taxa
de repetição. Além disto, sabemos que com o
aumento da temperatura materiais dielétricos
cerâmicos tem sua constante dielétrica bastante
aumentada até a temperatura de Curie, cujo ponto
além do qual ocorre um decréscimo grande da
constante
com
sucessivo
incremento
da
temperatura. Portanto, para o futuro já se está
planejando aumentar a freqüência dos testes
dinâmicos para verificar esta dependência da
constante dielétrica com a temperatura. Para isto,
no circuito de testes da Fig. 2, os resistores de
carga e descarga devem ser redimensionados
para valores menores, porém com maior potência
de dissipação.
Quanto à composição química dos dielétricos
analisados verifica-se que ela é basicamente a
mesma (Ti, O, Ba, Sr) para todos os três
componentes e que estas cerâmicas apresentam
constantes dielétricas elevadas, sendo ideal para
a manufatura de capacitores. A adição de alguns
elementos a composição básica dos dielétricos,
como o chumbo (Pb) do Fabricante 1, são
individualidades de cada fabricante conferindo
características próprias ao produto.
Agradecimentos
Agradecemos ao Instituto Nacional de
Pesquisas Espaciais (INPE) – Centro de
Tecnologias
Especiais
(CTE)/Laboratório
Associado de Plasma (LAP), ao Ministério de
Ciências e Tecnologia (MCT) e a Universidade do
Vale do Paraíba (UNIVAP).
Referências
Figura 10 - EDS da cerâmica dielétrica do
capacitor do Fabricante 3.
- WILSON, C.R.; TURNER, M.M.; and SMITH,
P.W. “Pulse Sharpening in a Uniform LC Ladder
Network Containing Nonlinear Ferroelectric
Capacitors,” IEEE Trans. Electron Dev., vol. 38,
1991, pp. 767- 771.
Conclusões
XIII Encontro Latino Americano de Iniciação Científica e
IX Encontro Latino Americano de Pós-Graduação – Universidade do Vale do Paraíba
5
- SMITH, P.W. Transient Electronics – Pulsed
Circuit Technology, West Sussex, England: John
Wiley & Sons, 2002, pp. 245-249.
- STRYDOM, J.T.; VAN WYK, J.D.; and
FERREIRA, J.A. “Capacitor Measurements for
Power Electronic Applications,” in Proc. of the
IEEE Industry Applications Conference, 1999, pp.
2435- 2440.
- BARSOUM, M.W. Fundamentals of ceramics.
2. ed. Philadelphia: IOP, 2003. 603 p.
- CALLISTER, W.D. Ciência e engenharia de
materiais: Uma introdução. 5. ed. Rio de
Janeiro: LTC, 2000. 589 p.
- ICZ (Instituto de metais não ferrosos). Disponível
em: <http://www.icz.org.br/chumbo-industria.php>.
Acesso em 03 de setembro 2009.
XIII Encontro Latino Americano de Iniciação Científica e
IX Encontro Latino Americano de Pós-Graduação – Universidade do Vale do Paraíba
6