Apoio didático para o Ensaio 1

Apoio didático para o Ensaio 1
1. Carga linear [1]
Quando uma onda de tensão alternada senoidal é aplicada aos terminais de uma carga
linear, a corrente que passa pela carga também é uma onda senoidal. Exemplos de
cargas lineares: resistores, indutores e capacitores.
2. Fasor [1]
2.1. O que é?
É um número complexo que representa o valor eficaz e a fase de uma senoide.
2.2. Definição de valor eficaz e fase
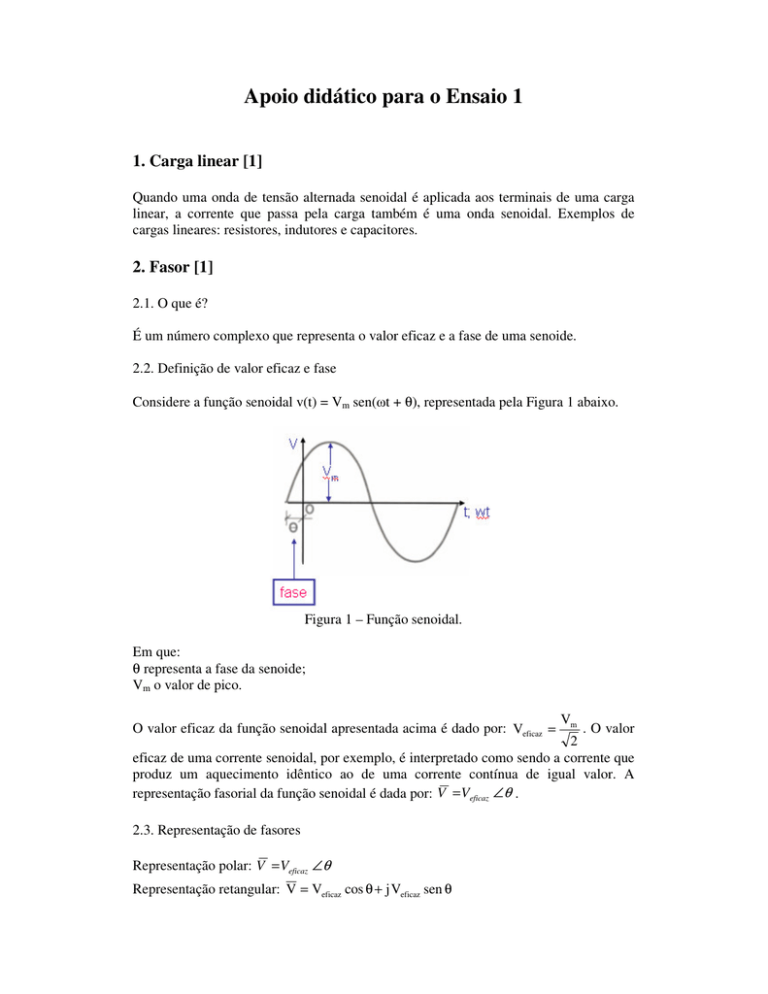
Considere a função senoidal v(t) = Vm sen(ωt + θ), representada pela Figura 1 abaixo.
Figura 1 – Função senoidal.
Em que:
θ representa a fase da senoide;
Vm o valor de pico.
O valor eficaz da função senoidal apresentada acima é dado por: Veficaz =
Vm
. O valor
2
eficaz de uma corrente senoidal, por exemplo, é interpretado como sendo a corrente que
produz um aquecimento idêntico ao de uma corrente contínua de igual valor. A
representação fasorial da função senoidal é dada por: V = Veficaz ∠θ .
2.3. Representação de fasores
Representação polar: V = Veficaz ∠θ
Representação retangular: V = Veficaz cos θ + j Veficaz sen θ
2.4. Quando usar?
a) o circuito for linear;
b) a resposta em regime permanente for alcançada;
c) todas as fontes independentes forem senoidais e possuírem a mesma freqüência.
3. Potências [1]
Considere os seguintes fasores de tensão e corrente:
V = V ∠θ
e
I = I ∠β
A potência complexa que flui nos circuitos elétricos é definida como sendo:
S = V I*
Na forma polar, tem-se que a potência aparente é dada por:
S = V I ∠φ
Em que φ = θ − β
Na forma retangular, tem-se que a potência aparente é dada por:
S = V I cos φ + j V I senφ
A parte real de S, conhecida como potência ativa, V I cos φ, é aquela que efetivamente
produz trabalho útil, gerando calor, luz, movimento, etc. Enquanto que a parte
imaginária de S, conhecida como potência reativa, V I sen φ, é aquela que circula
continuamente entre os diversos campos elétricos e magnéticos de um sistema de
corrente alternada sem produzir trabalho útil.
As unidades e símbolos das potências são dados por:
Potência
complexa
ativa
reativa
Tabela 1 – Potências.
Símbolo
Fórmula
S
S = V I*
P
P = V I cosφ
Q
Q = V I senφ
Unidade
VA
W
var
4. Instrumentos de medição [2]
4.1. Voltímetro
O voltímetro é um instrumento de medida da amplitude da tensão elétrica. Se a tensão
for senoidal, ele medirá o valor eficaz (valor rms) da tensão. É dotado de duas pontas de
prova e é sempre ligado em paralelo, conforme apresentado na Figura 2.
Figura 2 – Ligação do voltímetro.
4.2. Amperímetro
O amperímetro é um instrumento de medida da amplitude da corrente elétrica. Se a
corrente for senoidal, ele medirá o valor eficaz (valor rms) da corrente. É dotado de
duas pontas de prova e é sempre ligado em série, conforme apresentado na Figura 3.
Figura 3 – Ligação do amperímetro.
4.3. Wattímetro
O wattímetro é um instrumento que mede a potência elétrica consumida por um
elemento. O wattímetro realiza o produto das grandezas tensão e corrente elétrica no
elemento, razão pela qual a sua ligação ao circuito é feita simultaneamente em série e
em paralelo, ver Figura 4. Assim, dois dos terminais são ligados em paralelo com o
elemento, efetuando a medição da tensão, e os dois restantes são interpostos no caminho
da corrente.
Figura 4 – Ligação do wattímetro.
5. Comentários sobre a resistência de lâmpadas [3]
A resistência inicial da lâmpada de filamento de tungstênio (lâmpada atual comum) é
baixa. Conforme a temperatura aumenta (pelo aumento da corrente) a relação V/I
aumenta (a resistividade do tungstênio aumenta com a temperatura). Com a lâmpada de
filamento de carvão (lâmpada tipo Edson) o comportamento é oposto; a resistência
inicial (fria) é alta e diminui com o aquecimento (a resistividade do carvão diminui com
a temperatura).
6. Exercícios
6.1 Obtenha a soma de 3 correntes senoidais que chegam a um nó de um circuito,
expressas por:
i1 = 5 2 sen wt
i 2 = 6 2 sen ( wt + 30 o )
i 3 = 8 2 sen ( wt − 90 o )
Resp: 11,35 ∠ − 26,12 0 A ou i(t) = 16,05 sen(ωt – 26,120)
6.2 A tensão de uma linha CA de alimentação comercial é de 240V. Qual a tensão de
pico?
Resp: 339,41 V
6.3 Uma fonte de tensão de 13,8 kV, alimenta uma carga que consome 1000 kW e
possui cosφ igual a 0,9. Saiba que entre a geração e a carga existe uma linha de
transmissão cuja impedância resistiva é de 2Ω. Calcule:
A corrente que alimenta a carga: __________________
A capacidade da fonte em kVA: __________________
A perda na linha em kW: __________________
A queda de tensão na linha de transmissão: __________________
Resp: 80,51 A; 1111,03 kVA; 12,963 kW; 161,02V
7. Bibliografia
[1] Circuitos Polifásicos; Almeida e Damasceno Freitas, Finatec, 1995.
[2] http://www.colegiouberaba.com.br/apostilas/eletri/Corrente%20Cont%EDnua.pdf
[3] http://www.feiradeciencias.com.br/sala15/15_10.asp