grandesas elétricas

GRANDEZAS ELÉTRICAS
1.3 - CORRENTE ELÉTRICA
Corrente: E´o movimento ou fluxo de elétrons.
Para produzir corrente: Os elétrons devem se deslocar pelo efeito de uma
diferença de potencial (ddp).
Representação da corrente: Letra (I).
Unidade fundamental da corrente: Ampére (A).
1A  1
C
s
Onde: A = Ampére
C = Coulomb
s = segundo
Definição da corrente
I
Q
T
Onde: I = Corrente (A)
Q = Carga (C)
T = tempo (s)
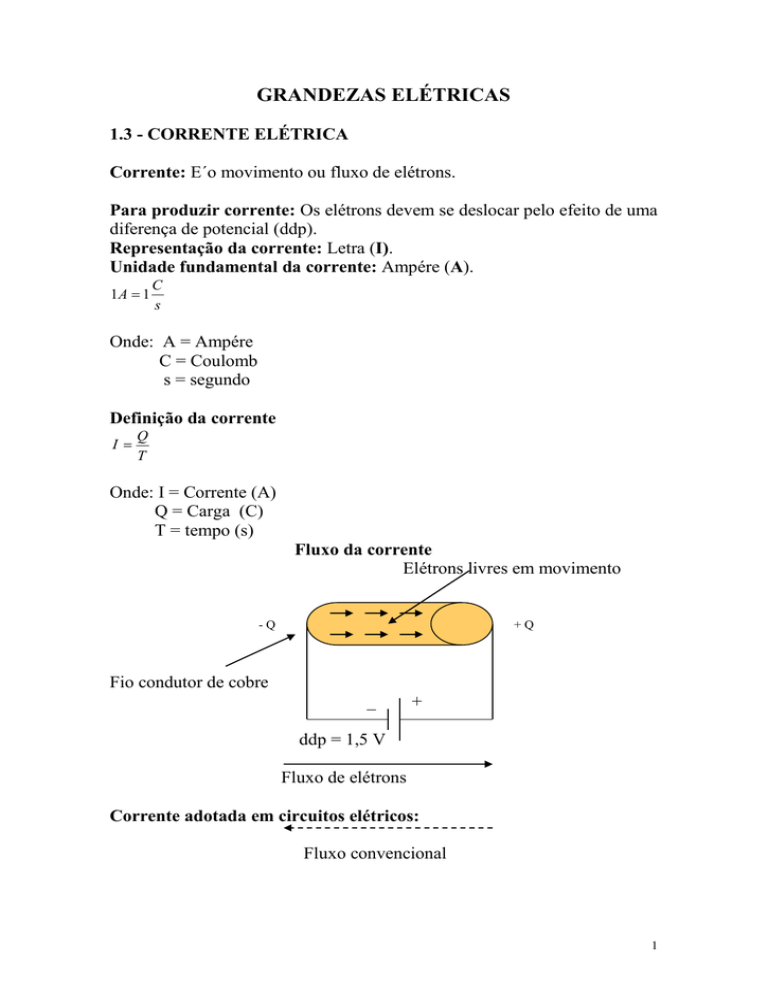
Fluxo da corrente
Elétrons livres em movimento
-Q
+Q
Fio condutor de cobre
_
+
ddp = 1,5 V
Fluxo de elétrons
Corrente adotada em circuitos elétricos:
Fluxo convencional
1
TIPOS DE CORRENTE
- Corrente contínua
- Corrente alternada
Aparelho utilizado para medir corrente: Amperímetro
Símbolo:
A
+
Como fazer a medição:
_
127 V
Amperímetro
Corrente contínua
I
+I
t
Obs.: A razão dessa corrente unidirecional se deve ao fato das fontes de tensão (pilhas,
baterias), manterem a mesma polaridade de tensão de saída.
Corrente alternada
I
+I
+
_
_I
t
Obs.: Em termos de fluxo convencional, a corrente flui do terminal positivo da fonte de
tensão, percorre o circuito e volta para o terminal negativo, mas quando o gerador
alterna a sua polaridade, a corrente tem que inverter o seu sentido.
2
AMPERÍMETRO DE PAINEL
MULTÍMETRO ANALÓGICO
3
MULTÍMETRO DIGITAL
4
ALICATE AMPERÍMETRO ANALÓGICO
5
Exercícios:
1) Se uma corrente de 2A passa através de um medidor durante 1 minuto,
quantos Coulombs passam pelo medidor?
Solução:
2) Calcule a corrente em ampéres quando uma carga de 650C passar
através de um fio em 50s.
3) Se 465C de carga passam através de um fio em 2,5minutos, qual será a
corrente em ampéres?
4) Se uma corrente de 40A é mantida por 1 min, quantos coulombs de
carga passam através do fio?
5) Quantos coulombs de carga passam através de uma lâmpada em 2 min se
a corrente for constante e igual a 750mA.
6) Se a corrente em um condutor for constante e igual a 2mA, quanto
tempo será necessário para 4.600x10-6 C passar através do condutor?
6
1.4 - TENSÃO ELÉTRICA
Tensão: E´a diferença de potencial, (ddp).
Unidade fundamental da tensão: Volt
Símbolo: V
A diferença de potencial V entre dois pontos é medida pelo trabalho
necessário à transferência de carga unitária de um ponto para o outro.
1V  1
J
C
Definição da tensão
V
W
Q
Onde:
- V = Tensão em Volts
- W = Energia em J
- Q = Carga em Coulomb (C)
Tipos de tensão
- Tensão em corrente contínua
- Tensão em corrente alternada
Aparelho utilizado para medir tensão: Voltímetro
Símbolo:
V
+
_
7
Como fazer a medição:
Voltímetro
127 V
Tensão de corrente alternada (VCA)
V
+V
+
_V
t
_
Uma fonte de tensão alternada inverte ou alterna periodicamente a sua
polaridade.
Tensão de corrente contínua (VCC)
V
+V
t
Uma fonte de tensão contínua pode variar o valor da sua tensão de saída,
mas se a polaridade for mantida, a corrente fluirá somente num sentido.
8
TERMINOLOGIA APLICADA A TENSÃO ELÉTRICA
Potencial: É a tensão num ponto em relação a outro ponto no sistema
elétrico. Normalmente o ponto de referência é o (ponto comum ou terra),
cujo potencial é igual a zero.
Exemplo:
3,3K
10K
2,2K
8V
4,7K
Voltímetro
Diferença de potencial (ddp): É a diferença algébrica de potencial (ou
tensão) entre dois pontos de um circuito.
Tensão: Quando esse termo aparece isolado, significa o mesmo que
potencial.
Diferença de tensão: É a diferença algébrica de tensão (ou potencial) entre
dois pontos de um sistema.
Exemplo: Queda ou aumento de tensão.
Força eletromotriz (fem): É a força que estabelece o fluxo de carga (ou de
corrente) em um sistema graças à aplicação de uma diferença de potencial.
Exemplo: Associado às fontes de energia elétrica.
9
VOLTÍMETRO DE PAINEL
10
FONTE DE ALIMENTAÇÃO DE CORRENTE CONTÍNUA
11
Exercícios:
1) Determine a diferença de potencial entre dois pontos de um sistema
elétrico, se 60J de energia forem gastos para deslocar uma carga de 20C
entre esses dois pontos.
2) Calcule o valor da carga Q que precisa de 96J de energia para ser
movida ao longo de uma diferença de potencial de 16 V.
3) Quanto de carga passa por uma bateria de 22,5V se a energia usada for
de 90J?
4) se a diferença de potencial entre dois pontos é 42 V, qual o trabalho
necessário para levar 6C de um ponto a outro?
12
1.5 – POTÊNCIA ELÉTRICA
Se um trabalho está sendo realizado em um sistema elétrico, uma
quantidade de energia está sendo consumida. E esta energia é chamada de
potência.
1W  1
P
J
s
W
t
Onde:
- P = potência (W)
- W = energia (J)
- t = tempo (s)
A variação da energia é dada pelo produto da tensão aplicada pela variação
da carga que se move através do elemento.
P  V .I
Onde:
- P = potência (W)
- V = tensão (V)
- I = corrente (A)
Aparelho utilizado para medir a potência: Watímetro
Símbolo:
W
13
Como fazer a medição:
- Forma direta
W
127V
Escala linear
Watts
Volts
Ampéres


Bobina fixa: Amperimétrica
Bobina móvel: Voltimétrica
- Forma indireta
A
127V
V
14
MEDIDOR DE kWh
15
ALICATE WATÍMETRO
16
Exercícios:
1) Se um resistor dissipa 429J em 7 min, qual a potência dissipada?
2) A potência dissipada por um componente é 40J por segundo. Quanto
tempo será necessário para que sejam dissipados 640J?
3) Quantos joules uma pequena lâmpada de 2W dissipa em 8h?
4) Durante quanto tempo um resistor deve ser percorrido por uma corrente
estacionária de 2A, a qual gera uma tensão de 3 V sobre o resistor, para que
ele dissipe uma quantidade de energia igual a 12J?
17
1.6 – FONTES DE ELETRICIDADE
Bateria:
 Uma bateria “bateria de células” consiste de uma combinação de
duas ou mais células similares;
 Uma célula é uma unidade fundamental de geração de energia
elétrica pela conversão de energia química ou solar;
 Todas as células podem ser classificadas como primária ou
secundária:
- Célula secundária: Recarregável (reação química reversível);
- Célula primária: Não pode ser recarregada.
 Os dois tipos mais comuns de baterias recarregáveis são:
- Bateria de chumbo-ácido: Usadas principalmente em automóveis;
- Bateria de níquel-cádmio: Usadas em calculadoras, ferramentas
portáteis, etc.
Exemplo: Bateria de carro.
Em geral possui 6 células.
2,1V
2,1V
2,1V
2,1V
2,1V
2,1V
_
+
_ +
_ + _ + _ + _ + _ +
12,6V
Metal
Eletrólito
+
18
1.7 - GERAÇÃO E FONTES DE CORRENTE ALTERNADA
Em geral, nossos sistemas de geração, transmissão e distribuição de energia
elétrica, dão-se por meio de tensões e correntes alternadas, ou seja, ondas
como funções senoidais ou cossenoidais.
Praticamente, existem vários dispositivos capazes de gerar tais ondas, mas
vamos aqui discutir a forma mais usual delas que é através da indução
eletromagnética, ou seja, através de máquinas rotativas, as “máquinas
síncronas”, máquina essa presente em todos os hidro e turbogeradores.
USINA HIDRELÉTRICA
19
USINA HIDRELÉTRICA
20
TIPOS DE TURBINAS
PELTON
21
TIPOS DE TURBINAS
FRANCIS
22
TIPOS DE TURBINAS
KAPLAN
23
OUTROS TIPOS DE GERAÇÃO
USINA A VAPOR
SOLAR
EÓLICA
24
Princípio da geração de tensões.
Considere uma espira imersa em um campo magnético constante e
uniforme, criado pelos pólos Norte e Sul.
S
A0 = Área da espira
A0

 = Velocidade angular
N
Sendo o fluxo constante e girando-se a espira com uma velocidade angular
 definida, resulta no movimento relativo entre a espira e o campo.
Desta forma, pela lei de Faraday- Lenz, nos terminais dessa espira será
induzida uma tensão, a qual poderá ser aplicada a um circuito externo
através de anéis coletores e escovas.
4
3
5
N 2
Posições instantâneas de
rotação à velocidade constante.
6 S
1
7
0
Fem nas posições
respectivas
0
0
45° 90° 135°
1
2
3
180° 225° 270° 315°
4
5
6
7
360°
8
25
Obs.:
A rotação da espira provoca uma variação contínua do fluxo magnético
que atravessa o condutor, induzindo assim uma tensão de onda senoidal no
condutor.
Esta variação do fluxo é a tensão induzida que varia de zero, quando o
condutor está na vertical e para um máximo, quando o condutor está na
horizontal.
Se t = 0s corresponde a um tempo quando o condutor está na vertical e a
tensão induzida está aumentando, a tensão induzida é:
v  Vm sen  t
Vm  é o valor de pico ou amplitude
sen  é o indicador de operação para uma onda sen oidal
Onde:
 t  é o arg umento
  é o símbolo de quantidade para a " freqüência radiana" ou
" velocidadea angular " ou " freqüência angular " da tensão.
  2 f
26
Ciclos de tensão alternada gerada pela rotação de uma espira
Posição 1
0
0
V
N
S
Posição 2
0 90°
90° V
N
S
Posição 3
0 90° 180°
V
N
S
180°
Posição 4
0 90° 180° 270°
V
270°
N
S
Posição 5
0 90° 180° 270° 360°
360°
V
N
S
27
REPRESENTAÇÃO DE FUNÇÕES SENOIDAIS
Seja a função senoidal:
v1  20 sen 377t V
  377rad / s
f 

 60 Hz
2
T
1
 16,7ms
60
v1 (V)
20
1,67 4,17
-20
8,33 10
12,5
16,7
0,628 1,57=/2  3,77 4,71=1,5 2
36° 90°
180° 216° 270°
360°
t (ms)
t (rad)
v2  20 sen( 377t  30)V
É a soma de dois termos ( o 1° está em radiano e
o 2° em graus ), os 30° chama-se ângulo de defasagem.
v2 (V)
20
10
1,67 4,17
8,33 10
12,5
16,7
t (ms)
-20
28
Onda co-senoidal (cos):
V3  20 sen( 377t  90)  20 cos 377t [V ]
Sua forma de onda tem o mesmo formato que a forma de onda senoidal,
mas é avançada de 90° (um quarto de período). Observe que os valores da
onda co-senoidal v3 ocorrem um quarto do período mais cedo do que a
onda senoidal v1.
v3 (V)
20
1,67 4,17
8,33 10
12,5
36°
180° 216° 270°
16,7
t (ms)
-20
90°
360°
29