Lista_Lancamentos_3a_serie

LISTA - LANÇAMENTOS – 3ª SÉRIE - TREINAMENTO
1. (Pucpr 2017) Num parque da cidade, uma criança lança uma bola verticalmente para
cima, percebendo a sua trajetória de subida e descida e, depois, recebe-a em suas mãos.
O lançamento dessa bola poderá ser representado pelo gráfico posição (y) versus tempo
(t), em que a origem dos eixos coincide com as mãos da criança.
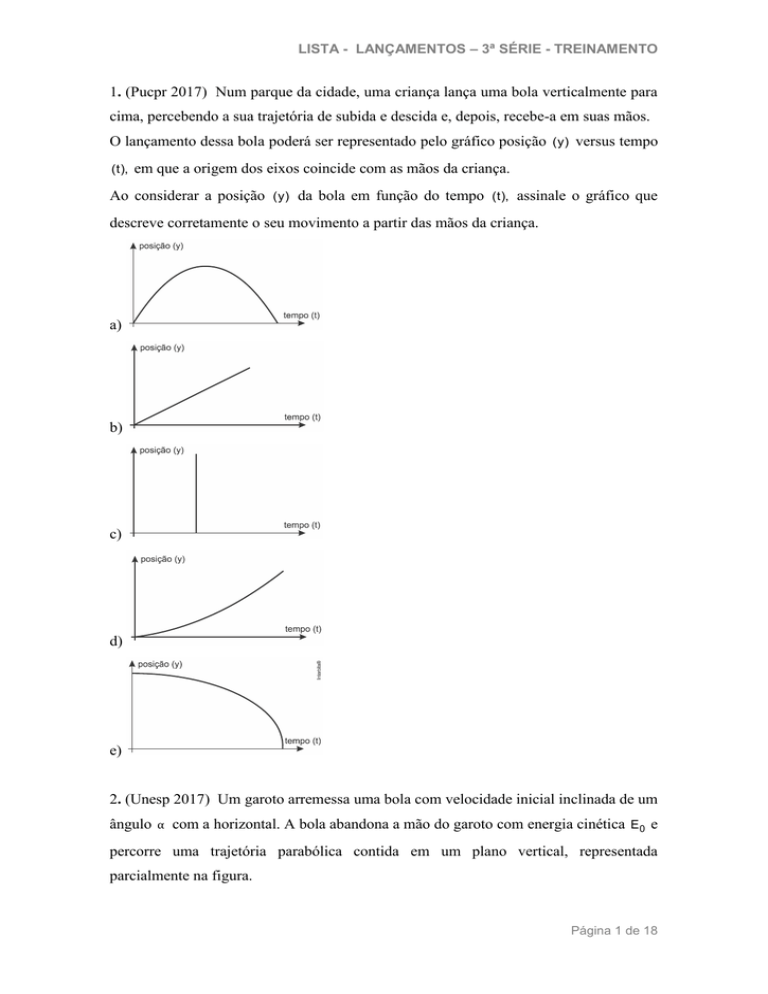
Ao considerar a posição (y) da bola em função do tempo (t), assinale o gráfico que
descreve corretamente o seu movimento a partir das mãos da criança.
a)
b)
c)
d)
e)
2. (Unesp 2017) Um garoto arremessa uma bola com velocidade inicial inclinada de um
ângulo α com a horizontal. A bola abandona a mão do garoto com energia cinética E0 e
percorre uma trajetória parabólica contida em um plano vertical, representada
parcialmente na figura.
Página 1 de 18
LISTA - LANÇAMENTOS – 3ª SÉRIE - TREINAMENTO
Desprezando-se a resistência do ar, a energia cinética da bola no ponto mais alto de sua
trajetória é
a) E0  sen α
b) E0  cos α
c) E0  cos2 α
d) E0  sen2 α
e)
E0  sen2 α
2
3. (G1 - ifce 2016) A velocidade horizontal mínima necessária para uma pessoa pular
do ponto X e atingir o ponto Y, como mostra a figura abaixo, deve ser de
(Despreze a resistência do ar e considere a aceleração da gravidade como sendo
g  10 m s2 )
a) 1m s.
b) 5 m s.
c) 4 m s.
Página 2 de 18
LISTA - LANÇAMENTOS – 3ª SÉRIE - TREINAMENTO
d) 8 m s.
e) 9 m s.
4. (G1 - cftmg 2016) Um objeto é lançado para baixo, na vertical, do alto de um prédio
de 15 m de altura em relação ao solo. Desprezando-se a resistência do ar e sabendo-se
que ele chega ao solo com uma velocidade de 20 m / s, a velocidade de lançamento, em
m / s, é dada por
a) 10.
b) 15.
c) 20.
d) 25.
5. (G1 - ifsc 2016) Joana, uma dedicada agricultora, colocou várias laranjas sobre uma
mesa cuja altura é 0,80 m. Considerando que uma dessas laranjas caiu em queda livre,
isto é, sem a interferência do ar, assinale a alternativa CORRETA.
a) A laranja caiu com energia cinética constante.
b) A laranja caiu com velocidade constante.
c) A laranja caiu com aceleração constante.
d) A laranja caiu com energia potencial constante.
e) O movimento da laranja foi retilíneo e uniforme.
6. (G1 - ifba 2016) Um garoto, treinando arremesso de pedras com uma atiradeira, gira
o dispositivo de 0,80 m de comprimento sobre sua cabeça, descrevendo um movimento
circular com velocidade constante e aceleração radial de 370,00 m s2 , conforme
diagrama. Num certo instante de tempo, a pedra é lançada tangencialmente à trajetória e
atinge o solo numa posição de 10,00 m em relação ao garoto. Considere desprezível a
resistência do ar e g  10,00 m s2 . Assim, podemos afirmar que a altura do garoto, em
metros, é, aproximadamente, igual a:
Página 3 de 18
LISTA - LANÇAMENTOS – 3ª SÉRIE - TREINAMENTO
a) 1,50
b) 1,58
c) 1,69
d) 1,81
e) 1,92
7. (G1 - ifce 2016) Considere a figura abaixo, na qual Michele utiliza uma bola de tênis
para brincar com seu cãozinho, Nonô.
Nesta situação, Michele arremessa a bola na direção horizontal para que Nonô corra em
sua direção e a pegue. Ao ser arremessada, a bola sai da mão de Michele a uma
velocidade de 14,4 km h e uma altura de 1,80 m do chão. Nesse instante, Nonô encontrase junto aos pés de sua dona.
Dadas estas condições, o tempo máximo que Nonô terá para pegar a bola, antes que a
mesma toque o chão pela primeira vez, é
(Despreze o atrito da bola com o ar e considere a aceleração da gravidade com o valor
g  10 m s2 .)
Página 4 de 18
LISTA - LANÇAMENTOS – 3ª SÉRIE - TREINAMENTO
a) 0,375 s.
b) 0,6 s.
c) 0,75 s.
d) 0,25 s.
e) 1,0 s.
8. (Fmp 2016) Um jogador de futebol chuta uma bola sem provocar nela qualquer
efeito de rotação. A resistência do ar é praticamente desprezível, e a trajetória da bola é
uma parábola. Traça-se um sistema de eixos coordenados, com um eixo x horizontal e
paralelo ao chão do campo de futebol, e um eixo y vertical com sentido positivo para
cima.
Na Figura a seguir, o vetor v0 indica a velocidade com que a bola é lançada (velocidade
inicial logo após o chute).
Abaixo estão indicados quatro vetores w1, w2, w 3 e w4 , sendo w 4 o vetor nulo.
Página 5 de 18
LISTA - LANÇAMENTOS – 3ª SÉRIE - TREINAMENTO
Os vetores que descrevem adequada e respectivamente a velocidade e a aceleração da
bola no ponto mais alto de sua trajetória são
a) w1 e w 4
b) w 4 e w 4
c) w1 e w 3
d) w1 e w 2
e) w 4 e w 3
9. (Pucpr 2016) Durante um jogo de futebol, um goleiro chuta uma bola fazendo um
ângulo de 30 com relação ao solo horizontal. Durante a trajetória, a bola alcança uma
altura máxima de 5,0 m. Considerando que o ar não interfere no movimento da bola,
qual a velocidade que a bola adquiriu logo após sair do contato do pé do goleiro?
Use g  10 m s2 .
Página 6 de 18
LISTA - LANÇAMENTOS – 3ª SÉRIE - TREINAMENTO
a) 5 m s.
b) 10 m s.
c) 20 m s.
d) 25 m s.
e) 50 m s.
TEXTO PARA A PRÓXIMA QUESTÃO:
Se necessário, use
aceleração da gravidade: g  10 m / s2
densidade da água: d  1,0 kg / L
calor específico da água: c  1cal / g C
1cal  4 J
constante eletrostática: k  9 ,0  109 N  m2 / C2
constante universal dos gases perfeitos: R  8 J / mol  K
10. (Epcar (Afa) 2016) Uma partícula de massa m e carga elétrica q é lançada com
um ângulo θ em relação ao eixo x, com velocidade igual a v 0 , numa região onde
atuam um campo elétrico E e um campo gravitacional g, ambos uniformes e
constantes, conforme indicado na figura abaixo.
Página 7 de 18
LISTA - LANÇAMENTOS – 3ª SÉRIE - TREINAMENTO
Desprezando interações de quaisquer outras naturezas com essa partícula, o gráfico que
melhor representa a variação de sua energia potencial ( Ep ) em função da distância (d)
percorrida na direção do eixo x, é
a)
b)
c)
d)
11. (Mackenzie 2015) Vários corpos idênticos são abandonados de uma altura de
7,20m em relação ao solo, em intervalos de tempos iguais. Quando o primeiro corpo
atingir o solo, o quinto corpo inicia seu movimento de queda livre. Desprezando a
Página 8 de 18
LISTA - LANÇAMENTOS – 3ª SÉRIE - TREINAMENTO
resistência do ar e adotando a aceleração da gravidade g  10,0 m / s2, a velocidade do
segundo corpo nessas condições é
a) 10,0 m / s
b) 6,0 m / s
c) 3,0 m / s
d) 9,0 m / s
e) 12,0 m / s
12. (Uerj 2015) Uma ave marinha costuma mergulhar de uma altura de 20 m para
buscar alimento no mar.
Suponha que um desses mergulhos tenha sido feito em sentido vertical, a partir do
repouso e exclusivamente sob ação da força da gravidade.
Desprezando-se as forças de atrito e de resistência do ar, a ave chegará à superfície do
mar a uma velocidade, em m/s, aproximadamente igual a:
a) 20
b) 40
c) 60
d) 80
13. (Pucmg 2015) O edifício mais alto do Brasil ainda é o Mirante do Vale com 51
andares e uma altura de 170 metros. Se gotas de água caíssem em queda livre do último
andar desse edifício, elas chegariam ao solo com uma velocidade de aproximadamente
200 km / h e poderiam causar danos a objetos e pessoas. Por outro lado, gotas de chuva
caem de alturas muito maiores e atingem o solo sem ferir as pessoas ou danificar
objetos. Isso ocorre porque:
a) quando caem das nuvens, as gotas de água se dividem em partículas de massas
desprezíveis.
b) embora atinjam o solo com velocidades muito altas, as gotas não causam danos por
serem líquidas.
c) as gotas de água chegam ao solo com baixas velocidades, pois não caem em queda
livre devido ao atrito com o ar.
d) as gotas de água têm massas muito pequenas e a aceleração da gravidade
praticamente não afeta seus movimentos verticais.
Página 9 de 18
LISTA - LANÇAMENTOS – 3ª SÉRIE - TREINAMENTO
14. (Ifsul 2015) Um corpo A é abandonado de um ponto situado a 10 metros acima do
solo. No mesmo instante, um corpo B é lançado verticalmente de baixo para cima com
velocidade v 0 suficiente para que possa atingir 10 metros de altura.
Desprezando a resistência do ar, chamando respectivamente v A e vB as velocidades de
A e B quando se encontram a 5 metros de altura, o valor da razão v A vB , em módulo
é
a) 4
b) 2
c) 1
d) 1 2
15. (Mackenzie 2015) Dois corpos A e B de massas mA  1,0 kg e mB  1,0  103 kg,
respectivamente, são abandonados de uma mesma altura h, no interior de um tubo
vertical onde existe o vácuo. Para percorrer a altura h,
a) o tempo de queda do corpo A é igual que o do corpo B.
b) o tempo de queda do corpo A é maior que o do corpo B.
c) o tempo de queda do corpo A é menor que o do corpo B.
d) o tempo de queda depende do volume dos corpos A e B.
e) o tempo de queda depende da forma geométrica dos corpos A e B.
Página 10 de 18
LISTA - LANÇAMENTOS – 3ª SÉRIE - TREINAMENTO
Gabarito:
Resposta da questão 1: [A]
A posição em função do tempo de um objeto em lançamento vertical varia
quadraticamente, indicando o gráfico de uma parábola, sendo o movimento de subida
retardado e a descida acelerado. O movimento é retilíneo uniformemente retardado na
subida até a altura máxima atingida pelo objeto e a descida passa a ser acelerada sendo
em ambos os trechos a aceleração igual à da gravidade.
Resposta da questão 2: [C]
A energia cinética ao abandonar a mão do garoto é: E0 
m v 02
.
2
(I)
No ponto mais alto da trajetória a velocidade é: v x  v0 cos α.
m v 02
m v 2x m  v 0 cos α 


 cos2 α.
2
2
2
2
A energia cinética nesse ponto mais alto é: E 
Substituindo (I) em (II):
(II)
E  E0  cos2 α.
Resposta da questão 3: [B]
Para sabermos qual a velocidade mínima que ele deve exercer para realizar o salto,
primeiro precisamos saber quanto tempo que ele vai demorar pra descer em queda livre.
ΔS  V0y  Δt 
1
 a  Δt 2
2
1
 a  Δt 2
2
2ΔS
2  1,8
t
 t  0,6 s
a
10
ΔS  0 
t
Descobrimos que ele demora 0,6 s pra cair, logo ele deverá percorrer 3 m em 0,6 s. A
velocidade inicial que ele deve exercer será:
Página 11 de 18
LISTA - LANÇAMENTOS – 3ª SÉRIE - TREINAMENTO
ΔS  V0x  Δt  V0x 
ΔS
3
 V0x 
 V0x  5 m s
Δt
0,6
Vale lembrar que a velocidade no eixo y sempre será um M.R.U.V. e a velocidade e no
eixo x sempre será um M.R.U.
Resposta da questão 4: [A]
Dado: v  20m s; h  15m; g  10 m s2.
Aplicando a equação de Torricelli:
v 2  v 02  2gh  v 0 
v 2  2gh 
202  2  10  15 
100 
v 0  10 m s.
Resposta da questão 5: [C]
A laranja caiu com aceleração constante, igual à aceleração da gravidade.
Resposta da questão 6: [C]
Primeiramente, calcula-se a velocidade horizontal da pedra no instante do lançamento,
usando-se a expressão da aceleração centrípeta (radial) do movimento circular
uniforme:
ac 
v2
 v  R  ac  v  0,80 m  370 m / s2  v  17,2 m / s
R
Essa velocidade horizontal é constante, pois não há atrito, portanto podemos calcular o
tempo para a pedra se deslocar 10m na horizontal, sendo este tempo o mesmo para a
pedra cair da altura h.
Δt 
Δx
10 m
 Δt 
 Δt  0,58 s
v
17,2 m / s
Página 12 de 18
LISTA - LANÇAMENTOS – 3ª SÉRIE - TREINAMENTO
Usando a equação da altura em função do tempo para o movimento de queda livre na
direção vertical, temos:
0,58 s
t2
 h  10 m / s2 
 h  1,69 m
2
2
2
h  g
Resposta da questão 7: [B]
No lançamento horizontal, o tempo de queda independe da velocidade inicial, sendo
igual ao tempo de queda livre. Assim:
h
g 2
t
 t
2
2h

g
2  1,8

10
t  0,6s.
Resposta da questão 8: [D]
No lançamento oblíquo com ausência de atrito com o ar, podemos dividir o movimento
nos eixos vertical e horizontal, usando as componentes da velocidade nestes eixos
 v x e v y , conforme a figura abaixo:
Assim, temos no eixo vertical um movimento de lançamento vertical em que a
aceleração é dada pela gravidade local e no eixo horizontal um movimento retilíneo
uniforme em que a velocidade em x é sempre constante.
Observa-se que no ponto mais alto da trajetória a velocidade em y é nula e a velocidade
horizontal representa a velocidade da bola neste ponto, enquanto que a aceleração é a
mesma em todos os pontos do movimento, sendo constante e apontando para baixo.
Logo, a alternativa correta é letra [D].
Página 13 de 18
LISTA - LANÇAMENTOS – 3ª SÉRIE - TREINAMENTO
Resposta da questão 9: [C]
Sabendo que na posição da altura máxima a componente vertical da velocidade é zero,
utilizando a equação de Torricelli, podemos dizer que:
v y 2  v oy 2  2  a  ΔS
0  v oy 2  2  g  Hmáx
v oy 2  2  10  5
v oy  100
v oy  10 m s
Note que a aceleração neste movimento é em módulo igual a aceleração da gravidade.
Porém, a  g, devido a aceleração da gravidade, no movimento analisado, está contra o
movimento.
Sabendo que o ângulo de lançamento da bola é de 30C, podemos encontrar a
velocidade inicial da bola.
v oy  v o  sen  30 
vo 
v oy
sen  30 

10
12
v o  20 m s
Resposta da questão 10: [B]
Neste questão, temos uma composição de movimentos, pois se trata de um lançamento
oblíquo em que devido ao campo elétrico surge uma força elétrica de mesma direção e
sentido da força gravitacional atuando na vertical para baixo. Assim, temos uma
aceleração resultante obtida pela soma da aceleração da gravidade com a aceleração
elétrica que aponta no mesmo sentido que a força elétrica, cujo módulo é:
a  g
qE
m
Página 14 de 18
LISTA - LANÇAMENTOS – 3ª SÉRIE - TREINAMENTO
O movimento da partícula representa uma parábola com a concavidade voltada para
baixo, mas precisamos de uma função que relacione a variação da energia potencial
gravitacional com o eixo x.
Decompondo a velocidade inicial v 0 nos eixos x e y:
v0x  v0  cosθ
v0y  v0  sen θ
Para o eixo x, temos um MRU, sendo a equação dada por:
x  x0  v0x t  x  v0  t cosθ
Isolando t:
t
x
(1)
v 0  cosθ
Para o eixo y, temos um MRUV, sendo a equação da posição vertical com o tempo dada
por:
a
y  y0  v0y t  t 2
2
Δy  v 0  sen θ  t 
a 2
t (2)
2
Substituindo a equação (1) na equação (2):
Δy  t g θ  x 
a
x2
(3)
2 v02  cos2 θ
E, como a variação da energia potencial gravitacional é dada por:
ΔEp  m  g  Δy
Substituindo Δy finalmente ficamos com:


a
x2

ΔEp  m  g   t g θ  x 

2 v 02  cos2 θ 

Página 15 de 18
LISTA - LANÇAMENTOS – 3ª SÉRIE - TREINAMENTO
Logo, temos uma equação representativa de uma parábola cuja concavidade está voltada
para baixo. Alternativa [B].
Resposta da questão 11: [D]
Calculando o tempo de queda:
h
1 2
g t q  tq 
2
2h

g
2  7,2 
10
 1,44  t q  1,2 s.
A figura mostra os cinco corpos e o tempo (t) de movimento de cada um deles.
A velocidade do 2º corpo é:
v  v 0  g t  v  0  10  0,9  
v  9 m/s.
Resposta da questão 12: [A]
Usando a equação de Torricelli com a = g = 10 m/s2 e ΔS  h  20m.
v 2  v 02  2g h  v 2  0  2  10  20  400 
v  20 m/s.
Resposta da questão 13: [C]
Página 16 de 18
LISTA - LANÇAMENTOS – 3ª SÉRIE - TREINAMENTO
A queda da gota é, no início, um movimento acelerado. À medida que ela vai caindo, a
força de resistência do ar vai aumentando com a velocidade até atingir a mesma
intensidade do seu peso. Nesse ponto, a gota atinge sua velocidade limite, terminando a
queda em movimento uniforme, com velocidade em torno de 30 km/h, insuficiente para
causar danos a objetos ou pessoas.
Resposta da questão 14: [C]
Temos situações semelhantes para os dois corpos, pois ambos percorrem 5 m com as
mesmas acelerações sendo que as condições de contorno também são similares, logo as
velocidades em módulo serão iguais e sua razão será 1.
Outra possibilidade é calcular usando os conhecimentos de lançamento vertical e queda
livre.
Para o corpo A, que cai em queda livre, usando o referencial positivo para baixo e a
equação de Torricelli:
v 2  v02  2gΔh  v  v02  2gΔh
v A  02  2  10  5  v  10 m / s
Para o corpo B, que sobe na vertical, usando o referencial positivo para cima,
primeiramente descobrimos a velocidade inicial e depois a velocidade na posição de
5m:
v2  v02  2gΔh  v0  v2  2gΔh
v0  02  2  10  10  v0  10 2 m s
E a intensidade da velocidade a 5 m de altura:
vB 
10 2 
2
 2  10  5  v  10 m / s
Página 17 de 18
LISTA - LANÇAMENTOS – 3ª SÉRIE - TREINAMENTO
Então,
v A 10

 1.
vB 10
Resposta da questão 15: [A]
Se o corpo está em queda livre, a resultante das forças sobre ele é seu próprio peso.
Aplicando a segunda lei de Newton a essa situação:
R  P  m a  m g  a  g.
A aceleração de queda independe da massa e é igual a aceleração da gravidade.
Calculando o tempo de queda:
h
g 2
t  t
2
2h
.
g
Consequentemente, o tempo de queda também independe da massa. Portanto, o tempo
de queda é o mesmo para os dois corpos.
Página 18 de 18