Capacitores

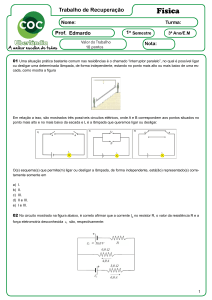
Aula 4_1
Capacitores
Física Geral e Experimental III
Prof. Cláudio Graça
Capítulo 4
Capacitores
• Definição da Capacitância: capacitor e sua
capacitância
• Carga de um capacitor
• Exemplos de Cálculo da Capacitância
• (1) Capacitor de Placas Paralelas
Diferentes formas
• (2) Capacitor Cilíndrico
de capacitores
• (3) Capacitor esférico
Aplicação!
• (4) Esfera Isolada
• Dimensões da capacitância
Capacitores
Capacitores
Capacitores
de grandes
dimensões
O que é capacitor?
„
„
„
É um componente que
armazena carga elétrica.
Normalmente, está
presente em todos
componentes, mas é uma
propriedade fundamental
dos capacitores.
O capacitor básico tem
duas placas planas
isoladas com um
dielétrico .
Geometria dos capacitores
Placas
condutoras
Insulante
(dielétrico)
Circuitos elementares
Os circuitos elementares são constítuidos de elementos com funções independentes
cujas propriedades elétricas na Física III, são estudadas como resistivas,
capacitivas e indutivas....outros elementos como os diodos tríodos etc..podem ser
entendidos a partir dos primeiros.
Exemplo de um Circuito
ε
C
R
O que é um capacitor?
•
É um dispositivo que armazene carga de forma eficiente, obedecendo à
relação, chamada capacitância:
Q
C=
V
•
•
Portanto: Capacitor é um dispositivo e capacitância é uma
propriedade
Outros nomes: condensador, capacitor e tanque
O que é um capacitor?
Capacitância
Q
C=
V
Unidade: F = C/V (Farad)
Qualquer corpo que armazene carga independente
da sua função possui uma capacitância!
Exemplos:
Capacitores
Resistores
Indutores
Condutores
Diodos
Tríodos
Linhas de transmissão
Transformadores
Etc.
Carga de um capacitor
S
V
R
++++
---- C
• Fechando S se aplica V em C, (não imediatamente) e os e-s
movem-se do terminal -V para a placa inferior, induzindo
carga positiva na placa superior
• A resistência R limita a corrente e a capacitância a carga total
portanto: O tempo característico do processo de carga do
capacitor, depende do produto RC, cuja unidade é s.
Carga do Capacitor
+
+
+
_
_
-
Carregando um capacitor...
VC<V
++ ++
-- --
• Enquanto V > Vc , os e-s movem-se
para o capacitor e a carga positiva
é induzida...
C é a capacitância em Farad (F)
VC=V
++++++
---------
Quando V = Vc , C atinge a carga
plena
•
Qualquer Carga sempre ∝ V
Q = CV
CÁLCULO DA CAPACITÂNCIA
-Q
+Q
A
++++
d- - - - -
+Q
-Q
a
b
L
b
• Um capacitor é um dispositivo formado por
dois condutores separados e carregados
com uma carga +Q e –Q respectivamente.
+Q -Q
a
• A capacitância é definida como sendo a
relação entre o valor da carga em uma
das placas e a diferença de potencial
entre as duas placas.
a
b
C
C≡
Q
ΔV
Capacitor de placas planas
•
Calcule a capacitância, considerando
que a densidade de carga das placas
vale +σ e - σ respectivamente. A área
das placas é A e a distância entre as
mesmas é d, mantida uma diferença de
potencial V.
C≡
• Definição:
• Dados:
• Cálculo:
A, d, σ
A
++++
d -----
Q
ΔV
r r
Q = σA; ΔV = − ∫ E ⋅ d l
d
0
• Aplicando a Lei de Gauss calcula-se o campo elétrico
e a seguir a diferença de potencial.
Capacitor de placas planas
Para aplicar a Lei de Gauss envolve-se
uma das placas com uma gaussiana,
como mostra a figura.
r r
Q σA
Φ E = ∫ E ⋅ dA = EA = =
εo
A
∴ E=
εo
σ
Q
=
ε 0 Aε 0
r r
Q
VB − VA = − ∫ E ⋅ d l =
d
Aε 0
A
B
⇒
• A capacitância depende unicamente das
dimensões do capacitor (A,d).
Q Aε 0
C≡ =
V d
Capacitor Cilíndrico
•
Calcular a capacitância
•
Considere as cargas +Q, e -Q
nas superfícies cilíndricas,
cuja diferença de potencial é
V.
r
a
b
L
Dados: raio interno = a
raio externo = b
comprimento = L
Mesma metodologia:
calcular o campo elétrico,
integrar para obter a
diferença de potencial e
obter o valor da carga
E
Lei de Gauss
ΔV
r r
∫ E ⋅ dS
Q
Q = ∫ σdA
Cálculo de E para simetria cilíndrica
• A superfície Gaussiana é
cilíndrica com raio r e
comprimento L
Er
Er
• O cilindro possui carga Q
+Q+ +
• Aplicando
r arLei de Gauss:
++++
L
ΦE = ∫ E ⋅ dA = ∫ EdAcos0
= E∫ dA = E2π rL =
Q
ε0
⇒
E=
Q
2πε0 Lr
Capacitor Cilíndrico
• Cálculo da capacitância
r
o campo elétrico será:
+σ
Q
E=
2 πε 0 rL
-σ
a
b
L
Considerando que a placa interna possui uma carga +Q e
potencial V e o potencial da placa externa é nulo em r = b:
a
b
r
r
V = − ∫ E • d l = − ∫ Edr = ∫
a
b
b
⇒
C≡
Q
b
Q
dr =
ln⎛⎜ ⎞⎟
2 πε 0 L ⎝ a ⎠
a 2 πε 0 rL
Q 2 πε 0 L
=
V ln⎛ b ⎞
⎜ ⎟
⎝ a⎠
Novamente: depende
só da geometria (a,b,L).
Capacitor Esférico
• O capacitor esférico é formado por
duas cascas esféricas de raios a e b,
respectivamente, com carga +Q e -Q.
-Q
+Q
• O cálculo da capacitância segue a mesma
lógica anterior, iniciando com a aplicação
da Lei de Gauss, para obter o campo
elétrico entre as placas:
Q
E=
4πεo r 2
b
Gaussiana
b
b
Q b dr
Q ⎡ 1⎤
Q ⎛ 1 1⎞
V = ∫ E ( r )dr =
=
−
=
⎜ − ⎟
∫ 2
⎢
⎥
4 πε 0 a r
4 πε 0 ⎣ r ⎦ a 4 πε 0 ⎝ a b ⎠
a
C≡
a
4πε0
Q
ab
= 4πε0
=
V ⎛1 1⎞
b−a
⎜ − ⎟
⎝a b⎠
Esfera Isolada
•
Uma esfera metálica, isolada pode
ser considerada a partir de um
capacitor cuja placa externa é levada
ao infinito !
C≡
•
4πεo
Q
=
ΔV ⎛ 1 1 ⎞
⎜ − ⎟
⎝a b⎠
+
+
+
para b → ∞ ⇒ C = 4πεo a
Para uma esfera de raio genérico r
C = 4πεo r
+r
Curiosidade
• Capacidade de uma esfera da dimensão da terra:
R ~6000 km=6x106 m.
• C = 4πεoR = 4πx8,852x10-12 x6x106 = 0,67 mF
• Comparando com um capacitor de placas planas, de mesma
capacitância, cuja distância entre as placas fosse de 0,1 mm
(uma folha de papel):
C = (Aε0 ) / d = (A * 8.852x10-12 Fm -1) / 0.0001 m
= 0,67x10-3 F
A=7569 m2 = 87m x 87m (quase uma quadra!)
Dimensões da capacitância
• C = Q/V => [C] = Farad
• Exemplo: A = 10cm2
d = 0,01cm (uma folha de papel)
=> C = Aε0/d = 0.01m2/0.0001m * 8.852x10-12 C2/Jm
= 8.852x10-10 F=0,8852nF
F (farad)
mF
10-3
μF
10-6
nF
10-9
pF
10-12
Capacitor de placas enroladas
Aplicação dos capacitores
Capacitores variáveis
„
„
„
Capacitores variáveis
são usados em rádios,
televisores VCRs etc.
A capacitância é
ajustada pelo usuário
Trimmers são
capacitores de ajuste
interno para a
calibração de
sistemas por técnicos.